新人教版数学学七年级下 8.2 消元—二元一次方程组的解法
文档属性
| 名称 | 新人教版数学学七年级下 8.2 消元—二元一次方程组的解法 |

|
|
| 格式 | zip | ||
| 文件大小 | 32.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-17 20:43:58 | ||
图片预览






文档简介
(共16张PPT)
§8.2 用“加减消元法”解
二元一次方程组
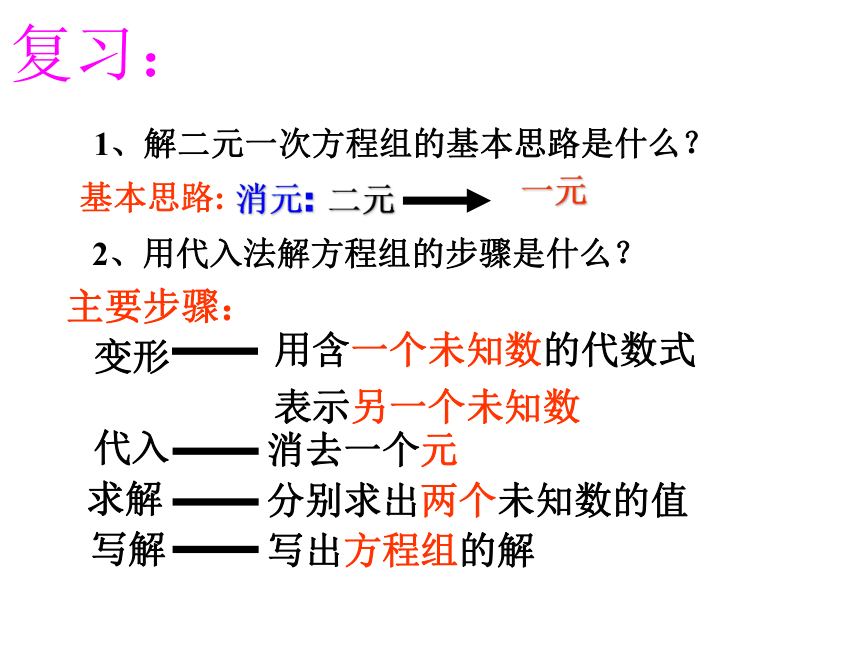
主要步骤:
基本思路:
写解
求解
代入
一元
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程组的步骤是什么?
一元
复习:
练习2:用代入消元法解方程组
X+y=7
2x-y=2
①
②
{
解二元一次方程组的基本思想 —— ( )
消 元
大家想一想:除了用代入法之外,还有没有其他的方法来消元呢
练习1:已知x+y=7,用含x的代数式表示y,则y=_____ ;
用含y的代数式表示x,则x=__________ .
课前热身:
合并同类项
(1) 3x+(-3x) =_____
(2) 2y-2y=______
(3) 9x+_____=0
(4) 7y-_____=0
想一想:在一个方程组里,如果某个未知数的系数是相同或互为相反数,我们可不可以用加减法消去这个未知数。
0
0
(-9x)
7y
做一做:
X + y = 7
2 x – y = 2
①
②
{
解:
①
②
+
得
3 x = 9
∴ X = 3
把X=3代入①,得
3+y=7
∴ y=4
∴{
X=3
y=4
解方程组
探究学习:
观察:未知数y的系数有什么关系?除了代入法还有其它方法吗?
注意到这个方程组中,未知数y的系数互为相反数,.请你把这两个方程的左边与左边相加,右边与右边相加,看看,能得到什么结果?.
探 索:
把两个方程的两边分别相加,就消去了y,得到3x=9
X=3.
①
②
解:
①
②
-
得
9y = -18
∴ y = -2
把y=-2代入①,得
3x-10=5
∴ x=5
∴{
X=5
y=-2
解方程组
探究学习:
观察:未知数x的系数有什么关系?你有何想法吗?
注意到这个方程组中,未知数x的系数相同,都是3.请你把这两个方程的左边与左边相减,右边与右边相减,看看,能得到什么结果?
探 索:
把两个方程的两边分别相减,就消去了x,得到9y=-18.
y=-2.
通过将两个方程相加(或相减)消去一个未知数,将方程组转化为一元一次方程来解的.这种解法叫做加减消元法,简称加减法.
思 考:
从上面的解答过程中,你发现了二元一次方程组的新解法吗?
利用加减消元法解方程组时,在方程组的两个方程中:
(1)某个未知数的系数互为相反数,则可以直接
消去这个未知数;
(2)如果某个未知数系数相等,则可以直接
消去这个未知数
把这两个方程中的两边分别相加。
把这两个方程中的两边分别相减,
你来说说:
解下列方程组:
1. 2.
3. 4.
初步尝试:
{
3x - 4y = 10
5x + 6y = 42
①
②
解方程组:
分析:利用等式的基本性质将某个未知数的系数变为相同或互为相反数,即可用加减法消去这个未知数。
∴{
解:
①×3,
②×2
得
19 x = 114
∴ X = 6
把X=6代入②,得
30+6y=42
∴ y=2
X=6
y=2
6y=12
{
9x- 12y = 30
10x+12y=84
③
④
③+④,得
例题讲解
X的系数是3和5既不相等,也不互为相反数,y的系数是-4和6也是既不相等,又不互为相反数。你有办法把其中一个未知数的系数变成相等或互为相反数吗?
探 索:
思 考:能否先消去x再求解?
在本节例2解方程组
时,用了什么方法?现在你会不会用加减法来解?试试看,并比较一下哪种方法更方便?
试一试:
解下列方程组:
1. 2.
3. 4.
初步尝试:
加减法解二元一次方程组的一般步骤:
4。写出方程组的解。
1。把一个方程(或两个方程)的两边都乘以一个适当的数,使两个方程的一个未知数的系数的绝对值相等;
2。把一个未知数系数绝对值相等的两个方程的两边分别相加(或相减),得到一个一元一次方程,求得一个未知数的值;
3。把这个未知数的值代入原方程组的任何一个方程,求得另一个未知数的值;
你来说说:
今天你收获了什么?
加减法解二元一次方程组
加减法解二元一次方程组的一般步骤:
1、有一个未知数的系数相等或互为相反数。
2、两个未知数的系数都不相等或都不互为相反数。
OK
知识拓展:
(1) 不解方程组
2X + 7y = 3
3x – 2y = 17
①
②
{
则 x + y = _______
已知:a-b=3,b-c=4,则 6(a-c)+8=_______
(3)关于x、y的方程组
{
3x + 2y = m
X – y = 4-m
的解满足2x+3y=3.
求m的值。
①
②
4
50
M=7/2
能力提高:
解方程组
﹛
2x+3y
4
+
2x-3y
3
= 7
2x+3y
3
+
2x-3y
2
= 8
①
②
你会用简便方法解这个方程组吗?
§8.2 用“加减消元法”解
二元一次方程组
主要步骤:
基本思路:
写解
求解
代入
一元
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程组的步骤是什么?
一元
复习:
练习2:用代入消元法解方程组
X+y=7
2x-y=2
①
②
{
解二元一次方程组的基本思想 —— ( )
消 元
大家想一想:除了用代入法之外,还有没有其他的方法来消元呢
练习1:已知x+y=7,用含x的代数式表示y,则y=_____ ;
用含y的代数式表示x,则x=__________ .
课前热身:
合并同类项
(1) 3x+(-3x) =_____
(2) 2y-2y=______
(3) 9x+_____=0
(4) 7y-_____=0
想一想:在一个方程组里,如果某个未知数的系数是相同或互为相反数,我们可不可以用加减法消去这个未知数。
0
0
(-9x)
7y
做一做:
X + y = 7
2 x – y = 2
①
②
{
解:
①
②
+
得
3 x = 9
∴ X = 3
把X=3代入①,得
3+y=7
∴ y=4
∴{
X=3
y=4
解方程组
探究学习:
观察:未知数y的系数有什么关系?除了代入法还有其它方法吗?
注意到这个方程组中,未知数y的系数互为相反数,.请你把这两个方程的左边与左边相加,右边与右边相加,看看,能得到什么结果?.
探 索:
把两个方程的两边分别相加,就消去了y,得到3x=9
X=3.
①
②
解:
①
②
-
得
9y = -18
∴ y = -2
把y=-2代入①,得
3x-10=5
∴ x=5
∴{
X=5
y=-2
解方程组
探究学习:
观察:未知数x的系数有什么关系?你有何想法吗?
注意到这个方程组中,未知数x的系数相同,都是3.请你把这两个方程的左边与左边相减,右边与右边相减,看看,能得到什么结果?
探 索:
把两个方程的两边分别相减,就消去了x,得到9y=-18.
y=-2.
通过将两个方程相加(或相减)消去一个未知数,将方程组转化为一元一次方程来解的.这种解法叫做加减消元法,简称加减法.
思 考:
从上面的解答过程中,你发现了二元一次方程组的新解法吗?
利用加减消元法解方程组时,在方程组的两个方程中:
(1)某个未知数的系数互为相反数,则可以直接
消去这个未知数;
(2)如果某个未知数系数相等,则可以直接
消去这个未知数
把这两个方程中的两边分别相加。
把这两个方程中的两边分别相减,
你来说说:
解下列方程组:
1. 2.
3. 4.
初步尝试:
{
3x - 4y = 10
5x + 6y = 42
①
②
解方程组:
分析:利用等式的基本性质将某个未知数的系数变为相同或互为相反数,即可用加减法消去这个未知数。
∴{
解:
①×3,
②×2
得
19 x = 114
∴ X = 6
把X=6代入②,得
30+6y=42
∴ y=2
X=6
y=2
6y=12
{
9x- 12y = 30
10x+12y=84
③
④
③+④,得
例题讲解
X的系数是3和5既不相等,也不互为相反数,y的系数是-4和6也是既不相等,又不互为相反数。你有办法把其中一个未知数的系数变成相等或互为相反数吗?
探 索:
思 考:能否先消去x再求解?
在本节例2解方程组
时,用了什么方法?现在你会不会用加减法来解?试试看,并比较一下哪种方法更方便?
试一试:
解下列方程组:
1. 2.
3. 4.
初步尝试:
加减法解二元一次方程组的一般步骤:
4。写出方程组的解。
1。把一个方程(或两个方程)的两边都乘以一个适当的数,使两个方程的一个未知数的系数的绝对值相等;
2。把一个未知数系数绝对值相等的两个方程的两边分别相加(或相减),得到一个一元一次方程,求得一个未知数的值;
3。把这个未知数的值代入原方程组的任何一个方程,求得另一个未知数的值;
你来说说:
今天你收获了什么?
加减法解二元一次方程组
加减法解二元一次方程组的一般步骤:
1、有一个未知数的系数相等或互为相反数。
2、两个未知数的系数都不相等或都不互为相反数。
OK
知识拓展:
(1) 不解方程组
2X + 7y = 3
3x – 2y = 17
①
②
{
则 x + y = _______
已知:a-b=3,b-c=4,则 6(a-c)+8=_______
(3)关于x、y的方程组
{
3x + 2y = m
X – y = 4-m
的解满足2x+3y=3.
求m的值。
①
②
4
50
M=7/2
能力提高:
解方程组
﹛
2x+3y
4
+
2x-3y
3
= 7
2x+3y
3
+
2x-3y
2
= 8
①
②
你会用简便方法解这个方程组吗?
