新人教版数学八年级下 19.2.1 矩形的定义和性质
文档属性
| 名称 | 新人教版数学八年级下 19.2.1 矩形的定义和性质 |  | |
| 格式 | zip | ||
| 文件大小 | 641.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-17 20:54:34 | ||
图片预览


文档简介
(共18张PPT)
19.2.1 特殊的平行四边形
----矩形的定义和性质
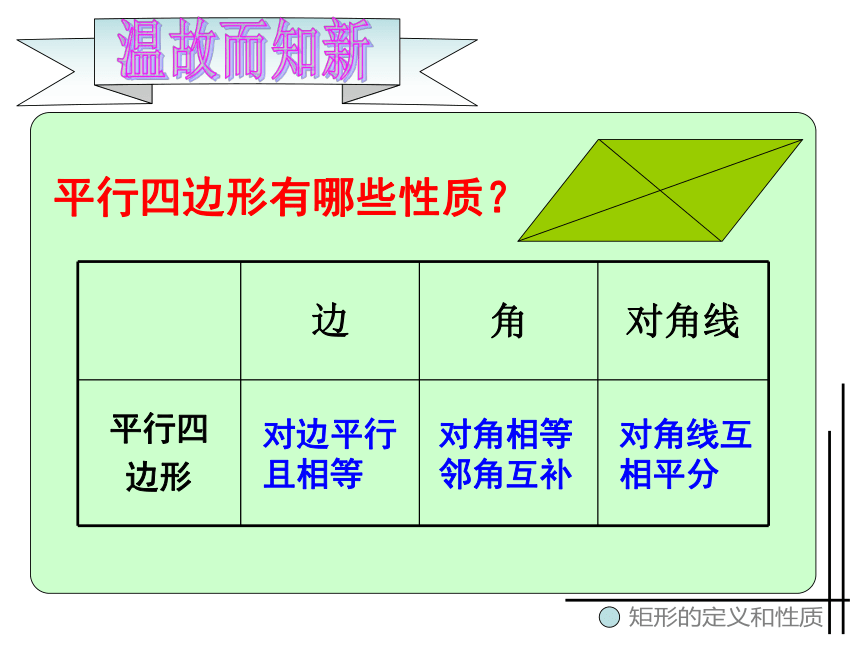
平行四边形有哪些性质?
边 角 对角线
平行四
边形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
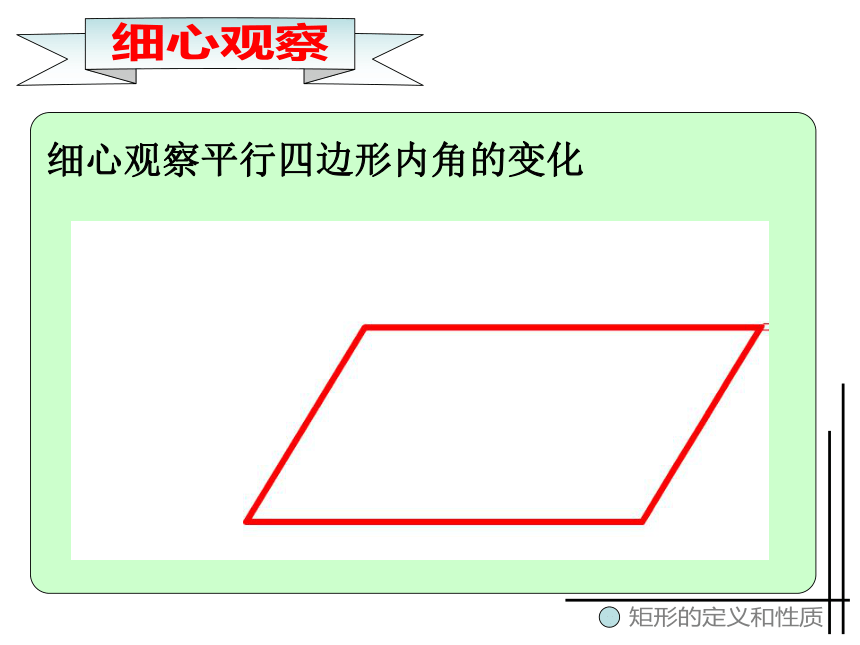
细心观察平行四边形内角的变化
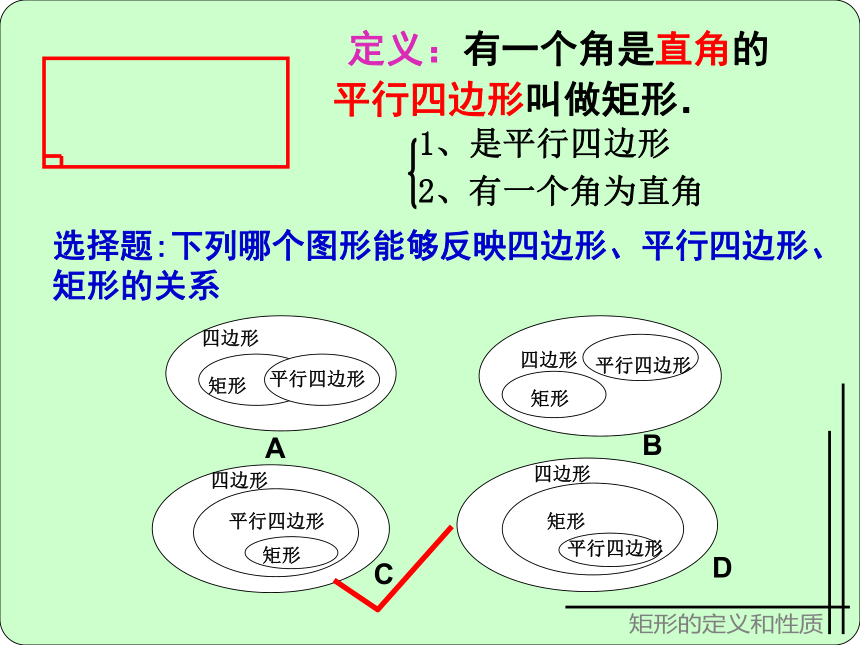
定义:有一个角是直角的平行四边形叫做矩形.
1、是平行四边形
2、有一个角为直角
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
1、平行四边形变成矩形时,图形的内角
有何特征?
2、平行四边形变成矩形时,两条对角线
的长度有什么关系?
在操作过程中,请你思考下列问题:
A
O
D
C
B
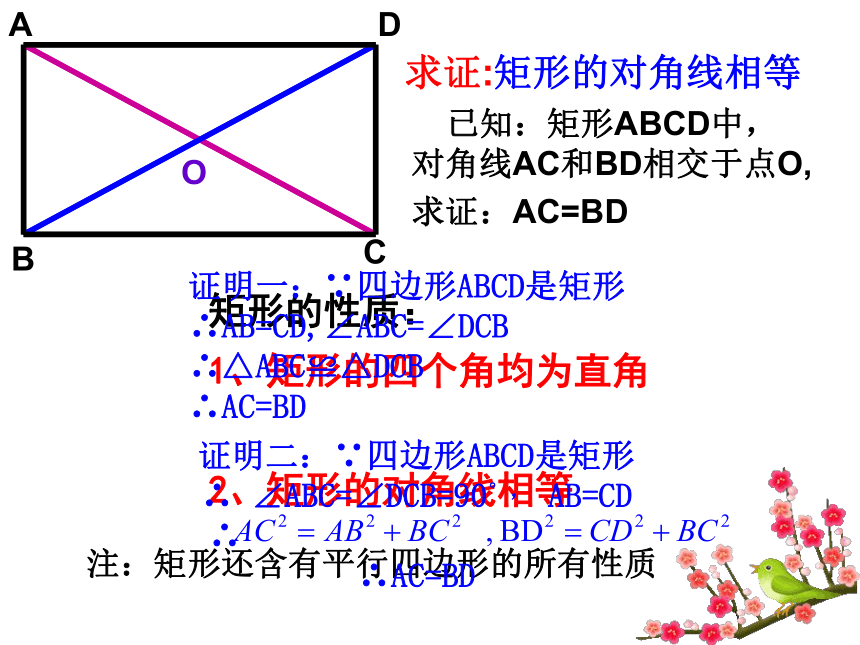
求证:矩形的对角线相等
已知:矩形ABCD中,
对角线AC和BD相交于点O,
求证:AC=BD
矩形的性质:
1、矩形的四个角均为直角
2、矩形的对角线相等
注:矩形还含有平行四边形的所有性质
证明二:∵四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°, AB=CD
∴
∴AC=BD
证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
∴△ABC≌△DCB
∴AC=BD
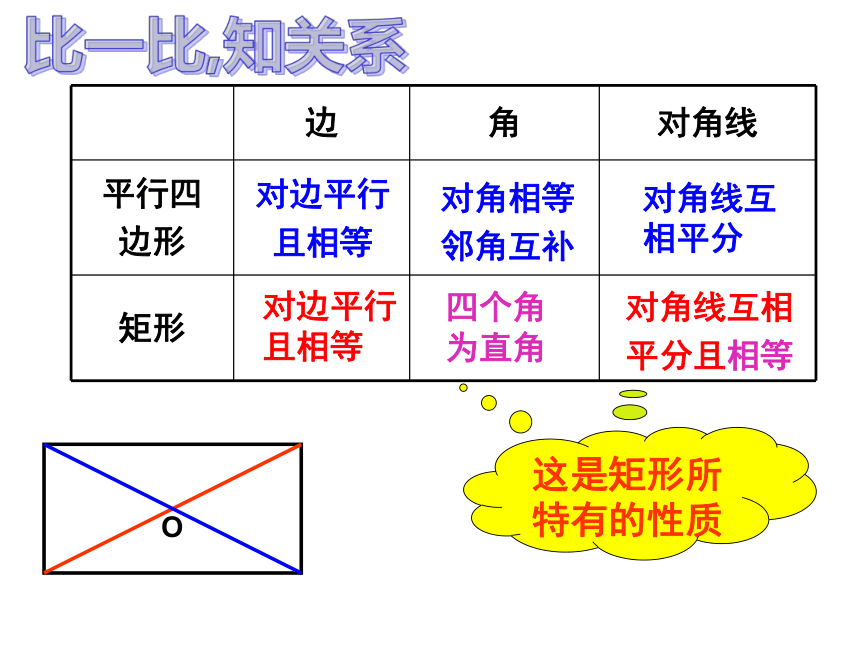
边 角 对角线
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
这是矩形所特有的性质
O
1. 矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分
2、 矩形的一组邻边长分别是3cm和4cm,
则它的对角线长是 cm.
A
5
A
O
D
C
B
直角三角形的性质:
直角三角形斜边上的中线
等于斜边的一半.
即兴练一练:
已知一直角三角形两直角边分别为6和8,则其
斜边上的中线长为________.
5
学有所得
图中我们常见的特殊
三角形有哪些?
B
O
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OD,
又∵∠AOB=60°,
∴OA=AB=4(cm)
∴矩形的对角线AC=BD=2OA=8 ( cm ) .
∴△AOB是等边三角形
已知: 如图,矩形ABCD的
两条对角线交于点O,
AB= 4cm ,∠AOB=60°。
求矩形对角线的长。
D
C
A
1、如图,矩形ABCD的对角线的长为2,∠BDC=300,则矩形ABCD的面积为______.
2、矩形两条对角线所夹的锐角为60°,较短的边长为3.6cm,则对角线的长为_____cm.
7.2
A
D
C
B
A
D
C
B
第1题
第2题
O
3、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____
A
D
C
B
O
16
A
D
C
B
E
1、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。
解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC
注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.
∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4
∵AE平分∠BAD
∴∠BAE=45°
∴AB=BE=4
∴BC=7
∴矩形ABCD的周长为22cm
问题: 体育节中有一投圈游戏,四个同学分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OB=OD = OA=OC
说说:
今天的收获……
你还有什么不明白的地方……
4、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。
3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;
1、矩形定义:
有一个角是直角的平行四边形叫矩形
矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等
2、如图,矩形AEFG和矩形ADCB的大小、形状完全相同,把它们拼成如图所示的L型图案,已知∠FAE=30°,分别求∠1、∠2的度数。
解:依题意可知:
∠FAE=∠DCA=30 °,AF=AC
∴∠1=45 °,
∴∠2=∠ACF-∠ACD=15 °
∴∠DAC=60 °,
∴∠FAC=90 °,
A
B
G
F
E
D
C
H
1
2
如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢
A
C
B
F
E
D
19.2.1 特殊的平行四边形
----矩形的定义和性质
平行四边形有哪些性质?
边 角 对角线
平行四
边形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
细心观察平行四边形内角的变化
定义:有一个角是直角的平行四边形叫做矩形.
1、是平行四边形
2、有一个角为直角
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
1、平行四边形变成矩形时,图形的内角
有何特征?
2、平行四边形变成矩形时,两条对角线
的长度有什么关系?
在操作过程中,请你思考下列问题:
A
O
D
C
B
求证:矩形的对角线相等
已知:矩形ABCD中,
对角线AC和BD相交于点O,
求证:AC=BD
矩形的性质:
1、矩形的四个角均为直角
2、矩形的对角线相等
注:矩形还含有平行四边形的所有性质
证明二:∵四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°, AB=CD
∴
∴AC=BD
证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
∴△ABC≌△DCB
∴AC=BD
边 角 对角线
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
这是矩形所特有的性质
O
1. 矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分
2、 矩形的一组邻边长分别是3cm和4cm,
则它的对角线长是 cm.
A
5
A
O
D
C
B
直角三角形的性质:
直角三角形斜边上的中线
等于斜边的一半.
即兴练一练:
已知一直角三角形两直角边分别为6和8,则其
斜边上的中线长为________.
5
学有所得
图中我们常见的特殊
三角形有哪些?
B
O
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OD,
又∵∠AOB=60°,
∴OA=AB=4(cm)
∴矩形的对角线AC=BD=2OA=8 ( cm ) .
∴△AOB是等边三角形
已知: 如图,矩形ABCD的
两条对角线交于点O,
AB= 4cm ,∠AOB=60°。
求矩形对角线的长。
D
C
A
1、如图,矩形ABCD的对角线的长为2,∠BDC=300,则矩形ABCD的面积为______.
2、矩形两条对角线所夹的锐角为60°,较短的边长为3.6cm,则对角线的长为_____cm.
7.2
A
D
C
B
A
D
C
B
第1题
第2题
O
3、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____
A
D
C
B
O
16
A
D
C
B
E
1、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。
解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC
注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.
∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4
∵AE平分∠BAD
∴∠BAE=45°
∴AB=BE=4
∴BC=7
∴矩形ABCD的周长为22cm
问题: 体育节中有一投圈游戏,四个同学分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OB=OD = OA=OC
说说:
今天的收获……
你还有什么不明白的地方……
4、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。
3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;
1、矩形定义:
有一个角是直角的平行四边形叫矩形
矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等
2、如图,矩形AEFG和矩形ADCB的大小、形状完全相同,把它们拼成如图所示的L型图案,已知∠FAE=30°,分别求∠1、∠2的度数。
解:依题意可知:
∠FAE=∠DCA=30 °,AF=AC
∴∠1=45 °,
∴∠2=∠ACF-∠ACD=15 °
∴∠DAC=60 °,
∴∠FAC=90 °,
A
B
G
F
E
D
C
H
1
2
如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢
A
C
B
F
E
D
