北师大版八年级下册 6.1《平行四边形的性质》教案
文档属性
| 名称 | 北师大版八年级下册 6.1《平行四边形的性质》教案 | 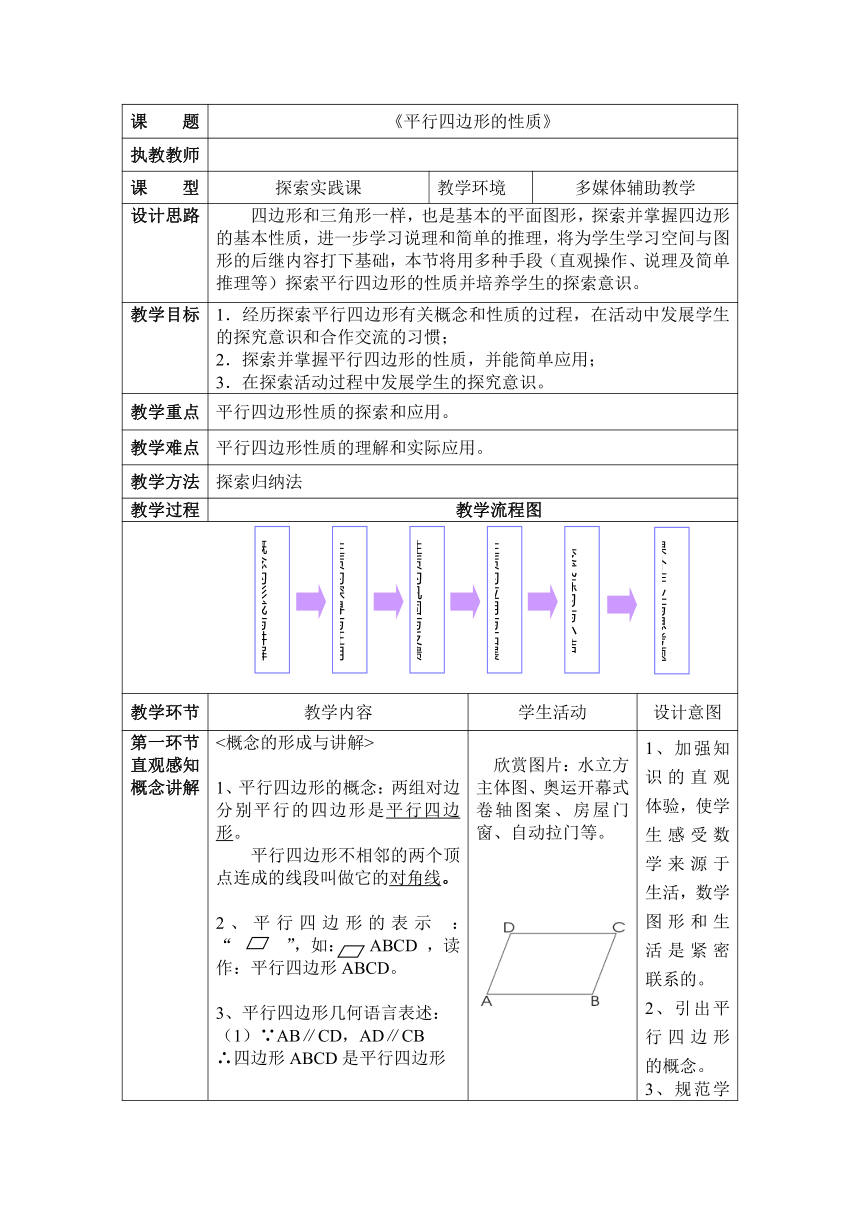 | |
| 格式 | doc | ||
| 文件大小 | 568.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 16:35:27 | ||
图片预览


文档简介
课 题 《平行四边形的性质》
执教教师
课 型 探索实践课 教学环境 多媒体辅助教学
设计思路 四边形和三角形一样,也是基本的平面图形,探索并掌握四边形的基本性质,进一步学习说理和简单的推理,将为学生学习空间与图形的后继内容打下基础,本节将用多种手段(直观操作、说理及简单推理等)探索平行四边形的性质并培养学生的探索意识。
教学目标 1.经历探索平行四边形有关概念和性质的过程,在活动中发展学生的探究意识和合作交流的习惯;
2.探索并掌握平行四边形的性质,并能简单应用;
3.在探索活动过程中发展学生的探究意识。
教学重点 平行四边形性质的探索和应用。
教学难点 平行四边形性质的理解和实际应用。
教学方法 探索归纳法
教学过程 教学流程图
教学环节 教学内容 学生活动 设计意图
第一环节 直观感知概念讲解 <概念的形成与讲解>
1、平行四边形的概念:两组对边分别平行的四边形是平行四边形。
平行四边形不相邻的两个顶点连成的线段叫做它的对角线。
2、平行四边形的表示 :“ ”,如: ABCD ,读作:平行四边形ABCD。
3、平行四边形几何语言表述:
(1)∵AB∥CD,AD∥CB
∴四边形ABCD是平行四边形
(2)∵四边形ABCD是平行四边形
∴AB∥CD,AD∥CB
欣赏图片:水立方主体图、奥运开幕式卷轴图案、房屋门窗、自动拉门等。 1、加强知识的直观体验,使学生感受数学来源于生活,数学图形和生活是紧密联系的。
2、引出平行四边形的概念。
3、规范学生几何语言。
4、讨论:如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有 个,它们是 。
学生分组讨论。
4、强化学生的合作意识,使学生认识到集体力量和团结协作的重要性。
第二环节 探索归纳推理论证 <性质的探寻与证明>
平行四边形的性质:
平行四边形的对边相等,
平行四边形的对角相等。
小组活动:“拼一拼”
准备两个全等的三角形纸片,将相等的一组边重合。
你能拼出平行四边形吗?试一试。
组织数学实践,自主探索,从整体的角度感受平行四边形的性质。
让学生亲自动手操作,用自己制作的两个全等的三角形纸片摆一摆、拼一拼,并注意用眼观察,动脑思考,顺乎自然地得出“两个全等的三角形纸片,将相等的一组边重合,能拼出平行四边形。”的结论,从中领悟出“实践出真知”、“实践第一”的观点。把数学中的原理和方法,转化成学生的一般的世界观和思想方法,对学生进行兴趣、情感、品格教育。
2、性质的证明:
如图连结AC
∵ 四边形ABCD是平行四边形
∴AD // BC, AB // CD
∴ ∠1=∠2,∠3=∠4
∴ 在△ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=CD, AD=CB,∠B =∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠3=∠2+∠4
即∠BAD=∠DCB
方法小结:有关四边形的问题常常可转化为三角形问题来处理。
学生说理
“实践→认识→再实践→再认识”是数学学习的重要方法,通过说理,由直观感受上升到理性分析,在操作层面感知的基础上提升,并了解图形具有的数学本质。
解题方法的小结归纳,旨在渗透“转化”的数学思想,培养学生的发展观念,让学生知道数学内容中存在着的相互联系和相互转化的规律,体会辩证唯物主义的观点。
第三环节 应用巩固 感悟升华 <性质的巩固与反馈>
1、如图:在 ABCD中,根据已知你能得到哪些结论?为什么?
小结:平行四边形中知道其中一个角可求出另外三个角的度数。
2、四边形ABCD是平行四边形,则∠ADC= , ∠BCD= 。AB= ,BC= 。
3、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
进一步理解平行四边形的性质,并进行简单的合情推理,体现性质的应用。
第四环节应用拓展深化提高 <性质的应用与拓展>
例题:已知: AB // EF,BC // DF ;
求证:∠1= ∠F。
变式一:已知:AB//EF,BC//DF,AC//DE ;你还能找到哪些相等的角呢?能说明理由吗?
变式二:如图, AB//EF,BC//DF,AC//DE ;
求证:(1) 点A是DF的中点; (2)A、B、C分别是△DEF各边的中点 。
针对教学和学生实际,改变和开发新的习题,巩固对性质的理解及应用。
变式三:
(实际应用题)
请你来帮忙!
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
学生思考、小组讨论,设计出方案。
引导学生把学到的数学知识用于解决实际问题。
第五环节 评价反思 概括总结 通过本节课的学习,你有什么收获?
2、平行四边形的概念、性质。
学生踊跃谈感受和收获。
鼓励学生交流课堂实践、观察探索的经历、感受和收获;鼓励学生勇于进行自我评价,进一步培养学生反思意识及总结能力。
第六环节布置作业
1.课本习题4.1 1,2,3.
2.思考题
如图 ABCD中,平行于对角线BD的直线MN分别交CD,CB的延长线于M,N,交AD于点P,交AB于点Q,你能说明MQ=NP吗?说说你的理由。
1.通过作业巩固对平行四边形性质理解并学会应用。
2.思考题,旨在继续延伸学生的探究意识。
板书设计 平行四边形的性质
一、平行四边形的概念: 二、平行四边形的性质: 三、例题
教学反思 本节教材直观感知活动较多,由学生的心理及年龄特点决定,学生有一定的逻辑思考能力及说理能力,因此从理性角度分析平行四边形的性质特点是非常需要的。还要引导有条理的叙述及数学语言的表达。
执教教师
课 型 探索实践课 教学环境 多媒体辅助教学
设计思路 四边形和三角形一样,也是基本的平面图形,探索并掌握四边形的基本性质,进一步学习说理和简单的推理,将为学生学习空间与图形的后继内容打下基础,本节将用多种手段(直观操作、说理及简单推理等)探索平行四边形的性质并培养学生的探索意识。
教学目标 1.经历探索平行四边形有关概念和性质的过程,在活动中发展学生的探究意识和合作交流的习惯;
2.探索并掌握平行四边形的性质,并能简单应用;
3.在探索活动过程中发展学生的探究意识。
教学重点 平行四边形性质的探索和应用。
教学难点 平行四边形性质的理解和实际应用。
教学方法 探索归纳法
教学过程 教学流程图
教学环节 教学内容 学生活动 设计意图
第一环节 直观感知概念讲解 <概念的形成与讲解>
1、平行四边形的概念:两组对边分别平行的四边形是平行四边形。
平行四边形不相邻的两个顶点连成的线段叫做它的对角线。
2、平行四边形的表示 :“ ”,如: ABCD ,读作:平行四边形ABCD。
3、平行四边形几何语言表述:
(1)∵AB∥CD,AD∥CB
∴四边形ABCD是平行四边形
(2)∵四边形ABCD是平行四边形
∴AB∥CD,AD∥CB
欣赏图片:水立方主体图、奥运开幕式卷轴图案、房屋门窗、自动拉门等。 1、加强知识的直观体验,使学生感受数学来源于生活,数学图形和生活是紧密联系的。
2、引出平行四边形的概念。
3、规范学生几何语言。
4、讨论:如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有 个,它们是 。
学生分组讨论。
4、强化学生的合作意识,使学生认识到集体力量和团结协作的重要性。
第二环节 探索归纳推理论证 <性质的探寻与证明>
平行四边形的性质:
平行四边形的对边相等,
平行四边形的对角相等。
小组活动:“拼一拼”
准备两个全等的三角形纸片,将相等的一组边重合。
你能拼出平行四边形吗?试一试。
组织数学实践,自主探索,从整体的角度感受平行四边形的性质。
让学生亲自动手操作,用自己制作的两个全等的三角形纸片摆一摆、拼一拼,并注意用眼观察,动脑思考,顺乎自然地得出“两个全等的三角形纸片,将相等的一组边重合,能拼出平行四边形。”的结论,从中领悟出“实践出真知”、“实践第一”的观点。把数学中的原理和方法,转化成学生的一般的世界观和思想方法,对学生进行兴趣、情感、品格教育。
2、性质的证明:
如图连结AC
∵ 四边形ABCD是平行四边形
∴AD // BC, AB // CD
∴ ∠1=∠2,∠3=∠4
∴ 在△ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=CD, AD=CB,∠B =∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠3=∠2+∠4
即∠BAD=∠DCB
方法小结:有关四边形的问题常常可转化为三角形问题来处理。
学生说理
“实践→认识→再实践→再认识”是数学学习的重要方法,通过说理,由直观感受上升到理性分析,在操作层面感知的基础上提升,并了解图形具有的数学本质。
解题方法的小结归纳,旨在渗透“转化”的数学思想,培养学生的发展观念,让学生知道数学内容中存在着的相互联系和相互转化的规律,体会辩证唯物主义的观点。
第三环节 应用巩固 感悟升华 <性质的巩固与反馈>
1、如图:在 ABCD中,根据已知你能得到哪些结论?为什么?
小结:平行四边形中知道其中一个角可求出另外三个角的度数。
2、四边形ABCD是平行四边形,则∠ADC= , ∠BCD= 。AB= ,BC= 。
3、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
进一步理解平行四边形的性质,并进行简单的合情推理,体现性质的应用。
第四环节应用拓展深化提高 <性质的应用与拓展>
例题:已知: AB // EF,BC // DF ;
求证:∠1= ∠F。
变式一:已知:AB//EF,BC//DF,AC//DE ;你还能找到哪些相等的角呢?能说明理由吗?
变式二:如图, AB//EF,BC//DF,AC//DE ;
求证:(1) 点A是DF的中点; (2)A、B、C分别是△DEF各边的中点 。
针对教学和学生实际,改变和开发新的习题,巩固对性质的理解及应用。
变式三:
(实际应用题)
请你来帮忙!
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
学生思考、小组讨论,设计出方案。
引导学生把学到的数学知识用于解决实际问题。
第五环节 评价反思 概括总结 通过本节课的学习,你有什么收获?
2、平行四边形的概念、性质。
学生踊跃谈感受和收获。
鼓励学生交流课堂实践、观察探索的经历、感受和收获;鼓励学生勇于进行自我评价,进一步培养学生反思意识及总结能力。
第六环节布置作业
1.课本习题4.1 1,2,3.
2.思考题
如图 ABCD中,平行于对角线BD的直线MN分别交CD,CB的延长线于M,N,交AD于点P,交AB于点Q,你能说明MQ=NP吗?说说你的理由。
1.通过作业巩固对平行四边形性质理解并学会应用。
2.思考题,旨在继续延伸学生的探究意识。
板书设计 平行四边形的性质
一、平行四边形的概念: 二、平行四边形的性质: 三、例题
教学反思 本节教材直观感知活动较多,由学生的心理及年龄特点决定,学生有一定的逻辑思考能力及说理能力,因此从理性角度分析平行四边形的性质特点是非常需要的。还要引导有条理的叙述及数学语言的表达。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
