北师大版八年级下册 6.3《三角形的中位线》教案(表格式)
文档属性
| 名称 | 北师大版八年级下册 6.3《三角形的中位线》教案(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 16:35:27 | ||
图片预览

文档简介
授课题目 §6.3三角形的中位线 授课时间
类 别 教读课( ) 自读课( )新授课(√ ) 实验实践课( ) 复习课( )
任课教师 教学方法 归纳、引导、观察、探索、猜想、验证、兵教兵、合作交流
授课班级 八、一 课时安排
知识与 能 力 1.知道三角形中位线的概念。
2.理解三角形中位线定理,并能运用它进行有关的论证和计算。
3.通过对问题的探索及进一步变式,培养学生逆向思维及分解构造基本图形解决较复杂问题的能力.
过程与 方 法 1.经历探索、猜想、验证、发现概念和定理形成过程,渗透化归思想。
2.引导学生积极经历实验与观察、分析与比较、讨论与释疑、概括与归纳、巩固与提高等科学有效的学习方法。
情感态度 与价值观 1、培养学生科学分析的态度和积极的探索精神,激发学生学习的积极性,进一步提高学生学习数学的兴趣和信心。
2、经历观察、探索、交流、合作、归纳、应用等环节,形成良好的学习态度和学习方法。
教学准备: 教师准备:几何画板课件、导学案、高效课堂教案
学生准备:导学案、教材、辅导材料、彩纸、直尺、铅笔、黑色签字笔、剪刀等
教学重点及难点预测: 重点:应用三角形中位线定理解决有关问题。
难点:三角形中位线定理的验证与应用。
教学步骤及设计
教师活动 学生活动 教学手段
一、创设情境
几何画板课件呈现以下三张图片:
学生认真观察与思考,学生带着疑问走进§26.3三角形的中位线的学习
几何画板
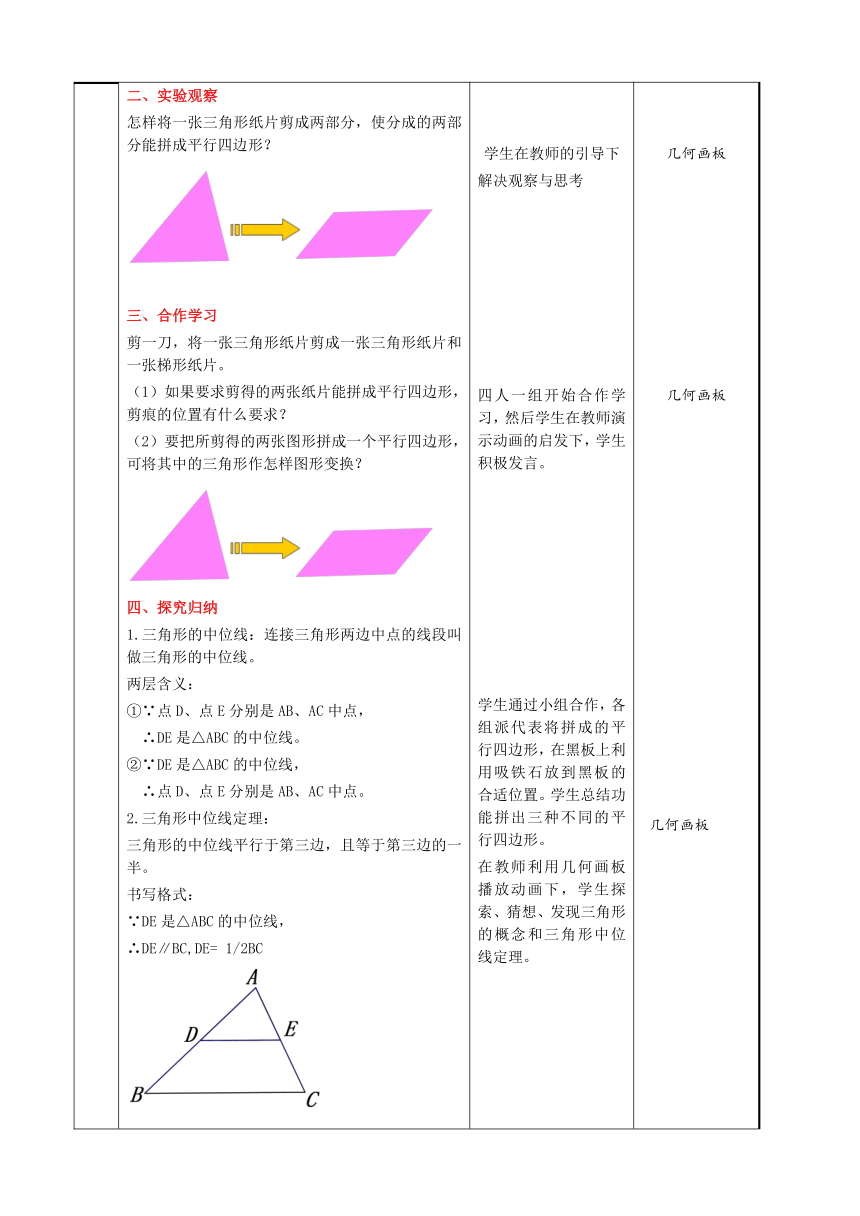
二、实验观察
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成平行四边形?
三、合作学习
剪一刀,将一张三角形纸片剪成一张三角形纸片和一张梯形纸片。
(1)如果要求剪得的两张纸片能拼成平行四边形,剪痕的位置有什么要求?
(2)要把所剪得的两张图形拼成一个平行四边形,可将其中的三角形作怎样图形变换?
四、探究归纳
1.三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线。
两层含义:
①∵点D、点E分别是AB、AC中点,
∴DE是△ABC的中位线。
②∵DE是△ABC的中位线,
∴点D、点E分别是AB、AC中点。
2.三角形中位线定理:
三角形的中位线平行于第三边,且等于第三边的一半。
书写格式:
∵DE是△ABC的中位线,
∴DE∥BC,DE= 1/2BC
学生在教师的引导下
解决观察与思考
四人一组开始合作学习,然后学生在教师演示动画的启发下,学生积极发言。
学生通过小组合作,各组派代表将拼成的平行四边形,在黑板上利用吸铁石放到黑板的合适位置。学生总结功能拼出三种不同的平行四边形。
在教师利用几何画板播放动画下,学生探索、猜想、发现三角形的概念和三角形中位线定理。
几何画板
几何画板
几何画板
教学步骤及设计
五、理论证明
延长DE至F使DE=FE,连接AF、FC、CD,
∵AE=CE
∴四边形ADCF是平行四边形。
∴AD∥CF,AD=CF
∵AD=BD,
∴BD∥CF,BD=CF
∴四边形BDFC是平行四边形。
∴DF∥BC,DF=BC.
∴DE∥BC,DE=BC。
六、解决问题
如图,A,B两地被池塘隔开,在A,B外选一点C,连接AC,BC的中点M,N,如果测得MN=20cm,那么A,B间距离为_________
七、智海扬帆
如图,任意四边形,以四边的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流。
学生小组合作或独立完成证明过程,然后各组派代表上台,利用录播教室是投影仪展示与讲解。
学生根据定理快速口答
学生小组合作,然后组长派代表到台上,在投影仪上展示讲解。
几何画板
几何画板
几何画板
八、链接中考
如图,四边形ABCD中,若AB=CD,E、F、H分别是BC、AD、BD的中点,BA,EF的延长线交于点M,EF,CD的延长线交于点N,则FH______EH
(“=”或“<”或“>” )
九、总结提升
本节课你收获了吗?有疑惑吗?和大家分享一下好吗?
学生在教师的引导下启发下,会很容易说出答案,然后教师提出∠AME和∠DNE呢?
学生畅所欲言,互相补充,教师做最后的升华总结,同时学生认真聆听。
几何画板
几何画板
八、布置作业 必做:习题6.6第1,2,3题;
选做:习题6.6第4题。
板书设计 §6.3三角形的中位线
1.三角形的中位线概念 2.三角形中位线定理
两层含义: 书写格式:
类 别 教读课( ) 自读课( )新授课(√ ) 实验实践课( ) 复习课( )
任课教师 教学方法 归纳、引导、观察、探索、猜想、验证、兵教兵、合作交流
授课班级 八、一 课时安排
知识与 能 力 1.知道三角形中位线的概念。
2.理解三角形中位线定理,并能运用它进行有关的论证和计算。
3.通过对问题的探索及进一步变式,培养学生逆向思维及分解构造基本图形解决较复杂问题的能力.
过程与 方 法 1.经历探索、猜想、验证、发现概念和定理形成过程,渗透化归思想。
2.引导学生积极经历实验与观察、分析与比较、讨论与释疑、概括与归纳、巩固与提高等科学有效的学习方法。
情感态度 与价值观 1、培养学生科学分析的态度和积极的探索精神,激发学生学习的积极性,进一步提高学生学习数学的兴趣和信心。
2、经历观察、探索、交流、合作、归纳、应用等环节,形成良好的学习态度和学习方法。
教学准备: 教师准备:几何画板课件、导学案、高效课堂教案
学生准备:导学案、教材、辅导材料、彩纸、直尺、铅笔、黑色签字笔、剪刀等
教学重点及难点预测: 重点:应用三角形中位线定理解决有关问题。
难点:三角形中位线定理的验证与应用。
教学步骤及设计
教师活动 学生活动 教学手段
一、创设情境
几何画板课件呈现以下三张图片:
学生认真观察与思考,学生带着疑问走进§26.3三角形的中位线的学习
几何画板
二、实验观察
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成平行四边形?
三、合作学习
剪一刀,将一张三角形纸片剪成一张三角形纸片和一张梯形纸片。
(1)如果要求剪得的两张纸片能拼成平行四边形,剪痕的位置有什么要求?
(2)要把所剪得的两张图形拼成一个平行四边形,可将其中的三角形作怎样图形变换?
四、探究归纳
1.三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线。
两层含义:
①∵点D、点E分别是AB、AC中点,
∴DE是△ABC的中位线。
②∵DE是△ABC的中位线,
∴点D、点E分别是AB、AC中点。
2.三角形中位线定理:
三角形的中位线平行于第三边,且等于第三边的一半。
书写格式:
∵DE是△ABC的中位线,
∴DE∥BC,DE= 1/2BC
学生在教师的引导下
解决观察与思考
四人一组开始合作学习,然后学生在教师演示动画的启发下,学生积极发言。
学生通过小组合作,各组派代表将拼成的平行四边形,在黑板上利用吸铁石放到黑板的合适位置。学生总结功能拼出三种不同的平行四边形。
在教师利用几何画板播放动画下,学生探索、猜想、发现三角形的概念和三角形中位线定理。
几何画板
几何画板
几何画板
教学步骤及设计
五、理论证明
延长DE至F使DE=FE,连接AF、FC、CD,
∵AE=CE
∴四边形ADCF是平行四边形。
∴AD∥CF,AD=CF
∵AD=BD,
∴BD∥CF,BD=CF
∴四边形BDFC是平行四边形。
∴DF∥BC,DF=BC.
∴DE∥BC,DE=BC。
六、解决问题
如图,A,B两地被池塘隔开,在A,B外选一点C,连接AC,BC的中点M,N,如果测得MN=20cm,那么A,B间距离为_________
七、智海扬帆
如图,任意四边形,以四边的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流。
学生小组合作或独立完成证明过程,然后各组派代表上台,利用录播教室是投影仪展示与讲解。
学生根据定理快速口答
学生小组合作,然后组长派代表到台上,在投影仪上展示讲解。
几何画板
几何画板
几何画板
八、链接中考
如图,四边形ABCD中,若AB=CD,E、F、H分别是BC、AD、BD的中点,BA,EF的延长线交于点M,EF,CD的延长线交于点N,则FH______EH
(“=”或“<”或“>” )
九、总结提升
本节课你收获了吗?有疑惑吗?和大家分享一下好吗?
学生在教师的引导下启发下,会很容易说出答案,然后教师提出∠AME和∠DNE呢?
学生畅所欲言,互相补充,教师做最后的升华总结,同时学生认真聆听。
几何画板
几何画板
八、布置作业 必做:习题6.6第1,2,3题;
选做:习题6.6第4题。
板书设计 §6.3三角形的中位线
1.三角形的中位线概念 2.三角形中位线定理
两层含义: 书写格式:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
