人教版数学四年级下册5.3三角形的内角和课件(33张PPT)
文档属性
| 名称 | 人教版数学四年级下册5.3三角形的内角和课件(33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 06:25:39 | ||
图片预览


文档简介
三角形的内角和
三角形
数学四年级下册(RJ) 教学课件
5
30°
60°
90°
45°
90°
45°
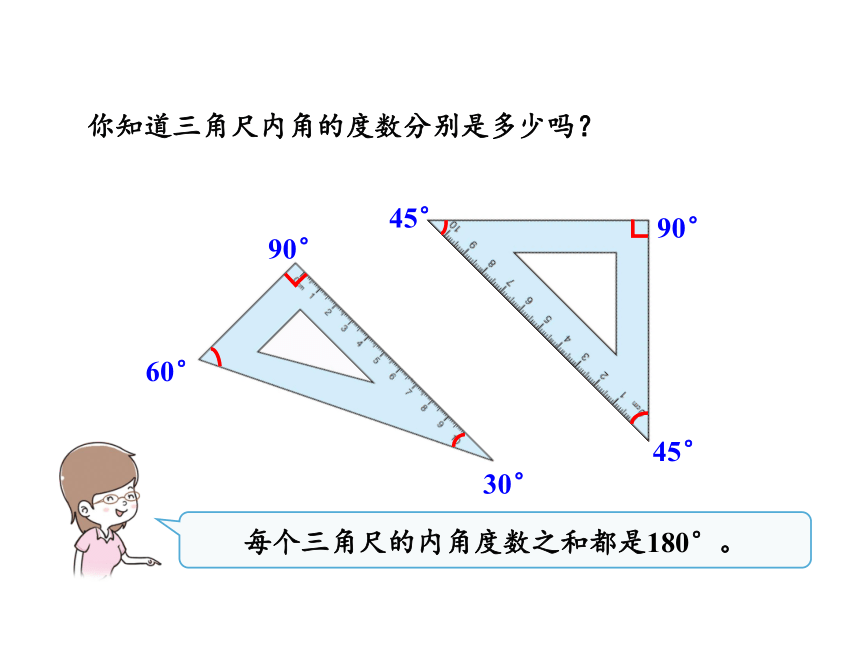
你知道三角尺内角的度数分别是多少吗?
每个三角尺的内角度数之和都是180°。
30°
30°
60°
60°
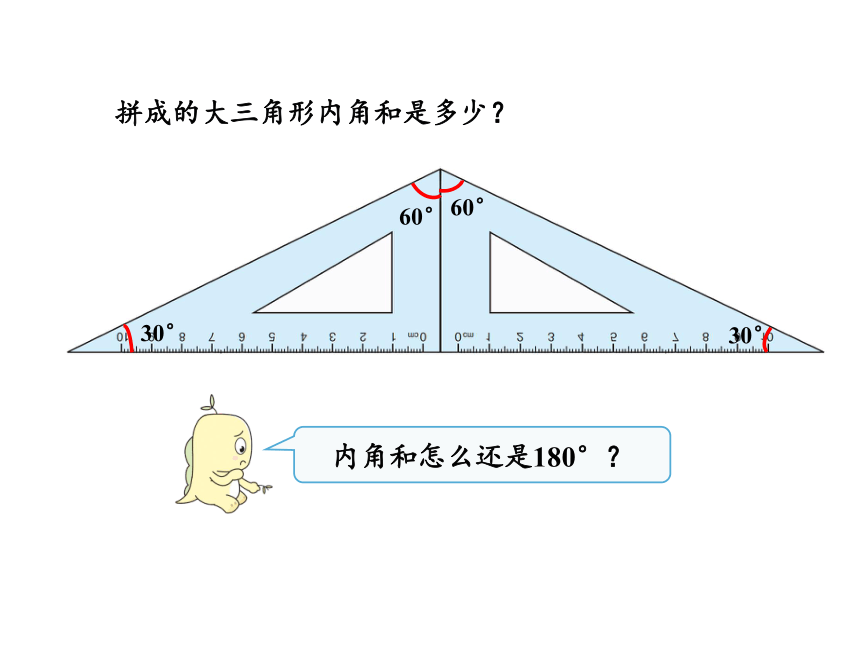
拼成的大三角形内角和是多少?
内角和怎么还是180°?
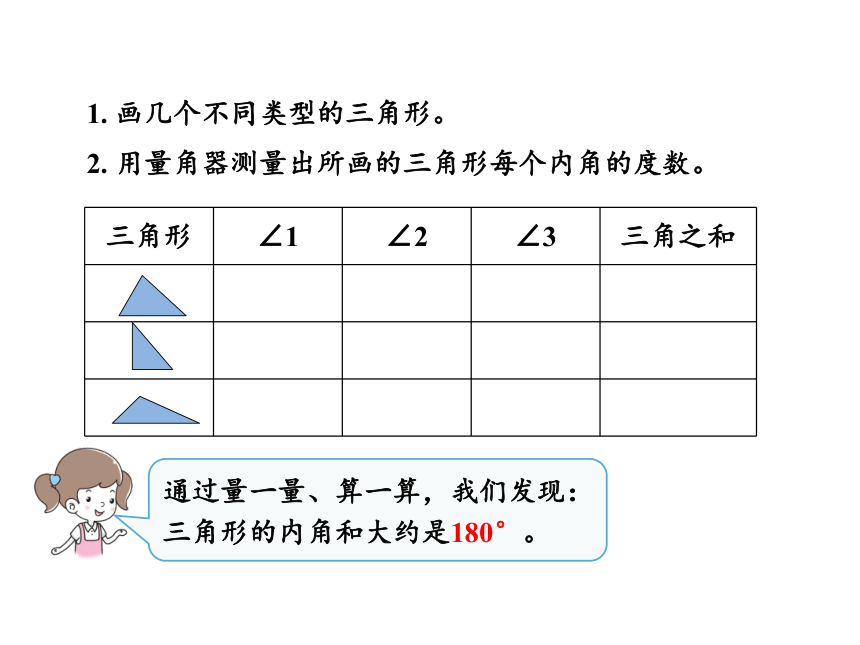
1. 画几个不同类型的三角形。
2. 用量角器测量出所画的三角形每个内角的度数。
三角形
∠1
∠2
∠3
三角之和
通过量一量、算一算,我们发现:三角形的内角和大约是180°。
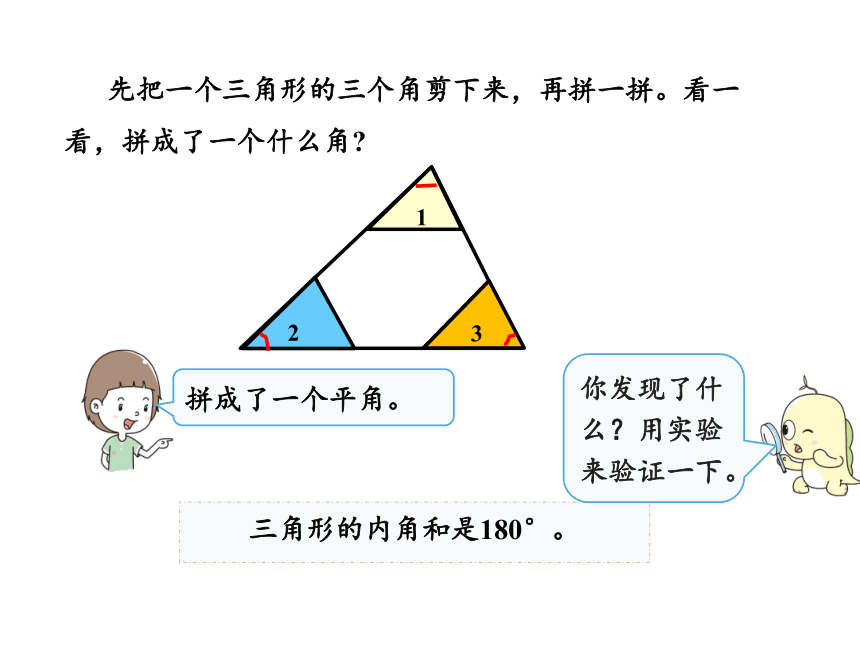
先把一个三角形的三个角剪下来,再拼一拼。看一看,拼成了一个什么角?
1
3
2
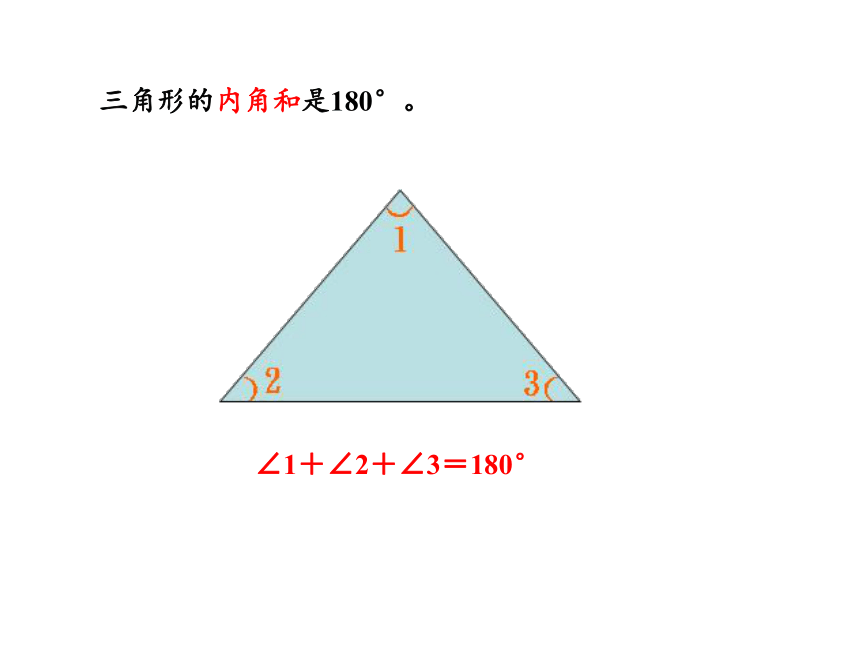
三角形的内角和是180°。
拼成了一个平角。
你发现了什么?用实验来验证一下。
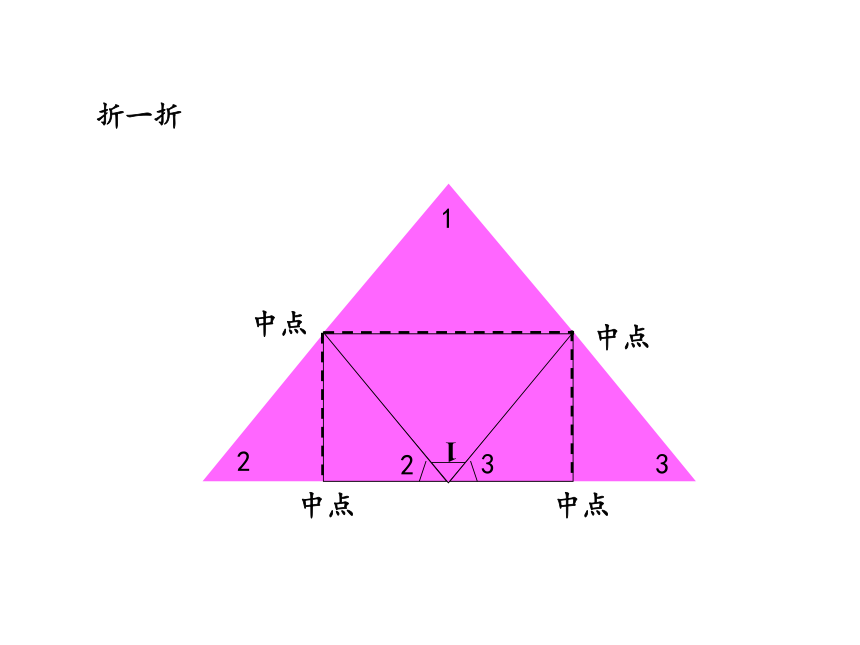
1
中点
中点
中点
中点
折一折
三角形的内角和是180°。
∠1+∠2+∠3=180°
简单练习
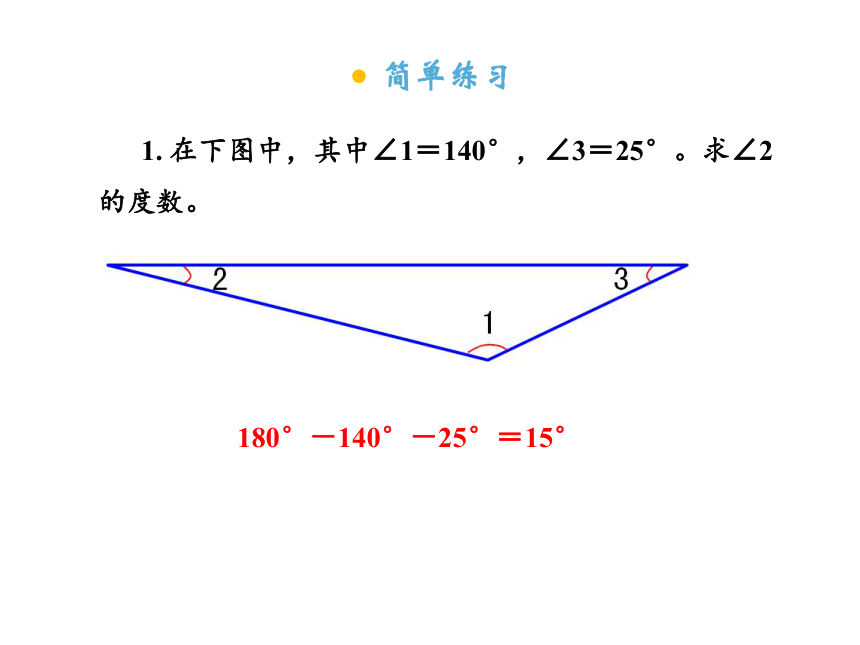
1. 在下图中,其中∠1=140°,∠3=25°。求∠2的度数。
180°-140°-25°=15°
1
4
1
2
3
4
2
3
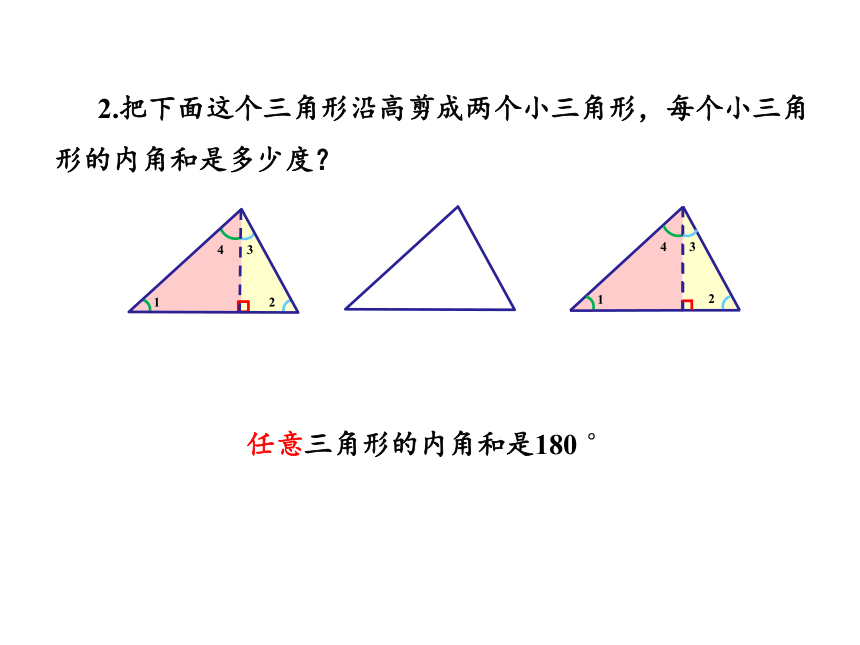
2.把下面这个三角形沿高剪成两个小三角形,每个小三角形的内角和是多少度?
任意三角形的内角和是180 °
(2) 60°,70°,90°
(3) 30°,40°,50°
(4) 50°,50°,80°
(5) 60°,60°,60°
(1) 80°,95°,5°
3.(口答)下列各组角是同一个三角形的内角吗?为什么?
中等练习
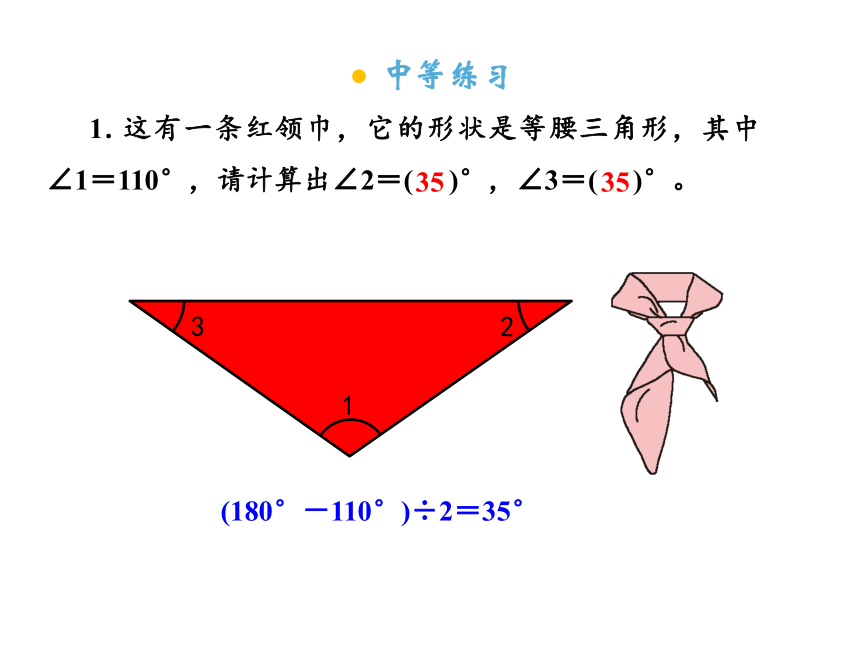
1. 这有一条红领巾,它的形状是等腰三角形,其中∠1=110°,请计算出∠2=( )°,∠3=( )°。
(180°-110°)÷2=35°
35
35
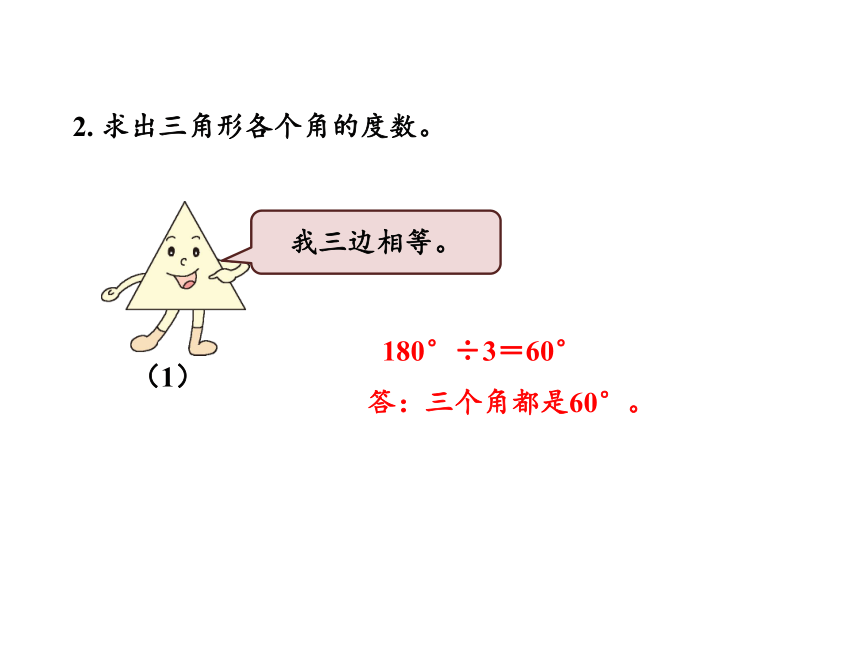
2. 求出三角形各个角的度数。
(1)
我三边相等。
180°÷3=60°
答:三个角都是60°。
(2)
我是等腰三角形,顶角是96°。
180°-96°=84°
84°÷2=42°
答:三个角的度数分别是96°、42°、42°。
(3)
我有一个锐角是40°。
180°-90°-40°
=90°-40°
=50°
答:三个角的度数分别是90°、40°、50°。
拓展练习
某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去。为什么?
③
第一块和第二块只保留了原三角形的一个角和部分边……
第三块不仅保留了原来三角形的两个角还保留了一边。
本节课你都有哪些收获?
(1)我们分别用度量、剪拼、折一折的方法对三角形的内角和进行验证,三角形内角和是180°。
(2)运用三角形内角和是180°的知识来解决生活中的问题。
1. 练习十六,第1题。
2. 练习十六,第3题。
数学四年级下册(RJ) 教学课件
谢谢!
多边形的内角和
三角形
数学四年级下册(RJ) 教学课件
5
三角形内角和等于 。
三角形:
三角形有 条边, 个顶点, 个角。
180°
3
3
四边形:
四边形有 条边, 个顶点, 个角。
4
4
3
4
四边形都包括哪些?
所有的四边形的内角和是一样的吗?
360°
特殊的四边形
一般的四边形
所有的三角形内角和都是180 °
如果一样,猜一猜是多少度。
长方形、正方形的四个角都是直角,所以长方形、正方形的内角和是360°。
用什么办法求出其他四边形的内角和呢?
四边形的内角和是360°。
量一量 算一算。
1
2
3
4
1
2
3
4
拼成了一个周角。
四边形的内角和是360°。
剪一剪 拼一拼。
运用三角形的内角和知识。
180°+180°=360°
四边形的内角和是360°
或180°×2 =360°
分成了2个三角形。
简单练习
你能想办法求出这个多边形的内角和吗?
把这个六边形分成了4个三角形,180°×4=720°。
中等练习
1. 画一画,算一算,你发现了什么?
6
7
2
3
180?×5
180?×4
发现:多边形的内角和=180°×(边数-2)
2. 下面图形中各有多少个三角形?有什么规律?
1个
3个
6个
10个
拓展练习
一个三角形中,最大角是最小角的3倍,另一个角是最小角的2倍,按角分,这个三角形是什么三角形?
180? ÷(3+2+1)
= 180? ÷6
= 30?
30? ×3=90?
答:这个三角形是直角三角形。
四边形的
内角和的
推导
剪拼:把四个角剪下来,拼在一起拼成了一
个周角。
分割:把四边形分成了两个三角形,所以四
边形的内角和是180°乘2得360°。
量算:用量角器量出四个角的度数,加起来
大约是360°。
结论:四边形的内角和都是360°。
多边形的内角和=180°×(边数-2)
练习十六,第6题。
数学四年级下册(RJ) 教学课件
谢谢!
三角形
数学四年级下册(RJ) 教学课件
5
30°
60°
90°
45°
90°
45°
你知道三角尺内角的度数分别是多少吗?
每个三角尺的内角度数之和都是180°。
30°
30°
60°
60°
拼成的大三角形内角和是多少?
内角和怎么还是180°?
1. 画几个不同类型的三角形。
2. 用量角器测量出所画的三角形每个内角的度数。
三角形
∠1
∠2
∠3
三角之和
通过量一量、算一算,我们发现:三角形的内角和大约是180°。
先把一个三角形的三个角剪下来,再拼一拼。看一看,拼成了一个什么角?
1
3
2
三角形的内角和是180°。
拼成了一个平角。
你发现了什么?用实验来验证一下。
1
中点
中点
中点
中点
折一折
三角形的内角和是180°。
∠1+∠2+∠3=180°
简单练习
1. 在下图中,其中∠1=140°,∠3=25°。求∠2的度数。
180°-140°-25°=15°
1
4
1
2
3
4
2
3
2.把下面这个三角形沿高剪成两个小三角形,每个小三角形的内角和是多少度?
任意三角形的内角和是180 °
(2) 60°,70°,90°
(3) 30°,40°,50°
(4) 50°,50°,80°
(5) 60°,60°,60°
(1) 80°,95°,5°
3.(口答)下列各组角是同一个三角形的内角吗?为什么?
中等练习
1. 这有一条红领巾,它的形状是等腰三角形,其中∠1=110°,请计算出∠2=( )°,∠3=( )°。
(180°-110°)÷2=35°
35
35
2. 求出三角形各个角的度数。
(1)
我三边相等。
180°÷3=60°
答:三个角都是60°。
(2)
我是等腰三角形,顶角是96°。
180°-96°=84°
84°÷2=42°
答:三个角的度数分别是96°、42°、42°。
(3)
我有一个锐角是40°。
180°-90°-40°
=90°-40°
=50°
答:三个角的度数分别是90°、40°、50°。
拓展练习
某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去。为什么?
③
第一块和第二块只保留了原三角形的一个角和部分边……
第三块不仅保留了原来三角形的两个角还保留了一边。
本节课你都有哪些收获?
(1)我们分别用度量、剪拼、折一折的方法对三角形的内角和进行验证,三角形内角和是180°。
(2)运用三角形内角和是180°的知识来解决生活中的问题。
1. 练习十六,第1题。
2. 练习十六,第3题。
数学四年级下册(RJ) 教学课件
谢谢!
多边形的内角和
三角形
数学四年级下册(RJ) 教学课件
5
三角形内角和等于 。
三角形:
三角形有 条边, 个顶点, 个角。
180°
3
3
四边形:
四边形有 条边, 个顶点, 个角。
4
4
3
4
四边形都包括哪些?
所有的四边形的内角和是一样的吗?
360°
特殊的四边形
一般的四边形
所有的三角形内角和都是180 °
如果一样,猜一猜是多少度。
长方形、正方形的四个角都是直角,所以长方形、正方形的内角和是360°。
用什么办法求出其他四边形的内角和呢?
四边形的内角和是360°。
量一量 算一算。
1
2
3
4
1
2
3
4
拼成了一个周角。
四边形的内角和是360°。
剪一剪 拼一拼。
运用三角形的内角和知识。
180°+180°=360°
四边形的内角和是360°
或180°×2 =360°
分成了2个三角形。
简单练习
你能想办法求出这个多边形的内角和吗?
把这个六边形分成了4个三角形,180°×4=720°。
中等练习
1. 画一画,算一算,你发现了什么?
6
7
2
3
180?×5
180?×4
发现:多边形的内角和=180°×(边数-2)
2. 下面图形中各有多少个三角形?有什么规律?
1个
3个
6个
10个
拓展练习
一个三角形中,最大角是最小角的3倍,另一个角是最小角的2倍,按角分,这个三角形是什么三角形?
180? ÷(3+2+1)
= 180? ÷6
= 30?
30? ×3=90?
答:这个三角形是直角三角形。
四边形的
内角和的
推导
剪拼:把四个角剪下来,拼在一起拼成了一
个周角。
分割:把四边形分成了两个三角形,所以四
边形的内角和是180°乘2得360°。
量算:用量角器量出四个角的度数,加起来
大约是360°。
结论:四边形的内角和都是360°。
多边形的内角和=180°×(边数-2)
练习十六,第6题。
数学四年级下册(RJ) 教学课件
谢谢!
