人教B版(2019)高中数学必修第四册9.1.1正弦定理第2课时正弦定理的应用课件(共40张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第四册9.1.1正弦定理第2课时正弦定理的应用课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 615.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 00:00:00 | ||
图片预览










文档简介
(共40张PPT)
第2课时 正弦定理的应用
第一篇
教材过关
情景导学
精读教材·必备知识
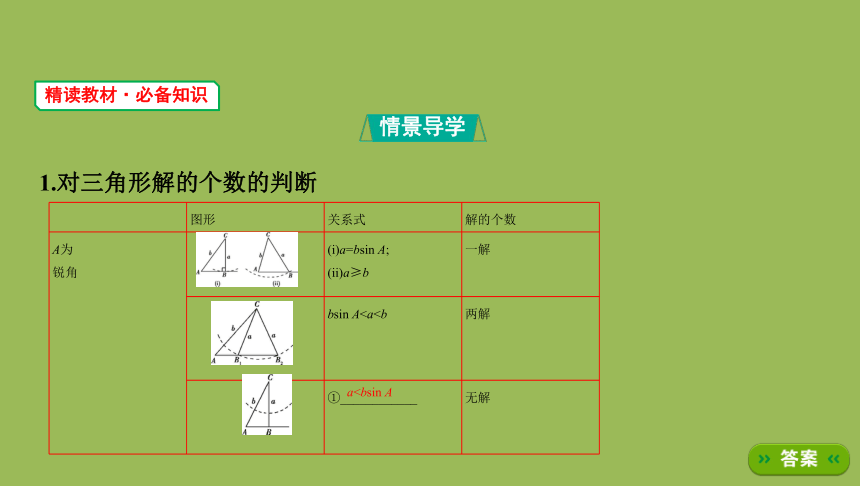
1.对三角形解的个数的判断
图形
关系式
解的个数
A为
锐角
?
(i)a=bsin
A;
(ii)a≥b
一解
?
bsin
A两解
?
①____________
无解
aA
A为钝
角或
直角
?
a>b
一解
?
a≤b
无解
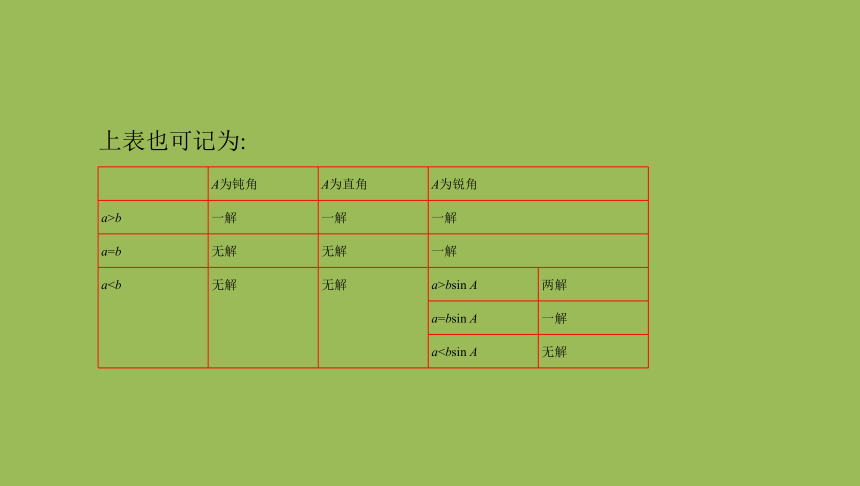
上表也可记为:
A为钝角
A为直角
A为锐角
a>b
一解
一解
一解
a=b
无解
无解
一解
a无解
无解
a>bsin
A
两解
a=bsin
A
一解
aA
无解
特别提醒
已知三角形的两角和任意一边,求另两边和另一角,此时有唯一解,三角形被唯
一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两
解或无解的情况,三角形不能被唯一确定.
2.三角形的面积公式
任意三角形的面积公式为:
S△ABC=?bcsin
A=②_________=③__________.
即任意三角形的面积等于任意两边与它们夹角的正弦值的乘积的一半.
提示 ①S△ABC=?ah,其中a为△ABC的一边长,h为该边上的高.
②S△ABC=?r(a+b+c)=?rl,其中r,l分别为△ABC的内切圆半径及△ABC的周长.
思考:除了上面提到的三角形面积公式,你还能想到其他的三角形面积公式吗?
例1 (1)在△ABC中,角A,B,C的对边分别是a,b,c,已知a=2,B=45°,b=1,则满足条
件的三角形的个数为?( )
A.0 ????B.1
C.2 ????D.无数
(2)(多选)在△ABC中,角A,B,C的对边分别是a,b,c,根据下列条件解三角形,其中
有两解的是?( )
A.b=10,A=45°,C=70°
B.b=45,c=48,B=60°
C.a=14,b=16,A=45°
D.a=7,b=5,A=80°
A
BC
互动探究·关键能力
探究一 三角形解的个数的判断
解析 (1)由?=?,得sin
A=?>1,所以满足条件的三角形的个数是0.
故选A.
(2)选项B满足csin
60°45°对于选项A,可求得B=180°-A-C=65°,三角形有一解,
对于选项D,由sin
B=?,且b故选BC.
思维突破
已知两边和其中一边的对角解三角形时,首先求出另一边的对角的正弦值,再
利用该正弦值求角,此时要根据已知两边的大小情况来确定该角有一个值还
是两个值,或者根据该正弦值(不等于1时)在0°~180°范围内求角,一个锐角,一
个钝角,只要不与三角形内角和定理矛盾,就是所求.
跟踪训练
1-1 已知下列各三角形中的两边及其一边的对角,判断三角形是否有解,若有
解,请作出解答.
(1)a=10,b=20,A=80°;
(2)a=2?,b=6,A=30°.
解析 (1)a=10,b=20,a∵bsin
A=20sin
80°>20sin
60°=10?>10,
∴aA,∴该三角形无解.
(2)a=2?,b=6,a∵bsin
A=6sin
30°=3,∴a>bsin
A,
∴bsin
A由正弦定理得,sin
B=?=?=?,
∵B∈(0°,180°),∴B=60°或B=120°.
当B=60°时,C=90°,c=?=?=4?;
当B=120°时,C=30°,c=?=?=2?.
∴当B=60°时,C=90°,c=4?;
当B=120°时,C=30°,c=2?.
探究二 三角形的面积及应用
例2 (1)(易错题)在△ABC中,角A、B、C的对边分别是a、b、c,c=?,b=1,B=
30°,则△ABC的面积为?( )
A.? ????
B.?或?
C.
?或? ????D.
?
B
(2)在△ABC中,角A,B,C所对的边分别是a,b,c,m=(sin
A,sin
B),n=(cos
B,cos
A),m·
n=-sin
2C.
①求C的大小;
②若c=2?,A=?,求△ABC的面积.
解析 (1)∵在△ABC中,B=30°,b=1,c=?,
∴?=?,
∴sin
C=?,
∴C=60°或C=120°,
当C=60°时,A=90°,
S△ABC=?bcsin
A=?;
当C=120°时,A=30°,
S△ABC=?bcsin
A=?.
故选B.
(2)①由题意,知m·n=sin
Acos
B+sin
Bcos
A=-sin
2C,
即sin(A+B)=-sin
2C,
因为sin(A+B)=sin
C,
所以sin
C=-2sin
Ccos
C.
由0C>0.
所以cos
C=-?,
所以C=?.
②由C=?,A=?,
得B=π-A-C=?.
由?=?,
得?=?,
解得b=2.
所以△ABC的面积S=?bcsin
A=?×2×2?×sin
?=?.
变式训练
1.(变条件)将例2(2)中的条件“若c=2?,A=?”改为“若△ABC为等腰三角形
且c=2?”,求△ABC的面积.
解析 ∵△ABC为等腰三角形,
∴A=B=?,
由?=?,
得?=?,
解得b=2.
∴△ABC的面积S=?bcsin
A=?×2×2?×sin
?=?.
2.(变条件,变结论)将例2(2)中的条件“m=(sin
A,sin
B),n=(cos
B,cos
A),m·n=
-sin
2C”改为“a+c=2b,2cos
2B-8cos
B+5=0”,求角B的大小,并判断△ABC的形
状.
解析 ∵2cos
2B-8cos
B+5=0,
∴2(2cos2B-1)-8cos
B+5=0.
∴4cos2B-8cos
B+3=0,
即(2cos
B-1)(2cos
B-3)=0,
解得cos
B=?或cos
B=?(舍去).
∵0∴B=?.
∵a+c=2b,
∴由正弦定理,
得sin
A+sin
C=2sin
B=2sin
?=?.
∴sin
A+sin?=?,
∴sin
A+sin?cos
A-cos
?sin
A=?,
化简得?sin
A+?cos
A=?,
∴sin?=1.
∵0∴?∴A+?=?,
∴A=?,C=?,
∴△ABC是等边三角形.
易错点拨
求三角形的面积容易时出现漏解或多解的情况,注意判断三角形的解的个数,
避免漏解或多解.
跟踪训练
2-1 在△ABC中,角A、B、C的对边分别为a、b、c.已知cos
C=?.若?·?=?,
求△ABC的面积.
解析 由?·?=?,得abcos
C=?.
因为cos
C=?,所以ab=?=?.
又C为△ABC的内角,所以sin
C=?,
所以△ABC的面积S=?absin
C=3.
课堂检测
评价检测·素养提升
1.已知锐角△ABC的面积为3?,BC=4,CA=3,则角C的大小为?( )
A.75° ????B.60° ????C.45° ????D.30°
解析 由三角形的面积公式,得?BC·CA·sin
C=3?,即?×4×3sin
C=3?,解
得sin
C=?,因为△ABC为锐角三角形,所以C=60°.
B
2.在△ABC中,bsin
AA.无解 ????B.有两解
C.有一解 ????D.有无数解
解析 因为bsin
AA<1,Aasin
B=bsin
AB<1,
当A当90°故此三角形有两解.故选B.
B
3.设三角形的内角A,B,C所对的边分别为a,b,c,且C=?,a+b=12,则三角形面积的
最大值为?( )
A.6 ????B.8 ????C.7 ????D.9
解析 利用基本不等式可得a+b≥2?,当且仅当a=b=6时等号成立,即2
≤12,解得ab≤36,当且仅当a=b=6时等号成立,因为C=?,所以S△ABC=?absin
C
≤?×36×sin
?=9,当且仅当a=b=6时等号成立,故三角形面积的最大值为9.故
选D.
D
4.在锐角△ABC中,角A、B、C所对的边分别为a、b、c,若△ABC的面积为?,
且b=1,c=2,则∠A的大小为 ????.
解析 由三角形的面积公式可知,S△ABC=?bcsin
A=?×1×2×sin
A=?,解得sin
A=
?,因为△ABC为锐角三角形,所以∠A的大小为?.
5.如图,AD是△ABC外角的平分线,且BC=CD.
证明:?=?=?.
?
证明 由题设知S△ABD=2S△ACD,sin∠BAD
=sin(π-∠BAD)=sin∠CAD,
所以?=?=?=?=?.
逻辑推理——解三角形的规范解答
△ABC的内角A,B,C的对边分别为a,b,c,且a(?sin
B-cos
C)=(c-b)cos
A.
(1)求A;
(2)若b=?,点D在BC边上,CD=2,∠ADC=?,求△ABC的面积.
审:由正弦定理将边化成角,即可求得A的值.在△ADC中,由正弦定理可得
sin∠CAD的值,从而可求得∠CAD,利用三角形内角和定理可求得∠C,∠B,
即可求得AB=AC,再利用三角形的面积公式即可计算得解.
素养演练
联:在利用正弦定理后,联系三角恒等变换的知识点,进一步将问题细化到具体
的求角问题上,考查学生逻辑推理的素养以及利用公式进行数学运算的素养.
解:(1)∵a(?sin
B-cos
C)=(c-b)cos
A,
∴由正弦定理可得,?sin
Asin
B-sin
Acos
C=sin
Ccos
A-sin
Bcos
A,
即?sin
Asin
B+sin
Bcos
A=sin
Ccos
A+sin
Acos
C,
∴sin
B(?sin
A+cos
A)=sin
B,
∵sin
B>0,
∴?sin
A+cos
A=2sin?=1,
可得sin?=①?.
∵A∈(0,π),
∴A+?∈?,
∴A+?=②?,∴A=③?.
(2)∵b=?,点D在BC边上,CD=2,∠ADC=?,
∴在△ADC中,由?=?,可得?=?,∴sin∠CAD=④_____,
∴∠CAD=?,∴∠C=π-∠CAD-∠ADC=?,
∴∠B=π-∠BAC-∠C=?,
∴AB=AC=⑤?,
∴S△ABC=?AB·AC·sin∠BAC=?×?×?×?=⑥?.
1
思:本题主要考查了正弦定理、三角函数恒等变换的应用,三角形内角和定理
及三角形的面积公式在解三角形中的应用,考查了学生计算能力和转化能力.
针对训练
已知△ABC的内角A、B、C的对边分别为a、b、c,且A=?,a=?,b=?.
(1)求角B、C;
(2)求△ABC的面积.
解析 (1)∵A=?,a=?,b=?,
?=?,∴?=?,
解得sin
B=?.
∵B∈(0,π),
∴B=?或B=?,又∵a>b,∴B=?.
∴C=?.
(2)△ABC的面积S=?absin
C=?×?×?×sin
?=?×?=?.
第2课时 正弦定理的应用
第一篇
教材过关
情景导学
精读教材·必备知识
1.对三角形解的个数的判断
图形
关系式
解的个数
A为
锐角
?
(i)a=bsin
A;
(ii)a≥b
一解
?
bsin
A
?
①____________
无解
a
A为钝
角或
直角
?
a>b
一解
?
a≤b
无解
上表也可记为:
A为钝角
A为直角
A为锐角
a>b
一解
一解
一解
a=b
无解
无解
一解
a
无解
a>bsin
A
两解
a=bsin
A
一解
a
无解
特别提醒
已知三角形的两角和任意一边,求另两边和另一角,此时有唯一解,三角形被唯
一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两
解或无解的情况,三角形不能被唯一确定.
2.三角形的面积公式
任意三角形的面积公式为:
S△ABC=?bcsin
A=②_________=③__________.
即任意三角形的面积等于任意两边与它们夹角的正弦值的乘积的一半.
提示 ①S△ABC=?ah,其中a为△ABC的一边长,h为该边上的高.
②S△ABC=?r(a+b+c)=?rl,其中r,l分别为△ABC的内切圆半径及△ABC的周长.
思考:除了上面提到的三角形面积公式,你还能想到其他的三角形面积公式吗?
例1 (1)在△ABC中,角A,B,C的对边分别是a,b,c,已知a=2,B=45°,b=1,则满足条
件的三角形的个数为?( )
A.0 ????B.1
C.2 ????D.无数
(2)(多选)在△ABC中,角A,B,C的对边分别是a,b,c,根据下列条件解三角形,其中
有两解的是?( )
A.b=10,A=45°,C=70°
B.b=45,c=48,B=60°
C.a=14,b=16,A=45°
D.a=7,b=5,A=80°
A
BC
互动探究·关键能力
探究一 三角形解的个数的判断
解析 (1)由?=?,得sin
A=?>1,所以满足条件的三角形的个数是0.
故选A.
(2)选项B满足csin
60°
对于选项D,由sin
B=?,且b
思维突破
已知两边和其中一边的对角解三角形时,首先求出另一边的对角的正弦值,再
利用该正弦值求角,此时要根据已知两边的大小情况来确定该角有一个值还
是两个值,或者根据该正弦值(不等于1时)在0°~180°范围内求角,一个锐角,一
个钝角,只要不与三角形内角和定理矛盾,就是所求.
跟踪训练
1-1 已知下列各三角形中的两边及其一边的对角,判断三角形是否有解,若有
解,请作出解答.
(1)a=10,b=20,A=80°;
(2)a=2?,b=6,A=30°.
解析 (1)a=10,b=20,a
A=20sin
80°>20sin
60°=10?>10,
∴a
(2)a=2?,b=6,a
A=6sin
30°=3,∴a>bsin
A,
∴bsin
A
B=?=?=?,
∵B∈(0°,180°),∴B=60°或B=120°.
当B=60°时,C=90°,c=?=?=4?;
当B=120°时,C=30°,c=?=?=2?.
∴当B=60°时,C=90°,c=4?;
当B=120°时,C=30°,c=2?.
探究二 三角形的面积及应用
例2 (1)(易错题)在△ABC中,角A、B、C的对边分别是a、b、c,c=?,b=1,B=
30°,则△ABC的面积为?( )
A.? ????
B.?或?
C.
?或? ????D.
?
B
(2)在△ABC中,角A,B,C所对的边分别是a,b,c,m=(sin
A,sin
B),n=(cos
B,cos
A),m·
n=-sin
2C.
①求C的大小;
②若c=2?,A=?,求△ABC的面积.
解析 (1)∵在△ABC中,B=30°,b=1,c=?,
∴?=?,
∴sin
C=?,
∴C=60°或C=120°,
当C=60°时,A=90°,
S△ABC=?bcsin
A=?;
当C=120°时,A=30°,
S△ABC=?bcsin
A=?.
故选B.
(2)①由题意,知m·n=sin
Acos
B+sin
Bcos
A=-sin
2C,
即sin(A+B)=-sin
2C,
因为sin(A+B)=sin
C,
所以sin
C=-2sin
Ccos
C.
由0
所以cos
C=-?,
所以C=?.
②由C=?,A=?,
得B=π-A-C=?.
由?=?,
得?=?,
解得b=2.
所以△ABC的面积S=?bcsin
A=?×2×2?×sin
?=?.
变式训练
1.(变条件)将例2(2)中的条件“若c=2?,A=?”改为“若△ABC为等腰三角形
且c=2?”,求△ABC的面积.
解析 ∵△ABC为等腰三角形,
∴A=B=?,
由?=?,
得?=?,
解得b=2.
∴△ABC的面积S=?bcsin
A=?×2×2?×sin
?=?.
2.(变条件,变结论)将例2(2)中的条件“m=(sin
A,sin
B),n=(cos
B,cos
A),m·n=
-sin
2C”改为“a+c=2b,2cos
2B-8cos
B+5=0”,求角B的大小,并判断△ABC的形
状.
解析 ∵2cos
2B-8cos
B+5=0,
∴2(2cos2B-1)-8cos
B+5=0.
∴4cos2B-8cos
B+3=0,
即(2cos
B-1)(2cos
B-3)=0,
解得cos
B=?或cos
B=?(舍去).
∵0
∵a+c=2b,
∴由正弦定理,
得sin
A+sin
C=2sin
B=2sin
?=?.
∴sin
A+sin?=?,
∴sin
A+sin?cos
A-cos
?sin
A=?,
化简得?sin
A+?cos
A=?,
∴sin?=1.
∵0
∴A=?,C=?,
∴△ABC是等边三角形.
易错点拨
求三角形的面积容易时出现漏解或多解的情况,注意判断三角形的解的个数,
避免漏解或多解.
跟踪训练
2-1 在△ABC中,角A、B、C的对边分别为a、b、c.已知cos
C=?.若?·?=?,
求△ABC的面积.
解析 由?·?=?,得abcos
C=?.
因为cos
C=?,所以ab=?=?.
又C为△ABC的内角,所以sin
C=?,
所以△ABC的面积S=?absin
C=3.
课堂检测
评价检测·素养提升
1.已知锐角△ABC的面积为3?,BC=4,CA=3,则角C的大小为?( )
A.75° ????B.60° ????C.45° ????D.30°
解析 由三角形的面积公式,得?BC·CA·sin
C=3?,即?×4×3sin
C=3?,解
得sin
C=?,因为△ABC为锐角三角形,所以C=60°.
B
2.在△ABC中,bsin
A
C.有一解 ????D.有无数解
解析 因为bsin
A
B=bsin
A
当A
B
3.设三角形的内角A,B,C所对的边分别为a,b,c,且C=?,a+b=12,则三角形面积的
最大值为?( )
A.6 ????B.8 ????C.7 ????D.9
解析 利用基本不等式可得a+b≥2?,当且仅当a=b=6时等号成立,即2
≤12,解得ab≤36,当且仅当a=b=6时等号成立,因为C=?,所以S△ABC=?absin
C
≤?×36×sin
?=9,当且仅当a=b=6时等号成立,故三角形面积的最大值为9.故
选D.
D
4.在锐角△ABC中,角A、B、C所对的边分别为a、b、c,若△ABC的面积为?,
且b=1,c=2,则∠A的大小为 ????.
解析 由三角形的面积公式可知,S△ABC=?bcsin
A=?×1×2×sin
A=?,解得sin
A=
?,因为△ABC为锐角三角形,所以∠A的大小为?.
5.如图,AD是△ABC外角的平分线,且BC=CD.
证明:?=?=?.
?
证明 由题设知S△ABD=2S△ACD,sin∠BAD
=sin(π-∠BAD)=sin∠CAD,
所以?=?=?=?=?.
逻辑推理——解三角形的规范解答
△ABC的内角A,B,C的对边分别为a,b,c,且a(?sin
B-cos
C)=(c-b)cos
A.
(1)求A;
(2)若b=?,点D在BC边上,CD=2,∠ADC=?,求△ABC的面积.
审:由正弦定理将边化成角,即可求得A的值.在△ADC中,由正弦定理可得
sin∠CAD的值,从而可求得∠CAD,利用三角形内角和定理可求得∠C,∠B,
即可求得AB=AC,再利用三角形的面积公式即可计算得解.
素养演练
联:在利用正弦定理后,联系三角恒等变换的知识点,进一步将问题细化到具体
的求角问题上,考查学生逻辑推理的素养以及利用公式进行数学运算的素养.
解:(1)∵a(?sin
B-cos
C)=(c-b)cos
A,
∴由正弦定理可得,?sin
Asin
B-sin
Acos
C=sin
Ccos
A-sin
Bcos
A,
即?sin
Asin
B+sin
Bcos
A=sin
Ccos
A+sin
Acos
C,
∴sin
B(?sin
A+cos
A)=sin
B,
∵sin
B>0,
∴?sin
A+cos
A=2sin?=1,
可得sin?=①?.
∵A∈(0,π),
∴A+?∈?,
∴A+?=②?,∴A=③?.
(2)∵b=?,点D在BC边上,CD=2,∠ADC=?,
∴在△ADC中,由?=?,可得?=?,∴sin∠CAD=④_____,
∴∠CAD=?,∴∠C=π-∠CAD-∠ADC=?,
∴∠B=π-∠BAC-∠C=?,
∴AB=AC=⑤?,
∴S△ABC=?AB·AC·sin∠BAC=?×?×?×?=⑥?.
1
思:本题主要考查了正弦定理、三角函数恒等变换的应用,三角形内角和定理
及三角形的面积公式在解三角形中的应用,考查了学生计算能力和转化能力.
针对训练
已知△ABC的内角A、B、C的对边分别为a、b、c,且A=?,a=?,b=?.
(1)求角B、C;
(2)求△ABC的面积.
解析 (1)∵A=?,a=?,b=?,
?=?,∴?=?,
解得sin
B=?.
∵B∈(0,π),
∴B=?或B=?,又∵a>b,∴B=?.
∴C=?.
(2)△ABC的面积S=?absin
C=?×?×?×sin
?=?×?=?.
