人教B版(2019)高中数学必修第四册9.2正弦定理与余弦定理的应用课件(共35张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第四册9.2正弦定理与余弦定理的应用课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 774.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 21:14:14 | ||
图片预览









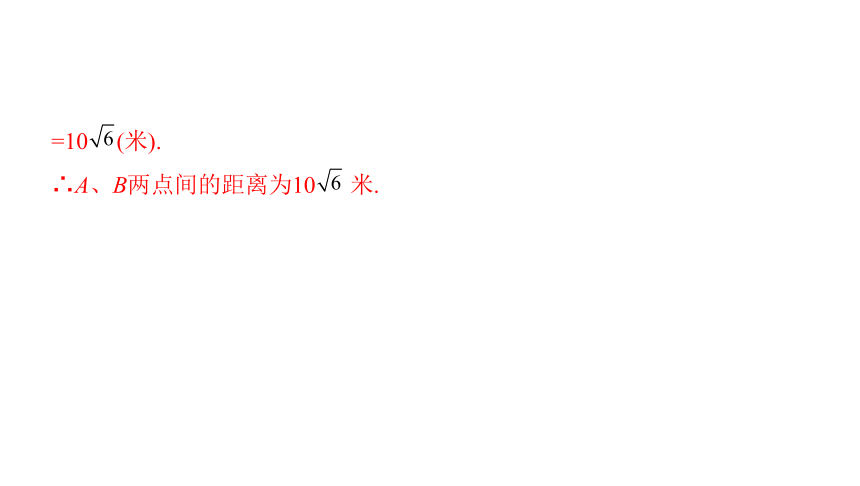
文档简介
(共35张PPT)
§9.2 正弦定理与余弦定理的应用
第一篇
教材过关
情景导学
精读教材·必备知识
我们都知道,月球是距离地球最近的星球,月球与地球近地点的距离是36.3万
千米,与地球远地点的距离是40.6万千米,地球与月球的平均距离是
384
403.9
千米.可以肯定的是,没有一个人测量过地月距离.
问题:你能给出一个方案,测量出地月距离吗?
答案 可以在地球上选两点,与月亮构成三角形,测量地球上两点的距离和从
这两点看月亮的视角,通过解三角形求得地月距离.
1.实际问题中的一些有关角的术语
(1)方向角:指正北或正南方向线与目标方向线所成的小于①______度的角.
思考:如图,图1表示北偏东②______,图2表示南偏西③______.
?
图1 图2
教材研读
90
30°
60°
(2)涉及高度的常用术语——仰角与俯角:
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水
平视线④_______时叫仰角,目标视线在水平视线⑤______时叫俯角.(如图所示)
?
上方
下方
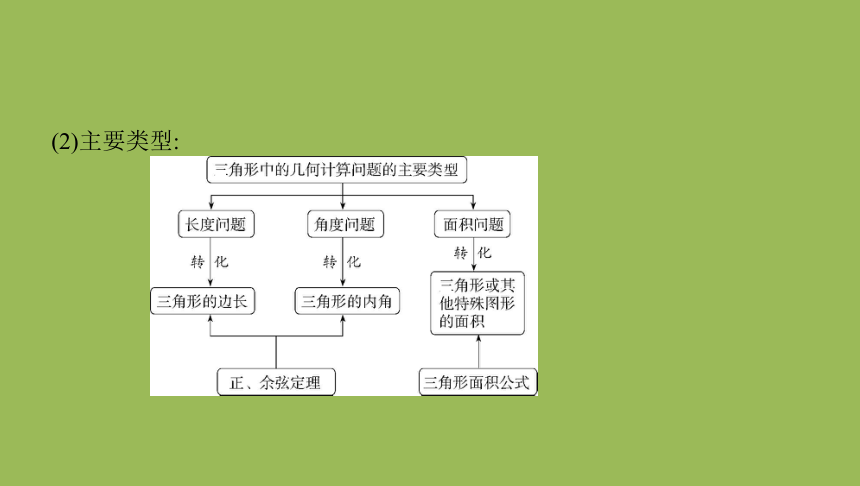
2.解三角形应用题(数学建模素养)
解三角形应用题时,通常都要根据题意从实际问题中抽象出一个或几个三角
形,然后通过解三角形得到实际问题的解,求解的关键是将实际问题转化为解
三角形问题.
(1)解题思路:
(2)主要类型:
互动探究·关键能力
探究一 测量距离问题
例1 海上A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C
岛和A岛成75°的视角,则B,C间的距离是 ????海里.
解析 如图所示.
?
在△ABC中,A=60°,B=75°,AB=10
海里,
∴C=45°.
由正弦定理可得?=?,
即?=?,∴BC=5?(海里).
思维突破
求距离问题时应注意的三点
(1)选定或确定所求量所在的三角形.若其他量已知,则直接解;若有未知量,则
把未知量放在另一个确定的三角形中求解.
(2)确定用正弦定理还是余弦定理.如果都可用,那么就选择更便于计算的定理.
(3)测量两个不可到达的点之间的距离时,首先把测量不可到达的两点A,B之间
的距离问题转化为应用余弦定理求三角形的边长问题,然后在相关三角形中
利用正弦定理计算相关的边长.
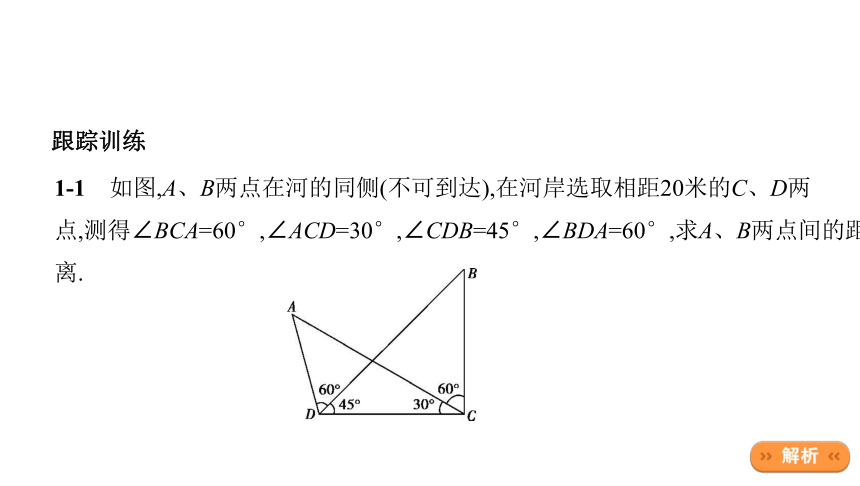
跟踪训练
1-1 如图,A、B两点在河的同侧(不可到达),在河岸选取相距20米的C、D两
点,测得∠BCA=60°,∠ACD=30°,∠CDB=45°,∠BDA=60°,求A、B两点间的距
离.
?
解析 在△ADC中,由正弦定理得AC=?
?
=10(1+?)(米),
BC=?=20(米),
连接AB,
在△ABC中,由余弦定理得,
AB=?
=10?(米).
∴A、B两点间的距离为10?
米.
探究二 测量高度问题
例2 如图所示,A、B是水平面上相距800
m的两个点,在A点测得山顶C的仰角
为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中D点是点C到水平面的垂足,
求山高CD.
?
解析 易知CD⊥AD,∠CAD=45°,所以CD=AD.
因此只需在△ABD中求出AD即可.
在△ABD中,∠BDA=180°-45°-120°=15°,
由?
得?=?
=800(?+1)
m.
所以山高CD为800(?+1)
m.
跟踪训练
2-1 如图,某中学数学兴趣小组要测量底部不能到达的某铁塔AB的高度(如
图),铁塔AB垂直于水平面,在塔的同一侧且与塔底部B在同一水平面上选择C,
D两观测点,且在C,D两点测得塔顶的仰角分别为45°,30°,并测得∠BCD=120°,
C,D两地相距600
m,则铁塔AB的高度是?( )
?
B
A.300
m B.600
m
C.300?
m D.600?
m
解析 设AB=x
m,由已知可得BC=AB=x
m,BD=?x
m,
在△BCD中,由余弦定理可得3x2=x2+6002-2×600xcos
120°,
整理得x2-300x-180
000=0,
解得x=600(舍负).
故选B.
探究三 测量角度问题
例3 如图,在海岸A处发现北偏东45°方向,且距A处(?-1)海里的B处有一艘走
私船.在A处北偏西75°方向,且距A处2海里的C处,我方缉私船正奉命以10?
海
里/时的速度追截走私船,此时走私船正以10海里/时的速度从B处向北偏东30°
方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
?
解析 设缉私船沿CD方向行驶t小时,才能最快截获(在D点)走私船,则CD=
10?t
海里,BD=10t
海里,
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·ACcos∠CAB=(?-1)2+22-2(?-
1)×2×cos
120°=6,∴BC=?
海里.∵?=?,
∴sin∠ABC=?=?=?,
又∠ABC∈(0°,60°),
∴∠ABC=45°,
∴B点在C点的正东方向上,
∴∠CBD=90°+30°=120°,
在△BCD中,由正弦定理得?=?,
∴sin∠BCD=?
=?=?.
又∵∠BCD∈(0°,90°),∴∠BCD=30°,
∴缉私船应沿北偏东60°的方向行驶.
又在△BCD中,∠CBD=120°,∠BCD=30°,
∴∠D=30°,∴BD=BC=10t=?
海里.∴t=?小时≈15分钟.
∴缉私船沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
思维突破
测量角度问题画示意图的基本步骤
?
跟踪训练
3-1 如图,一轮船从A点沿北偏东70°的方向行驶10海里至海岛B,又从B沿北偏
东10°的方向行驶10海里至海岛C,若此轮船从A点直接沿直线行驶至海岛C,则
此船沿 ????方向行驶 ????海里至海岛C?( )
?
B
A.北偏东60°;10?
B.北偏东40°;10?
C.北偏东30°;10?
D.北偏东20°;10?
解析 因为AB=BC,所以∠BAC=∠C=?=30°,AC2=AB2+BC2-2AB·BC-
cos∠ABC=300,所以AC=10?
海里,所以此船沿北偏东40°方向行驶10?海里
至海岛C.
课堂检测
评价检测·素养提升
1.两座灯塔A和B与海洋观察站C的距离分别为3
km,5
km,灯塔A在观察站C的
北偏东20°方向上,灯塔B在观察站C的南偏东40°方向上,则灯塔A与B的距离为
?( )
A.6
km B.4?
km
C.7
km D.5?
km
解析 由题意可得∠ACB=120°,∴AB2=9+25-2×3×5×cos
120°=49,∴AB=7
km.
C
2.(2020山东模拟)泉城广场上矗立着的“泉标”成为了济南的标志和象征.为
了测量“泉标”的高度,某同学在“泉标”的正西方向的点A处测得“泉标”
顶端的仰角为45°,沿点A向北偏东30°方向前进100
m到达点B,在点B处测得
“泉标”顶端的仰角为30°,则“泉标”的高度为?( )
A.50
m B.100
m
C.120
m D.150
m
A
解析 根据题意,画图如下,
?
则AB=100
m,∠BAC=60°,∠DBC=30°,设DC=x
m,
则AC=x
m,BC=?x
m,
在△ABC中,
由余弦定理,得
(?x)2=x2+1002-2×x×100×?,
解得x=50(舍负).
故选A.
3.如图,为测量一棵树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖
的仰角为30°,45°,且A,B两点之间的距离为60
m,则树的高度为?( )
?
A.(30+30?)m
B.(30+15?)m
C.(15+30?)m
D.(15+3?)m
A
解析 在△PAB中,∠PAB=30°,
∠APB=15°,AB=60
m,
sin
15°=sin(45°-30°)
=sin
45°cos
30°-cos
45°·sin
30°
=?×?-?×?=?,
由正弦定理得
?
∴PB=?=30(?+?)
m,
PB·sin
45°=(30+30?)
m,
∴树的高度为(30+30?)
m.
数学建模——方案设计问题
如图,要测量山顶上的电视塔FG的高度,已知山的西面有一栋楼AC(该楼的高
度低于山的高度).试设计在楼AC上测量并计算山顶上的电视塔高度的方案.
素养演练
解:设在楼顶C看塔顶、塔底的仰角分别是α、β,从楼顶下的B点看塔底的仰角
为γ,测出BC=h.如图,
在△BCF中,BC=h,∠CBF=?-γ,∠BCF=?+β,∠BFC=γ-β.由正弦定理,得
?=?,即?=?,所以BF=?.
在Rt△BEF中,有BE=BFcos
γ=?.
在Rt△CGM中,CM=BE,∠GCM=α,则MG=①???
在Rt△CFM中,CM=BE,∠FCM=β,则MF=CMtan
β=②??.
则电视塔的高度FG=③_____________________________.
素养探究:数学建模中方案设计的一般思路:
(1)分析:理解题意,分清已知与未知,画出示意图;
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角
形中,建立一个解三角形的数学模型;
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;
(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.
针对训练
某中学校园内有一个“湖泊”,湖的两侧有一个音乐教室和一个图书馆,如
图,若音乐教室设在A处,图书馆设在B处,为测量A,B两地之间的距离,某同学选
定了与A,B不共线的C处,构成△ABC,以下是几种不同的测量方案:①测量∠A,
AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B.其中一定能
唯一确定A,B两地之间的距离的所有方案的序号是 ????.
?
②③
解析 ①测量∠A,AC,BC,已知两边及其中一边的对角,由正弦定理可知,三角
形可能有两个解,不能唯一确定点A,B两地之间的距离;
②测量∠A,∠B,BC,已知两角及其中一角的对边,由正、余弦定理可知,三角形
有唯一的解,能唯一确定点A,B两地之间的距离;
③测量∠C,AC,BC,已知两边及其夹角,由余弦定理可知,三角形有唯一的解,能
唯一确定点A,B两地之间的距离;
④测量∠A,∠C,∠B,知道三个角度值,三角形有无数多组解,不能唯一确定点A,
B两地之间的距离.综上,一定能唯一确定A,B两地之间的距离的所有方案的序号
是②③.
§9.2 正弦定理与余弦定理的应用
第一篇
教材过关
情景导学
精读教材·必备知识
我们都知道,月球是距离地球最近的星球,月球与地球近地点的距离是36.3万
千米,与地球远地点的距离是40.6万千米,地球与月球的平均距离是
384
403.9
千米.可以肯定的是,没有一个人测量过地月距离.
问题:你能给出一个方案,测量出地月距离吗?
答案 可以在地球上选两点,与月亮构成三角形,测量地球上两点的距离和从
这两点看月亮的视角,通过解三角形求得地月距离.
1.实际问题中的一些有关角的术语
(1)方向角:指正北或正南方向线与目标方向线所成的小于①______度的角.
思考:如图,图1表示北偏东②______,图2表示南偏西③______.
?
图1 图2
教材研读
90
30°
60°
(2)涉及高度的常用术语——仰角与俯角:
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水
平视线④_______时叫仰角,目标视线在水平视线⑤______时叫俯角.(如图所示)
?
上方
下方
2.解三角形应用题(数学建模素养)
解三角形应用题时,通常都要根据题意从实际问题中抽象出一个或几个三角
形,然后通过解三角形得到实际问题的解,求解的关键是将实际问题转化为解
三角形问题.
(1)解题思路:
(2)主要类型:
互动探究·关键能力
探究一 测量距离问题
例1 海上A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C
岛和A岛成75°的视角,则B,C间的距离是 ????海里.
解析 如图所示.
?
在△ABC中,A=60°,B=75°,AB=10
海里,
∴C=45°.
由正弦定理可得?=?,
即?=?,∴BC=5?(海里).
思维突破
求距离问题时应注意的三点
(1)选定或确定所求量所在的三角形.若其他量已知,则直接解;若有未知量,则
把未知量放在另一个确定的三角形中求解.
(2)确定用正弦定理还是余弦定理.如果都可用,那么就选择更便于计算的定理.
(3)测量两个不可到达的点之间的距离时,首先把测量不可到达的两点A,B之间
的距离问题转化为应用余弦定理求三角形的边长问题,然后在相关三角形中
利用正弦定理计算相关的边长.
跟踪训练
1-1 如图,A、B两点在河的同侧(不可到达),在河岸选取相距20米的C、D两
点,测得∠BCA=60°,∠ACD=30°,∠CDB=45°,∠BDA=60°,求A、B两点间的距
离.
?
解析 在△ADC中,由正弦定理得AC=?
?
=10(1+?)(米),
BC=?=20(米),
连接AB,
在△ABC中,由余弦定理得,
AB=?
=10?(米).
∴A、B两点间的距离为10?
米.
探究二 测量高度问题
例2 如图所示,A、B是水平面上相距800
m的两个点,在A点测得山顶C的仰角
为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中D点是点C到水平面的垂足,
求山高CD.
?
解析 易知CD⊥AD,∠CAD=45°,所以CD=AD.
因此只需在△ABD中求出AD即可.
在△ABD中,∠BDA=180°-45°-120°=15°,
由?
得?=?
=800(?+1)
m.
所以山高CD为800(?+1)
m.
跟踪训练
2-1 如图,某中学数学兴趣小组要测量底部不能到达的某铁塔AB的高度(如
图),铁塔AB垂直于水平面,在塔的同一侧且与塔底部B在同一水平面上选择C,
D两观测点,且在C,D两点测得塔顶的仰角分别为45°,30°,并测得∠BCD=120°,
C,D两地相距600
m,则铁塔AB的高度是?( )
?
B
A.300
m B.600
m
C.300?
m D.600?
m
解析 设AB=x
m,由已知可得BC=AB=x
m,BD=?x
m,
在△BCD中,由余弦定理可得3x2=x2+6002-2×600xcos
120°,
整理得x2-300x-180
000=0,
解得x=600(舍负).
故选B.
探究三 测量角度问题
例3 如图,在海岸A处发现北偏东45°方向,且距A处(?-1)海里的B处有一艘走
私船.在A处北偏西75°方向,且距A处2海里的C处,我方缉私船正奉命以10?
海
里/时的速度追截走私船,此时走私船正以10海里/时的速度从B处向北偏东30°
方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
?
解析 设缉私船沿CD方向行驶t小时,才能最快截获(在D点)走私船,则CD=
10?t
海里,BD=10t
海里,
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·ACcos∠CAB=(?-1)2+22-2(?-
1)×2×cos
120°=6,∴BC=?
海里.∵?=?,
∴sin∠ABC=?=?=?,
又∠ABC∈(0°,60°),
∴∠ABC=45°,
∴B点在C点的正东方向上,
∴∠CBD=90°+30°=120°,
在△BCD中,由正弦定理得?=?,
∴sin∠BCD=?
=?=?.
又∵∠BCD∈(0°,90°),∴∠BCD=30°,
∴缉私船应沿北偏东60°的方向行驶.
又在△BCD中,∠CBD=120°,∠BCD=30°,
∴∠D=30°,∴BD=BC=10t=?
海里.∴t=?小时≈15分钟.
∴缉私船沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
思维突破
测量角度问题画示意图的基本步骤
?
跟踪训练
3-1 如图,一轮船从A点沿北偏东70°的方向行驶10海里至海岛B,又从B沿北偏
东10°的方向行驶10海里至海岛C,若此轮船从A点直接沿直线行驶至海岛C,则
此船沿 ????方向行驶 ????海里至海岛C?( )
?
B
A.北偏东60°;10?
B.北偏东40°;10?
C.北偏东30°;10?
D.北偏东20°;10?
解析 因为AB=BC,所以∠BAC=∠C=?=30°,AC2=AB2+BC2-2AB·BC-
cos∠ABC=300,所以AC=10?
海里,所以此船沿北偏东40°方向行驶10?海里
至海岛C.
课堂检测
评价检测·素养提升
1.两座灯塔A和B与海洋观察站C的距离分别为3
km,5
km,灯塔A在观察站C的
北偏东20°方向上,灯塔B在观察站C的南偏东40°方向上,则灯塔A与B的距离为
?( )
A.6
km B.4?
km
C.7
km D.5?
km
解析 由题意可得∠ACB=120°,∴AB2=9+25-2×3×5×cos
120°=49,∴AB=7
km.
C
2.(2020山东模拟)泉城广场上矗立着的“泉标”成为了济南的标志和象征.为
了测量“泉标”的高度,某同学在“泉标”的正西方向的点A处测得“泉标”
顶端的仰角为45°,沿点A向北偏东30°方向前进100
m到达点B,在点B处测得
“泉标”顶端的仰角为30°,则“泉标”的高度为?( )
A.50
m B.100
m
C.120
m D.150
m
A
解析 根据题意,画图如下,
?
则AB=100
m,∠BAC=60°,∠DBC=30°,设DC=x
m,
则AC=x
m,BC=?x
m,
在△ABC中,
由余弦定理,得
(?x)2=x2+1002-2×x×100×?,
解得x=50(舍负).
故选A.
3.如图,为测量一棵树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖
的仰角为30°,45°,且A,B两点之间的距离为60
m,则树的高度为?( )
?
A.(30+30?)m
B.(30+15?)m
C.(15+30?)m
D.(15+3?)m
A
解析 在△PAB中,∠PAB=30°,
∠APB=15°,AB=60
m,
sin
15°=sin(45°-30°)
=sin
45°cos
30°-cos
45°·sin
30°
=?×?-?×?=?,
由正弦定理得
?
∴PB=?=30(?+?)
m,
PB·sin
45°=(30+30?)
m,
∴树的高度为(30+30?)
m.
数学建模——方案设计问题
如图,要测量山顶上的电视塔FG的高度,已知山的西面有一栋楼AC(该楼的高
度低于山的高度).试设计在楼AC上测量并计算山顶上的电视塔高度的方案.
素养演练
解:设在楼顶C看塔顶、塔底的仰角分别是α、β,从楼顶下的B点看塔底的仰角
为γ,测出BC=h.如图,
在△BCF中,BC=h,∠CBF=?-γ,∠BCF=?+β,∠BFC=γ-β.由正弦定理,得
?=?,即?=?,所以BF=?.
在Rt△BEF中,有BE=BFcos
γ=?.
在Rt△CGM中,CM=BE,∠GCM=α,则MG=①???
在Rt△CFM中,CM=BE,∠FCM=β,则MF=CMtan
β=②??.
则电视塔的高度FG=③_____________________________.
素养探究:数学建模中方案设计的一般思路:
(1)分析:理解题意,分清已知与未知,画出示意图;
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角
形中,建立一个解三角形的数学模型;
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;
(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.
针对训练
某中学校园内有一个“湖泊”,湖的两侧有一个音乐教室和一个图书馆,如
图,若音乐教室设在A处,图书馆设在B处,为测量A,B两地之间的距离,某同学选
定了与A,B不共线的C处,构成△ABC,以下是几种不同的测量方案:①测量∠A,
AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B.其中一定能
唯一确定A,B两地之间的距离的所有方案的序号是 ????.
?
②③
解析 ①测量∠A,AC,BC,已知两边及其中一边的对角,由正弦定理可知,三角
形可能有两个解,不能唯一确定点A,B两地之间的距离;
②测量∠A,∠B,BC,已知两角及其中一角的对边,由正、余弦定理可知,三角形
有唯一的解,能唯一确定点A,B两地之间的距离;
③测量∠C,AC,BC,已知两边及其夹角,由余弦定理可知,三角形有唯一的解,能
唯一确定点A,B两地之间的距离;
④测量∠A,∠C,∠B,知道三个角度值,三角形有无数多组解,不能唯一确定点A,
B两地之间的距离.综上,一定能唯一确定A,B两地之间的距离的所有方案的序号
是②③.
