2012高考冲刺平面向量篇

第六部分——平面向量
知识点总结精华
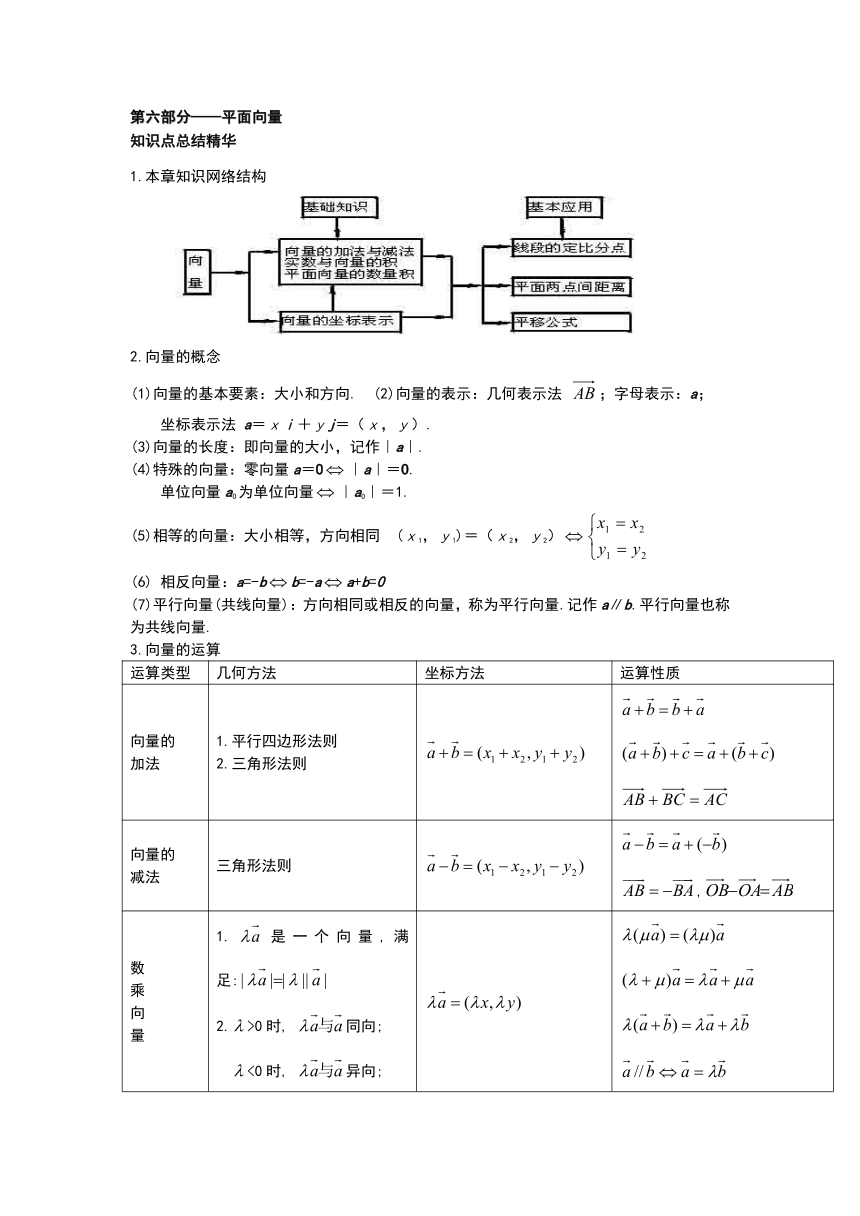
1.本章知识网络结构
?
2.向量的概念?
(1)向量的基本要素：大小和方向.?(2)向量的表示：几何表示法 ；字母表示：a；
坐标表示法 a＝ｘｉ＋ｙj＝（ｘ，ｙ）.?
(3)向量的长度：即向量的大小，记作｜a｜.?
(4)特殊的向量：零向量a＝O｜a｜＝O.?
单位向量aO为单位向量｜aO｜＝1.?
(5)相等的向量：大小相等，方向相同?(ｘ1，ｙ1)＝（ｘ2，ｙ2）
(6) 相反向量：a=-bb=-aa+b=0
(7)平行向量(共线向量)：方向相同或相反的向量，称为平行向量.记作a∥b.平行向量也称为共线向量.?
3.向量的运算?
运算类型 几何方法 坐标方法 运算性质
向量的加法 1.平行四边形法则2.三角形法则
向量的减法 三角形法则 ,
数乘向量 1.是一个向量,满足:2.>0时, 同向;<0时, 异向;=0时, .
向量的数量积 是一个数1.时，.2.
4.重要定理、公式
(1)平面向量基本定理?
e1，e2是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数λ1，
λ2，使a＝λ1e1＋λ2e2.?
(2)两个向量平行的充要条件?
a∥ba＝λb(b≠0)x1y2－x2y1＝O.?
(3)两个向量垂直的充要条件?
a⊥ba·b＝Ox1x2＋y1y 2＝O.?
(4)线段的定比分点公式?
设点P分有向线段所成的比为λ，即＝λ，则?
＝＋ (线段的定比分点的向量公式)?
(线段定比分点的坐标公式)?
当λ＝1时，得中点公式：?
＝（＋）或
(5)平移公式
设点P(x，y)按向量a＝（ｈ，ｋ）平移后得到点P′（x′，y′），
则＝+a或
曲线y＝f（x）按向量a＝（ｈ，ｋ）平移后所得的曲线的函数解析式为：
y－ｋ＝f（x－ｈ)
(6)正、余弦定理?
正弦定理：
余弦定理：a2＝b2＋c2－2bccosA，?
b2＝c2＋a2－2cacosB，?
c2＝a2＋b2－2abcosC.?
（7）三角形面积计算公式：
设△ABC的三边为a，b，c，其高分别为ha，hb，hc，半周长为P，外接圆、内切圆的半径为R，r.
①S△=1/2aha=1/2bhb=1/2chc ②S△=Pr ③S△=abc/4R
④S△=1/2sinC·ab=1/2ac·sinB=1/2cb·sinA ⑤S△= [海伦公式]
⑥S△=1/2（b+c-a）ra[如下图]=1/2（b+a-c）rc=1/2（a+c-b）rb
[注]：到三角形三边的距离相等的点有4个，一个是内心，其余3个是旁心.
如图：
图1中的I为S△ABC的内心， S△=Pr
图2中的I为S△ABC的一个旁心，S△=1/2（b+c-a）ra
附：三角形的五个“心”；
重心：三角形三条中线交点.
外心：三角形三边垂直平分线相交于一点.
内心：三角形三内角的平分线相交于一点.
垂心：三角形三边上的高相交于一点.
旁心：三角形一内角的平分线与另两条内角的外角平分线相交一点.
⑸已知⊙O是△ABC的内切圆，若BC=a，AC=b，AB=c [注：s为△ABC的半周长,即]
则：①AE==1/2（b+c-a）
②BN==1/2（a+c-b）
③FC==1/2（a+b-c）
综合上述：由已知得，一个角的邻边的切线长，等于半周长减去对边（如图4）.
特例：已知在Rt△ABC，c为斜边，则内切圆半径r=（如图3）.
⑹在△ABC中，有下列等式成立.
证明：因为所以，所以，结论！
⑺在△ABC中，D是BC上任意一点，则.
证明：在△ABCD中，由余弦定理，有①
在△ABC中，由余弦定理有②，②代入①，化简
可得，（斯德瓦定理）
①若AD是BC上的中线，；
②若AD是∠A的平分线，，其中为半周长；
③若AD是BC上的高，，其中为半周长.
⑻△ABC的判定：
△ABC为直角△∠A + ∠B =
＜△ABC为钝角△∠A + ∠B＜
＞△ABC为锐角△∠A + ∠B＞
附：证明：，得在钝角△ABC中，
⑼平行四边形对角线定理：对角线的平方和等于四边的平方和.
空间向量
1．空间向量的概念：
具有大小和方向的量叫做向量
注：⑴空间的一个平移就是一个向量
⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量
⑶空间的两个向量可用同一平面内的两条有向线段来表示
2．空间向量的运算
定义：与平面向量运算一样，空间向量的加法、减法与数乘向量运算如下
运算律：⑴加法交换律：
⑵加法结合律：
⑶数乘分配律：
3 共线向量
表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量．平行于记作．
当我们说向量、共线（或//）时，表示、的有向线段所在的直线可能是同一直线，也可能是平行直线．
4．共线向量定理及其推论：
共线向量定理：空间任意两个向量、（≠），//的充要条件是存在实数λ，使＝λ.
推论：如果为经过已知点A且平行于已知非零向量的直线，那么对于任意一点O，点P在直线上的充要条件是存在实数t满足等式
．
其中向量叫做直线的方向向量.
5．向量与平面平行：
已知平面和向量，作，如果直线平行于或在内，那么我们说向量平行于平面，记作：．
通常我们把平行于同一平面的向量，叫做共面向量
说明：空间任意的两向量都是共面的
6．共面向量定理：
如果两个向量不共线，与向量共面的充要条件是存在实数使
推论：空间一点位于平面内的充分必要条件是存在有序实数对，使或对空间任一点，有 ①
①式叫做平面的向量表达式
7 空间向量基本定理：
如果三个向量不共面，那么对空间任一向量，存在一个唯一的有序实数组，使
推论：设是不共面的四点，则对空间任一点，都存在唯一的三个
有序实数，使
8 空间向量的夹角及其表示：
已知两非零向量，在空间任取一点，作，则叫做向量与的夹角，记作；且规定，显然有；若，则称与互相垂直，记作：.
9．向量的模：
设，则有向线段的长度叫做向量的长度或模，记作：.
10．向量的数量积： ．
已知向量和轴，是上与同方向的单位向量，作点在上的射影，作点在上的射影，则叫做向量在轴上或在上的正射影.
可以证明的长度．
11．空间向量数量积的性质：
（1）．（2）．（3）．
12．空间向量数量积运算律：
（1）．（2）（交换律）（3）（分配律）．
空间向量的坐标运算
一．知识回顾：
（1）空间向量的坐标：空间直角坐标系的x轴是横轴（对应为横坐标），y轴是纵轴（对应为纵轴），z轴是竖轴（对应为竖坐标）.
①令=(a1,a2,a3),，则
∥
(用到常用的向量模与向量之间的转化：)
②空间两点的距离公式：.
（2）法向量：若向量所在直线垂直于平面，则称这个向量垂直于平面，记作，如果那么向量叫做平面的法向量.
（3）用向量的常用方法：
①利用法向量求点到面的距离定理：如图，设n是平面的法向量，AB是平面的一条射线，其中，则点B到平面的距离为.
②利用法向量求二面角的平面角定理：设分别是二面角中平面的法向量，则所成的角就是所求二面角的平面角或其补角大小（方向相同，则为补角，反方，则为其夹角）.
③证直线和平面平行定理：已知直线平面，，且CDE三点不共线，则a∥的充要条件是存在有序实数对使.（常设求解若存在即证毕，若不存在，则直线AB与平面相交）.
内心是三条角平分线的交点，它到三边的距离相等。
外心是三条边垂直平分线的交点，它到三个顶点的距离相等。 （是充要条件）
重心是三条中线的交点，它到顶点的距离是它到对边中点距离的2倍。
垂心是三条高的交点，它能构成很多直角三角形相似。
与三角形的“四心”有关的一些常见的重要的向量关系式有：
设，则向量必平分∠BAC，该向量必通过△ABC的内心;
设，则向量必平分∠BAC的邻补角
设，则向量必垂直于边BC，该向量必通过△ABC的垂心
△ABC中一定过的中点，通过△ABC的重心
点是△ABC的外心
点是△ABC的重心
点是△ABC的垂心
点是△ABC的内心 (其中a、b、c为△ABC三边)
△ABC的外心、重心、垂心共线，即∥
设为△ABC所在平面内任意一点，G为△ABC的重心，，I为△ABC的内心，
则有
并且重心G（，） 内心I（，）
试题精粹
江苏省2011年高考数学联考试题
10．（江苏天一中学、海门中学、盐城中学2011届高三调研考试）在中，，是内一点，且满足，则= ▲ ．（-3）
7．（江苏省2010届苏北四市第一次联考）在△ABC中，分别为三个内角A，B，C的对边，设向量，，若⊥，则角A的大小为 ▲ ．
10．（江苏省2010届苏北四市第一次联考）已知，其中，若，则的值等于 ▲ ．1
11、（南通市六所省重点高中联考试卷）在△ABC中，，D是BC边上任意一点（D与B、C不重合），
且，则等于 ▲
11. （苏北四市2011届高三第一次调研考试）在△ABC中，点M满足，若 ，则实数m的值为 ▲ ．
讲评建议：一种思维是对已知向量向目标向量分解，一种思维是理解已知向量条件的几何意义，既点M是三角形ABC的重心，再结合，三角形向量的中线形式，此问题观察即可解决，所以掌握相关结论，有了结论便利于联想。
6．（苏州市2011届高三调研测试）设分别是的斜边上的两个三等分点，已知,则 ▲ .
【解析】
16．（淮阴中学、姜堰中学、前黄中学2011届第一次联考）（14分）已知向量, ,
（1）若为中点，，求．的值；
（2）若是直角三角形，求的值。
16．解：(1) ∵ （1分）
而 ∴， （7分）
（2）①当时， ∴ （9分）
②当时，∵ （10分）
∴ ∴ （12分）
③当时，，∴
综上 或 （14分）
16、（南通市六所省重点高中联考试卷）（本题满分14分）已知向量，，，
其中、、为的内角.
(Ⅰ)求角的大小；
(Ⅱ)若，，成等差数列，且，求的长.
解：(Ⅰ) ………………………(2分)
对于，
………………………(4分)
又， ………………………(7分)
(Ⅱ)由，
由正弦定理得 ………………………(9分)
，
即 ……………………(12分)
由余弦弦定理，
， …………………(14分)
16．（无锡市1月期末调研）(本小题满分14分)
已知△ABC中，,,,．
（1）求；
（2）设，且已知 ，，求sinx．
16．（1）由已知，即，
∵ ∴，………………………………………………………………2分
∵， ∴， ………………………………………………………3分
在Rt△BCD 中，,
又, ∴， …………………………5分
∴． …………………………………………………………………6分
（2）在△ABC中，， ∴． ……………………………………………7分
即， ， ……………………………………9分
而， …………………………………………………………10分
则， ………………………………………………12分
∴，∴ ． ……………………………………14分
１．（无锡市1月期末调研）已知，点M在直线OC上运动，当取最小时，求点M的坐标．
1．设，…………………………………………………………………………2分
　　∴， ……………………………………………………………3分
， ……………………………………………………………4分
∴ ………………………………………6分
， …………………………………………………………………………8分
∴当时，最小．此时． ………………………………………………10分
16．（徐州市12月高三调研）(本小题满分14分)
设的三个内角所对的边分别为，且满足.
（Ⅰ）求角的大小；
（Ⅱ）若，试求的最小值.
16．解：（Ⅰ）因为，所以，
即，则 …………4分
所以，即，所以………………8分
（Ⅱ）因为，所以，即…12分
所以=，即的最小值为………………14分
试题精粹
江苏省2010年高考数学联考试题
一、填空题:
13．（江苏省南通市2010年高三二模）如图正六边形ABCDEF中，P是△CDE内(包括边界)的动点，设（α、β∈R），则α+β的取值范围是 ▲ ．
1．（江苏省无锡市2010年普通高中高三质量调研）已知向量=（1，1）与向量=（，）垂直，则= 。
解析：由与垂直得
12．（江苏省无锡市部分学校2010年4月联考试卷）已知是的内心，若，则 。
答案：
解析：此题用到平几中的角平分线定理，如不清楚此定理，较难做对。
13．（江苏省泰州市2010届高三联考试题）等腰直角三角形中，，，是边上的高，为的中点，点分别为边和边上的点，且关于直线对称，当时，______▲_______．
2. (江苏通州市2010年3月高三素质检测)已知向量和向量的夹角为，，则向量和向量的数量积= ▲。 ( http: / / www. )3
13．(江苏通州市2010年3月高三素质检测)如图，在等腰直角三角形ABC中，AC＝BC＝1，点M，N分别是AB，BC的中点，点P是△ABC（包括边界）内任一点．则的取值范围为
▲ ．高考资源网
（2010年3月苏、锡、常、镇四市高三教学情况调查一）已知两个单位向量,的夹角为，若向量，，则= ▲ ． 0
4．（江苏省盐城市2010年高三第二次调研考试）已知向量，若，则实数= ▲ .-1
6、（江苏省连云港市2010届高三二模试题）已知A（－3，0），B（0，），O为坐标原点，点C在第二象限，且∠AOC＝60°，＝λ＋，则实数λ的值是 ▲ ．
11．（江苏省苏南六校2010年高三年级联合调研考试）在中，已知D是AB边上一点，若，，则_____________．
3. （2010年江苏省苏北四市高三年级第二次模拟考试）已知向量，，若∥，则实数等于 ▲ .
12. （2010年江苏省苏北四市高三年级第二次模拟考试）如图，在平面四边形中，若， 则 ▲ .5
9、（江苏省南京市2010年3月高三第二次模拟）若平面向量a,b满足｛a+b｝=1,a+b平行于y轴，a=(2,-1),则b= 。（-2，2）或（-2，0）
10．（江苏省洪泽中学2010年4月高三年级第三次月考试卷）已知是平面上不共线三点，设为线段垂直平分线上任意一点，若，，则的值为 .12
二、解答题
15．（江苏省无锡市2010年普通高中高三质量调研）（本题满分14分）
如图，在△OAB中，已知P为线段AB上的一点，
（1）若，求，的值；
（2）若，，，且与的夹角为60°时，求 的值。
解析：
（1）∵，
∴，即， 3分
∴，即， 5分
（2）∵，
∴，即 7分
∴ 8分
∴， 9分
10分
12分
14分
16．（江苏省苏南六校2010年高三年级联合调研考试）（本小题满分14分）
在平行四边形中，设，，已知，
，其中；
（1）求的值；（2）求的值。
平面向量与解析几何解题方法
在高中数学新课程教材中，学生学习平面向量在前，学习解析几何在后，而且教材中二者知识整合的不多，很多学生在学习中就“平面向量”解平面向量题，不会应用平面向量去解决解析几何问题。用向量法解决解析几何问题思路清晰，过程简洁，有意想不到的神奇效果。著名教育家布鲁纳说过：学习的最好刺激是对所学材料的兴趣，简单的重复将会引起学生大脑疲劳，学习兴趣衰退。这充分揭示方法求变的重要性，如果我们能重视向量的教学，必然能引导学生拓展思路，减轻负担。
一、知识整合
平面向量是高中数学的新增内容，也是新高考的一个亮点。 向量知识、向量观点在数学、物理等学科的很多分支有着广泛的应用，它具有代数形式和几何形式的“双重身份”，能融数形与一体，能与中学数学教学内容的的许多主干知识综合，形成知识交汇点。而在高中数学体系中，解析几何占有着很重要的地位，有些问题用常规方法去解决往往运算比较繁杂，不妨运用向量作形与数的转化，则会大大简化过程。
二、例题解析
例1、椭圆的焦点为FF，点P为其上的动点，当∠FP F为钝角时，点P横坐标的取值范围是___。
解：F1（－,0）F2（,0）,设P（3cos,2sin）
为钝角
∴
=9cos2－5＋4sin2=5 cos2－1<0
解得： ∴点P横坐标的取值范围是（）
点评：解决与角有关的一类问题，总可以从数量积入手。本题中把条件中的角为钝角转化为向量的数量积为负值，通过坐标运算列出不等式，简洁明了。
例2、已知定点A(-1,0)和B(1,0)，P是圆(x-3)2+(y-4)2=4上的一动点，求的最大值和最小值。
分析：因为O为AB的中点，所以故可利用向量把问题转化为求向量的最值。
解：设已知圆的圆心为C，由已知可得：
又由中点公式得
所以
=
=
=
又因为 点P在圆(x-3)2+(y-4)2=4上,
所以 且
所以
即 故
所以的最大值为100，最小值为20。
点评：有些解几问题虽然没有直接用向量作为已知条件出现，但如果运用向量知识来解决，也会显得自然、简便，而且易入手。
例3、O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足，，则P的轨迹一定通过△ABC的（ ）
（A）外心 （B）内心 （C）重心 （D）垂心
分析：因为同向的单位向量，由向量加法的平行四边形则知是与∠ABC的角平分线（射线）同向的一个向量，又，知P点的轨迹是∠ABC的角平分线，从而点P的轨迹一定通过△ABC的内心。
反思：根据本题的结论，我们不难得到求一个角的平分线所在的直线方程的步骤；
由顶点坐标（含线段端点）或直线方程求得角两边的方向向量；
求出角平分线的方向向量
由点斜式或点向式得出角平分线方程。{直线的点向式方程：过P（），其方向向量为，其方程为}
例4、（2003年天津）已知常数，向量，经过原点以为方向向量的直线与经过定点以为方向向量的直线相交于点，其中．试问：是否存在两个定点，使得为定值，若存在，求出的坐标；若不存在，说明理由．
（本小题主要考查平面向量的概念和计算,求轨迹的方法，椭圆的方程和性质，利用方程判定曲线的性质，曲线与方程的关系等解析几何的基本思想和综合解题能力.）
解：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到两定点距离的和为定值.
∵， ∴=（λ，a），=（1，－2λa）.
因此，直线OP和AP的方程分别为 和 .
消去参数λ，得点的坐标满足方程.
整理得 ……① 因为所以得：
（i）当时，方程①是圆方程，故不存在合乎题意的定点E和F；
（ii）当时，方程①表示椭圆，焦点和为合乎题意的两个定点；
（iii）当时，方程①也表示椭圆，焦点和为合乎题意的两个定点.
点评：本题以平面向量为载体，考查求轨迹的方法、利用方程判定曲线的性质、曲线与方程的关系等解析几何的基本思想和综合解题能力。去掉平面向量的背景，我们不难看到，本题即为下题：
在△OAP中，O（0，0）、A（0，a）为两个定点，另两边OP与AP的斜率分别是，求P的轨迹。
例5．椭圆的中心是原点O，它的短轴长为，相应于焦点F（c，0）（）的准线与x轴相交于点A，|OF|=2|FA|，过点A的直线与椭圆相交于P、Q两点.
（1）求椭圆的方程及离心率；
（2）若，求直线PQ的方程；
（3）设（），过点P且平行于准线的直线与椭圆相交于另一点M，证明.
分析：本小题主要考查椭圆的标准方程和几何性质，直线方程，平面向量的计算，曲线和方程的关系等解析几何的基本思想方法和综合解题能力.
（1）解：由题意，可设椭圆的方程为.
由已知得解得
所以椭圆的方程为，离心率.
（2）解：由（1）可得A（3，0）.
设直线PQ的方程为.由方程组
得
依题意，得.
设，则， ① . ②
由直线PQ的方程得.于是
. ③
∵，∴. ④
由①②③④得，从而.
所以直线PQ的方程为或
（2）证明：.由已知得方程组
注意，解得
因，故
.
而，所以.
三、总结提炼
由于向量具有几何形式和代数形式的“双重身份”，使向量与解析几何之间有着密切联系，而新课程高考则突出了对向量与解析几何结合考查，这就要求我们在平时的解析几何教学与复习中，应抓住时机，有效地渗透向量有关知识，树立应用向量的意识。应充分挖掘课本素材，在教学中从推导有关公式、定理，例题讲解入手，让学生去品位、去领悟，在公式、定理的探索、形成中逐渐体会向量的工具性，逐渐形成应用向量的意识，在教学中还应注重引导学生善于运用一些问题的结论，加以引申，使之成为解题方法，体会向量解题的优越性，在教学中还应注重引导学生善于运用向量方法解题，逐步树立运用向量知识解题的意识。
向量与复数单元测试
1．设a是实数，且是实数，则
2.设点，,若点在直线上，且.则点的坐标为
3.已知向量，，且，则x为_____________
4.已知向量，若与垂直，则
5.若向量的夹角为，，则 .
6.复数等于
7. 向量，，若与平行，则等于
8.与向量，夹角相等的单位向量的坐标
9.如图，在中，是边上一点，则
.
10.设，已知两个向量，
，则向量长度的最大值是
11.如图，在中，点是的中点，过点的直线分别交直线，于不同的两点，若，，则的值为
12.虚数（x－2）+ yi其中x、y均为实数，当此虚数的模为1时，的取值范围是
13、 已知,⑴ 设.⑵ 如果求实数的值.
14、已知,,当为何值时，
（1）与垂直？ （2）与平行？平行时它们是同向还是反向？
15.已知之间有关系，其中k＞0,
（1）用k表示 ；②求的最小值，并求此时夹角的大小。
参考答案
1、1 2、或 3、4 4、2 5、2 6、 7、
8、 9、 10、 11、2
12、
13、解:⑴ ∵, ∴.
⑵
由已知得 .
14、解：
（1），
得
（2），得
此时，所以方向相反 ( http: / / wxc. / )
15、解：①:∵ ∴
即 ∴
∵，所以∴
②: ∵,∴
∴的最小值为
又∵ ∴
∴
C
A
B
M
N
P
（第13题）
A
第12题
C
D
B
A
B
C
D
P
C
y
x
A
o
B
11题
B
A
C
D
第9题