陕西省宝鸡市千阳高中2020-2021学年高一下学期5月月考数学试题 Word版含答案
文档属性
| 名称 | 陕西省宝鸡市千阳高中2020-2021学年高一下学期5月月考数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 281.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 19:11:26 | ||
图片预览


文档简介
千阳中学2020年高一数学5月月考题
(时间:120分钟 满分:120分)
一、选择题(12×5=60分)
1.为了调查全国人口的寿命,抽查了11个省(市)的2 500 名城镇居民,这2 500名城镇居民的寿命的全体是( )
A.总体 B.个体 C.样本 D.样本容量
2.下列抽样方法是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.可口可乐公司从仓库的1 000瓶可乐中一次性抽取20瓶进行质量检查
C.某连队从200名战士中,挑选出50名最优秀的战士参加抢险救灾
D.从10个手机中不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)
3.某单位有老年人28人,中年人36人,青年人81人,为了调查他们的身体状况,需从他们中抽取一个容量为16的样本,最适合抽取样本的方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.先从老年人中剔除一人,然后分层抽样
4.某工厂生产A、B、C三种不同型号的产品,产品的数量之比依次为3∶4∶7,现在用分层抽样的方法抽出容量为n的样本,样本中A型号产品有15件,那么样本容量n为( )
A.50 B.60 C.70 D.80
5.根据某市环境保护局公布2008~2013这六年的空气质量优良的天数,绘制成折线图如图,根据图中的信息可知,这六年的每年空气质量优良天数的中位数是( )
A.300 B.302.5 C.305 D.310
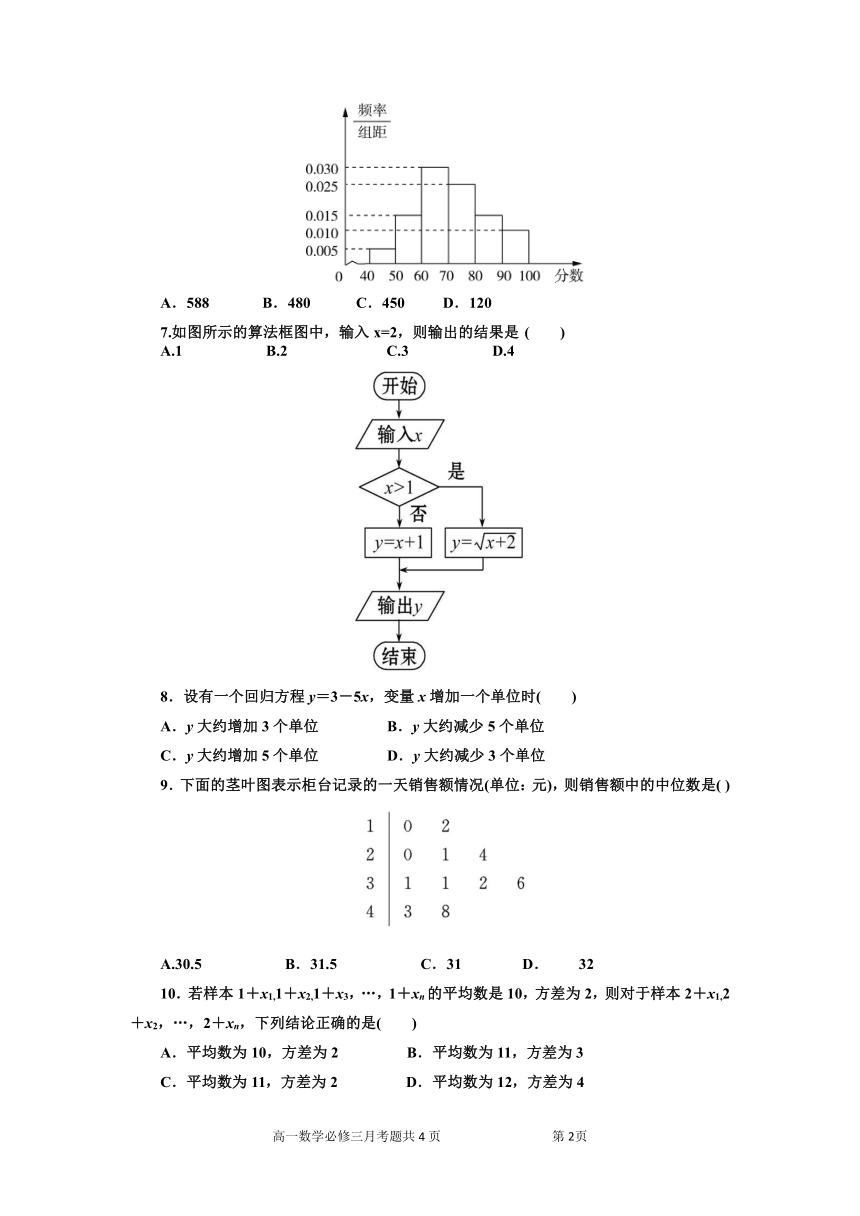
6.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
A.588 B.480 C.450 D.120
7.如图所示的算法框图中,输入x=2,则输出的结果是 ( )
A.1 B.2 C.3 D.4
8.设有一个回归方程y=3-5x,变量x增加一个单位时( )
A.y大约增加3个单位 B.y大约减少5个单位
C.y大约增加5个单位 D.y大约减少3个单位
9.下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是( )
A.30.5 B.31.5 C.31 D.32
10.若样本1+x1,1+x2,1+x3,…,1+xn的平均数是10,方差为2,则对于样本2+x1,2+x2,…,2+xn,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
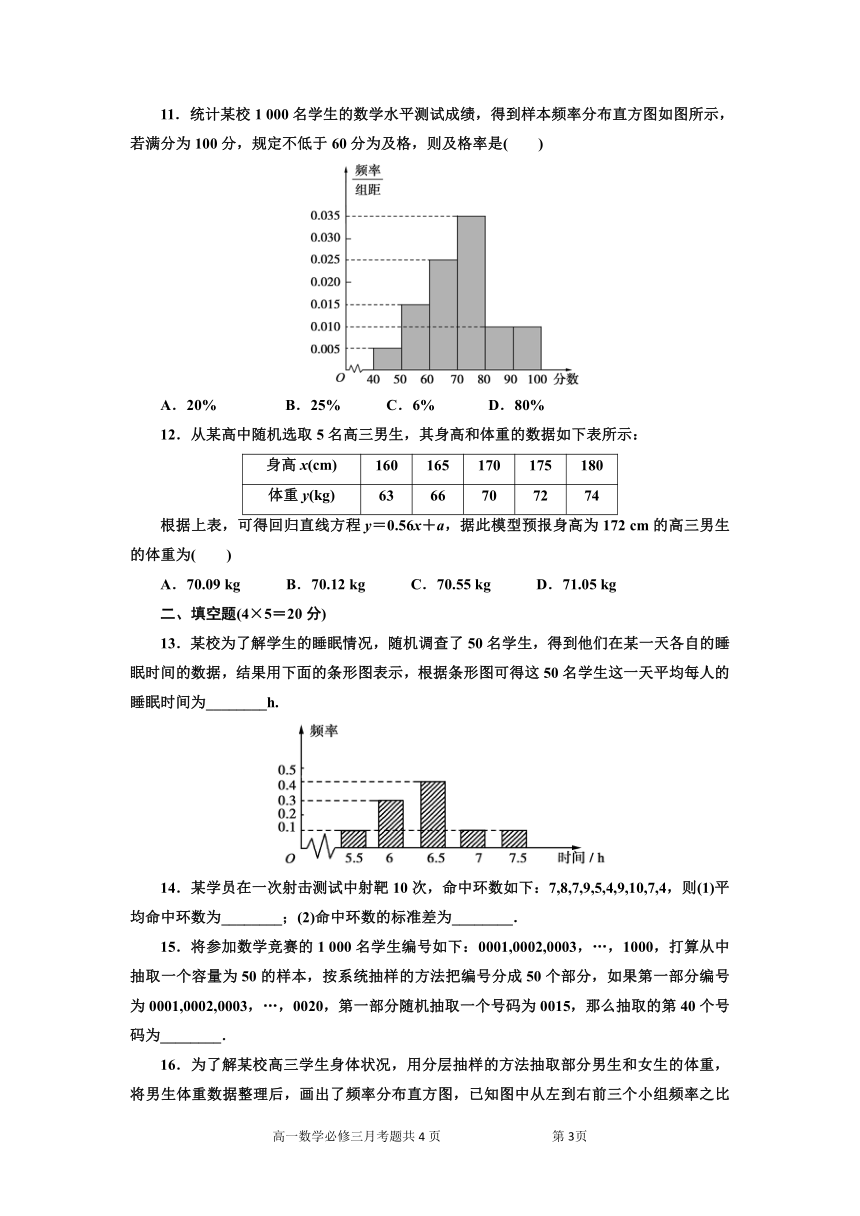
11.统计某校1 000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A.20% B.25% C.6% D.80%
12.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高x(cm)
160
165
170
175
180
体重y(kg)
63
66
70
72
74
根据上表,可得回归直线方程y=0.56x+a,据此模型预报身高为172 cm的高三男生的体重为( )
A.70.09 kg B.70.12 kg C.70.55 kg D.71.05 kg
二、填空题(4×5=20分)
13.某校为了解学生的睡眠情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用下面的条形图表示,根据条形图可得这50名学生这一天平均每人的睡眠时间为________h.
14.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,则(1)平均命中环数为________;(2)命中环数的标准差为________.
15.将参加数学竞赛的1 000名学生编号如下:0001,0002,0003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法把编号分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机抽取一个号码为0015,那么抽取的第40个号码为________.
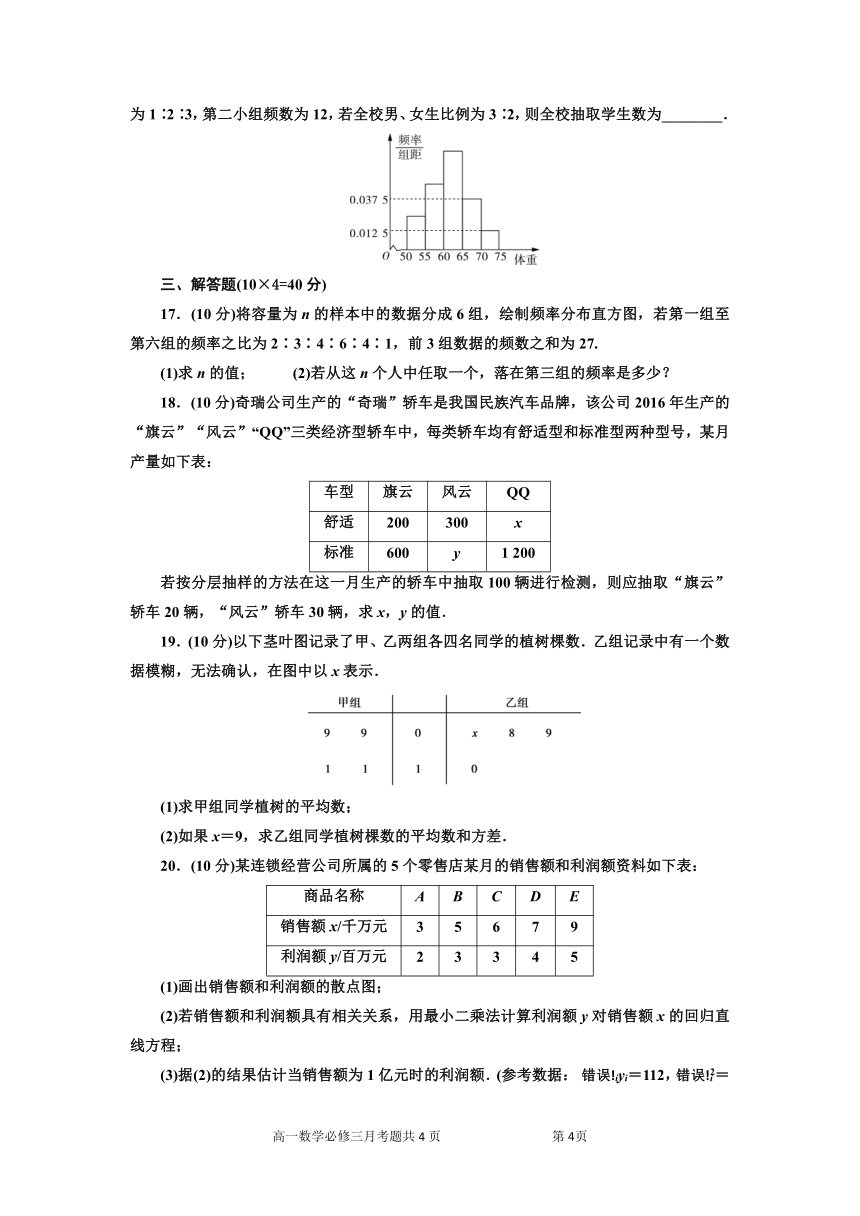
16.为了解某校高三学生身体状况,用分层抽样的方法抽取部分男生和女生的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
三、解答题(10×4=40分)
17.(10分)将容量为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1,前3组数据的频数之和为27.
(1)求n的值; (2)若从这n个人中任取一个,落在第三组的频率是多少?
18.(10分)奇瑞公司生产的“奇瑞”轿车是我国民族汽车品牌,该公司2016年生产的“旗云”“风云”“QQ”三类经济型轿车中,每类轿车均有舒适型和标准型两种型号,某月产量如下表:
车型
旗云
风云
QQ
舒适
200
300
x
标准
600
y
1 200
若按分层抽样的方法在这一月生产的轿车中抽取100辆进行检测,则应抽取“旗云”轿车20辆,“风云”轿车30辆,求x,y的值.
19.(10分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以x表示.
(1)求甲组同学植树的平均数;
(2)如果x=9,求乙组同学植树棵数的平均数和方差.
20.(10分)某连锁经营公司所属的5个零售店某月的销售额和利润额资料如下表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)据(2)的结果估计当销售额为1亿元时的利润额.(参考数据: iyi=112,=200)
千阳中学2020年高一数学考题答案版
(时间:120分钟 满分:120分)
一、选择题(12×5=60分)
1.为了调查全国人口的寿命,抽查了11个省(市)的2 500 名城镇居民,这2 500名城镇居民的寿命的全体是( )
A.总体 B.个体 C.样本 D.样本容量
解析:选C
2.下列抽样方法是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.可口可乐公司从仓库的1 000瓶可乐中一次性抽取20瓶进行质量检查
C.某连队从200名战士中,挑选出50名最优秀的战士参加抢险救灾
D.从10个手机中不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)
解析:选D A中平面直角坐标系中有无数个点,不是简单随机抽样;B中是一次性抽取20瓶,不符合逐个抽取的特点,故不是简单随机抽样;C中50名战士是最优秀的,不是等可能抽取,所以不是简单随机抽样;D是简单随机抽样.
3.某单位有老年人28人,中年人36人,青年人81人,为了调查他们的身体状况,需从他们中抽取一个容量为16的样本,最适合抽取样本的方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.先从老年人中剔除一人,然后分层抽样
解析:选D ∵老年人、中年人、青年人的身体状况有明显的差异,∴应选用分层抽样.∵分层抽样是按比例抽取,∴分的层应成比例27∶36∶81=3∶4∶9,∴先从老年人中剔除一人后,再用分层抽样抽取样本.
4.某工厂生产A、B、C三种不同型号的产品,产品的数量之比依次为3∶4∶7,现在用分层抽样的方法抽出容量为n的样本,样本中A型号产品有15件,那么样本容量n为()
A.50 B.60 C.70 D.80
解析:选C 由题意得==,得n==70.
5.根据某市环境保护局公布2008~2013这六年的空气质量优良的天数,绘制成折线图如图,根据图中的信息可知,这六年的每年空气质量优良天数的中位数是( )
A.300 B.302.5 C.305 D.310
解析:选B 该组数据为290,295,300,305,305,315,共6个数,中位数为=302.5.
6.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
A.588 B.480 C.450 D.120
解析:选B 根据频率分布直方图,成绩不低于60分的频率为1-10×(0.005+0.015)=0.8.由于该校高一年级共有学生600人,利用样本估计总体的思想,可估计该校高一年级模块测试成绩不低于60分的人数为600×0.8=480(人).
7.如图所示的算法框图中,输入x=2,则输出的结果是 ( B )
A.1 B.2 C.3 D.4
8.设有一个回归方程y=3-5x,变量x增加一个单位时( )
A.y大约增加3个单位 B.y大约减少5个单位
C.y大约增加5个单位 D.y大约减少3个单位
解析:选B 令f(x)=3-5x,则f(x+1)-f(x)=-5(x+1)-(-5x)=-5x-5+5x=-5,则变量x增加一个单位,y大约减少5个单位.
9.下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是( )
A.30.5 B.31.5 C.31 D.32
解析:选C 销售额数据为:10,12,20,21,24,31,31,32,36,43,48,共11个数,中位数为31.
10.若样本1+x1,1+x2,1+x3,…,1+xn的平均数是10,方差为2,则对于样本2+x1,2+x2,…,2+xn,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
解析:选C 由平均数及方差的计算公式知,新数据的平均数为10+1=11,方差不变,还是2.
11.统计某校1 000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A.20% B.25% C.6% D.80%
解析:选D 及格的频率为(0.025+0.035+0.010×2)×10=0.8,∴及格率为80%.
12.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高x(cm)
160
165
170
175
180
体重y(kg)
63
66
70
72
74
根据上表,可得回归直线方程y=0.56x+a,据此模型预报身高为172 cm的高三男生的体重为( )
A.70.09 kg B.70.12 kg C.70.55 kg D.71.05 kg
解析:选B ==170,
==69.
又y=0.56x+a过点(,),∴69=0.56×170+a,∴a=-26.2.
∴回归直线方程为y=0.56x-26.2,当x=172时,y=70.12.
二、填空题(4×5=20分)
13.某校为了解学生的睡眠情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用下面的条形图表示,根据条形图可得这50名学生这一天平均每人的睡眠时间为________h.
解析:=0.1×(5.5+7+7.5)+0.3×6+0.4×6.5=6.4.答案:6.4
14.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,则(1)平均命中环数为________;(2)命中环数的标准差为________.
解析:由=7,
s2=
==4.∴s==2.答案:(1)7 (2)2
15.将参加数学竞赛的1 000名学生编号如下:0001,0002,0003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法把编号分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机抽取一个号码为0015,那么抽取的第40个号码为________.
解析:第40个号码为0015+39×20=0795.答案:0795
16.为了解某校高三学生身体状况,用分层抽样的方法抽取部分男生和女生的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
解析:∵第四小组和第五小组的频率之和为(0.037 5+0.012 5)×5=0.25,∴前三组的频率之和为1-0.25=0.75.∴第二小组的频率为0.75×=0.25.又第二小组的频数为12,∴抽取的男生人数为12÷0.25=48.∴抽取的女生人数为48×=32,∴全校共抽取48+32=80(人).答案:80
三、解答题(10×4=40分)
17.(10分)将容量为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1,前3组数据的频数之和为27.
(1)求n的值;(2)若从这n个人中任取一个,落在第三组的频率是多少?
解:(1)设第一组至第六组的样本数据的频数分别为2x,3x,4x,6x,4x,x,则2x+3x+4x=27,∴x=3,∴n=20x=60.
(2)由(1)知第三组人数为4x=12,∴落在第三组的频率为=.
18.(10分)奇瑞公司生产的“奇瑞”轿车是我国民族汽车品牌,该公司2016年生产的“旗云”“风云”“QQ”三类经济型轿车中,每类轿车均有舒适型和标准型两种型号,某月产量如下表:
车型
旗云
风云
QQ
舒适
200
300
x
标准
600
y
1 200
若按分层抽样的方法在这一月生产的轿车中抽取100辆进行检测,则应抽取“旗云”轿车20辆,“风云”轿车30辆,求x,y的值.
解:由题意得==,即解得∴x的值为800,y的值为900.
19.(10分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以x表示.
(1)求甲组同学植树的平均数;
(2)如果x=9,求乙组同学植树棵数的平均数和方差.
解:(1)由=10知甲组同学植树的平均数为10.
(2)当x=9时,乙组同学植树棵数的平均数为=9,
∴方差s2==.
20.(10分)某连锁经营公司所属的5个零售店某月的销售额和利润额资料如下表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)据(2)的结果估计当销售额为1亿元时的利润额.
解:(1)销售额和利润额的散点图如图.
(2)销售额和利润额具有相关关系,列表如下:
xi
3
5
6
7
9
yi
2
3
3
4
5
xiyi
6
15
18
28
45
=6,=3.4,iyi=112,=200
所以b==0.5,
a=-b =3.4-0.5×6=0.4.
从而得回归直线方程为y=0.5x+0.4.
(3)当x=10时,y=0.5×10+0.4=5.4(百万元).故当销售额为1亿元时,利润额估计为540万元.
(时间:120分钟 满分:120分)
一、选择题(12×5=60分)
1.为了调查全国人口的寿命,抽查了11个省(市)的2 500 名城镇居民,这2 500名城镇居民的寿命的全体是( )
A.总体 B.个体 C.样本 D.样本容量
2.下列抽样方法是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.可口可乐公司从仓库的1 000瓶可乐中一次性抽取20瓶进行质量检查
C.某连队从200名战士中,挑选出50名最优秀的战士参加抢险救灾
D.从10个手机中不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)
3.某单位有老年人28人,中年人36人,青年人81人,为了调查他们的身体状况,需从他们中抽取一个容量为16的样本,最适合抽取样本的方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.先从老年人中剔除一人,然后分层抽样
4.某工厂生产A、B、C三种不同型号的产品,产品的数量之比依次为3∶4∶7,现在用分层抽样的方法抽出容量为n的样本,样本中A型号产品有15件,那么样本容量n为( )
A.50 B.60 C.70 D.80
5.根据某市环境保护局公布2008~2013这六年的空气质量优良的天数,绘制成折线图如图,根据图中的信息可知,这六年的每年空气质量优良天数的中位数是( )
A.300 B.302.5 C.305 D.310
6.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
A.588 B.480 C.450 D.120
7.如图所示的算法框图中,输入x=2,则输出的结果是 ( )
A.1 B.2 C.3 D.4
8.设有一个回归方程y=3-5x,变量x增加一个单位时( )
A.y大约增加3个单位 B.y大约减少5个单位
C.y大约增加5个单位 D.y大约减少3个单位
9.下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是( )
A.30.5 B.31.5 C.31 D.32
10.若样本1+x1,1+x2,1+x3,…,1+xn的平均数是10,方差为2,则对于样本2+x1,2+x2,…,2+xn,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
11.统计某校1 000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A.20% B.25% C.6% D.80%
12.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高x(cm)
160
165
170
175
180
体重y(kg)
63
66
70
72
74
根据上表,可得回归直线方程y=0.56x+a,据此模型预报身高为172 cm的高三男生的体重为( )
A.70.09 kg B.70.12 kg C.70.55 kg D.71.05 kg
二、填空题(4×5=20分)
13.某校为了解学生的睡眠情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用下面的条形图表示,根据条形图可得这50名学生这一天平均每人的睡眠时间为________h.
14.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,则(1)平均命中环数为________;(2)命中环数的标准差为________.
15.将参加数学竞赛的1 000名学生编号如下:0001,0002,0003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法把编号分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机抽取一个号码为0015,那么抽取的第40个号码为________.
16.为了解某校高三学生身体状况,用分层抽样的方法抽取部分男生和女生的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
三、解答题(10×4=40分)
17.(10分)将容量为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1,前3组数据的频数之和为27.
(1)求n的值; (2)若从这n个人中任取一个,落在第三组的频率是多少?
18.(10分)奇瑞公司生产的“奇瑞”轿车是我国民族汽车品牌,该公司2016年生产的“旗云”“风云”“QQ”三类经济型轿车中,每类轿车均有舒适型和标准型两种型号,某月产量如下表:
车型
旗云
风云
舒适
200
300
x
标准
600
y
1 200
若按分层抽样的方法在这一月生产的轿车中抽取100辆进行检测,则应抽取“旗云”轿车20辆,“风云”轿车30辆,求x,y的值.
19.(10分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以x表示.
(1)求甲组同学植树的平均数;
(2)如果x=9,求乙组同学植树棵数的平均数和方差.
20.(10分)某连锁经营公司所属的5个零售店某月的销售额和利润额资料如下表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)据(2)的结果估计当销售额为1亿元时的利润额.(参考数据: iyi=112,=200)
千阳中学2020年高一数学考题答案版
(时间:120分钟 满分:120分)
一、选择题(12×5=60分)
1.为了调查全国人口的寿命,抽查了11个省(市)的2 500 名城镇居民,这2 500名城镇居民的寿命的全体是( )
A.总体 B.个体 C.样本 D.样本容量
解析:选C
2.下列抽样方法是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.可口可乐公司从仓库的1 000瓶可乐中一次性抽取20瓶进行质量检查
C.某连队从200名战士中,挑选出50名最优秀的战士参加抢险救灾
D.从10个手机中不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)
解析:选D A中平面直角坐标系中有无数个点,不是简单随机抽样;B中是一次性抽取20瓶,不符合逐个抽取的特点,故不是简单随机抽样;C中50名战士是最优秀的,不是等可能抽取,所以不是简单随机抽样;D是简单随机抽样.
3.某单位有老年人28人,中年人36人,青年人81人,为了调查他们的身体状况,需从他们中抽取一个容量为16的样本,最适合抽取样本的方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.先从老年人中剔除一人,然后分层抽样
解析:选D ∵老年人、中年人、青年人的身体状况有明显的差异,∴应选用分层抽样.∵分层抽样是按比例抽取,∴分的层应成比例27∶36∶81=3∶4∶9,∴先从老年人中剔除一人后,再用分层抽样抽取样本.
4.某工厂生产A、B、C三种不同型号的产品,产品的数量之比依次为3∶4∶7,现在用分层抽样的方法抽出容量为n的样本,样本中A型号产品有15件,那么样本容量n为()
A.50 B.60 C.70 D.80
解析:选C 由题意得==,得n==70.
5.根据某市环境保护局公布2008~2013这六年的空气质量优良的天数,绘制成折线图如图,根据图中的信息可知,这六年的每年空气质量优良天数的中位数是( )
A.300 B.302.5 C.305 D.310
解析:选B 该组数据为290,295,300,305,305,315,共6个数,中位数为=302.5.
6.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
A.588 B.480 C.450 D.120
解析:选B 根据频率分布直方图,成绩不低于60分的频率为1-10×(0.005+0.015)=0.8.由于该校高一年级共有学生600人,利用样本估计总体的思想,可估计该校高一年级模块测试成绩不低于60分的人数为600×0.8=480(人).
7.如图所示的算法框图中,输入x=2,则输出的结果是 ( B )
A.1 B.2 C.3 D.4
8.设有一个回归方程y=3-5x,变量x增加一个单位时( )
A.y大约增加3个单位 B.y大约减少5个单位
C.y大约增加5个单位 D.y大约减少3个单位
解析:选B 令f(x)=3-5x,则f(x+1)-f(x)=-5(x+1)-(-5x)=-5x-5+5x=-5,则变量x增加一个单位,y大约减少5个单位.
9.下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是( )
A.30.5 B.31.5 C.31 D.32
解析:选C 销售额数据为:10,12,20,21,24,31,31,32,36,43,48,共11个数,中位数为31.
10.若样本1+x1,1+x2,1+x3,…,1+xn的平均数是10,方差为2,则对于样本2+x1,2+x2,…,2+xn,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
解析:选C 由平均数及方差的计算公式知,新数据的平均数为10+1=11,方差不变,还是2.
11.统计某校1 000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A.20% B.25% C.6% D.80%
解析:选D 及格的频率为(0.025+0.035+0.010×2)×10=0.8,∴及格率为80%.
12.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高x(cm)
160
165
170
175
180
体重y(kg)
63
66
70
72
74
根据上表,可得回归直线方程y=0.56x+a,据此模型预报身高为172 cm的高三男生的体重为( )
A.70.09 kg B.70.12 kg C.70.55 kg D.71.05 kg
解析:选B ==170,
==69.
又y=0.56x+a过点(,),∴69=0.56×170+a,∴a=-26.2.
∴回归直线方程为y=0.56x-26.2,当x=172时,y=70.12.
二、填空题(4×5=20分)
13.某校为了解学生的睡眠情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用下面的条形图表示,根据条形图可得这50名学生这一天平均每人的睡眠时间为________h.
解析:=0.1×(5.5+7+7.5)+0.3×6+0.4×6.5=6.4.答案:6.4
14.某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,则(1)平均命中环数为________;(2)命中环数的标准差为________.
解析:由=7,
s2=
==4.∴s==2.答案:(1)7 (2)2
15.将参加数学竞赛的1 000名学生编号如下:0001,0002,0003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法把编号分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机抽取一个号码为0015,那么抽取的第40个号码为________.
解析:第40个号码为0015+39×20=0795.答案:0795
16.为了解某校高三学生身体状况,用分层抽样的方法抽取部分男生和女生的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
解析:∵第四小组和第五小组的频率之和为(0.037 5+0.012 5)×5=0.25,∴前三组的频率之和为1-0.25=0.75.∴第二小组的频率为0.75×=0.25.又第二小组的频数为12,∴抽取的男生人数为12÷0.25=48.∴抽取的女生人数为48×=32,∴全校共抽取48+32=80(人).答案:80
三、解答题(10×4=40分)
17.(10分)将容量为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1,前3组数据的频数之和为27.
(1)求n的值;(2)若从这n个人中任取一个,落在第三组的频率是多少?
解:(1)设第一组至第六组的样本数据的频数分别为2x,3x,4x,6x,4x,x,则2x+3x+4x=27,∴x=3,∴n=20x=60.
(2)由(1)知第三组人数为4x=12,∴落在第三组的频率为=.
18.(10分)奇瑞公司生产的“奇瑞”轿车是我国民族汽车品牌,该公司2016年生产的“旗云”“风云”“QQ”三类经济型轿车中,每类轿车均有舒适型和标准型两种型号,某月产量如下表:
车型
旗云
风云
舒适
200
300
x
标准
600
y
1 200
若按分层抽样的方法在这一月生产的轿车中抽取100辆进行检测,则应抽取“旗云”轿车20辆,“风云”轿车30辆,求x,y的值.
解:由题意得==,即解得∴x的值为800,y的值为900.
19.(10分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以x表示.
(1)求甲组同学植树的平均数;
(2)如果x=9,求乙组同学植树棵数的平均数和方差.
解:(1)由=10知甲组同学植树的平均数为10.
(2)当x=9时,乙组同学植树棵数的平均数为=9,
∴方差s2==.
20.(10分)某连锁经营公司所属的5个零售店某月的销售额和利润额资料如下表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)据(2)的结果估计当销售额为1亿元时的利润额.
解:(1)销售额和利润额的散点图如图.
(2)销售额和利润额具有相关关系,列表如下:
xi
3
5
6
7
9
yi
2
3
3
4
5
xiyi
6
15
18
28
45
=6,=3.4,iyi=112,=200
所以b==0.5,
a=-b =3.4-0.5×6=0.4.
从而得回归直线方程为y=0.5x+0.4.
(3)当x=10时,y=0.5×10+0.4=5.4(百万元).故当销售额为1亿元时,利润额估计为540万元.
同课章节目录
