8.1 基本立体图形(2)课件(共19张PPT)
文档属性
| 名称 | 8.1 基本立体图形(2)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 14:27:52 | ||
图片预览


文档简介
第8章 立体几何初步
8.1 基本立体图形(2)
高中数学人教A版(2019)必修 第二册
圆柱
以矩形的一边所在的直线为旋转轴,其余三边旋转一周形成的面围城的旋转体叫做圆柱.
旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论转到什么位置,平行于轴的边都叫做圆柱侧面的母线.
圆柱的定义
探究新知
圆柱
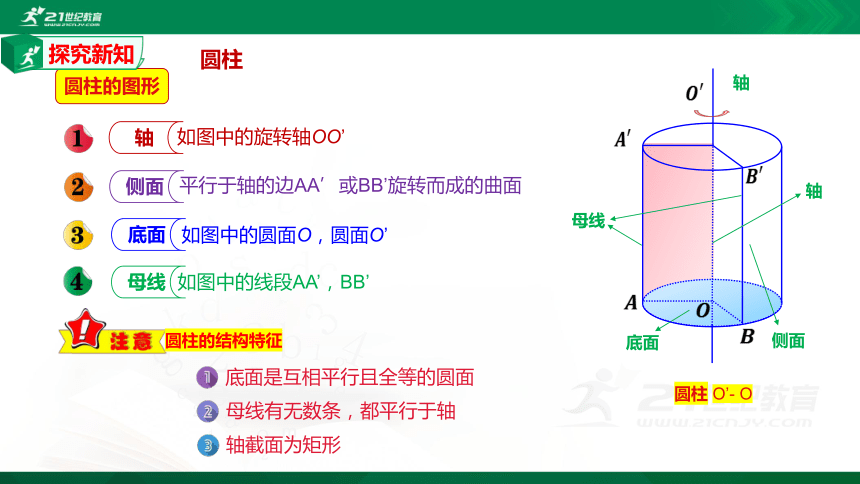
圆柱的图形
如图中的旋转轴OO’
轴
侧面
平行于轴的边AA’或BB’旋转而成的曲面
底面
如图中的圆面O,圆面O’
母线
如图中的线段AA’,BB’
圆柱的结构特征
底面是互相平行且全等的圆面
母线有无数条,都平行于轴
轴截面为矩形
????′
?
????′
?
????′
?
????
?
????
?
????
?
母线
轴
侧面
底面
圆柱 O’- O
轴
探究新知
圆柱
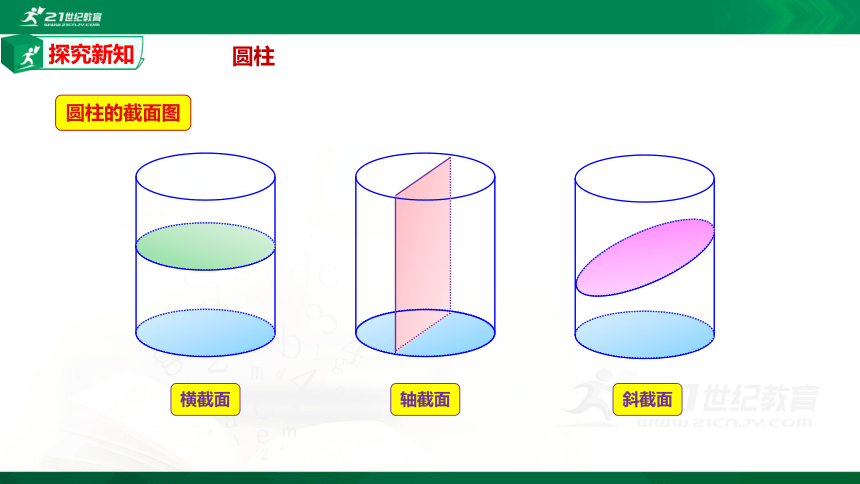
圆柱的截面图
横截面
轴截面
斜截面
探究新知
圆锥
圆锥的定义
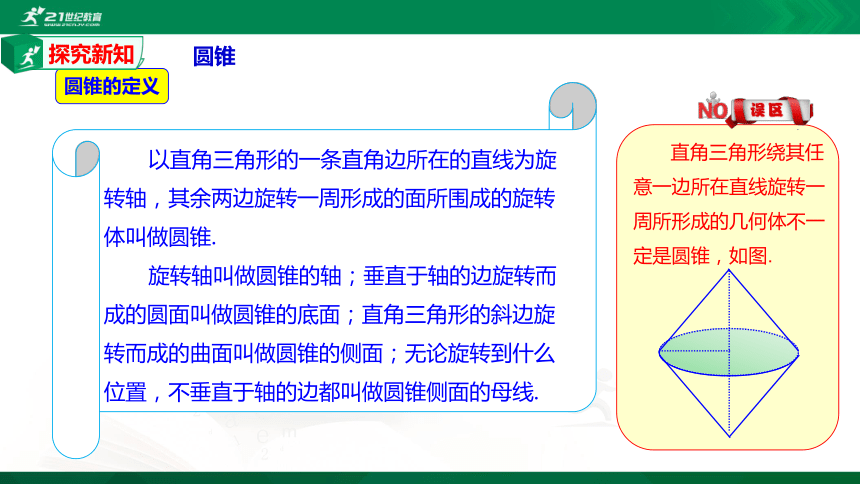
以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.
旋转轴叫做圆锥的轴;垂直于轴的边旋转而成的圆面叫做圆锥的底面;直角三角形的斜边旋转而成的曲面叫做圆锥的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆锥侧面的母线.
直角三角形绕其任意一边所在直线旋转一周所形成的几何体不一定是圆锥,如图.
探究新知
圆锥
2
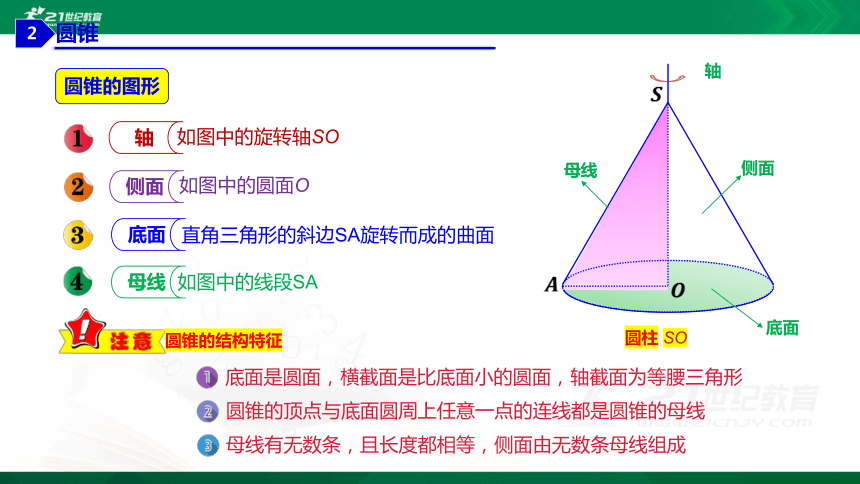
圆锥的图形
如图中的旋转轴SO
轴
侧面
底面
直角三角形的斜边SA旋转而成的曲面
母线
如图中的线段SA
圆锥的结构特征
????
?
????
?
????
?
侧面
母线
底面
轴
如图中的圆面O
底面是圆面,横截面是比底面小的圆面,轴截面为等腰三角形
圆锥的顶点与底面圆周上任意一点的连线都是圆锥的母线
母线有无数条,且长度都相等,侧面由无数条母线组成
圆柱 SO
圆锥
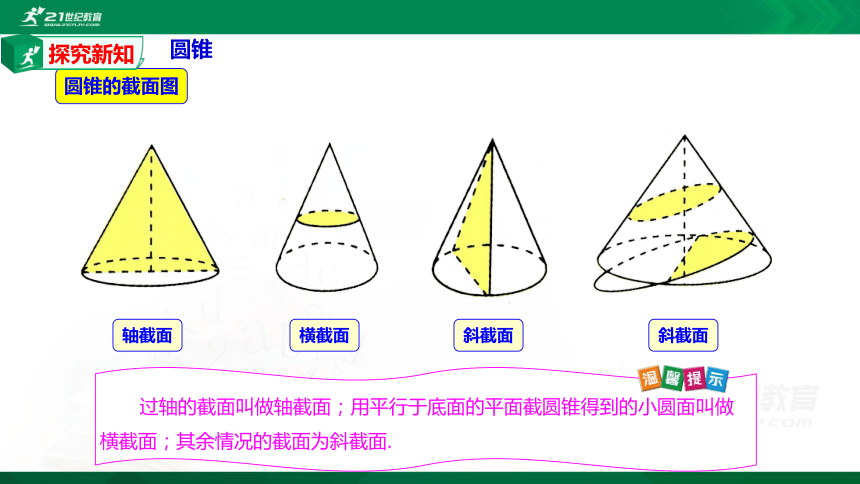
圆锥的截面图
轴截面
过轴的截面叫做轴截面;用平行于底面的平面截圆锥得到的小圆面叫做横截面;其余情况的截面为斜截面.
横截面
斜截面
斜截面
探究新知
圆台
圆台的定义
用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.
原圆锥的底面和截面分别叫做圆台的下底面和上底面.
圆台可以看做以直角梯形垂直于底面的腰所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体.
与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线.
探究新知
圆台
圆台的定义
如图中的旋转轴O’O
轴
侧面
底面
直角梯形的非直角腰AA’旋转而成的曲面
母线
如图中的线段AA’,BB’
圆台的结构特征
????
?
????
?
上底面
轴
下底面
如图中的圆面O
上、下底面是半径不相等且互相平行的圆面
母线有无数条,且长度相等,各条母线的延长线交于一点
轴截面为等腰梯形
圆台 O’O
????
?
????′
?
????′
?
????′
?
侧面
母线
探究新知
圆台
柱、锥、台之间的内在联系及其相互转化的条件
棱柱
棱台
棱锥
上下底面全等
上底退缩为点
底面转化
为等圆
底面转化
为不等圆
底面转
化为圆
圆柱
圆台
圆锥
上下底面全等
上底退缩为点
探究新知
球
4
棱台的定义
半圆以它的直径所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球.
半圆的圆心叫做球的球心;连接球心和球面上任意一点的线段叫做球的半径;连接球面上两点并且经过球心的线段叫做球的直径.
球
球的图形
如图中的旋转轴O’O
轴
球心
半径
如图中的OA、OB、OC
球面
即球的表面,半圆旋转一周而成的曲面
圆台的结构特征
如图中的点O
球是旋转体,由球面及所围成的空间部分构成
用一个平面去截球,截面都是圆面,过球心为大圆,不过球心为小圆
????
?
????
?
????
?
????
?
????′
?
轴
半径
球体
包括球面和球面所围成的空间部分
球 O
探究新知
简单组合体
简单组合体的定义
现实世界中的物体表示的是几何体,除了柱体、椎体、台体和球等简单几何体外,还有大量的几何体是由简单几何体组合而成的,这些几何体称作简单几何体.
简单组合体的构成形式
——简单几何体拼接、截去或挖去一部分
探究新知
柱、锥、台的展开图与侧面图
探究新知
柱、锥、台的展开图与侧面图
探究新知
由平面图形构成旋转体的误区
如图所示,四边形ABCD为直角梯形,试着作出绕其各
条边所在直线旋转所得到的几何体.
【解析】四边形ABCD有四条边,分四种情况考虑:
(1)以AD所在直线为旋转轴,形成的几何体是圆台,如图①所示;
(2)以AB所在直线为旋转轴,形成的几何体是一个圆锥和一个圆柱的组合体,如图②;
(3)以CD所在直线为旋转轴,形成的几何体是圆柱中挖去一个圆锥的组合体,如图③;
????
?
????
?
????
?
????
?
(4)以BC所在直线为旋转轴,形成的几何体是圆台上边内部挖去一个倒立的小圆锥,
下面叠加一个倒立的大圆锥,如图④
①
②
③
④
已知一个棱长为6cm的正方体塑料盒子(无上盖),上口放着一个半径为5cm的钢球(钢球有一部分在盒子里面),求球心到盒底的距离.
题①
——简单组合体中的简单运算
【解析】如图所示,球心到盒底的距离可以看做是一个组合体的上顶点到下底
面的距离,这个组合体可以看做下面是棱长为6cm的正方体,上面是
以球心为顶点,正方体上底面截钢球所得的圆面为底面的圆
锥.圆锥的底面半径为3cm,母线长为5cm,则圆锥的高就是
52?32=4(????????)
?
所以球心到盒底的距离为 6+4=10cm.
谢谢聆听
8.1 基本立体图形(2)
高中数学人教A版(2019)必修 第二册
圆柱
以矩形的一边所在的直线为旋转轴,其余三边旋转一周形成的面围城的旋转体叫做圆柱.
旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论转到什么位置,平行于轴的边都叫做圆柱侧面的母线.
圆柱的定义
探究新知
圆柱
圆柱的图形
如图中的旋转轴OO’
轴
侧面
平行于轴的边AA’或BB’旋转而成的曲面
底面
如图中的圆面O,圆面O’
母线
如图中的线段AA’,BB’
圆柱的结构特征
底面是互相平行且全等的圆面
母线有无数条,都平行于轴
轴截面为矩形
????′
?
????′
?
????′
?
????
?
????
?
????
?
母线
轴
侧面
底面
圆柱 O’- O
轴
探究新知
圆柱
圆柱的截面图
横截面
轴截面
斜截面
探究新知
圆锥
圆锥的定义
以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.
旋转轴叫做圆锥的轴;垂直于轴的边旋转而成的圆面叫做圆锥的底面;直角三角形的斜边旋转而成的曲面叫做圆锥的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆锥侧面的母线.
直角三角形绕其任意一边所在直线旋转一周所形成的几何体不一定是圆锥,如图.
探究新知
圆锥
2
圆锥的图形
如图中的旋转轴SO
轴
侧面
底面
直角三角形的斜边SA旋转而成的曲面
母线
如图中的线段SA
圆锥的结构特征
????
?
????
?
????
?
侧面
母线
底面
轴
如图中的圆面O
底面是圆面,横截面是比底面小的圆面,轴截面为等腰三角形
圆锥的顶点与底面圆周上任意一点的连线都是圆锥的母线
母线有无数条,且长度都相等,侧面由无数条母线组成
圆柱 SO
圆锥
圆锥的截面图
轴截面
过轴的截面叫做轴截面;用平行于底面的平面截圆锥得到的小圆面叫做横截面;其余情况的截面为斜截面.
横截面
斜截面
斜截面
探究新知
圆台
圆台的定义
用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.
原圆锥的底面和截面分别叫做圆台的下底面和上底面.
圆台可以看做以直角梯形垂直于底面的腰所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体.
与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线.
探究新知
圆台
圆台的定义
如图中的旋转轴O’O
轴
侧面
底面
直角梯形的非直角腰AA’旋转而成的曲面
母线
如图中的线段AA’,BB’
圆台的结构特征
????
?
????
?
上底面
轴
下底面
如图中的圆面O
上、下底面是半径不相等且互相平行的圆面
母线有无数条,且长度相等,各条母线的延长线交于一点
轴截面为等腰梯形
圆台 O’O
????
?
????′
?
????′
?
????′
?
侧面
母线
探究新知
圆台
柱、锥、台之间的内在联系及其相互转化的条件
棱柱
棱台
棱锥
上下底面全等
上底退缩为点
底面转化
为等圆
底面转化
为不等圆
底面转
化为圆
圆柱
圆台
圆锥
上下底面全等
上底退缩为点
探究新知
球
4
棱台的定义
半圆以它的直径所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球.
半圆的圆心叫做球的球心;连接球心和球面上任意一点的线段叫做球的半径;连接球面上两点并且经过球心的线段叫做球的直径.
球
球的图形
如图中的旋转轴O’O
轴
球心
半径
如图中的OA、OB、OC
球面
即球的表面,半圆旋转一周而成的曲面
圆台的结构特征
如图中的点O
球是旋转体,由球面及所围成的空间部分构成
用一个平面去截球,截面都是圆面,过球心为大圆,不过球心为小圆
????
?
????
?
????
?
????
?
????′
?
轴
半径
球体
包括球面和球面所围成的空间部分
球 O
探究新知
简单组合体
简单组合体的定义
现实世界中的物体表示的是几何体,除了柱体、椎体、台体和球等简单几何体外,还有大量的几何体是由简单几何体组合而成的,这些几何体称作简单几何体.
简单组合体的构成形式
——简单几何体拼接、截去或挖去一部分
探究新知
柱、锥、台的展开图与侧面图
探究新知
柱、锥、台的展开图与侧面图
探究新知
由平面图形构成旋转体的误区
如图所示,四边形ABCD为直角梯形,试着作出绕其各
条边所在直线旋转所得到的几何体.
【解析】四边形ABCD有四条边,分四种情况考虑:
(1)以AD所在直线为旋转轴,形成的几何体是圆台,如图①所示;
(2)以AB所在直线为旋转轴,形成的几何体是一个圆锥和一个圆柱的组合体,如图②;
(3)以CD所在直线为旋转轴,形成的几何体是圆柱中挖去一个圆锥的组合体,如图③;
????
?
????
?
????
?
????
?
(4)以BC所在直线为旋转轴,形成的几何体是圆台上边内部挖去一个倒立的小圆锥,
下面叠加一个倒立的大圆锥,如图④
①
②
③
④
已知一个棱长为6cm的正方体塑料盒子(无上盖),上口放着一个半径为5cm的钢球(钢球有一部分在盒子里面),求球心到盒底的距离.
题①
——简单组合体中的简单运算
【解析】如图所示,球心到盒底的距离可以看做是一个组合体的上顶点到下底
面的距离,这个组合体可以看做下面是棱长为6cm的正方体,上面是
以球心为顶点,正方体上底面截钢球所得的圆面为底面的圆
锥.圆锥的底面半径为3cm,母线长为5cm,则圆锥的高就是
52?32=4(????????)
?
所以球心到盒底的距离为 6+4=10cm.
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
