7.2.2 复数的乘除运算课件(共18张PPT)
文档属性
| 名称 | 7.2.2 复数的乘除运算课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览






文档简介
第7章 复数
7.2.2 复数的乘除运算
????????????????=????????????????
?
(????????????????)????????=????????(????????????????)
?
????????????????+????????=????????????????+????????????????
?
高中数学人教A版(2019)必修 第二册
复数代数形式的乘法运算
复数的乘法法则
设 ????????=a+b?,????2=????+?????(????,????,????,????∈????) 是任意两个复数,那么它们的积
?
a+b?????+????????=????????+?????????????+?????????????+?????????????2=?????????????????+????????+????????????
?
两个复数的积仍然是一个确定的复数
在复数中,完全平方公式,平方差公
式仍然适用
可以看出,两个复数相乘,类似于两个多项式相乘,只要在所得的结果中把 ????2 换成-1,并且把实部与虚部分别合并即可.
?
探究新知
复数代数形式的乘法运算
复数乘法满足的交换律
复数的乘法满足交换律、结合律,以及对加法的分配律,则对任意的 ????1,????2,????3∈?????,有如下规律成立:
?
【计算】(7?????)(4?3????)
?
????????????????=????????????????
?
(????????????????)????????=????????(????????????????)
?
????????????????+????????=????????????????+????????????????
?
【解】(7?????)(4?3????)
?
=28?21?????4????+3????2
?
=28?25?????3
?
=25?25????
?
例题讲解
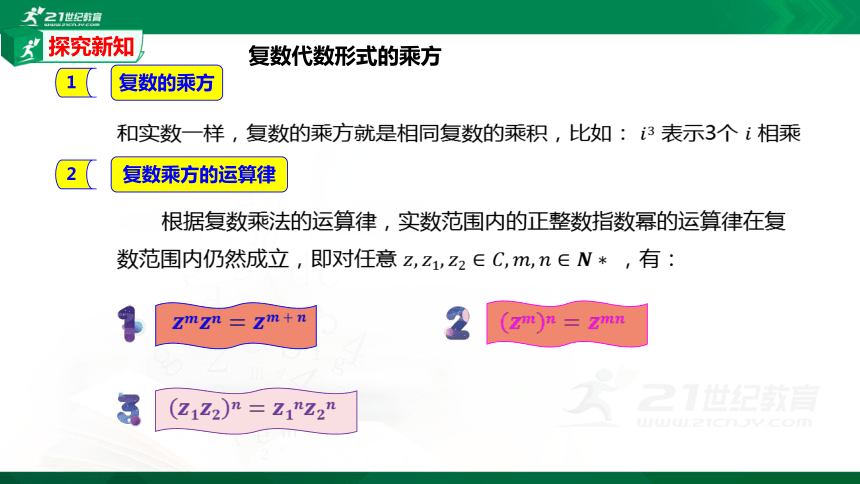
复数代数形式的乘方
复数的乘方
和实数一样,复数的乘方就是相同复数的乘积,比如: ????3 表示3个 ???? 相乘
?
1
复数乘方的运算律
2
根据复数乘法的运算律,实数范围内的正整数指数幂的运算律在复数范围内仍然成立,即对任意 ????,????1,????2∈????,????,????∈??????,有:
?
????????????=????????????
?
????????????????????=????????????????????????
?
????????????????=?????
?
????+????
?
探究新知
复数代数形式的乘方
实数集内的乘法、乘方的一些重要结论和运算法则在复数集内不一定成立,如:
当 ????∈???? 时, ????2=|????|2;当 ????∈???? 时, =????2∈????,????2∈????,?故 ????2 与 |????|2 不一定能比较大小
?
若 ????,????∈???? ,则 ????2+????2=0?????=????=0 ;若 ????1,????2∈?????,则 ????12+????22=0 不一定有 ????1=????2=0?,但若 ????1=????2=0?,则一定有 ????12+????22=0
?
探究新知
共轭复数的性质
设 ????=????+????????,????=?????????????,????,????∈????,????1,????2,…????????∈????,则:
?
????=????
?
????=?????????是实数
?
????=??????且?????≠?????????是纯虚数
?
????=?????????????=????
?
????+????=?????????,??????????=?????????????,????????=????????+????????
?
探究新知
复数代数形式的除法运算
定义
1
规定复数的除法是乘法的逆运算,即把满足 ????+????????????+????????=????+????????(????,????,????,????,????,????∈????,????+????????≠0) 的复数 ????+???????? 叫做复数 ????+???????? 除以复数
????+???????? 的商,记作 (????+????????)÷(????+????????) 或 ????+????????????+????????
?
复数的除法法则
2
????+????????÷????+????????=????+????????????+????????=(????+????????)(?????????????)(????+????????)(?????????????)=(????????+????????)+?????????????????????????????+????????
?
=????????+????????????????+????????+?????????????????????????+????????????(????+????????≠????)
?
由此可见,两个复数相除(除数不为0)的结果是一个确定的复数
探究新知
复数代数形式的除法运算
复数的除法与实数的除法有所不同,对于实数的除法,可以直接约分化简,得出结论;但是对于复数的除法,因为分母为复数,一般不能直接约分化简.
复数除法实质上就是分母实数化的过程.
复数的除法法则形式复杂,难于记忆,所以有关复数的除法运算,只要记住利用分母的共轭复数对分母进行“实数化”,然后结果再写成复数的代数形式 ????+????????(????,????∈????) 即可.
?
探究新知
对共轭复数的概念理解不清
【错解】对共轭复数的概念理解不清而做错
【正解】由题意得 ????=21??=2(1+????)(1??)(1+????)=?1+????
?
已知复数 ???? 满足 1?i????=2????(????是虚数单位)?,求 ????
?
所以 ????=?1?????
?
???????????+????? 的共轭复数是多少?
?
【解】 1??1+2?=(1??)(1?2????)(1+2?)(1?2????)=?1?3?5
?
所以 1??1+2? 的共轭复数为 ?1+3?5
?
题
变式训练
误用判别式解复数范围内的一元二次方程
【错解】因为方程有实数根,所以 Δ =????+2????2?42+????????≥0,
解得 ????≥23或????≤?23
?
【正解】设 ????0 是方程的实数根,代入方程并整理,得
?
已知关于 ???? 的方程 ????2+????+2????????+2+???????? 有实数根,则实数 ???? 的值是多少?
?
????02+????????0+2+2????0+????????=0
?
∴????02+????????0+2=0,2????0+????=0,
?
解得????0=2,????=?22,
?
或????0=?2,????=22,
?
所以实数 ???? 的值是 ±22
?
已知关于 ???? 的方程 ????2?6+????????+9+????????=0 有实数根,求实数 ???? 的值.
?
题
【正解】设 ????0 是方程的实数根,代入方程并整理,得
?
????02?6????0+9+?????????0????=0
?
∴????02?6????0+9=0,?????????0=0,
?
解得????0=3,????=3,
?
所以实数 ???? 的值是 3
?
由于虚数单位的特殊性,故不能用判别式判断复数范围内的一元二次方程有无实数根
变式训练
计算:(1) 1+?????(1?????)+?1+?????;
?
题①
——复数的乘除运算
【解】(1) 1+?????1?????+?1+?????
?
(2) 1+2?2+31??2+?
?
(2)1+2?2+31??2+?
?
=2+?1+?????
?
=1+????
?
=?3+4????+3(1?????)2+?=????2+?
?
=????(2?????)(2+?)(2?????)=1+2????5=15+25????
?
题②
——与共轭复数有关的运算
【解】 ????+1????·????=(1+2????+11+2????)·(1?2????)
?
若复数 ????=1+2????,其中 ???? 是虚数单位,求 ????+1????·????
?
=1+2????·1?2????+1?2????1+2????
?
=5+?3?4????5=225?45????
?
写出复数的共轭复数,利用复数的四则运算法则,将所求式子化简,最后写成 ????+????????(????,????∈????) 的形式
?
求方程 ????2?2????+5 的复数根
?
题③
——复数范围内的解一元二次方程问题(实系数)
【解】由求根公式得
?
对于实系数一元二次方程 ????????2+????????+????=0
(????≠0且????,????,????∈????),其判别式Δ=????2?4????????.
?
????=2±?162
?
=2±4?2
?
=1±2?
?
★ 当Δ>0时,方程有两个不等实根 ?????±????????????;
?
★ 当Δ=0时,方程有两个相等实根 ?????????????;
?
★ 当Δ<0时,方程有两个共轭复数根 ??????????????±?????2????
?
若关于 ???? 的方程 3+2????????2+?????????2?????1?10????=0 有实数根,求实数 ???? 的值
?
题④
——复数范围内的解一元二次方程问题(虚系数)
【解】设方程的实数根为 ????=????,
?
将方程转化为等号两边均为复数 ????+????????(????,????∈????) 的形式,确定两边复数的实部和虚部,列出方程组求解
?
则 3????2?????2?????1+2????2+?????10????=0
?
∴ 3????2?????2?????1=0,2????2+?????10=0,
?
解得 ????=11?或?????=?715
?
谢谢聆听
7.2.2 复数的乘除运算
????????????????=????????????????
?
(????????????????)????????=????????(????????????????)
?
????????????????+????????=????????????????+????????????????
?
高中数学人教A版(2019)必修 第二册
复数代数形式的乘法运算
复数的乘法法则
设 ????????=a+b?,????2=????+?????(????,????,????,????∈????) 是任意两个复数,那么它们的积
?
a+b?????+????????=????????+?????????????+?????????????+?????????????2=?????????????????+????????+????????????
?
两个复数的积仍然是一个确定的复数
在复数中,完全平方公式,平方差公
式仍然适用
可以看出,两个复数相乘,类似于两个多项式相乘,只要在所得的结果中把 ????2 换成-1,并且把实部与虚部分别合并即可.
?
探究新知
复数代数形式的乘法运算
复数乘法满足的交换律
复数的乘法满足交换律、结合律,以及对加法的分配律,则对任意的 ????1,????2,????3∈?????,有如下规律成立:
?
【计算】(7?????)(4?3????)
?
????????????????=????????????????
?
(????????????????)????????=????????(????????????????)
?
????????????????+????????=????????????????+????????????????
?
【解】(7?????)(4?3????)
?
=28?21?????4????+3????2
?
=28?25?????3
?
=25?25????
?
例题讲解
复数代数形式的乘方
复数的乘方
和实数一样,复数的乘方就是相同复数的乘积,比如: ????3 表示3个 ???? 相乘
?
1
复数乘方的运算律
2
根据复数乘法的运算律,实数范围内的正整数指数幂的运算律在复数范围内仍然成立,即对任意 ????,????1,????2∈????,????,????∈??????,有:
?
????????????=????????????
?
????????????????????=????????????????????????
?
????????????????=?????
?
????+????
?
探究新知
复数代数形式的乘方
实数集内的乘法、乘方的一些重要结论和运算法则在复数集内不一定成立,如:
当 ????∈???? 时, ????2=|????|2;当 ????∈???? 时, =????2∈????,????2∈????,?故 ????2 与 |????|2 不一定能比较大小
?
若 ????,????∈???? ,则 ????2+????2=0?????=????=0 ;若 ????1,????2∈?????,则 ????12+????22=0 不一定有 ????1=????2=0?,但若 ????1=????2=0?,则一定有 ????12+????22=0
?
探究新知
共轭复数的性质
设 ????=????+????????,????=?????????????,????,????∈????,????1,????2,…????????∈????,则:
?
????=????
?
????=?????????是实数
?
????=??????且?????≠?????????是纯虚数
?
????=?????????????=????
?
????+????=?????????,??????????=?????????????,????????=????????+????????
?
探究新知
复数代数形式的除法运算
定义
1
规定复数的除法是乘法的逆运算,即把满足 ????+????????????+????????=????+????????(????,????,????,????,????,????∈????,????+????????≠0) 的复数 ????+???????? 叫做复数 ????+???????? 除以复数
????+???????? 的商,记作 (????+????????)÷(????+????????) 或 ????+????????????+????????
?
复数的除法法则
2
????+????????÷????+????????=????+????????????+????????=(????+????????)(?????????????)(????+????????)(?????????????)=(????????+????????)+?????????????????????????????+????????
?
=????????+????????????????+????????+?????????????????????????+????????????(????+????????≠????)
?
由此可见,两个复数相除(除数不为0)的结果是一个确定的复数
探究新知
复数代数形式的除法运算
复数的除法与实数的除法有所不同,对于实数的除法,可以直接约分化简,得出结论;但是对于复数的除法,因为分母为复数,一般不能直接约分化简.
复数除法实质上就是分母实数化的过程.
复数的除法法则形式复杂,难于记忆,所以有关复数的除法运算,只要记住利用分母的共轭复数对分母进行“实数化”,然后结果再写成复数的代数形式 ????+????????(????,????∈????) 即可.
?
探究新知
对共轭复数的概念理解不清
【错解】对共轭复数的概念理解不清而做错
【正解】由题意得 ????=21??=2(1+????)(1??)(1+????)=?1+????
?
已知复数 ???? 满足 1?i????=2????(????是虚数单位)?,求 ????
?
所以 ????=?1?????
?
???????????+????? 的共轭复数是多少?
?
【解】 1??1+2?=(1??)(1?2????)(1+2?)(1?2????)=?1?3?5
?
所以 1??1+2? 的共轭复数为 ?1+3?5
?
题
变式训练
误用判别式解复数范围内的一元二次方程
【错解】因为方程有实数根,所以 Δ =????+2????2?42+????????≥0,
解得 ????≥23或????≤?23
?
【正解】设 ????0 是方程的实数根,代入方程并整理,得
?
已知关于 ???? 的方程 ????2+????+2????????+2+???????? 有实数根,则实数 ???? 的值是多少?
?
????02+????????0+2+2????0+????????=0
?
∴????02+????????0+2=0,2????0+????=0,
?
解得????0=2,????=?22,
?
或????0=?2,????=22,
?
所以实数 ???? 的值是 ±22
?
已知关于 ???? 的方程 ????2?6+????????+9+????????=0 有实数根,求实数 ???? 的值.
?
题
【正解】设 ????0 是方程的实数根,代入方程并整理,得
?
????02?6????0+9+?????????0????=0
?
∴????02?6????0+9=0,?????????0=0,
?
解得????0=3,????=3,
?
所以实数 ???? 的值是 3
?
由于虚数单位的特殊性,故不能用判别式判断复数范围内的一元二次方程有无实数根
变式训练
计算:(1) 1+?????(1?????)+?1+?????;
?
题①
——复数的乘除运算
【解】(1) 1+?????1?????+?1+?????
?
(2) 1+2?2+31??2+?
?
(2)1+2?2+31??2+?
?
=2+?1+?????
?
=1+????
?
=?3+4????+3(1?????)2+?=????2+?
?
=????(2?????)(2+?)(2?????)=1+2????5=15+25????
?
题②
——与共轭复数有关的运算
【解】 ????+1????·????=(1+2????+11+2????)·(1?2????)
?
若复数 ????=1+2????,其中 ???? 是虚数单位,求 ????+1????·????
?
=1+2????·1?2????+1?2????1+2????
?
=5+?3?4????5=225?45????
?
写出复数的共轭复数,利用复数的四则运算法则,将所求式子化简,最后写成 ????+????????(????,????∈????) 的形式
?
求方程 ????2?2????+5 的复数根
?
题③
——复数范围内的解一元二次方程问题(实系数)
【解】由求根公式得
?
对于实系数一元二次方程 ????????2+????????+????=0
(????≠0且????,????,????∈????),其判别式Δ=????2?4????????.
?
????=2±?162
?
=2±4?2
?
=1±2?
?
★ 当Δ>0时,方程有两个不等实根 ?????±????????????;
?
★ 当Δ=0时,方程有两个相等实根 ?????????????;
?
★ 当Δ<0时,方程有两个共轭复数根 ??????????????±?????2????
?
若关于 ???? 的方程 3+2????????2+?????????2?????1?10????=0 有实数根,求实数 ???? 的值
?
题④
——复数范围内的解一元二次方程问题(虚系数)
【解】设方程的实数根为 ????=????,
?
将方程转化为等号两边均为复数 ????+????????(????,????∈????) 的形式,确定两边复数的实部和虚部,列出方程组求解
?
则 3????2?????2?????1+2????2+?????10????=0
?
∴ 3????2?????2?????1=0,2????2+?????10=0,
?
解得 ????=11?或?????=?715
?
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
