7.1.1 数系的扩充和复数的概念课件(共18张PPT)
文档属性
| 名称 | 7.1.1 数系的扩充和复数的概念课件(共18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 14:28:26 | ||
图片预览





文档简介
第7章 复数
7.1.1 数系的扩充和复数的概念
高中数学人教A版(2019)必修 第二册
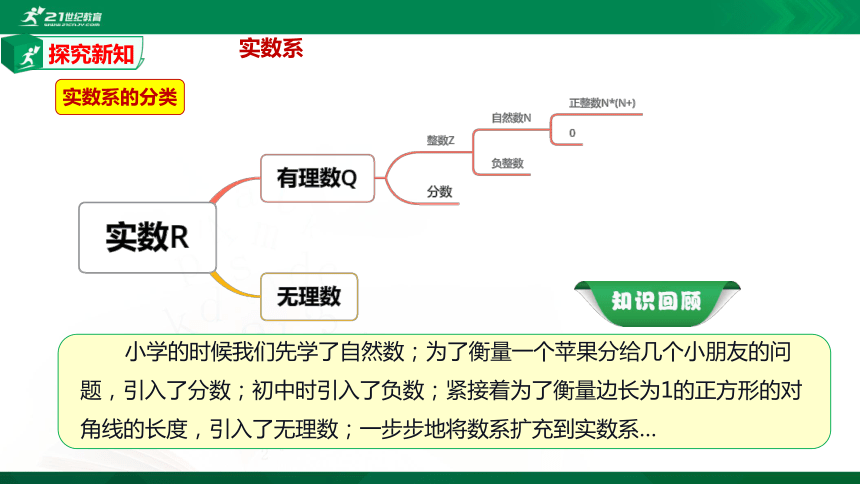
实数系
实数系的分类
小学的时候我们先学了自然数;为了衡量一个苹果分给几个小朋友的问题,引入了分数;初中时引入了负数;紧接着为了衡量边长为1的正方形的对角线的长度,引入了无理数;一步步地将数系扩充到实数系…
探究新知
实数系
实数的性质
实数对四则运算是封闭的,即两个实数进行四则运算的结果仍然是实数;
加法与乘法满足交换律、结合律,乘法对加法满足分配律;
实数和数轴上的点可以建立一 一对应的关系.
探究新知
实数的概念
复数的引入
为了解决????2+1=0这样的方程在实数系中无解的问题,设想引入一个新数?????,使得 ???? 是方程 ????2+1=0 的解,即使得 ????2=?1 ,并且 ???? 可以与实数进行四则运算,且原有的加法与乘法的运算律仍然成立.
?
1
所以实数系 ???? 经过扩容后得到的新数集是 ????={????+????????|????,????∈????}
?
(1) ????2=?1?,但并没有 ?=±?1;
?
(2) 这里只提加法与乘法运算,并没有提减法与除法,并不是复数的运算
对减法和除法不成立,而是为了后面讲复数的四则运算时,分别把减
法和除法定义为加法和乘法的逆运算.
探究新知
复数的概念
2
【1】复数:形如 ????+????????(????,????∈????) 的数叫做复数,其中 ???? 叫做虚数单位
?
复数的概念
【2】复数集:全体复数构成的集合 ????={????+????????|????,????∈????} 叫做复数集,通
常用大写字母 ???? 表示
?
【3】实部和虚部:复数通常用字母 ???? 表示,即 ????=????+????????(????,????∈????) .以后不
作特殊说明时,复数 ????=????+???????? 都有 ????,????∈???? ,其中的 ???? 与 ???? 分别叫
做复数的实部与虚部.
?
3
复数相等
在复数集 ????={????+????????|????,????∈????} 中任取两个数 ????+?????????,?????+?????????(????,????,????,????∈????) ,我们规定:????+?????????与 ????+???????? 相等,当且仅当 ????=???? 且 ????=???? .
?
探究新知
复数的概念
设复数 ????=????+????????(????,????∈????) 时,一定要有 ????,????∈???? ,否则不能说实部为 ???? ,虚部为 ???? ;
?
虚部是复数代数形式中 ???? 的实数系数,不含 ???? ,不能说虚部为 ???????? .
?
复数不能比较大小,若两个复数可以比较大小,则这两个复数必定都是实数;
????+????????=0????,????∈?????????=????=0
?
探究新知
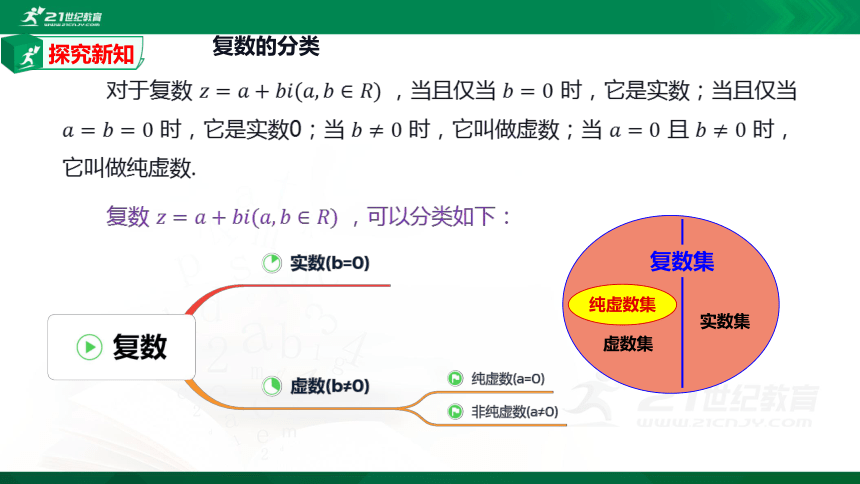
复数的分类
对于复数 ????=????+????????(????,????∈????) ,当且仅当 ????=0 时,它是实数;当且仅当 ????=????=0 时,它是实数0;当 ????≠0 时,它叫做虚数;当 ????=0 且 ????≠0 时,它叫做纯虚数.
?
复数 ????=????+????????(????,????∈????) ,可以分类如下:
?
纯虚数集
复数集
虚数集
实数集
探究新知
若复数 2?????????(????∈????) 的实部与虚部互为相反数,则 ???? 的值是多少?
?
题①
——复数的基本概念
【解】复数 2?????????(????∈????) 的实部为2,
虚部为 ?????
?
根据题意有2和 ????? 互为相反数,即
?
2+?????=0,解得????=2
?
在理解和应用复数概念时,一定要明确复数实部和虚部的定义、复数的代数形式,根据题意求出结果.
以 ?5+2???? 的虚部为实部,以 5????+2????2 的实部为虚部的复数是多少?
?
【解】复数 ?5+2???? 的虚部为 +2 , 5????+2????2=?2+5????,所以
5????+2????2 的实部为 ?2,
?
所以所求复数的实部为 +2 ,虚部为 ?2,
?
即这个复数是 2?2?????.
?
变式训练
已知复数 2?????1+????+1????=?????????+?????????????? ,其中 ????,????∈???? , ???? 为虚数单位,求实数的 ????,???? 值.
?
题②
——复数相等的充要条件
【解】∵ ????,????∈????
?
【解决复数相等问题的步骤】
① 等号两侧都写成复数的代数形式;
② 根据两个复数相等的充要条件列出方程
或者方程组;
③ 解方程或方程组,得出答案.
∴ 由复数相等的条件有
2?????1=?????????,????+1=??????????,
?
解得
????=3,????=?2.
?
【1】已知复数 2????+8????+?????6????????=14?13???? ,其中 ????,????∈???? , ???? 为虚数单位,
求实数的 ????,???? 值
?
【解】由复数相等的条件有
2????+8????=14,?????6????=?13,
?
解得????=?1,????=2.
?
【2】已知复数 ????1=2????+7+????2?2????,????2=????2?8+4????+3???? ,其中 ????∈
????,???? 为虚数单位,若,求 ???? .
?
【解】由题意有2????+7=????2?8,????2?2=4????+3,
?
即(?????5)(????+3)=0,(?????5)(????+1)=0,
?
解得 ????=5
?
变式训练
实数 ???? 分别取什么值时,复数 ????=????2??????6????+3+????2?2?????15? 是以下的数?
?
题③
——复数的分类
【解】(1) 当 ???? 满足 ????2?2?????15=0,????+3≠0, 即 ????=5 时,???? 是实数;
?
(1)实数 (2)虚数 (3)纯虚数
(2) 当 ???? 满足 ????2?2?????15≠0,????+3≠0, 即 ????≠?5 且????≠?3 时,???? 是虚数;
?
(3) 当 ???? 满足 ????2??????6????+3=0,????2?2?????15≠0,????+3≠0, 即 ????=?2 或 ????=3 时,???? 是纯虚数.
?
????: 复数 ????=????+????????(????,????∈????) 为纯虚数, ????:????=0 ,则 ???? 是 ???? 的( )
?
【解】当 ????=0 时, ????=????????(????∈????) ,若 ????=0?, ???? 不是纯虚数,所以充分性
不成立;
?
充分不必要条件
必要不充分条件
必要条件
既不充分也不必要条件
当 ????=????+????????(????,????∈????) 为纯虚数时,则 ????=0?,????≠0,所以必要性成立,故选B.
?
变式训练
已知 ????1=?4????+1+????2+3????????,????2=2????+????2+????????,其中 ????∈????,
????1>????2,求 ???? 的值.
?
题④
——复数中的比较大小
【解】 ∵ ????1>????2 ,
?
∴ ?4????+1>2????,????2+3????=0,????2+????=0,
?
解得 ????=0
?
由于出现了 ????1>????2?,即两个复数有大小关系,说明 ????1,????2 一定都是实数.解题时要善于挖掘隐含条件,也就是所谓的“坑”
?
已知复数 ????=????2??????6+????2+2?????8????(????∈????,????为虚数单位),若, ????<6 ,求实数的 ???? 值.
?
【解】因为 ????<6 ,所以 ???? 为实数,故 ????2+2?????8=0,
?
即 (?????2)(????+4)=0,解得 ????=2 或 ????=?4 .
?
当 ????=2 时, ????=22?2?6<6 成立;
?
当 ????=?4 时, ????=(?4)2?(?4)?6>6 不满足条件.
?
所以 ????=2
?
变式训练
已知 ????=????????????????+?????????????????????+?????????????????1????,A为ΔABC的一个内角,若不论A为何值, ???? 总是虚数,求实数 ???? 的取值范围.
?
题⑤
——复数的综合应用
【解】 ∵ ???? 总是虚数,
?
∴ ?????????????????????+?????????????????1≠0,即 ????≠1?????????????????????????????????
?
∵ 1?????????????????????????????????=2????????????2????22????????????????2????????????????2=????????????????2.
?
将题目中的“????总是虚数”进行转化,利用三角函数的相关性质进行求解.
?
又 ????∈0,????,所以????2∈0,????2,????????????????2∈(0,+∞)
?
所以 ????≤0 时,????≠1????????????????????????????????? 恒成立.
?
即当 ????≤0 时,不论A为何值, ???? 总是虚数
?
谢谢聆听
7.1.1 数系的扩充和复数的概念
高中数学人教A版(2019)必修 第二册
实数系
实数系的分类
小学的时候我们先学了自然数;为了衡量一个苹果分给几个小朋友的问题,引入了分数;初中时引入了负数;紧接着为了衡量边长为1的正方形的对角线的长度,引入了无理数;一步步地将数系扩充到实数系…
探究新知
实数系
实数的性质
实数对四则运算是封闭的,即两个实数进行四则运算的结果仍然是实数;
加法与乘法满足交换律、结合律,乘法对加法满足分配律;
实数和数轴上的点可以建立一 一对应的关系.
探究新知
实数的概念
复数的引入
为了解决????2+1=0这样的方程在实数系中无解的问题,设想引入一个新数?????,使得 ???? 是方程 ????2+1=0 的解,即使得 ????2=?1 ,并且 ???? 可以与实数进行四则运算,且原有的加法与乘法的运算律仍然成立.
?
1
所以实数系 ???? 经过扩容后得到的新数集是 ????={????+????????|????,????∈????}
?
(1) ????2=?1?,但并没有 ?=±?1;
?
(2) 这里只提加法与乘法运算,并没有提减法与除法,并不是复数的运算
对减法和除法不成立,而是为了后面讲复数的四则运算时,分别把减
法和除法定义为加法和乘法的逆运算.
探究新知
复数的概念
2
【1】复数:形如 ????+????????(????,????∈????) 的数叫做复数,其中 ???? 叫做虚数单位
?
复数的概念
【2】复数集:全体复数构成的集合 ????={????+????????|????,????∈????} 叫做复数集,通
常用大写字母 ???? 表示
?
【3】实部和虚部:复数通常用字母 ???? 表示,即 ????=????+????????(????,????∈????) .以后不
作特殊说明时,复数 ????=????+???????? 都有 ????,????∈???? ,其中的 ???? 与 ???? 分别叫
做复数的实部与虚部.
?
3
复数相等
在复数集 ????={????+????????|????,????∈????} 中任取两个数 ????+?????????,?????+?????????(????,????,????,????∈????) ,我们规定:????+?????????与 ????+???????? 相等,当且仅当 ????=???? 且 ????=???? .
?
探究新知
复数的概念
设复数 ????=????+????????(????,????∈????) 时,一定要有 ????,????∈???? ,否则不能说实部为 ???? ,虚部为 ???? ;
?
虚部是复数代数形式中 ???? 的实数系数,不含 ???? ,不能说虚部为 ???????? .
?
复数不能比较大小,若两个复数可以比较大小,则这两个复数必定都是实数;
????+????????=0????,????∈?????????=????=0
?
探究新知
复数的分类
对于复数 ????=????+????????(????,????∈????) ,当且仅当 ????=0 时,它是实数;当且仅当 ????=????=0 时,它是实数0;当 ????≠0 时,它叫做虚数;当 ????=0 且 ????≠0 时,它叫做纯虚数.
?
复数 ????=????+????????(????,????∈????) ,可以分类如下:
?
纯虚数集
复数集
虚数集
实数集
探究新知
若复数 2?????????(????∈????) 的实部与虚部互为相反数,则 ???? 的值是多少?
?
题①
——复数的基本概念
【解】复数 2?????????(????∈????) 的实部为2,
虚部为 ?????
?
根据题意有2和 ????? 互为相反数,即
?
2+?????=0,解得????=2
?
在理解和应用复数概念时,一定要明确复数实部和虚部的定义、复数的代数形式,根据题意求出结果.
以 ?5+2???? 的虚部为实部,以 5????+2????2 的实部为虚部的复数是多少?
?
【解】复数 ?5+2???? 的虚部为 +2 , 5????+2????2=?2+5????,所以
5????+2????2 的实部为 ?2,
?
所以所求复数的实部为 +2 ,虚部为 ?2,
?
即这个复数是 2?2?????.
?
变式训练
已知复数 2?????1+????+1????=?????????+?????????????? ,其中 ????,????∈???? , ???? 为虚数单位,求实数的 ????,???? 值.
?
题②
——复数相等的充要条件
【解】∵ ????,????∈????
?
【解决复数相等问题的步骤】
① 等号两侧都写成复数的代数形式;
② 根据两个复数相等的充要条件列出方程
或者方程组;
③ 解方程或方程组,得出答案.
∴ 由复数相等的条件有
2?????1=?????????,????+1=??????????,
?
解得
????=3,????=?2.
?
【1】已知复数 2????+8????+?????6????????=14?13???? ,其中 ????,????∈???? , ???? 为虚数单位,
求实数的 ????,???? 值
?
【解】由复数相等的条件有
2????+8????=14,?????6????=?13,
?
解得????=?1,????=2.
?
【2】已知复数 ????1=2????+7+????2?2????,????2=????2?8+4????+3???? ,其中 ????∈
????,???? 为虚数单位,若,求 ???? .
?
【解】由题意有2????+7=????2?8,????2?2=4????+3,
?
即(?????5)(????+3)=0,(?????5)(????+1)=0,
?
解得 ????=5
?
变式训练
实数 ???? 分别取什么值时,复数 ????=????2??????6????+3+????2?2?????15? 是以下的数?
?
题③
——复数的分类
【解】(1) 当 ???? 满足 ????2?2?????15=0,????+3≠0, 即 ????=5 时,???? 是实数;
?
(1)实数 (2)虚数 (3)纯虚数
(2) 当 ???? 满足 ????2?2?????15≠0,????+3≠0, 即 ????≠?5 且????≠?3 时,???? 是虚数;
?
(3) 当 ???? 满足 ????2??????6????+3=0,????2?2?????15≠0,????+3≠0, 即 ????=?2 或 ????=3 时,???? 是纯虚数.
?
????: 复数 ????=????+????????(????,????∈????) 为纯虚数, ????:????=0 ,则 ???? 是 ???? 的( )
?
【解】当 ????=0 时, ????=????????(????∈????) ,若 ????=0?, ???? 不是纯虚数,所以充分性
不成立;
?
充分不必要条件
必要不充分条件
必要条件
既不充分也不必要条件
当 ????=????+????????(????,????∈????) 为纯虚数时,则 ????=0?,????≠0,所以必要性成立,故选B.
?
变式训练
已知 ????1=?4????+1+????2+3????????,????2=2????+????2+????????,其中 ????∈????,
????1>????2,求 ???? 的值.
?
题④
——复数中的比较大小
【解】 ∵ ????1>????2 ,
?
∴ ?4????+1>2????,????2+3????=0,????2+????=0,
?
解得 ????=0
?
由于出现了 ????1>????2?,即两个复数有大小关系,说明 ????1,????2 一定都是实数.解题时要善于挖掘隐含条件,也就是所谓的“坑”
?
已知复数 ????=????2??????6+????2+2?????8????(????∈????,????为虚数单位),若, ????<6 ,求实数的 ???? 值.
?
【解】因为 ????<6 ,所以 ???? 为实数,故 ????2+2?????8=0,
?
即 (?????2)(????+4)=0,解得 ????=2 或 ????=?4 .
?
当 ????=2 时, ????=22?2?6<6 成立;
?
当 ????=?4 时, ????=(?4)2?(?4)?6>6 不满足条件.
?
所以 ????=2
?
变式训练
已知 ????=????????????????+?????????????????????+?????????????????1????,A为ΔABC的一个内角,若不论A为何值, ???? 总是虚数,求实数 ???? 的取值范围.
?
题⑤
——复数的综合应用
【解】 ∵ ???? 总是虚数,
?
∴ ?????????????????????+?????????????????1≠0,即 ????≠1?????????????????????????????????
?
∵ 1?????????????????????????????????=2????????????2????22????????????????2????????????????2=????????????????2.
?
将题目中的“????总是虚数”进行转化,利用三角函数的相关性质进行求解.
?
又 ????∈0,????,所以????2∈0,????2,????????????????2∈(0,+∞)
?
所以 ????≤0 时,????≠1????????????????????????????????? 恒成立.
?
即当 ????≤0 时,不论A为何值, ???? 总是虚数
?
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
