(新高考)热点二:多选题题型 2021届高考数学热点押题训练Word含答案
文档属性
| 名称 | (新高考)热点二:多选题题型 2021届高考数学热点押题训练Word含答案 | 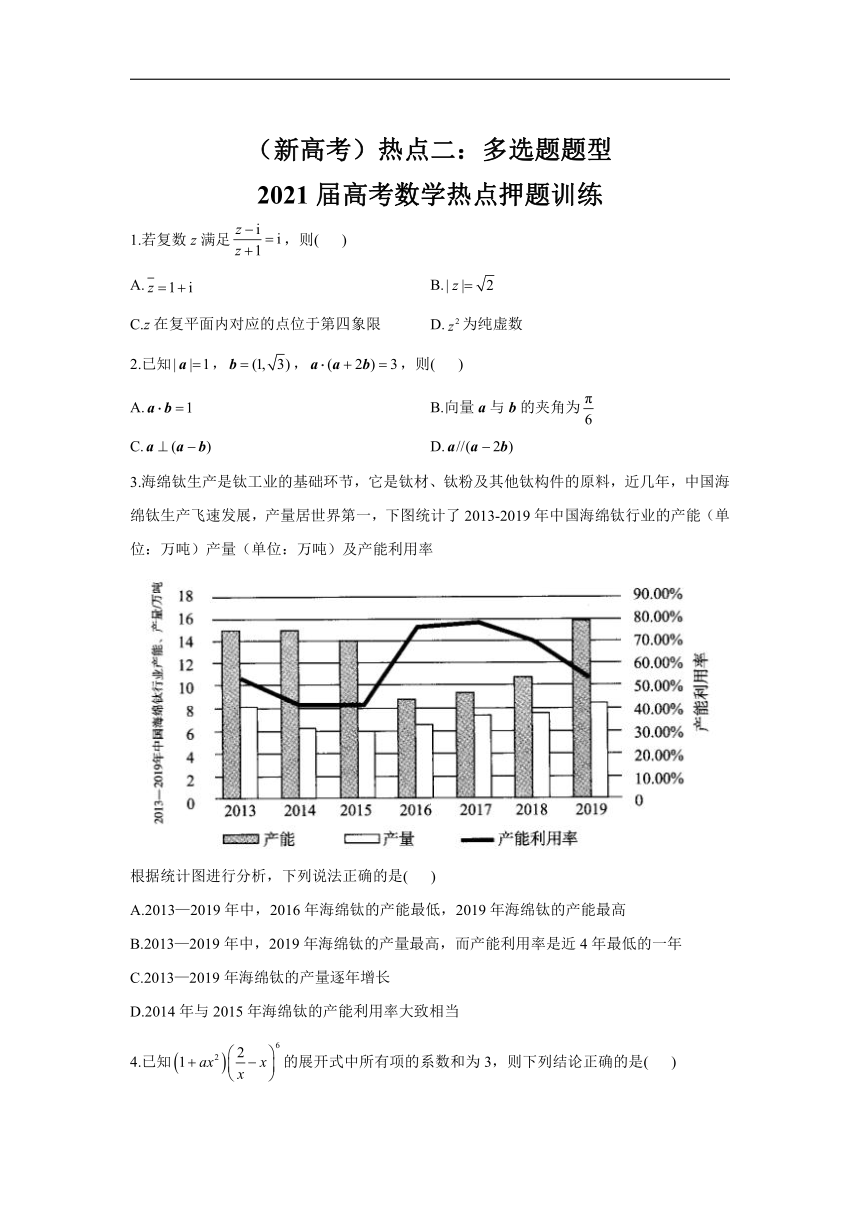 | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 21:22:58 | ||
图片预览





文档简介
(新高考)热点二:多选题题型
2021届高考数学热点押题训练
1.若复数z满足,则( )
A. B.
C.z在复平面内对应的点位于第四象限 D.为纯虚数
2.已知,,,则( )
A. B.向量a与b的夹角为
C. D.
3.海绵钛生产是钛工业的基础环节,它是钛材、钛粉及其他钛构件的原料,近几年,中国海绵钛生产飞速发展,产量居世界第一,下图统计了2013-2019年中国海绵钛行业的产能(单位:万吨)产量(单位:万吨)及产能利用率
根据统计图进行分析,下列说法正确的是( )
A.2013—2019年中,2016年海绵钛的产能最低,2019年海绵钛的产能最高
B.2013—2019年中,2019年海绵钛的产量最高,而产能利用率是近4年最低的一年
C.2013—2019年海绵钛的产量逐年增长
D.2014年与2015年海绵钛的产能利用率大致相当
4.已知的展开式中所有项的系数和为3,则下列结论正确的是( )
A.
B.展开式中的常数项为320
C.展开式中所有项的系数的绝对值的和为2187
D.展开式按x的升幂排列时第2项的系数为-192
5.已知a,b均为正实数,且,则( )
A.ab的最大值为
B.的最小值为
C.的最小值为
D.的最小值为
6.已知函数,则下列结论正确的是( )
A.是的极大值点
B.函数有且只有1个零点
C.存在正实数,使得恒成立
D.对任意两个正实数,且,若,则
7.已知函数在区间上有且仅有2个极小值点,且最多有5个零点,则下列结论正确的是( )
A.在上有且仅有2个极大值点
B.如果ω是正整数,则或5
C.的图象在上没有对称轴
D.在上单调递增
8.已知数列满足,若数列的前50项和为1273,则( )
A.是常数列
B.是常数列
C.
D.
9.已知抛物线的焦点为F,P为抛物线C上一动点,设直线l与抛物线C相交于A,B两点,点不在抛物线C上.( )
A.若直线l过点M,F且与y轴垂直,则
B.若的最小值为3,则
C.若直线l经过焦点F,则直线(O为坐标原点)的斜率满足
D.若过A,B所作的抛物线C的两条切线互相垂直,且A,B两点的纵坐标之和的最小值为2,则
10.已知函数有两个极值点,则下列说法正确的是( )
A.
B.曲线在点处的切线可能与直线垂直
C.
D.
11.已知O为坐标原点,双曲线的左、右焦点分别为,过的直线与双曲线C的左支交于A,B两点,且,为等腰直角三角形,则( )
A.
B.直线的斜率为2
C.与的面积的比值为
D. 若M为线段的中点,则的斜率
12.已知向量均为单位向量,且满足,则下列结论中正确的是( )
A.若的中点为D,则 B.为钝角
C. D.
13.设,用表示不大于x的最大整数,则称为高斯函数,也叫取整函数,下列结论正确的是( )
A.
B.
C.
D.
14.在正方体中,E是棱的中点,F在侧面上运动,且满足平面.以下命题正确的有( )
A.侧面上存在点F,使得
B.直线与直线BC所成的角可能为30°
C.平面与平面所成锐二面角的正切值为
D.设正方体的棱长为1,则过点E,F,A的平面截正方体所得截面面积的最大值为
15.下列结论正确的有( )
A.若随机变量,则
B.若,则
C.已知回归直线方程为,且,则
D.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为22
答案以及解析
1.答案:BD
解析:设则,所以解得所以,故,A错误;,B正确;z在复平面内对应点为,位于第二象限,C错误;,则为纯虚数,D正确.
2.答案:AC
解析:由,得,因为,所以,A正确;因为,所以,设向量a与b的夹角为θ,则,因为,所以,B错误;因为,所以,C正确;,所以,又,所以,所以a与不共线,D错误.
3.答案:ABD
解析:由题图易知,2016年海绵钛的产能最低,2019年海绵钛的产能最高,所以A正确;
2019年海绵钛的产量约为8.5万吨,最高,观察近4年的产能利用率易知2019年最低,所以B正确;
与2013年相比,2014年海绵钛的产量下降,所以C错误;
2014年与2015年海绵钛的产能利用率大致都在左右,所以D正确.
4.答案:BC
解析:令得的展开式中所有项的系数和为,解得,所以选项A错误;
二项式的展开式的通项,令,解得,令,解得,于是的展开式中的常数项为,所以选项B正确;
的展开式中所有项的系数的绝对值的和与的展开式中所有项的系数和相等,在中,令得,所以选项C正确;
由及的展开式可知的展开式按x的升幂排列时第2项的系数为含项的系数,令,得,令,得,则含项的系数为,所以选项D错误.故选BC.
5.答案:AC
解析:对于选项A,,当且仅当时取“=”,故A正确;对于选项B,,当且仅当时取“=”,故B错误;对于选项C,,当且仅当时取“=”,故C正确;对于选项D,,令,则,所以,当且仅当,即时取“=”,所以,当且仅当时取“=”,故选项D错误.综上选AC.
6.答案:BD
解析:,当时,;当时,.所以在上单调递减,在上单调递增,是的极小值点,故A错误.根据函数的单调性及极值点,作出函数的大致图象,如图所示,作出直线,易知直线与的图象有且只有1个交点,即函数有且只有1个零点,故B正确.若,则,令,则,令,则,所以在上单调递增,在上单调递减,,所以在上单调递减,无最小值,所以不存在正实数,使得恒成立,故C错误.由及可知,要证,即证,且在上单调递增,所以证,又,所以证,即证.令,则,所以在上单调递减,所以,所以,故D正确.故选BD.
7.答案:BC
解析:令因为所以
所以在上有且仅有2个极小值点,且最多有结合图象可知,在上有2个或3个极大值点,故A选项错误;若ω是正整数,则或5,故B选项正确;当时,因为所以故的图象在上一定没有对称轴,C选项正确;当时因为所以故在上不单调,D选项错误.
8.答案:ACD
解析:由,得,则是各项均为2的常数列,A正确;由,得,又,所以,则是以16为首项,16为公差的等差数列,B错误;数列的前50项和为
,所以,C正确;在中,令,得,又,所以,在中,令,得,所以,D正确.故选ACD.
9.答案:ACD
解析:若直线l过点M,F且与y轴垂直,则所以所以A正确.当点M在拋物线C的内部时,设是抛物线的准线,过点P作于点N,则当且仅当三点共线时等号成立,所以的最小值是由得当点M在抛物线C的外部时,连接MF,则的是小值为,所以得所以B不正确.
易知直线l的斜率存在,设直线,与联立,消去y得设则从而可得所以所以C正确.
设由得所以即所以,所以当时,取得最小值,且易得因为点所以所以D正确.故选ACD.
10.答案:ACD
解析:对于A项,由题得,令,则,令得,易得在上单调递增,在上单调递减,所以,由题意可知有两个变号零点,故,即,故A项正确;对于B项,曲线在点处的切线的斜率,若该切线与直线垂直,则,即,与矛盾,故B项不正确;对于C项,由题易知,即,则,由A项可知,所以利用二次函数的性质可得,故C项正确;对于D项,由题易知,即,则,即,要证,只需证,即证,设,则只需证,构造函数,则,所以在上单调递增,故,所以,故D项正确.故选ACD.
11.答案:AC
解析:对于选项A,令,由双曲线的定义得,所以,又为等腰直角三角形,,所以,则,A正确;对于选项B,在中,由勾股定理得,整理得,即,所以,从而直线的斜率,B错误;对于选项C,,C正确;对于选项D,设,则,两式相减,得,即,在中,由余弦定理得,即,所以,所以,从而,所以D错误.故选AC.
12.答案:ABD
解析:由于的中点为D,所以,于,即,而为单位向量,所以,故A正确;由得,于是,因此,则,所以为钝角,故B正确;,故C错误;由得,所以,于是,则,故D正确.
13.答案:BCD
解析:本题考查新定义函数问题.对于A,当a,b都是整数时,有,故A错误.对于B,因为,所以,所以,故B正确.对于C,由题意知,则只需证明成立即可,令,则,当时,,则有,那么;当时,,即,那么,所以命题成立,即,所以,故C正确.对于D,构造函数,则,所以函数是以为周期的周期函数,故只需证明在内恒成立即可,因为当时,,所以结论成立,故D正确.故选BCD.
14.答案:AC
解析:本题考查线线角、二面角、截面面积的求解、空间几何中点的轨迹问题.取的中点的中点N,连接,则易证得,由,可得平面平面,所以点F的运动轨迹为线段MN.取MN的中点F,连接,则由是等腰三角形,得.又因为,所以,故A正确;因为,所以直线与直线BC所成的角即为.当点F与点M或点N重合时,最大,此时,所以,故B错误;取F为MN的中点,连接,此时,则由平面平面,且,可得即为平面与平面所成的锐二面角,又,故C正确;当F为与MN的交点时,截面为菱形(G为的中点),其面积为,故D错误.故选AC.
15.答案:AC
解析:本题考查正态分布、二项分布、线性回归方程、统计量.选项A中,由正态分布的概率分布特点得,A正确;选项B中,由二项分布的方差公式得,则,B错误;选项C中,由线性回归方程经过样本点的中心得,解得,C正确;选项D中,设丢失的数据为x,若,则这组数据由小到大排列为x,3,3,3,5,6,11,故平均数是,中位数和众数都是3,由平均数、中位数、众数依次成等差数列得,解得,若,则这组数据由小到大排列为3,3,3,x,5,6,11,故平均数是,中位数是x,众数是3,由平均数、中位数、众数依次成等差数列得,解得,若,则这组数据的平均数是,中位数是5,众数是3,由平均数、中位数、众数依次成等差数列得,解得,故丢失数据x的所有可能值的和为,D错误,故选AC.
2021届高考数学热点押题训练
1.若复数z满足,则( )
A. B.
C.z在复平面内对应的点位于第四象限 D.为纯虚数
2.已知,,,则( )
A. B.向量a与b的夹角为
C. D.
3.海绵钛生产是钛工业的基础环节,它是钛材、钛粉及其他钛构件的原料,近几年,中国海绵钛生产飞速发展,产量居世界第一,下图统计了2013-2019年中国海绵钛行业的产能(单位:万吨)产量(单位:万吨)及产能利用率
根据统计图进行分析,下列说法正确的是( )
A.2013—2019年中,2016年海绵钛的产能最低,2019年海绵钛的产能最高
B.2013—2019年中,2019年海绵钛的产量最高,而产能利用率是近4年最低的一年
C.2013—2019年海绵钛的产量逐年增长
D.2014年与2015年海绵钛的产能利用率大致相当
4.已知的展开式中所有项的系数和为3,则下列结论正确的是( )
A.
B.展开式中的常数项为320
C.展开式中所有项的系数的绝对值的和为2187
D.展开式按x的升幂排列时第2项的系数为-192
5.已知a,b均为正实数,且,则( )
A.ab的最大值为
B.的最小值为
C.的最小值为
D.的最小值为
6.已知函数,则下列结论正确的是( )
A.是的极大值点
B.函数有且只有1个零点
C.存在正实数,使得恒成立
D.对任意两个正实数,且,若,则
7.已知函数在区间上有且仅有2个极小值点,且最多有5个零点,则下列结论正确的是( )
A.在上有且仅有2个极大值点
B.如果ω是正整数,则或5
C.的图象在上没有对称轴
D.在上单调递增
8.已知数列满足,若数列的前50项和为1273,则( )
A.是常数列
B.是常数列
C.
D.
9.已知抛物线的焦点为F,P为抛物线C上一动点,设直线l与抛物线C相交于A,B两点,点不在抛物线C上.( )
A.若直线l过点M,F且与y轴垂直,则
B.若的最小值为3,则
C.若直线l经过焦点F,则直线(O为坐标原点)的斜率满足
D.若过A,B所作的抛物线C的两条切线互相垂直,且A,B两点的纵坐标之和的最小值为2,则
10.已知函数有两个极值点,则下列说法正确的是( )
A.
B.曲线在点处的切线可能与直线垂直
C.
D.
11.已知O为坐标原点,双曲线的左、右焦点分别为,过的直线与双曲线C的左支交于A,B两点,且,为等腰直角三角形,则( )
A.
B.直线的斜率为2
C.与的面积的比值为
D. 若M为线段的中点,则的斜率
12.已知向量均为单位向量,且满足,则下列结论中正确的是( )
A.若的中点为D,则 B.为钝角
C. D.
13.设,用表示不大于x的最大整数,则称为高斯函数,也叫取整函数,下列结论正确的是( )
A.
B.
C.
D.
14.在正方体中,E是棱的中点,F在侧面上运动,且满足平面.以下命题正确的有( )
A.侧面上存在点F,使得
B.直线与直线BC所成的角可能为30°
C.平面与平面所成锐二面角的正切值为
D.设正方体的棱长为1,则过点E,F,A的平面截正方体所得截面面积的最大值为
15.下列结论正确的有( )
A.若随机变量,则
B.若,则
C.已知回归直线方程为,且,则
D.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为22
答案以及解析
1.答案:BD
解析:设则,所以解得所以,故,A错误;,B正确;z在复平面内对应点为,位于第二象限,C错误;,则为纯虚数,D正确.
2.答案:AC
解析:由,得,因为,所以,A正确;因为,所以,设向量a与b的夹角为θ,则,因为,所以,B错误;因为,所以,C正确;,所以,又,所以,所以a与不共线,D错误.
3.答案:ABD
解析:由题图易知,2016年海绵钛的产能最低,2019年海绵钛的产能最高,所以A正确;
2019年海绵钛的产量约为8.5万吨,最高,观察近4年的产能利用率易知2019年最低,所以B正确;
与2013年相比,2014年海绵钛的产量下降,所以C错误;
2014年与2015年海绵钛的产能利用率大致都在左右,所以D正确.
4.答案:BC
解析:令得的展开式中所有项的系数和为,解得,所以选项A错误;
二项式的展开式的通项,令,解得,令,解得,于是的展开式中的常数项为,所以选项B正确;
的展开式中所有项的系数的绝对值的和与的展开式中所有项的系数和相等,在中,令得,所以选项C正确;
由及的展开式可知的展开式按x的升幂排列时第2项的系数为含项的系数,令,得,令,得,则含项的系数为,所以选项D错误.故选BC.
5.答案:AC
解析:对于选项A,,当且仅当时取“=”,故A正确;对于选项B,,当且仅当时取“=”,故B错误;对于选项C,,当且仅当时取“=”,故C正确;对于选项D,,令,则,所以,当且仅当,即时取“=”,所以,当且仅当时取“=”,故选项D错误.综上选AC.
6.答案:BD
解析:,当时,;当时,.所以在上单调递减,在上单调递增,是的极小值点,故A错误.根据函数的单调性及极值点,作出函数的大致图象,如图所示,作出直线,易知直线与的图象有且只有1个交点,即函数有且只有1个零点,故B正确.若,则,令,则,令,则,所以在上单调递增,在上单调递减,,所以在上单调递减,无最小值,所以不存在正实数,使得恒成立,故C错误.由及可知,要证,即证,且在上单调递增,所以证,又,所以证,即证.令,则,所以在上单调递减,所以,所以,故D正确.故选BD.
7.答案:BC
解析:令因为所以
所以在上有且仅有2个极小值点,且最多有结合图象可知,在上有2个或3个极大值点,故A选项错误;若ω是正整数,则或5,故B选项正确;当时,因为所以故的图象在上一定没有对称轴,C选项正确;当时因为所以故在上不单调,D选项错误.
8.答案:ACD
解析:由,得,则是各项均为2的常数列,A正确;由,得,又,所以,则是以16为首项,16为公差的等差数列,B错误;数列的前50项和为
,所以,C正确;在中,令,得,又,所以,在中,令,得,所以,D正确.故选ACD.
9.答案:ACD
解析:若直线l过点M,F且与y轴垂直,则所以所以A正确.当点M在拋物线C的内部时,设是抛物线的准线,过点P作于点N,则当且仅当三点共线时等号成立,所以的最小值是由得当点M在抛物线C的外部时,连接MF,则的是小值为,所以得所以B不正确.
易知直线l的斜率存在,设直线,与联立,消去y得设则从而可得所以所以C正确.
设由得所以即所以,所以当时,取得最小值,且易得因为点所以所以D正确.故选ACD.
10.答案:ACD
解析:对于A项,由题得,令,则,令得,易得在上单调递增,在上单调递减,所以,由题意可知有两个变号零点,故,即,故A项正确;对于B项,曲线在点处的切线的斜率,若该切线与直线垂直,则,即,与矛盾,故B项不正确;对于C项,由题易知,即,则,由A项可知,所以利用二次函数的性质可得,故C项正确;对于D项,由题易知,即,则,即,要证,只需证,即证,设,则只需证,构造函数,则,所以在上单调递增,故,所以,故D项正确.故选ACD.
11.答案:AC
解析:对于选项A,令,由双曲线的定义得,所以,又为等腰直角三角形,,所以,则,A正确;对于选项B,在中,由勾股定理得,整理得,即,所以,从而直线的斜率,B错误;对于选项C,,C正确;对于选项D,设,则,两式相减,得,即,在中,由余弦定理得,即,所以,所以,从而,所以D错误.故选AC.
12.答案:ABD
解析:由于的中点为D,所以,于,即,而为单位向量,所以,故A正确;由得,于是,因此,则,所以为钝角,故B正确;,故C错误;由得,所以,于是,则,故D正确.
13.答案:BCD
解析:本题考查新定义函数问题.对于A,当a,b都是整数时,有,故A错误.对于B,因为,所以,所以,故B正确.对于C,由题意知,则只需证明成立即可,令,则,当时,,则有,那么;当时,,即,那么,所以命题成立,即,所以,故C正确.对于D,构造函数,则,所以函数是以为周期的周期函数,故只需证明在内恒成立即可,因为当时,,所以结论成立,故D正确.故选BCD.
14.答案:AC
解析:本题考查线线角、二面角、截面面积的求解、空间几何中点的轨迹问题.取的中点的中点N,连接,则易证得,由,可得平面平面,所以点F的运动轨迹为线段MN.取MN的中点F,连接,则由是等腰三角形,得.又因为,所以,故A正确;因为,所以直线与直线BC所成的角即为.当点F与点M或点N重合时,最大,此时,所以,故B错误;取F为MN的中点,连接,此时,则由平面平面,且,可得即为平面与平面所成的锐二面角,又,故C正确;当F为与MN的交点时,截面为菱形(G为的中点),其面积为,故D错误.故选AC.
15.答案:AC
解析:本题考查正态分布、二项分布、线性回归方程、统计量.选项A中,由正态分布的概率分布特点得,A正确;选项B中,由二项分布的方差公式得,则,B错误;选项C中,由线性回归方程经过样本点的中心得,解得,C正确;选项D中,设丢失的数据为x,若,则这组数据由小到大排列为x,3,3,3,5,6,11,故平均数是,中位数和众数都是3,由平均数、中位数、众数依次成等差数列得,解得,若,则这组数据由小到大排列为3,3,3,x,5,6,11,故平均数是,中位数是x,众数是3,由平均数、中位数、众数依次成等差数列得,解得,若,则这组数据的平均数是,中位数是5,众数是3,由平均数、中位数、众数依次成等差数列得,解得,故丢失数据x的所有可能值的和为,D错误,故选AC.
同课章节目录
