2020-2021学年八年级数学人教版下册第18章平行四边形单元测试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第18章平行四边形单元测试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 582.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 11:54:09 | ||
图片预览


文档简介
第18章 《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.如图,△ABC中,AC=3,BC=5,AD⊥BC交BC于点D,AD=,延长BC至E使得CE=BC,将△ABC沿AC翻折得到△AFC,连接EF,则线段EF的长为( )
A.6 B.8 C. D.
2. 如图,在矩形ABCD中,对角线AC,BD相交于点O,过O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为( )
A.12 B.18 C.24 D.30
3.已知ABCD中,∠A=4∠B,那么∠C等于( )
A.36° B.45° C.135° D.144°
4.如图,在ABC中,AB=5,AC=12,BC=13,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
A. B. C. D.
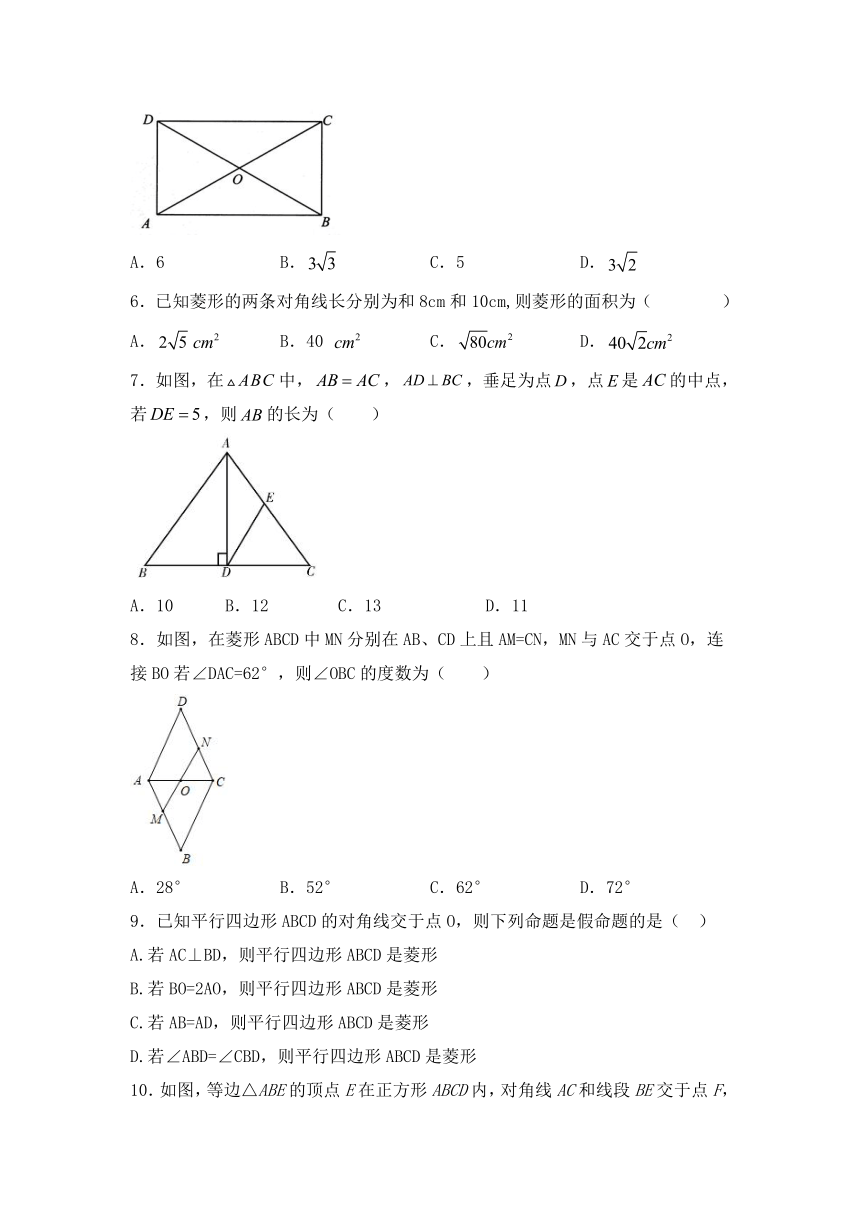
5.如图,在矩形中,,,则( )
A.6 B. C.5 D.
6.已知菱形的两条对角线长分别为和8cm和10cm,则菱形的面积为( )
A. B.40 C. D.
7.如图,在中,,,垂足为点,点是的中点,若,则的长为( )
A.10 B.12 C.13 D.11
8.如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
9.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是( )
A.若AC⊥BD,则平行四边形ABCD是菱形
B.若BO=2AO,则平行四边形ABCD是菱形
C.若AB=AD,则平行四边形ABCD是菱形
D.若∠ABD=∠CBD,则平行四边形ABCD是菱形
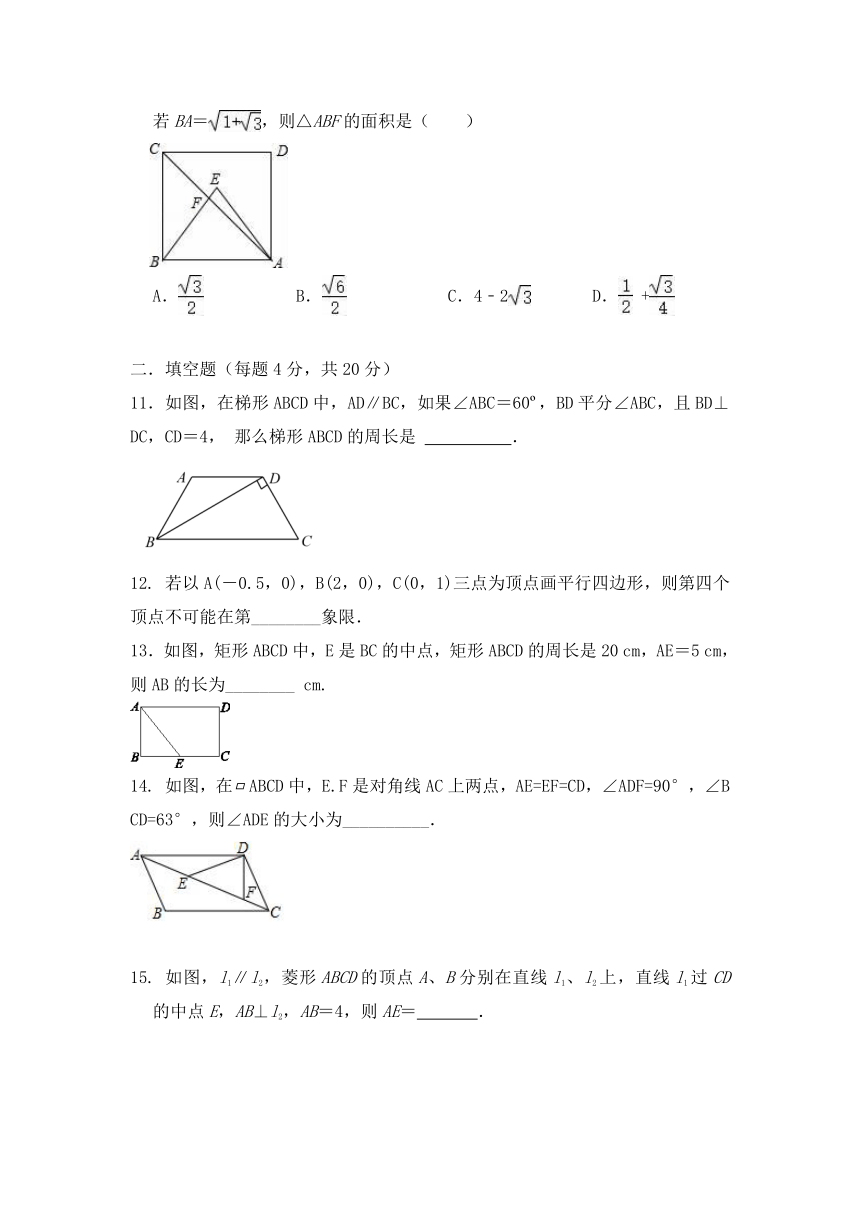
10.如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=,则△ABF的面积是( )
A. B. C.4﹣2 D. +
二.填空题(每题4分,共20分)
11.如图,在梯形ABCD中,AD∥BC,如果∠ABC=60?,BD平分∠ABC,且BD⊥DC,CD=4, 那么梯形ABCD的周长是 .
12. 若以A(-0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在第________象限.
13.如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20 cm,AE=5 cm,则AB的长为________ cm.
14. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
15. 如图,l1∥l2,菱形ABCD的顶点A、B分别在直线l1、l2上,直线l1过CD的中点E,AB⊥l2,AB=4,则AE= .
三.解答题(每题10分,共50分)
16.如图,是矩形的对角线交点,过点作分别交、于、,若,,求四边形的面积.
17.证明题:本题须有完整过程,需要括号中的理由,只限本学期所学
如图,在中,是边上的中线,,,与交于点,连接.
(1)求证:;
(2)若,求证:四边形是菱形.
18.在△ABC 中,∠BAC=90°,AD 是 BC 边上的中线,点 E 为 AD 的中点,过点 A 作 AF∥BC交 BE 的延长线于点 F,连接 CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形 ADCF 为正方形;
②连接 DF,当∠ACB= °时,四边形 ABDF 为菱形.
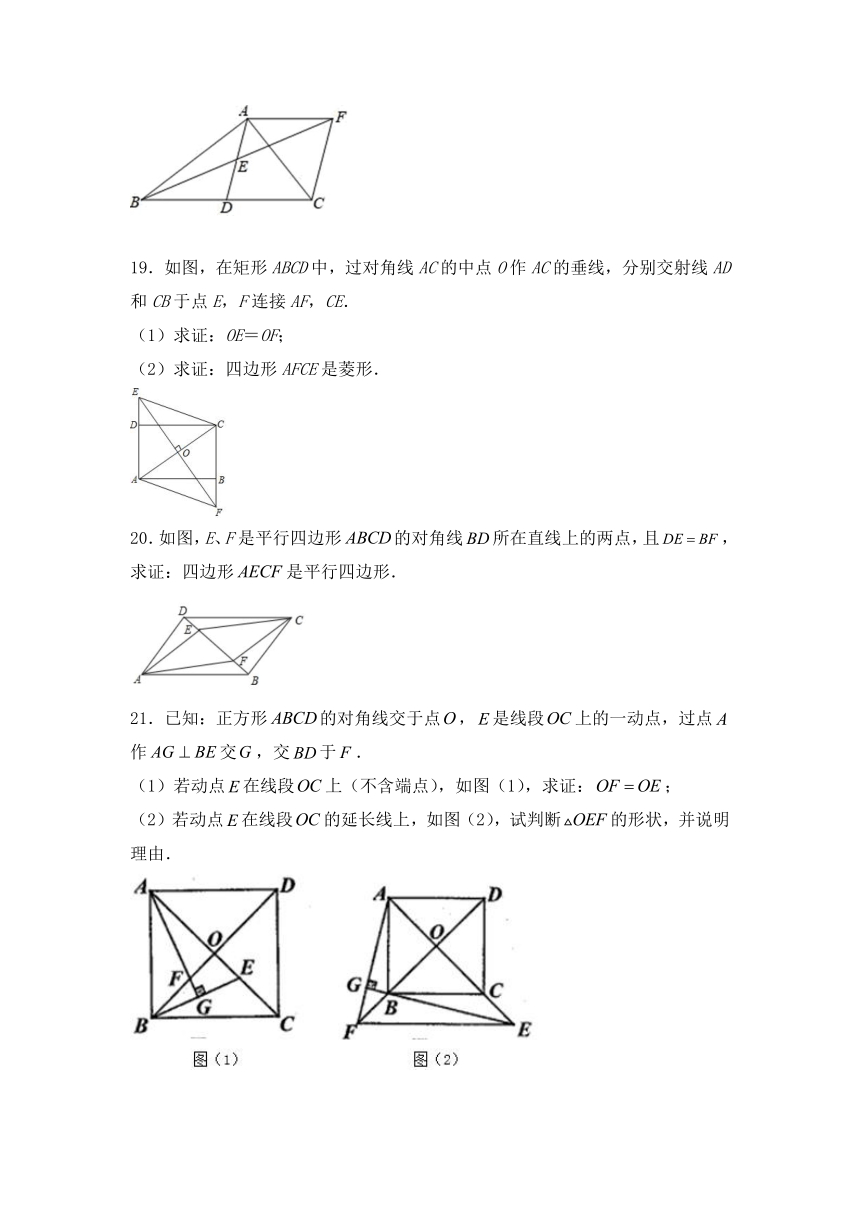
19.如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E,F连接AF,CE.
(1)求证:OE=OF;
(2)求证:四边形AFCE是菱形.
20.如图,E、F是平行四边形的对角线所在直线上的两点,且,求证:四边形是平行四边形.
21.已知:正方形的对角线交于点,是线段上的一动点,过点作交,交于.
(1)若动点在线段上(不含端点),如图(1),求证:;
(2)若动点在线段的延长线上,如图(2),试判断的形状,并说明理由.
22.如图①,在矩形中,,.点从点出发,沿运动,速度为每秒2个单位长度;点从点出发向点运动,速度为每秒1个单位长度.、两点同时出发,点运动到点时,两点同时停止运动,设点的运动时间为(秒).连结、、、.
(1)点到点时,____________;当点到终点时,的长度为_________;
(2)用含的代数式表示的长;
(3)当的面积为9时,求的值.
23.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.
24.如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4,求:
(1)AE的长;
(2)△EFC的面积.
参考答案
一.选择题
1.A 2.B 3.D 4. B. 5.A. 6.B. 7.A. 8.A.
9. B.10.C
二.填空题(共5小题)
11.20
12.三
13.4
14. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
15. 2.
三.解答题(共5小题)
16.【答案】
【解析】由为矩形可知,
又∵∥,∴
又,∴≌. 故
从而可知为菱形,∴.
又∵,
∴在直角中,由勾股定理有,
解得.故四边形的面积为()
17.解:(1)∵,
∴四边形为平行四边形(平行四边形的定义)
∴(平行四边形的两组对边分别相等)
∵是边上的中线
∴
∴
又∵
∴四边形为平行四边形(一组对边平行且相等的四边形是平行四边形)
∴(平行四边形的两组对边分别相等).
(2)∵,是边上的中线
∴
由(1)知,四边形为平行四边形
∴四边形是菱形
故答案是:(1)详见解析;(2)详见解析
18.(1)∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)①当∠ACB=45°时,四边形ADCF为正方形;
∵AD=AF,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是菱形,
要使四边形ADCF是正方形,
则∠DCF=90°,
∴∠ACD=∠ACF=45°;
②当∠ACB=30°时,四边形ABDF为菱形;
由(1)得AF=BD,AF∥BC,
∴四边形ABDF是平行四边形,
要使四边形ABDF为菱形,
∴AB=BD,
又∵AD =BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ACB=30°.
故答案为:45,30
19.解:(1)∵四边形ABCD是矩形,
∴,
∴∠EAO=∠FCO,
∵AC的中点是O,
∴OA=OC,
在和中,
,
,
∴OE=OF;
(2)∵OE=OF,AO=CO,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
20证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴(SAS),
∴,,
∵,
∴,
∴,
∴四边形是平行四边形.
21.(1)证明:∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴,
∴;
(2)解:是等腰直角三角形,理由如下:
∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴
∴;
又∵,
∴是等腰直角三角形.
22.(1),;(2)当时,;当时,;当时,;(3)当的面积为9时或.
23.【分析】(1)由平行线可得四边形OBEC为平行四边形,又矩形对角线互相平分且相等,则可得四边形OBEC为菱形;
(2)由平行线可得四边形OBEC为平行四边形,又正方形对角线互相垂直、平分且相等,则可得四边形OBEC为正方形.
【解答】解:(1)四边形OBEC是菱形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是矩形,
∴OC=OB,
∴平行四边形OBEC为菱形;
(2)四边形OBEC是正方形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是正方形,
∴OC=OB,∠BOC=90°,
∴平行四边形OBEC为正方形.
【点评】本题主要考查了平行四边形的判定,矩形、正方形的性质以及正方形、菱形的判定,应熟练掌握.
24.解:(1)
∵在?ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∵AB∥DF,AD∥BC,
∴∠BAF=∠F=∠DAF,∠BAE=∠AEB,
∴AB=BE=6,AD=DF=9,
∴△ADF是等腰三角形,△ABE是等腰三角形,
在△ABG中,BG⊥AE,AB=6,BG=4,
∴AG==2,
∴AE=2AG=4;
(2)∵AE=2AG=4,
∴△ABE的面积等于8,
∵DF∥AB,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的面积为2.
一.选择题(每题3分,共30分)
1.如图,△ABC中,AC=3,BC=5,AD⊥BC交BC于点D,AD=,延长BC至E使得CE=BC,将△ABC沿AC翻折得到△AFC,连接EF,则线段EF的长为( )
A.6 B.8 C. D.
2. 如图,在矩形ABCD中,对角线AC,BD相交于点O,过O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为( )
A.12 B.18 C.24 D.30
3.已知ABCD中,∠A=4∠B,那么∠C等于( )
A.36° B.45° C.135° D.144°
4.如图,在ABC中,AB=5,AC=12,BC=13,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
A. B. C. D.
5.如图,在矩形中,,,则( )
A.6 B. C.5 D.
6.已知菱形的两条对角线长分别为和8cm和10cm,则菱形的面积为( )
A. B.40 C. D.
7.如图,在中,,,垂足为点,点是的中点,若,则的长为( )
A.10 B.12 C.13 D.11
8.如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
9.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是( )
A.若AC⊥BD,则平行四边形ABCD是菱形
B.若BO=2AO,则平行四边形ABCD是菱形
C.若AB=AD,则平行四边形ABCD是菱形
D.若∠ABD=∠CBD,则平行四边形ABCD是菱形
10.如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=,则△ABF的面积是( )
A. B. C.4﹣2 D. +
二.填空题(每题4分,共20分)
11.如图,在梯形ABCD中,AD∥BC,如果∠ABC=60?,BD平分∠ABC,且BD⊥DC,CD=4, 那么梯形ABCD的周长是 .
12. 若以A(-0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在第________象限.
13.如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20 cm,AE=5 cm,则AB的长为________ cm.
14. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
15. 如图,l1∥l2,菱形ABCD的顶点A、B分别在直线l1、l2上,直线l1过CD的中点E,AB⊥l2,AB=4,则AE= .
三.解答题(每题10分,共50分)
16.如图,是矩形的对角线交点,过点作分别交、于、,若,,求四边形的面积.
17.证明题:本题须有完整过程,需要括号中的理由,只限本学期所学
如图,在中,是边上的中线,,,与交于点,连接.
(1)求证:;
(2)若,求证:四边形是菱形.
18.在△ABC 中,∠BAC=90°,AD 是 BC 边上的中线,点 E 为 AD 的中点,过点 A 作 AF∥BC交 BE 的延长线于点 F,连接 CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形 ADCF 为正方形;
②连接 DF,当∠ACB= °时,四边形 ABDF 为菱形.
19.如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E,F连接AF,CE.
(1)求证:OE=OF;
(2)求证:四边形AFCE是菱形.
20.如图,E、F是平行四边形的对角线所在直线上的两点,且,求证:四边形是平行四边形.
21.已知:正方形的对角线交于点,是线段上的一动点,过点作交,交于.
(1)若动点在线段上(不含端点),如图(1),求证:;
(2)若动点在线段的延长线上,如图(2),试判断的形状,并说明理由.
22.如图①,在矩形中,,.点从点出发,沿运动,速度为每秒2个单位长度;点从点出发向点运动,速度为每秒1个单位长度.、两点同时出发,点运动到点时,两点同时停止运动,设点的运动时间为(秒).连结、、、.
(1)点到点时,____________;当点到终点时,的长度为_________;
(2)用含的代数式表示的长;
(3)当的面积为9时,求的值.
23.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.
24.如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4,求:
(1)AE的长;
(2)△EFC的面积.
参考答案
一.选择题
1.A 2.B 3.D 4. B. 5.A. 6.B. 7.A. 8.A.
9. B.10.C
二.填空题(共5小题)
11.20
12.三
13.4
14. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
15. 2.
三.解答题(共5小题)
16.【答案】
【解析】由为矩形可知,
又∵∥,∴
又,∴≌. 故
从而可知为菱形,∴.
又∵,
∴在直角中,由勾股定理有,
解得.故四边形的面积为()
17.解:(1)∵,
∴四边形为平行四边形(平行四边形的定义)
∴(平行四边形的两组对边分别相等)
∵是边上的中线
∴
∴
又∵
∴四边形为平行四边形(一组对边平行且相等的四边形是平行四边形)
∴(平行四边形的两组对边分别相等).
(2)∵,是边上的中线
∴
由(1)知,四边形为平行四边形
∴四边形是菱形
故答案是:(1)详见解析;(2)详见解析
18.(1)∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)①当∠ACB=45°时,四边形ADCF为正方形;
∵AD=AF,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是菱形,
要使四边形ADCF是正方形,
则∠DCF=90°,
∴∠ACD=∠ACF=45°;
②当∠ACB=30°时,四边形ABDF为菱形;
由(1)得AF=BD,AF∥BC,
∴四边形ABDF是平行四边形,
要使四边形ABDF为菱形,
∴AB=BD,
又∵AD =BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ACB=30°.
故答案为:45,30
19.解:(1)∵四边形ABCD是矩形,
∴,
∴∠EAO=∠FCO,
∵AC的中点是O,
∴OA=OC,
在和中,
,
,
∴OE=OF;
(2)∵OE=OF,AO=CO,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
20证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴(SAS),
∴,,
∵,
∴,
∴,
∴四边形是平行四边形.
21.(1)证明:∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴,
∴;
(2)解:是等腰直角三角形,理由如下:
∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴
∴;
又∵,
∴是等腰直角三角形.
22.(1),;(2)当时,;当时,;当时,;(3)当的面积为9时或.
23.【分析】(1)由平行线可得四边形OBEC为平行四边形,又矩形对角线互相平分且相等,则可得四边形OBEC为菱形;
(2)由平行线可得四边形OBEC为平行四边形,又正方形对角线互相垂直、平分且相等,则可得四边形OBEC为正方形.
【解答】解:(1)四边形OBEC是菱形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是矩形,
∴OC=OB,
∴平行四边形OBEC为菱形;
(2)四边形OBEC是正方形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是正方形,
∴OC=OB,∠BOC=90°,
∴平行四边形OBEC为正方形.
【点评】本题主要考查了平行四边形的判定,矩形、正方形的性质以及正方形、菱形的判定,应熟练掌握.
24.解:(1)
∵在?ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∵AB∥DF,AD∥BC,
∴∠BAF=∠F=∠DAF,∠BAE=∠AEB,
∴AB=BE=6,AD=DF=9,
∴△ADF是等腰三角形,△ABE是等腰三角形,
在△ABG中,BG⊥AE,AB=6,BG=4,
∴AG==2,
∴AE=2AG=4;
(2)∵AE=2AG=4,
∴△ABE的面积等于8,
∵DF∥AB,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的面积为2.
