2020-2021学年华东师大版数学八年级下册同步训练:第18章 平行四边形自我综合评价(Word版,附答案)
文档属性
| 名称 | 2020-2021学年华东师大版数学八年级下册同步训练:第18章 平行四边形自我综合评价(Word版,附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 323.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 17:53:26 | ||
图片预览


文档简介
自我综合评价(三)
[范围:第18章 平行四边形 ]
一、选择题(每小题4分,共32分)
1.平行四边形具有而一般四边形不一定具有的性质是 ( )
A.内角和等于360° B.外角和等于360°
C.不稳定 D.对角线互相平分
2.如图,在?ABCD中,AB=3,AD=2,则CD的长为 ( )
A.3 B.2 C.1 D.5
3.在?ABCD中,若∠BAD与∠CDA的平分线交于点E,则△AED的形状是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
4.下列选项中,不能判定四边形ABCD是平行四边形的是 ( )
A.AD∥BC,AB∥CD B.AB∥CD,AB=CD
C.AD∥BC,AB=DC D.AB=DC,AD=BC
5.如图,在?ABCD中,AB=4,BC=6,对角线AC,BD相交于点O,则OA的取值范围是 ( )
A.26.如图在?ABCD中,AB=3,BC=5.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 ( )
A. B. C.1 D.2
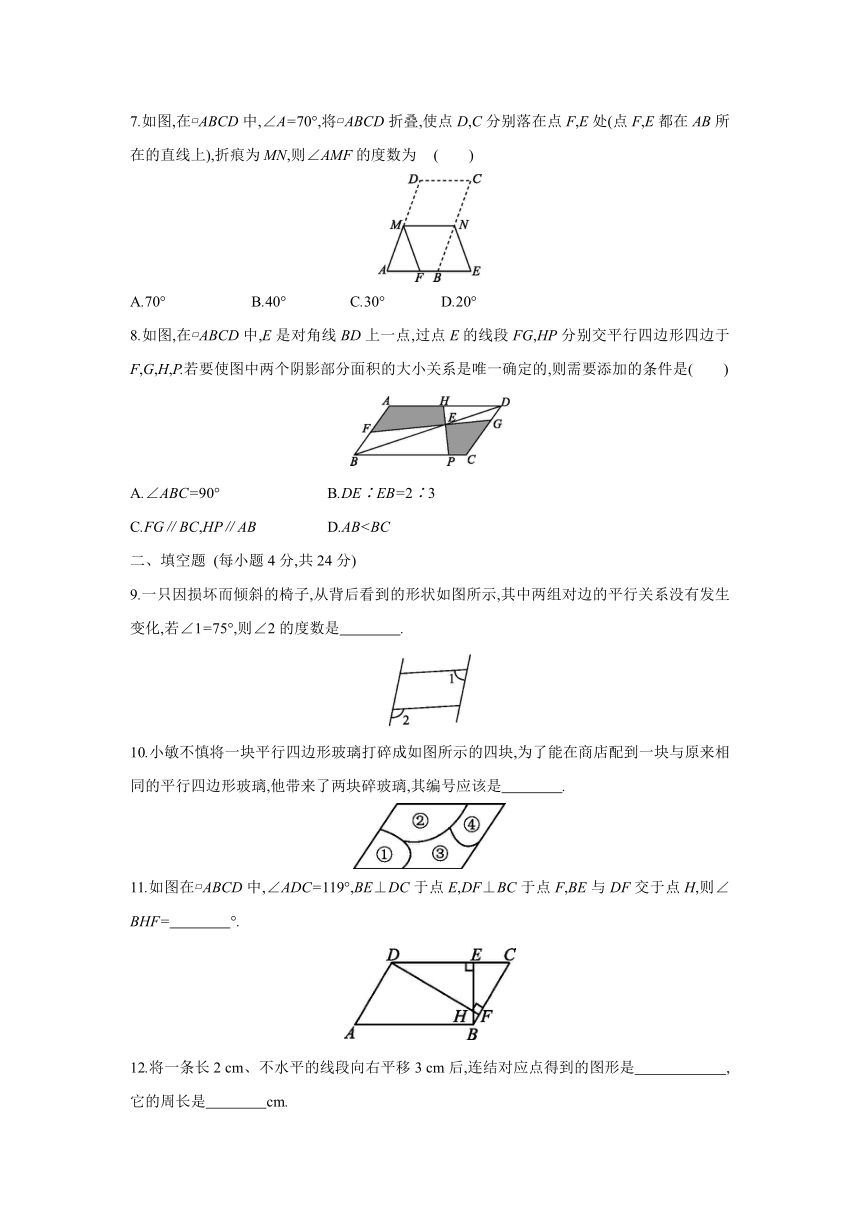
7.如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF的度数为 ( )
A.70° B.40° C.30° D.20°
8.如图,在?ABCD中,E是对角线BD上一点,过点E的线段FG,HP分别交平行四边形四边于F,G,H,P.若要使图中两个阴影部分面积的大小关系是唯一确定的,则需要添加的条件是( )
A.∠ABC=90° B.DE∶EB=2∶3
C.FG∥BC,HP∥AB D.AB二、填空题 (每小题4分,共24分)
9.一只因损坏而倾斜的椅子,从背后看到的形状如图所示,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的度数是 .?
10.小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是 .?
11.如图在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= °.?
12.将一条长2 cm、不水平的线段向右平移3 cm后,连结对应点得到的图形是 ,它的周长是 cm.?
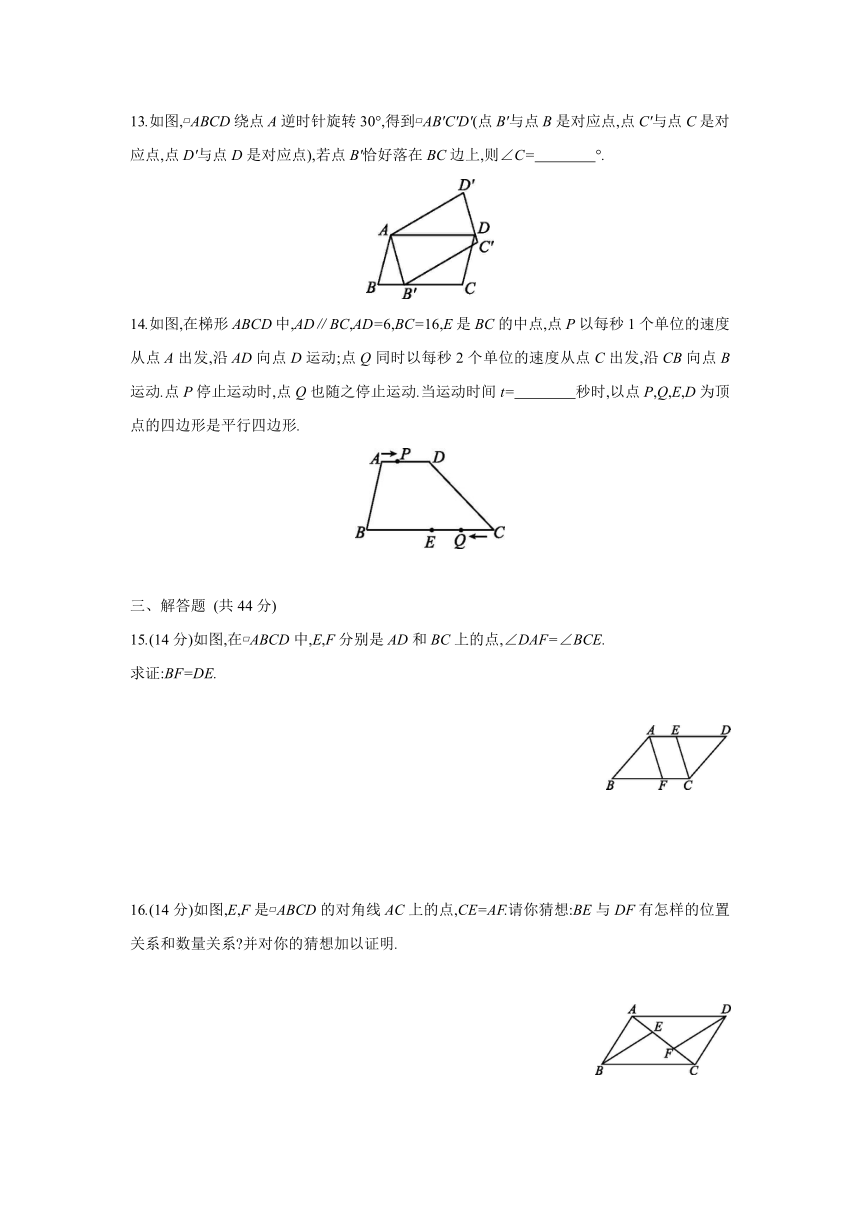
13.如图,?ABCD绕点A逆时针旋转30°,得到?AB'C'D'(点B'与点B是对应点,点C'与点C是对应点,点D'与点D是对应点),若点B'恰好落在BC边上,则∠C= °.?
14.如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t= 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.?
三、解答题 (共44分)
15.(14分)如图,在?ABCD中,E,F分别是AD和BC上的点,∠DAF=∠BCE.
求证:BF=DE.
16.(14分)如图,E,F是?ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
17.(16分)如图,在△ABC中,∠ACB=90°,AM与BN相交于点P,且BM=AC,AN=MC,△EMC是等腰直角三角形.
(1)求证:四边形MENA是平行四边形;
(2)求∠BPM的度数.
详解
作者说卷
本章在初中几何中占有很重要的地位,它是学好几何的基础.平行四边形主要包括平行四边形的判定和性质.本卷涉及的有:
类别 题号
知识与技能 平行四边形的性质 1,2,3,5,6,7,8,11,12,16
平行四边形的判定 4,9,10,14,15,17
思想方法 分类讨论思想 14
亮点 8,10
1.D
2.A
3.B [解析] 如图,∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAD+∠ADC=180°.
∵∠EAD=∠BAD,∠ADE=∠ADC,∴∠EAD+∠ADE=(∠BAD+∠ADC)=90°,
∴∠E=90°,∴△ADE是直角三角形.
4.C [解析] 一组对边平行,另一级对边相等不能判定四边形ABCD是平行四边形.故选C.
5.B [解析] ∵AB=4,BC=6,∴2∴OA=AC,∴16.D [解析] ∵由题意可知CE是∠BCD的平分线,∴∠BCE=∠DCE.∵四边形ABCD是平行四边形,∴AB∥CD,∴∠DCE=∠E,∴∠BCE=∠E,∴BE=BC=5.∵AB=3,∴AE=BE-AB=2.
故选D.
7.B [解析] 根据题意,得AM=MD=MF,
∴∠MFA=∠A=70°,∴∠AMF=180°-70°-70°=40°.故选B.
8.C [解析] 当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.
理由:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD∥BC.
∵AB∥HP,FG∥BC,
∴AD∥FG∥BC,AB∥HP∥CD,
∴∠ADB=∠DBC,四边形EFBP和四边形DHEG是平行四边形.
在△DAB和△BCD中,∵∠A=∠C,∠ADB=∠DBC,BD=DB,
∴△DAB≌△BCD(A.A.S.),
∴S△DAB=S△BCD.
同理S△DHE=S△DEG,S△EFB=S△BPE.
∵S四边形AFEH=S△ABD-S△EFB-S△DHE,S四边形EPCG=S△BCD-S△BPE-S△DEG,
∴S四边形AFEH=S四边形EPCG.
∴当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.故选C.
9.105°
10.②③ [解析] 只有②③两块角的两边互相平行,且中间部分相连,角的两边的延长线的交点就是平行四边形的顶点,∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为②③.
11.61 12.平行四边形 10
13.105 [解析] 因为旋转角是30°,所以∠BAB'=30°.因为点B'在BC上,所以AB=AB',
所以∠B=75°.因为四边形ABCD是平行四边形,所以∠B+∠C=180°,所以∠C=105°.
14. 2或 [解析] 设运动时间为t秒,如图,(1)当点Q运动到点E和点C之间时,则有-2t=6-t,解得t=2;
(2)当点Q运动到点E和点B之间时,则有2t-=6-t,解得t=.∴t=2或t=.
15.证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,∠BAD=∠BCD,AB=CD.
∵∠DAF=∠BCE,
∴∠BAF=∠DCE.
在△ABF和△CDE中,∵∠B=∠D,AB=CD,∠BAF=∠DCE,
∴△ABF≌△CDE(A.S.A.),
∴BF=DE.
16.解:猜想:BE∥DF,BE=DF.
证明:证法一:如图①.
∵四边形ABCD是平行四边形,
∴BC=AD,∠1=∠2.
又∵CE=AF,
∴△BCE≌△DAF,
∴BE=DF,∠3=∠4,∴BE∥DF.
证法二:如图②,连结BD,交AC于点O,连结DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=CO.
又∵AF=CE,
∴AE=CF,∴EO=FO,
∴四边形BEDF是平行四边形,
∴BE∥DF,BE=DF.
17.解:(1)证明:∵△EMC是等腰直角三角形,∴MC=ME,∠CME=90°.又∵∠ACB=90°,AN=MC,∴AC∥ME,AN=ME,
∴四边形MENA是平行四边形.
(2)如图,连结BE,由(1)知四边形MENA为平行四边形,∴NE=AM,∠2=∠1,AM∥NE,
∴∠3=∠BPM.
在△BEM和△AMC中,
∵ME=MC,∠BME=∠ACM=90°,BM=AC,
∴△BEM≌△AMC,∴∠4=∠AMC,BE=AM.∵∠2+∠AMC=90°,∴∠1+∠4=90°,
即∠BEN=90°.∵NE=AM,BE=AM,∴NE=BE,∴△BEN为等腰直角三角形,∠3=45°,
∴∠BPM=∠3=45°.
[范围:第18章 平行四边形 ]
一、选择题(每小题4分,共32分)
1.平行四边形具有而一般四边形不一定具有的性质是 ( )
A.内角和等于360° B.外角和等于360°
C.不稳定 D.对角线互相平分
2.如图,在?ABCD中,AB=3,AD=2,则CD的长为 ( )
A.3 B.2 C.1 D.5
3.在?ABCD中,若∠BAD与∠CDA的平分线交于点E,则△AED的形状是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
4.下列选项中,不能判定四边形ABCD是平行四边形的是 ( )
A.AD∥BC,AB∥CD B.AB∥CD,AB=CD
C.AD∥BC,AB=DC D.AB=DC,AD=BC
5.如图,在?ABCD中,AB=4,BC=6,对角线AC,BD相交于点O,则OA的取值范围是 ( )
A.2
A. B. C.1 D.2
7.如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF的度数为 ( )
A.70° B.40° C.30° D.20°
8.如图,在?ABCD中,E是对角线BD上一点,过点E的线段FG,HP分别交平行四边形四边于F,G,H,P.若要使图中两个阴影部分面积的大小关系是唯一确定的,则需要添加的条件是( )
A.∠ABC=90° B.DE∶EB=2∶3
C.FG∥BC,HP∥AB D.AB
9.一只因损坏而倾斜的椅子,从背后看到的形状如图所示,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的度数是 .?
10.小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是 .?
11.如图在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= °.?
12.将一条长2 cm、不水平的线段向右平移3 cm后,连结对应点得到的图形是 ,它的周长是 cm.?
13.如图,?ABCD绕点A逆时针旋转30°,得到?AB'C'D'(点B'与点B是对应点,点C'与点C是对应点,点D'与点D是对应点),若点B'恰好落在BC边上,则∠C= °.?
14.如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点,点P以每秒1个单位的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t= 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.?
三、解答题 (共44分)
15.(14分)如图,在?ABCD中,E,F分别是AD和BC上的点,∠DAF=∠BCE.
求证:BF=DE.
16.(14分)如图,E,F是?ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
17.(16分)如图,在△ABC中,∠ACB=90°,AM与BN相交于点P,且BM=AC,AN=MC,△EMC是等腰直角三角形.
(1)求证:四边形MENA是平行四边形;
(2)求∠BPM的度数.
详解
作者说卷
本章在初中几何中占有很重要的地位,它是学好几何的基础.平行四边形主要包括平行四边形的判定和性质.本卷涉及的有:
类别 题号
知识与技能 平行四边形的性质 1,2,3,5,6,7,8,11,12,16
平行四边形的判定 4,9,10,14,15,17
思想方法 分类讨论思想 14
亮点 8,10
1.D
2.A
3.B [解析] 如图,∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAD+∠ADC=180°.
∵∠EAD=∠BAD,∠ADE=∠ADC,∴∠EAD+∠ADE=(∠BAD+∠ADC)=90°,
∴∠E=90°,∴△ADE是直角三角形.
4.C [解析] 一组对边平行,另一级对边相等不能判定四边形ABCD是平行四边形.故选C.
5.B [解析] ∵AB=4,BC=6,∴2
故选D.
7.B [解析] 根据题意,得AM=MD=MF,
∴∠MFA=∠A=70°,∴∠AMF=180°-70°-70°=40°.故选B.
8.C [解析] 当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.
理由:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD∥BC.
∵AB∥HP,FG∥BC,
∴AD∥FG∥BC,AB∥HP∥CD,
∴∠ADB=∠DBC,四边形EFBP和四边形DHEG是平行四边形.
在△DAB和△BCD中,∵∠A=∠C,∠ADB=∠DBC,BD=DB,
∴△DAB≌△BCD(A.A.S.),
∴S△DAB=S△BCD.
同理S△DHE=S△DEG,S△EFB=S△BPE.
∵S四边形AFEH=S△ABD-S△EFB-S△DHE,S四边形EPCG=S△BCD-S△BPE-S△DEG,
∴S四边形AFEH=S四边形EPCG.
∴当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.故选C.
9.105°
10.②③ [解析] 只有②③两块角的两边互相平行,且中间部分相连,角的两边的延长线的交点就是平行四边形的顶点,∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为②③.
11.61 12.平行四边形 10
13.105 [解析] 因为旋转角是30°,所以∠BAB'=30°.因为点B'在BC上,所以AB=AB',
所以∠B=75°.因为四边形ABCD是平行四边形,所以∠B+∠C=180°,所以∠C=105°.
14. 2或 [解析] 设运动时间为t秒,如图,(1)当点Q运动到点E和点C之间时,则有-2t=6-t,解得t=2;
(2)当点Q运动到点E和点B之间时,则有2t-=6-t,解得t=.∴t=2或t=.
15.证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,∠BAD=∠BCD,AB=CD.
∵∠DAF=∠BCE,
∴∠BAF=∠DCE.
在△ABF和△CDE中,∵∠B=∠D,AB=CD,∠BAF=∠DCE,
∴△ABF≌△CDE(A.S.A.),
∴BF=DE.
16.解:猜想:BE∥DF,BE=DF.
证明:证法一:如图①.
∵四边形ABCD是平行四边形,
∴BC=AD,∠1=∠2.
又∵CE=AF,
∴△BCE≌△DAF,
∴BE=DF,∠3=∠4,∴BE∥DF.
证法二:如图②,连结BD,交AC于点O,连结DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=CO.
又∵AF=CE,
∴AE=CF,∴EO=FO,
∴四边形BEDF是平行四边形,
∴BE∥DF,BE=DF.
17.解:(1)证明:∵△EMC是等腰直角三角形,∴MC=ME,∠CME=90°.又∵∠ACB=90°,AN=MC,∴AC∥ME,AN=ME,
∴四边形MENA是平行四边形.
(2)如图,连结BE,由(1)知四边形MENA为平行四边形,∴NE=AM,∠2=∠1,AM∥NE,
∴∠3=∠BPM.
在△BEM和△AMC中,
∵ME=MC,∠BME=∠ACM=90°,BM=AC,
∴△BEM≌△AMC,∴∠4=∠AMC,BE=AM.∵∠2+∠AMC=90°,∴∠1+∠4=90°,
即∠BEN=90°.∵NE=AM,BE=AM,∴NE=BE,∴△BEN为等腰直角三角形,∠3=45°,
∴∠BPM=∠3=45°.
