人教版B版(2019)高中数学必修第四册第十一章立体几何初步11.1.3多面体与棱柱同步作业(Word含解析)
文档属性
| 名称 | 人教版B版(2019)高中数学必修第四册第十一章立体几何初步11.1.3多面体与棱柱同步作业(Word含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 166.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览



文档简介
多面体与棱柱
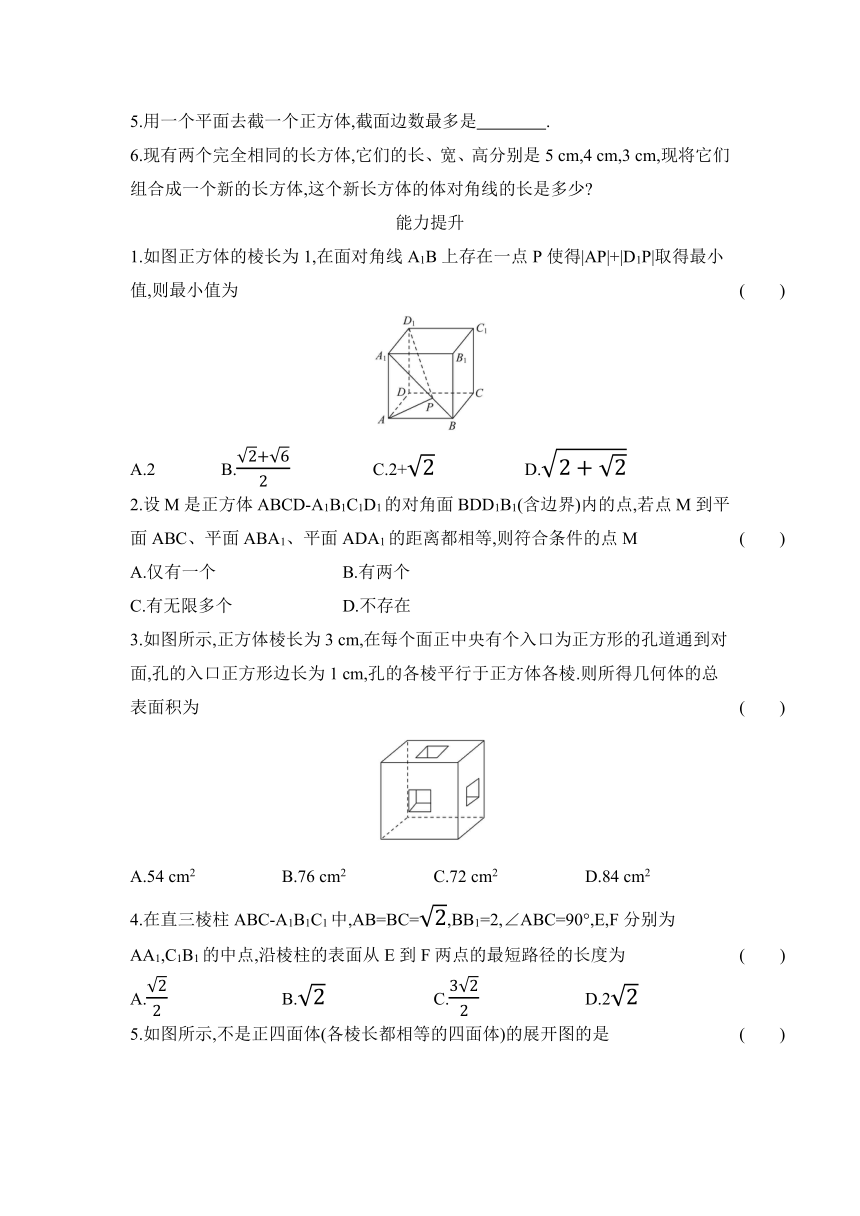
1.四棱柱有几条侧棱,几个顶点
( )
A.四条侧棱、四个顶点
B.八条侧棱、四个顶点
C.四条侧棱、八个顶点
D.六条侧棱、八个顶点
2.如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则长方体被分成的三个几何体中,棱柱的个数是
( )
A.0个
B.1个
C.2个
D.3个
3.如图所示是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点数为
( )
A.6
B.7
C.8
D.9
4.如图是一个正方体的表面展开图,若图中“努”在正方体的后面,那么这个正方体的前面是
( )
A.定
B.有
C.收
D.获
5.用一个平面去截一个正方体,截面边数最多是 .?
6.现有两个完全相同的长方体,它们的长、宽、高分别是5
cm,4
cm,3
cm,现将它们组合成一个新的长方体,这个新长方体的体对角线的长是多少?
能力提升
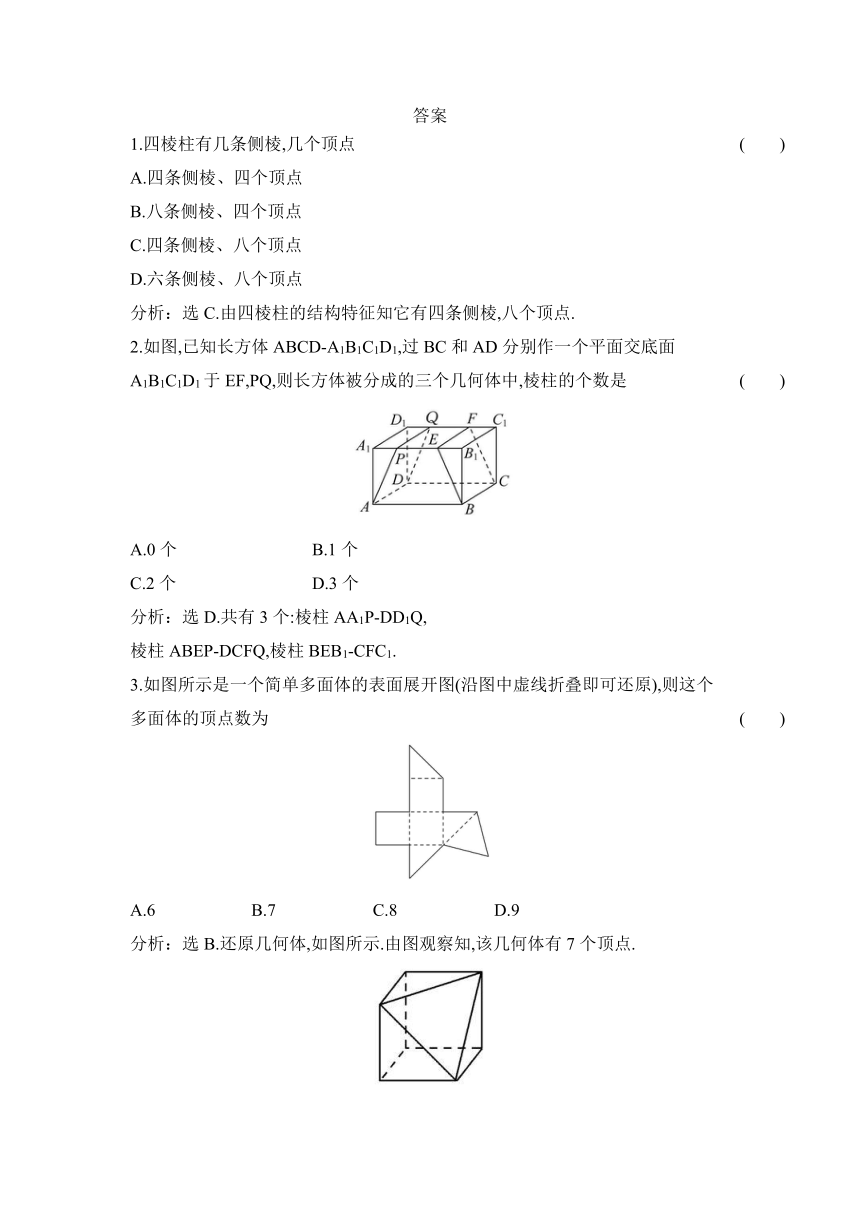
1.如图正方体的棱长为1,在面对角线A1B上存在一点P使得|AP|+|D1P|取得最小值,则最小值为
( )
A.2
B.
C.2+
D.
2.设M是正方体ABCD-A1B1C1D1的对角面BDD1B1(含边界)内的点,若点M到平面ABC、平面ABA1、平面ADA1的距离都相等,则符合条件的点M
( )
A.仅有一个
B.有两个
C.有无限多个
D.不存在
3.如图所示,正方体棱长为3
cm,在每个面正中央有个入口为正方形的孔道通到对面,孔的入口正方形边长为1
cm,孔的各棱平行于正方体各棱.则所得几何体的总表面积为
( )
A.54
cm2
B.76
cm2
C.72
cm2
D.84
cm2
4.在直三棱柱ABC-A1B1C1中,AB=BC=,BB1=2,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
( )
A.
B.
C.
D.2
5.如图所示,不是正四面体(各棱长都相等的四面体)的展开图的是
( )
6.正方体ABCD-A1B1C1D1的棱长为2,已知平面α⊥AC1,则关于α截此正方体所得截面的判断正确的是
( )
A.截面形状可能为正三角形
B.截面形状可能为正方形
C.截面形状可能为正六边形
D.截面面积最大值为3
7.侧棱垂直于底面的棱柱称为直棱柱.
侧棱不垂直于底面的棱柱称为斜棱柱.
底面是正多边形的直棱柱称为正棱柱.
底面是平行四边形的四棱柱称为平行六面体.
侧棱与底面垂直的平行六面体称为直平行六面体.
底面是矩形的直平行六面体称为长方体.
棱长都相等的长方体称为正方体.
请根据上述定义,回答下面的问题:
(1)直四棱柱 是长方体.?
(2)正四棱柱 是正方体.(填“一定”“不一定”或“一定不”)?
8.正方体的棱长为a,且正方体各面的中心是一个几何体的顶点,这个几何体的棱长为 .?
9.已知正六棱柱的一条最长的体对角线长是13,侧面积为180,求正六棱柱的全面积.
10.直四棱柱的底面是矩形,且底面对角线的夹角为60°,对角面的面积为S,求此直四棱柱的侧面积.
答案
1.四棱柱有几条侧棱,几个顶点
( )
A.四条侧棱、四个顶点
B.八条侧棱、四个顶点
C.四条侧棱、八个顶点
D.六条侧棱、八个顶点
分析:选C.由四棱柱的结构特征知它有四条侧棱,八个顶点.
2.如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则长方体被分成的三个几何体中,棱柱的个数是
( )
A.0个
B.1个
C.2个
D.3个
分析:选D.共有3个:棱柱AA1P-DD1Q,
棱柱ABEP-DCFQ,棱柱BEB1-CFC1.
3.如图所示是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点数为
( )
A.6
B.7
C.8
D.9
分析:选B.还原几何体,如图所示.由图观察知,该几何体有7个顶点.
4.如图是一个正方体的表面展开图,若图中“努”在正方体的后面,那么这个正方体的前面是
( )
A.定
B.有
C.收
D.获
分析:选B.这是一个正方体的表面展开图,共有六个面,其中面“努”与面“有”相对,
所以图中“努”在正方体的后面,则这个正方体的前面是“有”.
5.用一个平面去截一个正方体,截面边数最多是 .?
分析:因为用平面去截正方体时,最多与六个面相交得六边形,即截面的边数最多为6.
答案:6
6.现有两个完全相同的长方体,它们的长、宽、高分别是5
cm,4
cm,3
cm,现将它们组合成一个新的长方体,这个新长方体的体对角线的长是多少?
分析:将两个完全相同的长方体组合成新长方体,其情形有以下几种:将面积为5×3=15(cm2)的面重叠到一起,将面积为5×4=20(cm2)的面重叠到一起,将面积为4×3=12(cm2)的面重叠到一起.
三种情形下的体对角线分别为:l1==
7(cm),l2==(cm),l3==5(cm).
能力提升
1.如图正方体的棱长为1,在面对角线A1B上存在一点P使得|AP|+|D1P|取得最小值,则最小值为
( )
A.2
B.
C.2+
D.
分析:选D.如图所示,将平面A1BCD1绕A1B旋转至A1ABB1,连接AD1交A1B于P,
则|AD1|==.
2.设M是正方体ABCD-A1B1C1D1的对角面BDD1B1(含边界)内的点,若点M到平面ABC、平面ABA1、平面ADA1的距离都相等,则符合条件的点M
( )
A.仅有一个
B.有两个
C.有无限多个
D.不存在
分析:选A.由点M是正方体ABCD-A1B1C1D1的对角面BDD1B1(含边界)内的点,
若点M到平面ABC、平面ABA1、平面ADA1的距离都相等,
则符合条件的点M只能为正方体ABCD-A1B1C1D1的中心.
3.如图所示,正方体棱长为3
cm,在每个面正中央有个入口为正方形的孔道通到对面,孔的入口正方形边长为1
cm,孔的各棱平行于正方体各棱.则所得几何体的总表面积为
( )
A.54
cm2
B.76
cm2
C.72
cm2
D.84
cm2
分析:选C.由题意知该几何体的总表面积包含外部表面积与内部表面积.
S外=6×32-6×12=48(cm2),S内=4×6=24(cm2).
所以S总=48+24=72(cm2).
4.在直三棱柱ABC-A1B1C1中,AB=BC=,BB1=2,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
( )
A.
B.
C.
D.2
分析:选C.由题意得直三棱柱底面为等腰直角三角形.
①若把平面ABB1A1和平面B1C1CB展开在同一个平面内,则线段EF在直角三角形A1EF中,由勾股定理得EF===.
②若把平面ABB1A1和平面A1B1C1展开在同一个平面内,设BB1的中点为G,在直角三角形EFG中,由勾股定理得EF===.
③若把平面ACC1A1和平面A1B1C1展开在同一个平面内,过F作与CC1平行的直线,过E作与AC平行的直线,所作两线交于点H,则EF在直角三角形EFH中,由勾股定理得EF===.
综上可得从E到F两点的最短路径的长度为.
5.如图所示,不是正四面体(各棱长都相等的四面体)的展开图的是
( )
分析:选CD.可选择阴影三角形作为底面进行折叠,发现A,B可折成正四面体,C,D不论选哪一个三角形作底面折叠都不能折成正四面体.
6.正方体ABCD-A1B1C1D1的棱长为2,已知平面α⊥AC1,则关于α截此正方体所得截面的判断正确的是
( )
A.截面形状可能为正三角形
B.截面形状可能为正方形
C.截面形状可能为正六边形
D.截面面积最大值为3
分析:选ACD.如图,显然A,C成立,下面说明D成立,如图设截面为多边形GMEFNH,
设A1G=x,则0≤x≤1,
则GH=ME=NF=x,MG=HN=EF=(2-x),MN=2,
所以多边形GMEFNH的面积为两个等腰梯形的面积和,
所以S=·(GH+MN)·h1+·(MN+EF)·h2,
因为h1=
=,
h2==,
所以S=(x+2)·+[2+(2-x)]·=-x2+2x+2.
当x=1时,Smax=3,故D成立.
7.侧棱垂直于底面的棱柱称为直棱柱.
侧棱不垂直于底面的棱柱称为斜棱柱.
底面是正多边形的直棱柱称为正棱柱.
底面是平行四边形的四棱柱称为平行六面体.
侧棱与底面垂直的平行六面体称为直平行六面体.
底面是矩形的直平行六面体称为长方体.
棱长都相等的长方体称为正方体.
请根据上述定义,回答下面的问题:
(1)直四棱柱 是长方体.?
(2)正四棱柱 是正方体.(填“一定”“不一定”或“一定不”)?
分析:由直四棱柱的定义可知,直四棱柱不一定是长方体;长方体一定是直四棱柱;
由正四棱柱的定义可知,正四棱柱不一定是正方体;正方体一定是正四棱柱.
答案:(1)不一定 (2)不一定
8.正方体的棱长为a,且正方体各面的中心是一个几何体的顶点,这个几何体的棱长为 .?
分析:如图所示,取棱中点O,连接OD,OE,由正方体的性质可得OD⊥OE,OD=OE=a,
则DE==a,即几何体的棱长为a.
答案:a
9.已知正六棱柱的一条最长的体对角线长是13,侧面积为180,求正六棱柱的全面积.
分析:如图所示,设正六棱柱的底面边长为a,侧棱长为h,易知CF′是正六棱柱的一条最长的体对角线,即CF′=13.
因为CF=2a,FF′=h,
所以CF′===13.①
因为正六棱柱的侧面积为180,
所以S侧=6a·h=180.②
联立①②解得,或.
当a=6,h=5时,2S底=6×a2×2=108.
所以S全=180+108.
当a=,h=12时,2S底=6×a2×2=,
所以S全=180+.
10.直四棱柱的底面是矩形,且底面对角线的夹角为60°,对角面的面积为S,求此直四棱柱的侧面积.
分析:如图所示,设侧棱长为l,底面对角线长为t,则AC=BD=t,
设AC与BD相交于O点,则∠AOD=60°,∠AOB=120°,所以△AOD是等边三角形.
所以AD=OA=AC=t.
所以△AOB是顶角为120°的等腰三角形,AB=OA=t.又因为对角面的面积为S,S=t·l,
所以t=.所以AD=t=,AB=t=.
所以S侧=2(AD+AB)l=l=(+1)S.
1.四棱柱有几条侧棱,几个顶点
( )
A.四条侧棱、四个顶点
B.八条侧棱、四个顶点
C.四条侧棱、八个顶点
D.六条侧棱、八个顶点
2.如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则长方体被分成的三个几何体中,棱柱的个数是
( )
A.0个
B.1个
C.2个
D.3个
3.如图所示是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点数为
( )
A.6
B.7
C.8
D.9
4.如图是一个正方体的表面展开图,若图中“努”在正方体的后面,那么这个正方体的前面是
( )
A.定
B.有
C.收
D.获
5.用一个平面去截一个正方体,截面边数最多是 .?
6.现有两个完全相同的长方体,它们的长、宽、高分别是5
cm,4
cm,3
cm,现将它们组合成一个新的长方体,这个新长方体的体对角线的长是多少?
能力提升
1.如图正方体的棱长为1,在面对角线A1B上存在一点P使得|AP|+|D1P|取得最小值,则最小值为
( )
A.2
B.
C.2+
D.
2.设M是正方体ABCD-A1B1C1D1的对角面BDD1B1(含边界)内的点,若点M到平面ABC、平面ABA1、平面ADA1的距离都相等,则符合条件的点M
( )
A.仅有一个
B.有两个
C.有无限多个
D.不存在
3.如图所示,正方体棱长为3
cm,在每个面正中央有个入口为正方形的孔道通到对面,孔的入口正方形边长为1
cm,孔的各棱平行于正方体各棱.则所得几何体的总表面积为
( )
A.54
cm2
B.76
cm2
C.72
cm2
D.84
cm2
4.在直三棱柱ABC-A1B1C1中,AB=BC=,BB1=2,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
( )
A.
B.
C.
D.2
5.如图所示,不是正四面体(各棱长都相等的四面体)的展开图的是
( )
6.正方体ABCD-A1B1C1D1的棱长为2,已知平面α⊥AC1,则关于α截此正方体所得截面的判断正确的是
( )
A.截面形状可能为正三角形
B.截面形状可能为正方形
C.截面形状可能为正六边形
D.截面面积最大值为3
7.侧棱垂直于底面的棱柱称为直棱柱.
侧棱不垂直于底面的棱柱称为斜棱柱.
底面是正多边形的直棱柱称为正棱柱.
底面是平行四边形的四棱柱称为平行六面体.
侧棱与底面垂直的平行六面体称为直平行六面体.
底面是矩形的直平行六面体称为长方体.
棱长都相等的长方体称为正方体.
请根据上述定义,回答下面的问题:
(1)直四棱柱 是长方体.?
(2)正四棱柱 是正方体.(填“一定”“不一定”或“一定不”)?
8.正方体的棱长为a,且正方体各面的中心是一个几何体的顶点,这个几何体的棱长为 .?
9.已知正六棱柱的一条最长的体对角线长是13,侧面积为180,求正六棱柱的全面积.
10.直四棱柱的底面是矩形,且底面对角线的夹角为60°,对角面的面积为S,求此直四棱柱的侧面积.
答案
1.四棱柱有几条侧棱,几个顶点
( )
A.四条侧棱、四个顶点
B.八条侧棱、四个顶点
C.四条侧棱、八个顶点
D.六条侧棱、八个顶点
分析:选C.由四棱柱的结构特征知它有四条侧棱,八个顶点.
2.如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则长方体被分成的三个几何体中,棱柱的个数是
( )
A.0个
B.1个
C.2个
D.3个
分析:选D.共有3个:棱柱AA1P-DD1Q,
棱柱ABEP-DCFQ,棱柱BEB1-CFC1.
3.如图所示是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点数为
( )
A.6
B.7
C.8
D.9
分析:选B.还原几何体,如图所示.由图观察知,该几何体有7个顶点.
4.如图是一个正方体的表面展开图,若图中“努”在正方体的后面,那么这个正方体的前面是
( )
A.定
B.有
C.收
D.获
分析:选B.这是一个正方体的表面展开图,共有六个面,其中面“努”与面“有”相对,
所以图中“努”在正方体的后面,则这个正方体的前面是“有”.
5.用一个平面去截一个正方体,截面边数最多是 .?
分析:因为用平面去截正方体时,最多与六个面相交得六边形,即截面的边数最多为6.
答案:6
6.现有两个完全相同的长方体,它们的长、宽、高分别是5
cm,4
cm,3
cm,现将它们组合成一个新的长方体,这个新长方体的体对角线的长是多少?
分析:将两个完全相同的长方体组合成新长方体,其情形有以下几种:将面积为5×3=15(cm2)的面重叠到一起,将面积为5×4=20(cm2)的面重叠到一起,将面积为4×3=12(cm2)的面重叠到一起.
三种情形下的体对角线分别为:l1==
7(cm),l2==(cm),l3==5(cm).
能力提升
1.如图正方体的棱长为1,在面对角线A1B上存在一点P使得|AP|+|D1P|取得最小值,则最小值为
( )
A.2
B.
C.2+
D.
分析:选D.如图所示,将平面A1BCD1绕A1B旋转至A1ABB1,连接AD1交A1B于P,
则|AD1|==.
2.设M是正方体ABCD-A1B1C1D1的对角面BDD1B1(含边界)内的点,若点M到平面ABC、平面ABA1、平面ADA1的距离都相等,则符合条件的点M
( )
A.仅有一个
B.有两个
C.有无限多个
D.不存在
分析:选A.由点M是正方体ABCD-A1B1C1D1的对角面BDD1B1(含边界)内的点,
若点M到平面ABC、平面ABA1、平面ADA1的距离都相等,
则符合条件的点M只能为正方体ABCD-A1B1C1D1的中心.
3.如图所示,正方体棱长为3
cm,在每个面正中央有个入口为正方形的孔道通到对面,孔的入口正方形边长为1
cm,孔的各棱平行于正方体各棱.则所得几何体的总表面积为
( )
A.54
cm2
B.76
cm2
C.72
cm2
D.84
cm2
分析:选C.由题意知该几何体的总表面积包含外部表面积与内部表面积.
S外=6×32-6×12=48(cm2),S内=4×6=24(cm2).
所以S总=48+24=72(cm2).
4.在直三棱柱ABC-A1B1C1中,AB=BC=,BB1=2,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
( )
A.
B.
C.
D.2
分析:选C.由题意得直三棱柱底面为等腰直角三角形.
①若把平面ABB1A1和平面B1C1CB展开在同一个平面内,则线段EF在直角三角形A1EF中,由勾股定理得EF===.
②若把平面ABB1A1和平面A1B1C1展开在同一个平面内,设BB1的中点为G,在直角三角形EFG中,由勾股定理得EF===.
③若把平面ACC1A1和平面A1B1C1展开在同一个平面内,过F作与CC1平行的直线,过E作与AC平行的直线,所作两线交于点H,则EF在直角三角形EFH中,由勾股定理得EF===.
综上可得从E到F两点的最短路径的长度为.
5.如图所示,不是正四面体(各棱长都相等的四面体)的展开图的是
( )
分析:选CD.可选择阴影三角形作为底面进行折叠,发现A,B可折成正四面体,C,D不论选哪一个三角形作底面折叠都不能折成正四面体.
6.正方体ABCD-A1B1C1D1的棱长为2,已知平面α⊥AC1,则关于α截此正方体所得截面的判断正确的是
( )
A.截面形状可能为正三角形
B.截面形状可能为正方形
C.截面形状可能为正六边形
D.截面面积最大值为3
分析:选ACD.如图,显然A,C成立,下面说明D成立,如图设截面为多边形GMEFNH,
设A1G=x,则0≤x≤1,
则GH=ME=NF=x,MG=HN=EF=(2-x),MN=2,
所以多边形GMEFNH的面积为两个等腰梯形的面积和,
所以S=·(GH+MN)·h1+·(MN+EF)·h2,
因为h1=
=,
h2==,
所以S=(x+2)·+[2+(2-x)]·=-x2+2x+2.
当x=1时,Smax=3,故D成立.
7.侧棱垂直于底面的棱柱称为直棱柱.
侧棱不垂直于底面的棱柱称为斜棱柱.
底面是正多边形的直棱柱称为正棱柱.
底面是平行四边形的四棱柱称为平行六面体.
侧棱与底面垂直的平行六面体称为直平行六面体.
底面是矩形的直平行六面体称为长方体.
棱长都相等的长方体称为正方体.
请根据上述定义,回答下面的问题:
(1)直四棱柱 是长方体.?
(2)正四棱柱 是正方体.(填“一定”“不一定”或“一定不”)?
分析:由直四棱柱的定义可知,直四棱柱不一定是长方体;长方体一定是直四棱柱;
由正四棱柱的定义可知,正四棱柱不一定是正方体;正方体一定是正四棱柱.
答案:(1)不一定 (2)不一定
8.正方体的棱长为a,且正方体各面的中心是一个几何体的顶点,这个几何体的棱长为 .?
分析:如图所示,取棱中点O,连接OD,OE,由正方体的性质可得OD⊥OE,OD=OE=a,
则DE==a,即几何体的棱长为a.
答案:a
9.已知正六棱柱的一条最长的体对角线长是13,侧面积为180,求正六棱柱的全面积.
分析:如图所示,设正六棱柱的底面边长为a,侧棱长为h,易知CF′是正六棱柱的一条最长的体对角线,即CF′=13.
因为CF=2a,FF′=h,
所以CF′===13.①
因为正六棱柱的侧面积为180,
所以S侧=6a·h=180.②
联立①②解得,或.
当a=6,h=5时,2S底=6×a2×2=108.
所以S全=180+108.
当a=,h=12时,2S底=6×a2×2=,
所以S全=180+.
10.直四棱柱的底面是矩形,且底面对角线的夹角为60°,对角面的面积为S,求此直四棱柱的侧面积.
分析:如图所示,设侧棱长为l,底面对角线长为t,则AC=BD=t,
设AC与BD相交于O点,则∠AOD=60°,∠AOB=120°,所以△AOD是等边三角形.
所以AD=OA=AC=t.
所以△AOB是顶角为120°的等腰三角形,AB=OA=t.又因为对角面的面积为S,S=t·l,
所以t=.所以AD=t=,AB=t=.
所以S侧=2(AD+AB)l=l=(+1)S.
