5.1复数的概念及其几何意义-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(37张PPT)
文档属性
| 名称 | 5.1复数的概念及其几何意义-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览










文档简介
复数的概念及其几何意义
授课教师:
温故知新
学习目标
1.掌握复数的有关概念,如虚数单位、实部、
虚部、虚数、纯虚数;正确对复数进行分类,
掌握数集之间的从属关系;(重点)
2.理解复平面的实轴、虚轴、复数的模、共轭复
数的概念;(重点)
3.掌握复数的代数表示及其几何意义.(难点)
课文精讲
在数自身的发展中,求解方程是数系扩充
的重要动力.比如,要使像2x=1这样的线性方
程有解,就需要引进有理数;无理数与有理数
构成实数.
然而,即使实数也无法完全满足求解二
次方程的需要. 像x2=?1这样一个简单的方程就
没有实数解,因为任意实数的平方都不可能是
负数.
?
复数的概念
课文精讲
为此,人们开始引进一个新数i,叫作虚
数单位,并规定:
(1)它的平方等于-1,即i2=?1;
(2)实数与它进行四则运算时,原有的加法、
乘法运算律仍然成立.
?
复数的概念
课文精讲
形如a+bi(其中a,b∈R)的数叫作复数,
通常用字母z表示,即z=a+bi (a,b∈R),其
a称为复数z的实部,记作Re z,b称为复数z的
虚部,记作Im z.
对于复数a+bi ,当且仅当b=0时,它是实
数;当且仅当a=b=0时,它是实数0;当b≠0时,
叫作虚数;当a=0且b≠0叫作纯虚数.
复数的概念
课文精讲
例如,3+4i是复数,实部是3,虚部是4;
虚数-0.5i的实部是0,虚部是-0.5;3可以看作
实部是3,虚部是0的复数.
复数的概念
课文精讲
根据复数中a,b 的取值不同,复数可以
有以下的分类:
复数的概念
复数a+bi (a,b∈R)
实数(b=0);
虚数(b≠0).(当a=0时为
纯虚数)
全体复数构成的集合称为复数集,记
作C,显然R C.
∩
≠
课文精讲
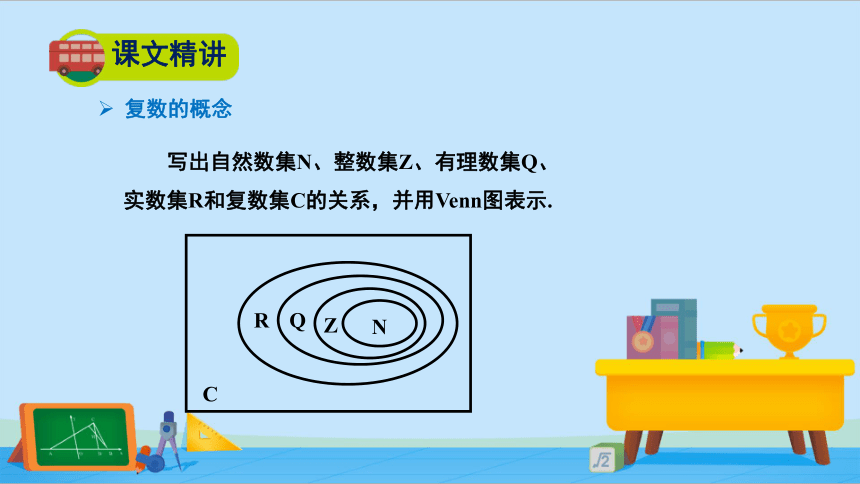
写出自然数集N、整数集Z、有理数集Q、
实数集R和复数集C的关系,并用Venn图表示.
复数的概念
C
R
Q
Z
N
典型例题
例1:说出下列三个复数的实部、虚部,并指
出它们是实数还是虚数,如果是虚数,请指出
是否为纯虚数:
(1)1-i; (2)?????????i; (3)-7.
?
解: (1)1-i的实部与虚部分别是1和-1,它是
虚数,但不是纯虚数;
典型例题
例1:说出下列三个复数的实部、虚部,并指
出它们是实数还是虚数,如果是虚数,请指出
是否为纯虚数:
(1)1-i; (2)?????????i; (3)-7.
?
解: (2) ?????????i的实部与虚部分别是0和??????????,
它是虚数,而且是纯虚数;
?
典型例题
例1:说出下列三个复数的实部、虚部,并指
出它们是实数还是虚数,如果是虚数,请指出
是否为纯虚数:
(1)1-i; (2)?????????i; (3)-7.
?
解: (3) -7的实部与虚部分别是-7和0,
它是实数.
课文精讲
两个复数a+bi 与c+di (a,b,c , d∈R)相等
定义为:它们的实部相等且虚部相等,即
复数的概念
a+bi= c+di当且仅当a=c且b=d.
应当注意,两个实数可以比较大小,
但是两个复数,如果不全是实数,它们之间
就不能比较大小,只能说相等或不相等.例
如,2+i和3+i之间无大小可言.
典型例题
例2:设x,y∈R,(x+2)-2xi=-3y+(y-1)i,
求x,y的值.
解: 由复数相等的定义,得
x+2=-3y
-2x=y-1
解这个方程组,得
x=1
y=-1
课文精讲
问题提出
我们知道,实数与数轴上的点一一对
应,可以用数轴上的点来表示实数.复数
z=a+bi(a,b∈R)由实部a和虚部b两个实
数确定,复数有什么几何意义呢?
复数的几何意义
课文精讲
分析理解
任何一个复数z=a+bi(a,b∈R),都
可以由一个有序实数对(a,b)唯一确定.
因为有序实数对(a,b)与平面直角坐标系
中的点(a,b)一一对应,所以复数集与平
面直角坐标系中的点集是一一对应的.
复数的几何意义
课文精讲
分析理解
如图,点Z的横坐标是a,纵坐标是b,
复数z=a+bi(a,b∈ R)可以用点Z(a,b)表
示.这个通过建立平面直角坐标系来表示
复数的平面称为复平面,x轴称为实轴,
y轴称为虚轴.
复数的几何意义
Z
b
a
y
x
O
课文精讲
分析理解
显然,实轴的点都表示实数;除了
原点外,虚轴上的点都表示纯虚数.
复数的几何意义
Z
b
a
y
x
O
课文精讲
分析理解
因此,复数z=a+bi与复平面内的点
Z(a,b)是一一对应的,即
复数的几何意义
复数z=a+bi 复平面内的点Z(a,b)
这是复数的一种几何意义.
一一对应
Z
b
a
y
x
O
课文精讲
例如,复平面内的原点(0,0)表示复
数0,实轴上的点(3,0)表示复数3,虚轴
上的(0,-1)表示复数-i,点(-3,2)表示复
数-3+2i等.
复数的几何意义
课文精讲
在平面直角坐标系中,平面向量与有
序实数对一一对应,而有序实数对与复
数也是一一对应的.于是,还可以用平面
向量来表示复数.
复数的几何意义
Z
b
a
y
x
O
课文精讲
如图,复数z=a+bi(a,b∈R)与复
平面内的向量????????=(a,b)也是一一对应
的,即
?
复数的几何意义
复数z=a+bi 平面向量????????
?
一一对应
这是复数的另一种几何意义.
Z
b
a
y
x
O
课文精讲
向量????????的模称为复数的模,记作|z|
或|a+bi|.由向量模的定义可知, |z|= |a+bi|
=?????????+?????????.如果b=0,那么z=a+bi是一个
实数????,它的模等于|z|=?????????+????????? =?????????
=|a| (a的绝对值).
?
复数的几何意义
Z
b
a
y
x
O
课文精讲
虽然两个复数一般不能比较大小,
但它们的模是非负实数,可以比较大小.
复数的几何意义
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (1)复数z的模等于2表明,向量????????的
模等于2,即点Z到原点O的距离等于2,
因此满足条件|z|=2的点Z的集合
是以原点O为圆心,以2为半径
的圆(如图(1)).
?
1
y
x
O
2
|z|=2
图(1)
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2)不等式2≤|z|≤3可以化为不等式组
|z|≤3,
|z|≥2.
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2)满足|z|≤3的点Z的集合是以原点O
为圆心、以3为半径的圆及其内部所有的
点构成的集合;满足|z|≥2的点Z的集合是
以原点O为圆心、以2为半径的圆及其外
部所有的点构成的集合.
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2)因此,满足2≤|z|≤3的点Z的集合是这两个集合的交集,即以原点O为圆心,以2和3为半径的两圆所夹的圆环,并包括圆环的边界.
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2) 如图(2).
3
1
y
x
O
2
2≤|z|≤3
图(2)
课文精讲
若两个复数的实部相等,而虚部互
为相反数,则称这两个复数互为共轭复
数.复数z的共轭复数用????表示·当z=a+bi(a,
b∈R)时, ????=a-bi.显然,在复平面内,表
示两个共扼复数的点关于实轴对称(如图),
并且它们的模相等.
?
Z
b
a
y
x
O
-b
????
?
z
课文精讲
另外,当复数z=a+bi的虚部b=0时,
有z=????.也就是说,任意一个实数的共扼复
数仍是它本身,反之亦然.
?
Z
b
a
y
x
O
-b
????
?
z
课文精讲
例4:在复平面内作出表示下列复数的点,
并分别求出它们的模和共轭复数:
(1) z1=3-2i; (2) z2=?1+????i.
?
解:在复平面内作图如图.
(1) |z1|=|3-2i|=????????+?????????=????????,
????????= 3+2i;
?
·
·
????????=-1-????i
?
z1=3-2i
课文精讲
例4:在复平面内作出表示下列复数的点,
并分别求出它们的模和共轭复数:
(1) z1=3-2i; (2) z2=-1+????i.
?
解:在复平面内作图如图.
(2) |z2|=|-1+????i|=?????????+????????=2,
????????=-1-????i.
?
·
·
????????=-1-????i
?
z1=3-2i
综合练习
若复数z=(m+1)+(2-m)i(m∈R)
是纯虚数,则m=________.
解:复数z=(m+1)+(2-m)i(m∈R)
是纯虚数,
则m+1=0,
解得m=-1.
故答案为:-1.
-1
综合练习
已知z=1-i,则z的共轭复数________.
解:z=1-i,则z的共轭复数:1+i.
故答案为:1+i.
1+i
本课小结
再 见
授课教师:
温故知新
学习目标
1.掌握复数的有关概念,如虚数单位、实部、
虚部、虚数、纯虚数;正确对复数进行分类,
掌握数集之间的从属关系;(重点)
2.理解复平面的实轴、虚轴、复数的模、共轭复
数的概念;(重点)
3.掌握复数的代数表示及其几何意义.(难点)
课文精讲
在数自身的发展中,求解方程是数系扩充
的重要动力.比如,要使像2x=1这样的线性方
程有解,就需要引进有理数;无理数与有理数
构成实数.
然而,即使实数也无法完全满足求解二
次方程的需要. 像x2=?1这样一个简单的方程就
没有实数解,因为任意实数的平方都不可能是
负数.
?
复数的概念
课文精讲
为此,人们开始引进一个新数i,叫作虚
数单位,并规定:
(1)它的平方等于-1,即i2=?1;
(2)实数与它进行四则运算时,原有的加法、
乘法运算律仍然成立.
?
复数的概念
课文精讲
形如a+bi(其中a,b∈R)的数叫作复数,
通常用字母z表示,即z=a+bi (a,b∈R),其
a称为复数z的实部,记作Re z,b称为复数z的
虚部,记作Im z.
对于复数a+bi ,当且仅当b=0时,它是实
数;当且仅当a=b=0时,它是实数0;当b≠0时,
叫作虚数;当a=0且b≠0叫作纯虚数.
复数的概念
课文精讲
例如,3+4i是复数,实部是3,虚部是4;
虚数-0.5i的实部是0,虚部是-0.5;3可以看作
实部是3,虚部是0的复数.
复数的概念
课文精讲
根据复数中a,b 的取值不同,复数可以
有以下的分类:
复数的概念
复数a+bi (a,b∈R)
实数(b=0);
虚数(b≠0).(当a=0时为
纯虚数)
全体复数构成的集合称为复数集,记
作C,显然R C.
∩
≠
课文精讲
写出自然数集N、整数集Z、有理数集Q、
实数集R和复数集C的关系,并用Venn图表示.
复数的概念
C
R
Q
Z
N
典型例题
例1:说出下列三个复数的实部、虚部,并指
出它们是实数还是虚数,如果是虚数,请指出
是否为纯虚数:
(1)1-i; (2)?????????i; (3)-7.
?
解: (1)1-i的实部与虚部分别是1和-1,它是
虚数,但不是纯虚数;
典型例题
例1:说出下列三个复数的实部、虚部,并指
出它们是实数还是虚数,如果是虚数,请指出
是否为纯虚数:
(1)1-i; (2)?????????i; (3)-7.
?
解: (2) ?????????i的实部与虚部分别是0和??????????,
它是虚数,而且是纯虚数;
?
典型例题
例1:说出下列三个复数的实部、虚部,并指
出它们是实数还是虚数,如果是虚数,请指出
是否为纯虚数:
(1)1-i; (2)?????????i; (3)-7.
?
解: (3) -7的实部与虚部分别是-7和0,
它是实数.
课文精讲
两个复数a+bi 与c+di (a,b,c , d∈R)相等
定义为:它们的实部相等且虚部相等,即
复数的概念
a+bi= c+di当且仅当a=c且b=d.
应当注意,两个实数可以比较大小,
但是两个复数,如果不全是实数,它们之间
就不能比较大小,只能说相等或不相等.例
如,2+i和3+i之间无大小可言.
典型例题
例2:设x,y∈R,(x+2)-2xi=-3y+(y-1)i,
求x,y的值.
解: 由复数相等的定义,得
x+2=-3y
-2x=y-1
解这个方程组,得
x=1
y=-1
课文精讲
问题提出
我们知道,实数与数轴上的点一一对
应,可以用数轴上的点来表示实数.复数
z=a+bi(a,b∈R)由实部a和虚部b两个实
数确定,复数有什么几何意义呢?
复数的几何意义
课文精讲
分析理解
任何一个复数z=a+bi(a,b∈R),都
可以由一个有序实数对(a,b)唯一确定.
因为有序实数对(a,b)与平面直角坐标系
中的点(a,b)一一对应,所以复数集与平
面直角坐标系中的点集是一一对应的.
复数的几何意义
课文精讲
分析理解
如图,点Z的横坐标是a,纵坐标是b,
复数z=a+bi(a,b∈ R)可以用点Z(a,b)表
示.这个通过建立平面直角坐标系来表示
复数的平面称为复平面,x轴称为实轴,
y轴称为虚轴.
复数的几何意义
Z
b
a
y
x
O
课文精讲
分析理解
显然,实轴的点都表示实数;除了
原点外,虚轴上的点都表示纯虚数.
复数的几何意义
Z
b
a
y
x
O
课文精讲
分析理解
因此,复数z=a+bi与复平面内的点
Z(a,b)是一一对应的,即
复数的几何意义
复数z=a+bi 复平面内的点Z(a,b)
这是复数的一种几何意义.
一一对应
Z
b
a
y
x
O
课文精讲
例如,复平面内的原点(0,0)表示复
数0,实轴上的点(3,0)表示复数3,虚轴
上的(0,-1)表示复数-i,点(-3,2)表示复
数-3+2i等.
复数的几何意义
课文精讲
在平面直角坐标系中,平面向量与有
序实数对一一对应,而有序实数对与复
数也是一一对应的.于是,还可以用平面
向量来表示复数.
复数的几何意义
Z
b
a
y
x
O
课文精讲
如图,复数z=a+bi(a,b∈R)与复
平面内的向量????????=(a,b)也是一一对应
的,即
?
复数的几何意义
复数z=a+bi 平面向量????????
?
一一对应
这是复数的另一种几何意义.
Z
b
a
y
x
O
课文精讲
向量????????的模称为复数的模,记作|z|
或|a+bi|.由向量模的定义可知, |z|= |a+bi|
=?????????+?????????.如果b=0,那么z=a+bi是一个
实数????,它的模等于|z|=?????????+????????? =?????????
=|a| (a的绝对值).
?
复数的几何意义
Z
b
a
y
x
O
课文精讲
虽然两个复数一般不能比较大小,
但它们的模是非负实数,可以比较大小.
复数的几何意义
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (1)复数z的模等于2表明,向量????????的
模等于2,即点Z到原点O的距离等于2,
因此满足条件|z|=2的点Z的集合
是以原点O为圆心,以2为半径
的圆(如图(1)).
?
1
y
x
O
2
|z|=2
图(1)
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2)不等式2≤|z|≤3可以化为不等式组
|z|≤3,
|z|≥2.
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2)满足|z|≤3的点Z的集合是以原点O
为圆心、以3为半径的圆及其内部所有的
点构成的集合;满足|z|≥2的点Z的集合是
以原点O为圆心、以2为半径的圆及其外
部所有的点构成的集合.
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2)因此,满足2≤|z|≤3的点Z的集合是这两个集合的交集,即以原点O为圆心,以2和3为半径的两圆所夹的圆环,并包括圆环的边界.
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2; (2) 2≤|z|≤3.
解: (2) 如图(2).
3
1
y
x
O
2
2≤|z|≤3
图(2)
课文精讲
若两个复数的实部相等,而虚部互
为相反数,则称这两个复数互为共轭复
数.复数z的共轭复数用????表示·当z=a+bi(a,
b∈R)时, ????=a-bi.显然,在复平面内,表
示两个共扼复数的点关于实轴对称(如图),
并且它们的模相等.
?
Z
b
a
y
x
O
-b
????
?
z
课文精讲
另外,当复数z=a+bi的虚部b=0时,
有z=????.也就是说,任意一个实数的共扼复
数仍是它本身,反之亦然.
?
Z
b
a
y
x
O
-b
????
?
z
课文精讲
例4:在复平面内作出表示下列复数的点,
并分别求出它们的模和共轭复数:
(1) z1=3-2i; (2) z2=?1+????i.
?
解:在复平面内作图如图.
(1) |z1|=|3-2i|=????????+?????????=????????,
????????= 3+2i;
?
·
·
????????=-1-????i
?
z1=3-2i
课文精讲
例4:在复平面内作出表示下列复数的点,
并分别求出它们的模和共轭复数:
(1) z1=3-2i; (2) z2=-1+????i.
?
解:在复平面内作图如图.
(2) |z2|=|-1+????i|=?????????+????????=2,
????????=-1-????i.
?
·
·
????????=-1-????i
?
z1=3-2i
综合练习
若复数z=(m+1)+(2-m)i(m∈R)
是纯虚数,则m=________.
解:复数z=(m+1)+(2-m)i(m∈R)
是纯虚数,
则m+1=0,
解得m=-1.
故答案为:-1.
-1
综合练习
已知z=1-i,则z的共轭复数________.
解:z=1-i,则z的共轭复数:1+i.
故答案为:1+i.
1+i
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
