人教版B版(2019)高中数学必修第四册第十一章立体几何初步11.1.4棱锥与棱台 同步作业(Word含解析)
文档属性
| 名称 | 人教版B版(2019)高中数学必修第四册第十一章立体几何初步11.1.4棱锥与棱台 同步作业(Word含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 158.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 20:28:17 | ||
图片预览




文档简介
棱锥与棱台
1.下面说法中,正确的是
( )
A.上下两个底面平行且是相似四边形的几何体是四棱台
B.棱台的所有侧面都是梯形
C.棱台的侧棱长必相等
D.棱台的上下底面可能不是相似图形
2.设棱锥的底面面积是8
cm2,那么这个棱锥的中截面的面积是
( )
A.4
cm2
B.2
cm2
C.2
cm2
D.
cm2
3.棱长为2的正四面体的高为
( )
A.
B.
C.
D.
4.若一个棱台共有21条棱,则这个棱台是 棱台.?
5.一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为4∶9,则此棱锥的侧棱被分成的上、下两部分之比为 .?
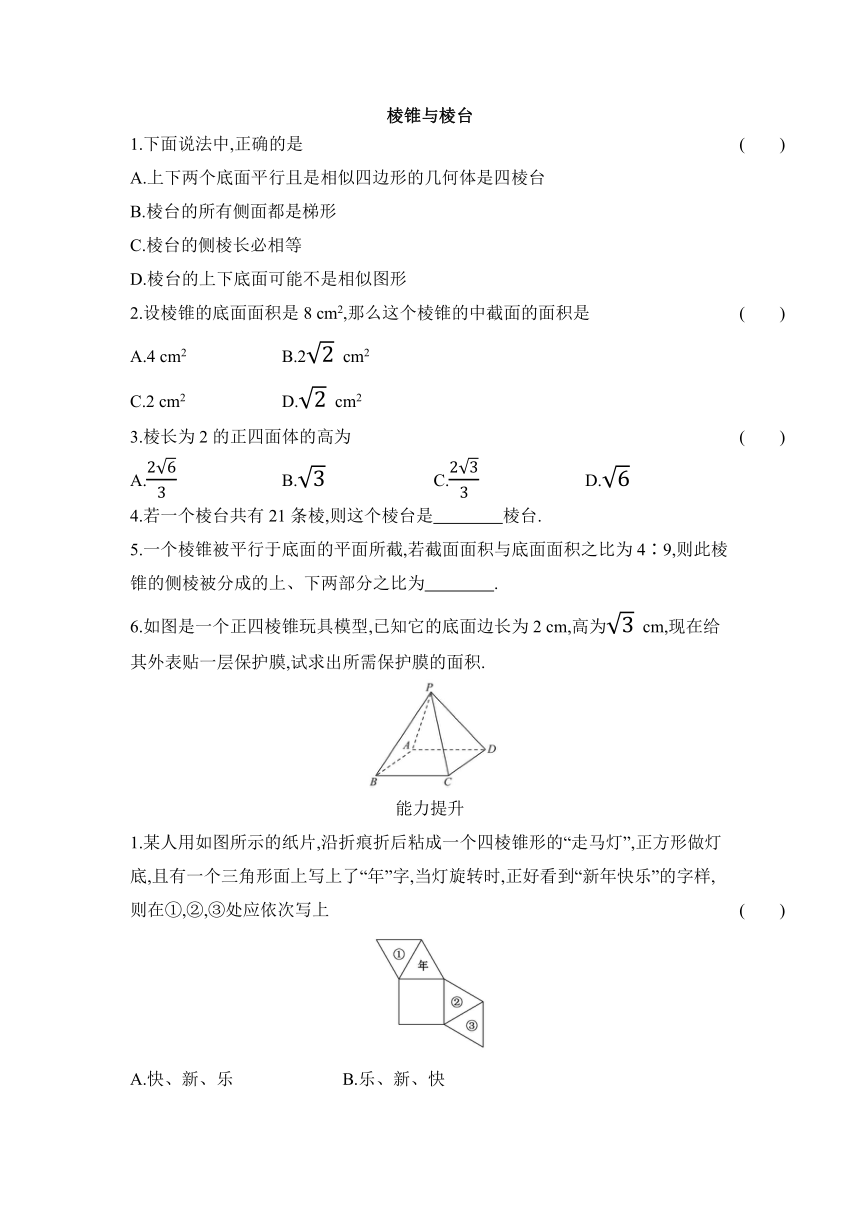
6.如图是一个正四棱锥玩具模型,已知它的底面边长为2
cm,高为
cm,现在给其外表贴一层保护膜,试求出所需保护膜的面积.
能力提升
1.某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①,②,③处应依次写上
( )
A.快、新、乐
B.乐、新、快
C.新、乐、快
D.乐、快、新
2.正方体的8个顶点中,有4个恰为正三棱锥的顶点,则正方体与正三棱锥的表面积之比是
( )
A.
B.
C.
D.
3.用一个平面去截一个三棱锥,截面形状是
( )
A.四边形
B.三角形
C.三角形或四边形
D.不可能为四边形
4.我国古代名著《张丘建算经》中记载:“今有方锥,下广二丈,高三丈.欲斩末为方亭,令上方六尺.问:斩高几何?”大致意思是:有一个正四棱锥下底边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台,且正四棱台的上底边长为六尺,则截去的正四棱锥的高是
( )
A.9尺
B.20尺
C.21尺
D.30尺
5.如果一个棱锥的各条棱长都相等,那么这个棱锥可能是
( )
A.三棱锥
B.四棱锥
C.五棱锥
D.六棱锥
6.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列说法正确的是
( )
A.四面体ABCD每个面的面积相等
B.四面体ABCD每组对棱相互垂直
C.连接四面体ABCD每组对棱中点的线段相互垂直平分
D.从四面体ABCD每个顶点出发的三条棱的长都可以作为一个三角形的三边长
7.正四棱锥S-ABCD的所有棱长都等于a,过不相邻的两条侧棱作截面,则截面的面积为 .?
8.在四棱锥的4个侧面中,直角三角形最多可有 个;在四面体的4个面中,直角三角形最多可有 个.?
9.如果平行于一个正棱锥底面的截面面积是底面面积的,那么截面截一条侧棱所得两条线段的比是多少?
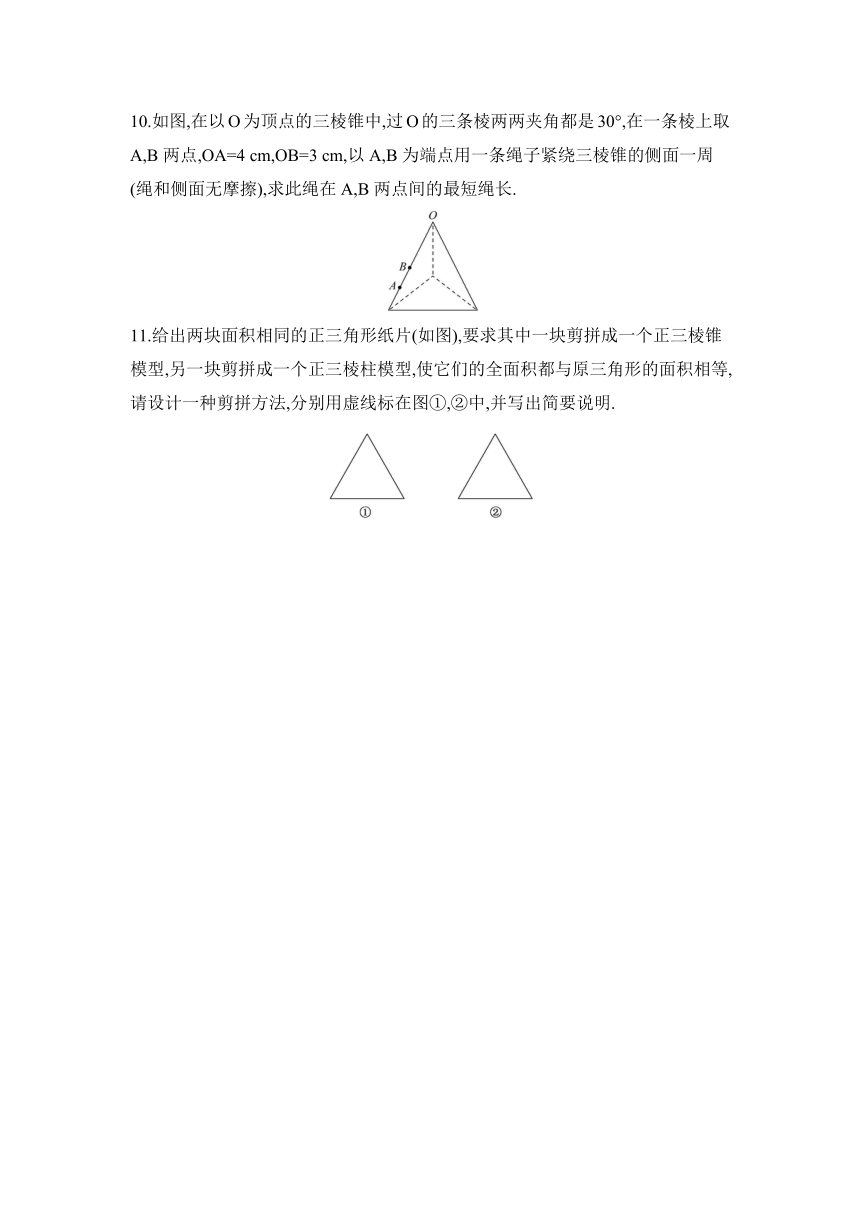
10.如图,在以O为顶点的三棱锥中,过O的三条棱两两夹角都是30°,在一条棱上取A,B两点,OA=4
cm,OB=3
cm,以A,B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A,B两点间的最短绳长.
11.给出两块面积相同的正三角形纸片(如图),要求其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标在图①,②中,并写出简要说明.
答案
1.下面说法中,正确的是
( )
A.上下两个底面平行且是相似四边形的几何体是四棱台
B.棱台的所有侧面都是梯形
C.棱台的侧棱长必相等
D.棱台的上下底面可能不是相似图形
分析:选B.由棱台的结构特点可知,A、C、D不正确.
2.设棱锥的底面面积是8
cm2,那么这个棱锥的中截面的面积是
( )
A.4
cm2
B.2
cm2
C.2
cm2
D.
cm2
分析:选C.根据棱锥的几何特征可知:棱锥的中截面与棱锥的底面是相似的,且相似比等于,所以棱锥的中截面面积与棱锥的底面面积之比为,
所以中截面面积为8×=2(cm2).
3.棱长为2的正四面体的高为
( )
A.
B.
C.
D.
分析:选A.如图,正四面体ABCD,AO是底面BCD上的高,O是△BCD的中心,
则O在中线BM上,且BO=BM=××2=,AO===.
4.若一个棱台共有21条棱,则这个棱台是 棱台.?
分析:设底面边数为x,由棱台的概念可知,棱台的上下底面为相似多边形,边数相同;底面的棱有2x.侧面为梯形,侧面个数与底面多边形边数相同,侧棱为x,棱数共有3x,即3x=21,x=7,所以该棱台为七棱台.
答案:七
5.一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为4∶9,则此棱锥的侧棱被分成的上、下两部分之比为 .?
分析:设棱锥为S-ABCD,截面为A′B′C′D′,
则=,所以==.
所以=.
答案:2∶1
6.如图是一个正四棱锥玩具模型,已知它的底面边长为2
cm,高为
cm,现在给其外表贴一层保护膜,试求出所需保护膜的面积.
分析:如图,连接BD,取BD中点为O,CD中点为E,连接OP,OE,PE,
则OE∥BC,且OE=BC;
因为正四棱锥P-ABCD底面边长为2
cm,高为
cm,
所以OP=
cm,OE=1
cm,
所以PE==2
cm,
又PC=PD,所以PE⊥CD,
因此S△PCD=CD·PE=×2×2=2(cm2),底面正方形的面积为S1=2×2=4(cm2),所以给该正四棱锥玩具模型外表贴一层保护膜,所需保护膜的面积为S=4S△PCD+S1=4×2+4=12(cm2).
能力提升
1.某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①,②,③处应依次写上
( )
A.快、新、乐
B.乐、新、快
C.新、乐、快
D.乐、快、新
分析:选A.根据四棱锥图形,正好看到“新年快乐”的字样,可知顺序为②年①③.
2.正方体的8个顶点中,有4个恰为正三棱锥的顶点,则正方体与正三棱锥的表面积之比是
( )
A.
B.
C.
D.
分析:选B.不妨设正三棱锥的顶点为A,C,B1,D1,
设正方体的棱长为1,则正三棱锥的棱长为.
所以正方体的表面积为6,正三棱锥的表面积为2.
所以它们的表面积之比为.
3.用一个平面去截一个三棱锥,截面形状是
( )
A.四边形
B.三角形
C.三角形或四边形
D.不可能为四边形
分析:选C.当截面图形如图所示时,依次为三角形与四边形.
4.我国古代名著《张丘建算经》中记载:“今有方锥,下广二丈,高三丈.欲斩末为方亭,令上方六尺.问:斩高几何?”大致意思是:有一个正四棱锥下底边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台,且正四棱台的上底边长为六尺,则截去的正四棱锥的高是
( )
A.9尺
B.20尺
C.21尺
D.30尺
分析:选A.如图所示,正四棱锥P-ABCD的下底边长为二丈,即AB=20尺,高三丈,即PO=30尺;截去一段后,得正四棱台ABCD-A′B′C′D′,且上底边长为A′B′=6尺,所以=,解得OO′=21,所以该正四棱台的高是21尺,截去的正四棱锥的高是9尺.
5.如果一个棱锥的各条棱长都相等,那么这个棱锥可能是
( )
A.三棱锥
B.四棱锥
C.五棱锥
D.六棱锥
分析:选ABC.由题意可知,每个侧面均为等边三角形,因为每个侧面的顶角为60°,故三棱锥、四棱锥、五棱锥都有可能.若是六棱锥,因为6×60°=360°,所以顶点会在底面上,因此这个棱锥一定不是六棱锥.
6.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列说法正确的是
( )
A.四面体ABCD每个面的面积相等
B.四面体ABCD每组对棱相互垂直
C.连接四面体ABCD每组对棱中点的线段相互垂直平分
D.从四面体ABCD每个顶点出发的三条棱的长都可以作为一个三角形的三边长
分析:选ACD.由题意可知四面体ABCD为长方体的面对角线组成的三棱锥,如图所示;
由四面体的对棱相等可知四面体的各个面全等,它们的面积相等,则A正确;当四面体棱长都相等时,四面体的每组对棱互相垂直,则B错误;
由长方体的性质可知四面体的对棱中点连线必经过长方体的中心,由对称性知连接四面体ABCD每组对棱中点的线段相互垂直平分,则C正确;
由AC=BD,AB=CD,AD=BC,可得从四面体任意顶点出发的三条棱的长都等于△ABD的三边长,则D正确.
7.正四棱锥S-ABCD的所有棱长都等于a,过不相邻的两条侧棱作截面,则截面的面积为 .?
分析:取AC的中点O,连接SO,则SO⊥AC,如图所示.
因为正四棱锥S-ABCD的所有棱长都等于a,
所以AC=a,SO==a,则截面△SAC的面积为×a×a=a2.
答案:a2
8.在四棱锥的4个侧面中,直角三角形最多可有 个;在四面体的4个面中,直角三角形最多可有 个.?
分析:画出正方体ABCD-EFGH如图所示,
根据正方体的几何性质可知,在四棱锥H-ABCD中,△HAD,△HAB,△HBC,△HCD都是直角三角形,共4个.在四面体H-ABD中,△HAD,△HAB,△HBD,△ABD都是直角三角形,共4个.
答案:4 4
9.如果平行于一个正棱锥底面的截面面积是底面面积的,那么截面截一条侧棱所得两条线段的比是多少?
分析:如图,因为=,所以=,
所以=,
即截面截一条侧棱所得两条线段的比为1∶(-1).
10.如图,在以O为顶点的三棱锥中,过O的三条棱两两夹角都是30°,在一条棱上取A,B两点,OA=4
cm,OB=3
cm,以A,B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A,B两点间的最短绳长.
分析:作出三棱锥的侧面展开图,如图A,B两点间最短绳长就是线段AB的长度.
在△AOB中,∠AOB=30°×3=90°,
OA=4
cm,OB=3
cm,
所以AB==5
cm.
所以此绳在A,B两点间的最短绳长为5
cm.
11.给出两块面积相同的正三角形纸片(如图),要求其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标在图①,②中,并写出简要说明.
分析:紧扣正三棱锥、正三棱柱的定义.正三棱柱底面是正三角形,侧棱垂直于底面且侧面是全等的矩形,在要求全面积的前提下构造上底面三角形和面积相等的三个四边形.
如图③,沿正三角形三边中点连线折起,即可拼成一个正三棱锥.
如图④,在正三角形三个角上剪出三个相同的四边形,其较长的一组邻边长为三角形边长的,有一组对角为直角,余下的部分沿虚线折起,可成为一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好可以拼成这个正三棱柱的上底.
1.下面说法中,正确的是
( )
A.上下两个底面平行且是相似四边形的几何体是四棱台
B.棱台的所有侧面都是梯形
C.棱台的侧棱长必相等
D.棱台的上下底面可能不是相似图形
2.设棱锥的底面面积是8
cm2,那么这个棱锥的中截面的面积是
( )
A.4
cm2
B.2
cm2
C.2
cm2
D.
cm2
3.棱长为2的正四面体的高为
( )
A.
B.
C.
D.
4.若一个棱台共有21条棱,则这个棱台是 棱台.?
5.一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为4∶9,则此棱锥的侧棱被分成的上、下两部分之比为 .?
6.如图是一个正四棱锥玩具模型,已知它的底面边长为2
cm,高为
cm,现在给其外表贴一层保护膜,试求出所需保护膜的面积.
能力提升
1.某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①,②,③处应依次写上
( )
A.快、新、乐
B.乐、新、快
C.新、乐、快
D.乐、快、新
2.正方体的8个顶点中,有4个恰为正三棱锥的顶点,则正方体与正三棱锥的表面积之比是
( )
A.
B.
C.
D.
3.用一个平面去截一个三棱锥,截面形状是
( )
A.四边形
B.三角形
C.三角形或四边形
D.不可能为四边形
4.我国古代名著《张丘建算经》中记载:“今有方锥,下广二丈,高三丈.欲斩末为方亭,令上方六尺.问:斩高几何?”大致意思是:有一个正四棱锥下底边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台,且正四棱台的上底边长为六尺,则截去的正四棱锥的高是
( )
A.9尺
B.20尺
C.21尺
D.30尺
5.如果一个棱锥的各条棱长都相等,那么这个棱锥可能是
( )
A.三棱锥
B.四棱锥
C.五棱锥
D.六棱锥
6.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列说法正确的是
( )
A.四面体ABCD每个面的面积相等
B.四面体ABCD每组对棱相互垂直
C.连接四面体ABCD每组对棱中点的线段相互垂直平分
D.从四面体ABCD每个顶点出发的三条棱的长都可以作为一个三角形的三边长
7.正四棱锥S-ABCD的所有棱长都等于a,过不相邻的两条侧棱作截面,则截面的面积为 .?
8.在四棱锥的4个侧面中,直角三角形最多可有 个;在四面体的4个面中,直角三角形最多可有 个.?
9.如果平行于一个正棱锥底面的截面面积是底面面积的,那么截面截一条侧棱所得两条线段的比是多少?
10.如图,在以O为顶点的三棱锥中,过O的三条棱两两夹角都是30°,在一条棱上取A,B两点,OA=4
cm,OB=3
cm,以A,B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A,B两点间的最短绳长.
11.给出两块面积相同的正三角形纸片(如图),要求其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标在图①,②中,并写出简要说明.
答案
1.下面说法中,正确的是
( )
A.上下两个底面平行且是相似四边形的几何体是四棱台
B.棱台的所有侧面都是梯形
C.棱台的侧棱长必相等
D.棱台的上下底面可能不是相似图形
分析:选B.由棱台的结构特点可知,A、C、D不正确.
2.设棱锥的底面面积是8
cm2,那么这个棱锥的中截面的面积是
( )
A.4
cm2
B.2
cm2
C.2
cm2
D.
cm2
分析:选C.根据棱锥的几何特征可知:棱锥的中截面与棱锥的底面是相似的,且相似比等于,所以棱锥的中截面面积与棱锥的底面面积之比为,
所以中截面面积为8×=2(cm2).
3.棱长为2的正四面体的高为
( )
A.
B.
C.
D.
分析:选A.如图,正四面体ABCD,AO是底面BCD上的高,O是△BCD的中心,
则O在中线BM上,且BO=BM=××2=,AO===.
4.若一个棱台共有21条棱,则这个棱台是 棱台.?
分析:设底面边数为x,由棱台的概念可知,棱台的上下底面为相似多边形,边数相同;底面的棱有2x.侧面为梯形,侧面个数与底面多边形边数相同,侧棱为x,棱数共有3x,即3x=21,x=7,所以该棱台为七棱台.
答案:七
5.一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为4∶9,则此棱锥的侧棱被分成的上、下两部分之比为 .?
分析:设棱锥为S-ABCD,截面为A′B′C′D′,
则=,所以==.
所以=.
答案:2∶1
6.如图是一个正四棱锥玩具模型,已知它的底面边长为2
cm,高为
cm,现在给其外表贴一层保护膜,试求出所需保护膜的面积.
分析:如图,连接BD,取BD中点为O,CD中点为E,连接OP,OE,PE,
则OE∥BC,且OE=BC;
因为正四棱锥P-ABCD底面边长为2
cm,高为
cm,
所以OP=
cm,OE=1
cm,
所以PE==2
cm,
又PC=PD,所以PE⊥CD,
因此S△PCD=CD·PE=×2×2=2(cm2),底面正方形的面积为S1=2×2=4(cm2),所以给该正四棱锥玩具模型外表贴一层保护膜,所需保护膜的面积为S=4S△PCD+S1=4×2+4=12(cm2).
能力提升
1.某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①,②,③处应依次写上
( )
A.快、新、乐
B.乐、新、快
C.新、乐、快
D.乐、快、新
分析:选A.根据四棱锥图形,正好看到“新年快乐”的字样,可知顺序为②年①③.
2.正方体的8个顶点中,有4个恰为正三棱锥的顶点,则正方体与正三棱锥的表面积之比是
( )
A.
B.
C.
D.
分析:选B.不妨设正三棱锥的顶点为A,C,B1,D1,
设正方体的棱长为1,则正三棱锥的棱长为.
所以正方体的表面积为6,正三棱锥的表面积为2.
所以它们的表面积之比为.
3.用一个平面去截一个三棱锥,截面形状是
( )
A.四边形
B.三角形
C.三角形或四边形
D.不可能为四边形
分析:选C.当截面图形如图所示时,依次为三角形与四边形.
4.我国古代名著《张丘建算经》中记载:“今有方锥,下广二丈,高三丈.欲斩末为方亭,令上方六尺.问:斩高几何?”大致意思是:有一个正四棱锥下底边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台,且正四棱台的上底边长为六尺,则截去的正四棱锥的高是
( )
A.9尺
B.20尺
C.21尺
D.30尺
分析:选A.如图所示,正四棱锥P-ABCD的下底边长为二丈,即AB=20尺,高三丈,即PO=30尺;截去一段后,得正四棱台ABCD-A′B′C′D′,且上底边长为A′B′=6尺,所以=,解得OO′=21,所以该正四棱台的高是21尺,截去的正四棱锥的高是9尺.
5.如果一个棱锥的各条棱长都相等,那么这个棱锥可能是
( )
A.三棱锥
B.四棱锥
C.五棱锥
D.六棱锥
分析:选ABC.由题意可知,每个侧面均为等边三角形,因为每个侧面的顶角为60°,故三棱锥、四棱锥、五棱锥都有可能.若是六棱锥,因为6×60°=360°,所以顶点会在底面上,因此这个棱锥一定不是六棱锥.
6.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列说法正确的是
( )
A.四面体ABCD每个面的面积相等
B.四面体ABCD每组对棱相互垂直
C.连接四面体ABCD每组对棱中点的线段相互垂直平分
D.从四面体ABCD每个顶点出发的三条棱的长都可以作为一个三角形的三边长
分析:选ACD.由题意可知四面体ABCD为长方体的面对角线组成的三棱锥,如图所示;
由四面体的对棱相等可知四面体的各个面全等,它们的面积相等,则A正确;当四面体棱长都相等时,四面体的每组对棱互相垂直,则B错误;
由长方体的性质可知四面体的对棱中点连线必经过长方体的中心,由对称性知连接四面体ABCD每组对棱中点的线段相互垂直平分,则C正确;
由AC=BD,AB=CD,AD=BC,可得从四面体任意顶点出发的三条棱的长都等于△ABD的三边长,则D正确.
7.正四棱锥S-ABCD的所有棱长都等于a,过不相邻的两条侧棱作截面,则截面的面积为 .?
分析:取AC的中点O,连接SO,则SO⊥AC,如图所示.
因为正四棱锥S-ABCD的所有棱长都等于a,
所以AC=a,SO==a,则截面△SAC的面积为×a×a=a2.
答案:a2
8.在四棱锥的4个侧面中,直角三角形最多可有 个;在四面体的4个面中,直角三角形最多可有 个.?
分析:画出正方体ABCD-EFGH如图所示,
根据正方体的几何性质可知,在四棱锥H-ABCD中,△HAD,△HAB,△HBC,△HCD都是直角三角形,共4个.在四面体H-ABD中,△HAD,△HAB,△HBD,△ABD都是直角三角形,共4个.
答案:4 4
9.如果平行于一个正棱锥底面的截面面积是底面面积的,那么截面截一条侧棱所得两条线段的比是多少?
分析:如图,因为=,所以=,
所以=,
即截面截一条侧棱所得两条线段的比为1∶(-1).
10.如图,在以O为顶点的三棱锥中,过O的三条棱两两夹角都是30°,在一条棱上取A,B两点,OA=4
cm,OB=3
cm,以A,B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A,B两点间的最短绳长.
分析:作出三棱锥的侧面展开图,如图A,B两点间最短绳长就是线段AB的长度.
在△AOB中,∠AOB=30°×3=90°,
OA=4
cm,OB=3
cm,
所以AB==5
cm.
所以此绳在A,B两点间的最短绳长为5
cm.
11.给出两块面积相同的正三角形纸片(如图),要求其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标在图①,②中,并写出简要说明.
分析:紧扣正三棱锥、正三棱柱的定义.正三棱柱底面是正三角形,侧棱垂直于底面且侧面是全等的矩形,在要求全面积的前提下构造上底面三角形和面积相等的三个四边形.
如图③,沿正三角形三边中点连线折起,即可拼成一个正三棱锥.
如图④,在正三角形三个角上剪出三个相同的四边形,其较长的一组邻边长为三角形边长的,有一组对角为直角,余下的部分沿虚线折起,可成为一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好可以拼成这个正三棱柱的上底.
