人教版B版(2019)高中数学必修第四册第十一章11.1.5旋转体 课时作业(Word含解析)
文档属性
| 名称 | 人教版B版(2019)高中数学必修第四册第十一章11.1.5旋转体 课时作业(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 255.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 20:28:21 | ||
图片预览




文档简介
11.1.5 旋转体
1.一个等边圆柱(底面直径等于高)的轴截面的面积是2S,则它的一个底面的面积是( )
A.
B.
C.S
D.πS
2.(多选题)下列关于球体的说法正确的是( )
A.球体是空间中到定点的距离等于定长的点的集合
B.球面是空间中到定点的距离等于定长的点的集合
C.一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
3.
在长方形ABCD中挖掉半圆O,得到如图所示的图形,则将该图形绕着AB所在的直线旋转一周后得到的几何体为( )
A.一个长方体内部挖去一个球
B.一个长方体内部挖去半个球
C.一个圆柱体内部挖去一个球
D.一个圆柱体内部挖去半个球
4设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2
B.6πa2
C.12πa2
D.24πa2
5.用长为4、宽为2的矩形做侧面围成一个高为2的圆柱,此圆柱的轴截面面积为( )
A.8
B.
C.
D.
6.我国古代数学名著《数学九章》中有云:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺”(注:1丈等于10尺)( )
A.29尺
B.24尺
C.26尺
D.30尺
7.下列说法正确的是 .(填序号)?
①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;
②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台;
③圆柱、圆锥、圆台都有两个底面;
④圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的母线长.
8.
图中平面图形从下往上依次由等腰梯形、矩形、半圆、圆、等腰三角形拼接形成,若将它绕直线l旋转形成一个组合体,下面说法不正确的是 (填序号).?
①该组合体可以分割成圆台、圆柱、圆锥和两个球;
②该组合体中的圆锥和球只有一个公共点;
③该组合体中的球和半球只有一个公共点.
9.一个圆锥的轴截面为边长为a的正三角形,则其表面积为 .?
10.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,求球O的半径.
11.
如图所示,已知圆柱的高为80
cm,底面半径为10
cm,表面上有P,Q两点,若P,Q两点在轴截面ABB1A1上,且PA=40
cm,B1Q=30
cm,一只蚂蚁沿着侧面从P点爬到Q点,求蚂蚁爬行的最短路程.
素养提升
1.如果圆锥的侧面展开图是半圆,那么这个圆锥的轴截面对应的等腰三角形的底角是( )
A.30°
B.45°
C.60°
D.90°
2.一个四面体各棱长都为,四个顶点在同一球面上,则此球的表面积为( )
A.3π
B.4π
C.3π
D.6π
3.已知一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A.
B.
C.
D.
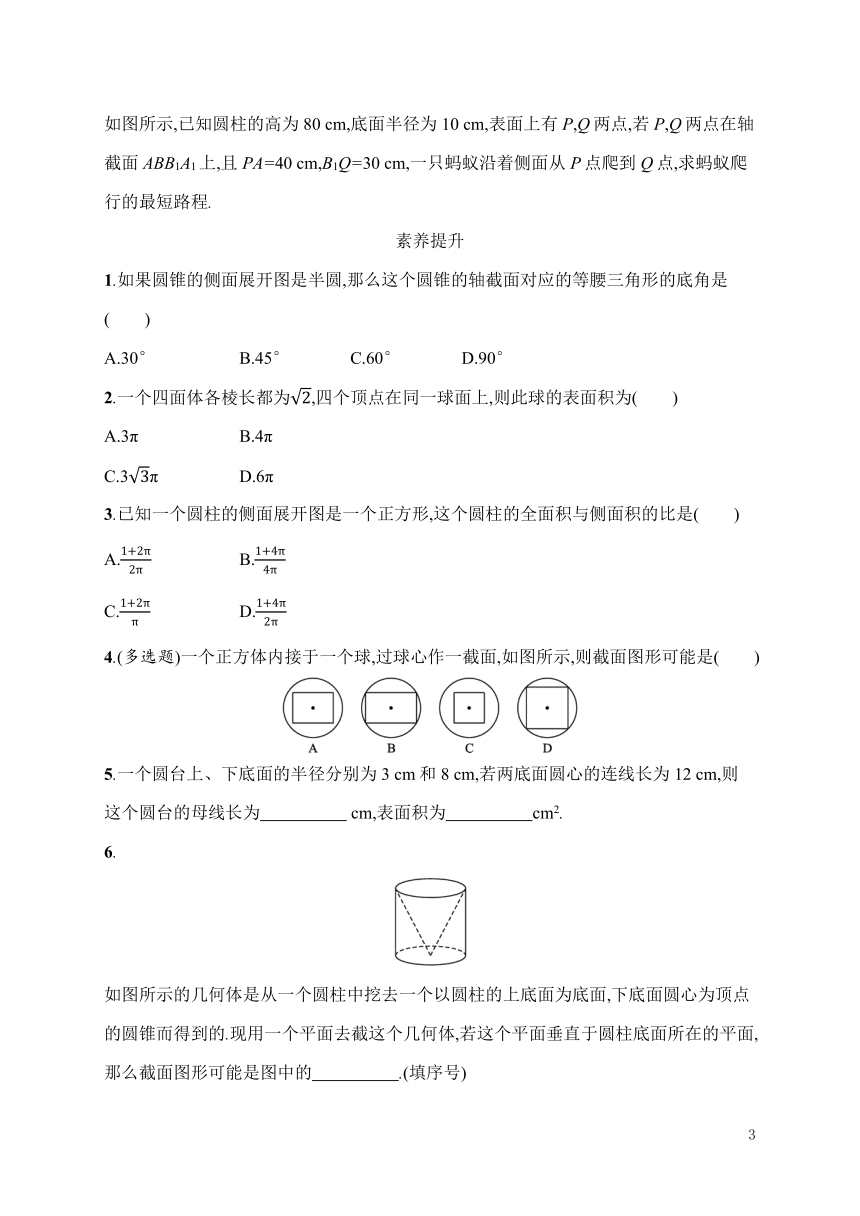
4.(多选题)一个正方体内接于一个球,过球心作一截面,如图所示,则截面图形可能是( )
5.一个圆台上、下底面的半径分别为3
cm和8
cm,若两底面圆心的连线长为12
cm,则这个圆台的母线长为
cm,表面积为 cm2.?
6.
如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面垂直于圆柱底面所在的平面,那么截面图形可能是图中的 .(填序号)?
7.定义如图所示的几何体为斜截圆柱(由不平行圆柱底面的平面截圆柱得到),已知斜截圆柱底面的直径为40
cm,母线长最短为50
cm、最长为80
cm,则斜截圆柱侧面展开图的面积S=
cm2.?
8.已知球的两个平行截面的面积分别为5π和8π,且两截面位于球心的同侧,且距离等于1,求这个球的半径.
9.
如图,已知在直角三角形ABC中,AC⊥BC,BC=2,tan
∠ABC=2.
(1)若以直线AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.
(2)一只蚂蚁在问题(1)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.
答案
1.一个等边圆柱(底面直径等于高)的轴截面的面积是2S,则它的一个底面的面积是( )
A.
B.
C.S
D.πS
答案A
解析设底面半径为r,则4r2=2S,故底面面积=πr2=π·.故选A.
2.(多选题)下列关于球体的说法正确的是( )
A.球体是空间中到定点的距离等于定长的点的集合
B.球面是空间中到定点的距离等于定长的点的集合
C.一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
答案BC
解析空间中到定点的距离等于定长的点的集合是球面,所以A错误,B正确;由球体的定义,知C正确;
球的每一条直径所在的直线均为它的对称轴,所以D错误.
3.
在长方形ABCD中挖掉半圆O,得到如图所示的图形,则将该图形绕着AB所在的直线旋转一周后得到的几何体为( )
A.一个长方体内部挖去一个球
B.一个长方体内部挖去半个球
C.一个圆柱体内部挖去一个球
D.一个圆柱体内部挖去半个球
答案C
解析根据空间几何体的结构得知,将该图形绕着AB所在的直线旋转一周后得到的几何体为一个圆柱体内部挖去一个球.故选C.
4设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2
B.6πa2
C.12πa2
D.24πa2
答案B
解析长方体的长,宽,高分别为2a,a,a,其顶点都在一个球面上,长方体的对角线就是外接球的直径,所以球的直径长为a,所以球的半径为a,所以球的表面积是4π=6πa2,故选B.
5.用长为4、宽为2的矩形做侧面围成一个高为2的圆柱,此圆柱的轴截面面积为( )
A.8
B.
C.
D.
答案B
解析易知2πr=4,则2r=,所以轴截面面积=×2=.故选B.
6.我国古代数学名著《数学九章》中有云:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺”(注:1丈等于10尺)( )
A.29尺
B.24尺
C.26尺
D.30尺
答案C
解析由题意,圆柱的侧面展开图是矩形,一条边(即木棍的高)长24尺,另一条边长5×2=10尺,因此葛藤长=26尺,故选C.
7.下列说法正确的是 .(填序号)?
①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;
②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台;
③圆柱、圆锥、圆台都有两个底面;
④圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的母线长.
答案④
解析根据圆柱母线的定义,①错误;以直角梯形垂直于上、下底的腰为轴旋转得到的旋转体是圆台,以另一腰为轴旋转所得的旋转体不是圆台,故②错误;圆锥只有一个底面,故③错误;根据圆锥母线的定义,④正确.
8.
图中平面图形从下往上依次由等腰梯形、矩形、半圆、圆、等腰三角形拼接形成,若将它绕直线l旋转形成一个组合体,下面说法不正确的是 (填序号).?
①该组合体可以分割成圆台、圆柱、圆锥和两个球;
②该组合体中的圆锥和球只有一个公共点;
③该组合体中的球和半球只有一个公共点.
答案①
解析该组合体可以分割成圆锥、球、半球、圆柱、圆台,故①错,②③正确.
9.一个圆锥的轴截面为边长为a的正三角形,则其表面积为 .?
答案πa2
解析由题知,圆锥的底面半径r=,母线长l=a,则其表面积为S表=πr(r+l)=π·πa2.
10.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,求球O的半径.
解如图,设球O的半径为R,则
由AH∶HB=1∶2得HA=·2R=R,
所以OH=.
因为截面面积为π=π·(HM)2,所以HM=1.
在Rt△HMO中,OM2=OH2+HM2,
所以R2=R2+HM2=R2+1,
所以R=,即球O的半径为.
11.
如图所示,已知圆柱的高为80
cm,底面半径为10
cm,表面上有P,Q两点,若P,Q两点在轴截面ABB1A1上,且PA=40
cm,B1Q=30
cm,一只蚂蚁沿着侧面从P点爬到Q点,求蚂蚁爬行的最短路程.
解将
圆柱侧面沿母线AA1展开,得到如图所示的矩形.
设圆柱的底面半径为r,则r=10
cm.
∴A1B1=×2πr=πr=10π(cm).过点Q作QS⊥AA1于点S,在Rt△PQS中,PS=80-40-30=10(cm),QS=A1B1=10π(cm).
∴PQ==10(cm),
即蚂蚁爬过的最短路径长是10
cm.
素养提升
1.如果圆锥的侧面展开图是半圆,那么这个圆锥的轴截面对应的等腰三角形的底角是( )
A.30°
B.45°
C.60°
D.90°
答案C
解析设圆锥的底面半径是r,
母线长是l.如图所示,2πr=πl,
所以2r=l.所以.
所以轴截面对应的等腰三角形的底角为60°.故选C.
2.一个四面体各棱长都为,四个顶点在同一球面上,则此球的表面积为( )
A.3π
B.4π
C.3π
D.6π
答案A
解析把正四面体扩展为正方体,二者有相同的外接球,扩展后正方体的棱长为1,所以正方体对角线的长度就是外接球的直径,所以球的半径为,所以球的表面积为4πR2=4π×=3π,故选A.
3.已知一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A.
B.
C.
D.
答案A
解析设圆柱的底面半径为r,高为h,则由题设知h=2πr,∴S全=2πr2+2πr·h=2πr2(1+2π).又S侧=h2=4π2r2,∴.故选A.
4.(多选题)一个正方体内接于一个球,过球心作一截面,如图所示,则截面图形可能是( )
答案ABC
解析当截面平行于正方体的一个侧面时得C,当截面过正方体的体对角线时得B,当截面不平行于任何侧面也不过对角线时得A,但无论如何都不能截出D.
5.一个圆台上、下底面的半径分别为3
cm和8
cm,若两底面圆心的连线长为12
cm,则这个圆台的母线长为
cm,表面积为 cm2.?
答案13 216π
解析如图,
过点A作AC⊥OB,交OB于点C.在Rt△ABC中,AC=12
cm,BC=8-3=5
cm,所以AB==13(cm).
表面积为S=π(33+82+3×13+8×13)=216π(cm2).
6.
如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面垂直于圆柱底面所在的平面,那么截面图形可能是图中的 .(填序号)?
答案①③
解析在与圆柱底面垂直的截面中,随着截面位置的变化,截面图形也会发生变化.当截面经过圆柱的轴时,所截得的图形是图①.当截面不经过圆柱的轴时,截得的图形是图③.而图②④是不会出现的.
7.定义如图所示的几何体为斜截圆柱(由不平行圆柱底面的平面截圆柱得到),已知斜截圆柱底面的直径为40
cm,母线长最短为50
cm、最长为80
cm,则斜截圆柱侧面展开图的面积S=
cm2.?
答案2
600π
解析把斜截圆柱补成底面半径20
cm,高130
cm的圆柱,则侧面展开可得斜截圆柱侧面展开圆面积S=(50+80)×40π=2
600π(cm2).
8.已知球的两个平行截面的面积分别为5π和8π,且两截面位于球心的同侧,且距离等于1,求这个球的半径.
解如图,
设这两个截面的半径分别为r1,r2,球心到截面的距离分别为d1,d2,球半径为R.则π=5π,π=8π,∴=5,=8.
∵R2=,
∴=8-5=3,
即(d1-d2)(d1+d2)=3.
又d1-d2=1,∴
解得∴R==3.
9.
如图,已知在直角三角形ABC中,AC⊥BC,BC=2,tan
∠ABC=2.
(1)若以直线AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.
(2)一只蚂蚁在问题(1)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.
解(1)在直角三角形ABC中,由BC=2,tan
∠ABC=2,即tan
∠ABC==2,得AC=4.若三角形ABC以直线AC为轴旋转一周,
形成的几何体为以BC=2为半径,高AC=4的圆锥,
则AB==6,其表面积为S=π×22+π×2×6=16π.
(2)由问题(1)的圆锥,要使蚂蚁爬行的距离最短,则沿过点B的母线把圆锥侧面展开为平面图形,如图所示,
所求最短距离就是点B到点B1的距离,∠BAB1=,在△ABB1中,由余弦定理得BB1==6.
3
1.一个等边圆柱(底面直径等于高)的轴截面的面积是2S,则它的一个底面的面积是( )
A.
B.
C.S
D.πS
2.(多选题)下列关于球体的说法正确的是( )
A.球体是空间中到定点的距离等于定长的点的集合
B.球面是空间中到定点的距离等于定长的点的集合
C.一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
3.
在长方形ABCD中挖掉半圆O,得到如图所示的图形,则将该图形绕着AB所在的直线旋转一周后得到的几何体为( )
A.一个长方体内部挖去一个球
B.一个长方体内部挖去半个球
C.一个圆柱体内部挖去一个球
D.一个圆柱体内部挖去半个球
4设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2
B.6πa2
C.12πa2
D.24πa2
5.用长为4、宽为2的矩形做侧面围成一个高为2的圆柱,此圆柱的轴截面面积为( )
A.8
B.
C.
D.
6.我国古代数学名著《数学九章》中有云:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺”(注:1丈等于10尺)( )
A.29尺
B.24尺
C.26尺
D.30尺
7.下列说法正确的是 .(填序号)?
①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;
②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台;
③圆柱、圆锥、圆台都有两个底面;
④圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的母线长.
8.
图中平面图形从下往上依次由等腰梯形、矩形、半圆、圆、等腰三角形拼接形成,若将它绕直线l旋转形成一个组合体,下面说法不正确的是 (填序号).?
①该组合体可以分割成圆台、圆柱、圆锥和两个球;
②该组合体中的圆锥和球只有一个公共点;
③该组合体中的球和半球只有一个公共点.
9.一个圆锥的轴截面为边长为a的正三角形,则其表面积为 .?
10.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,求球O的半径.
11.
如图所示,已知圆柱的高为80
cm,底面半径为10
cm,表面上有P,Q两点,若P,Q两点在轴截面ABB1A1上,且PA=40
cm,B1Q=30
cm,一只蚂蚁沿着侧面从P点爬到Q点,求蚂蚁爬行的最短路程.
素养提升
1.如果圆锥的侧面展开图是半圆,那么这个圆锥的轴截面对应的等腰三角形的底角是( )
A.30°
B.45°
C.60°
D.90°
2.一个四面体各棱长都为,四个顶点在同一球面上,则此球的表面积为( )
A.3π
B.4π
C.3π
D.6π
3.已知一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A.
B.
C.
D.
4.(多选题)一个正方体内接于一个球,过球心作一截面,如图所示,则截面图形可能是( )
5.一个圆台上、下底面的半径分别为3
cm和8
cm,若两底面圆心的连线长为12
cm,则这个圆台的母线长为
cm,表面积为 cm2.?
6.
如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面垂直于圆柱底面所在的平面,那么截面图形可能是图中的 .(填序号)?
7.定义如图所示的几何体为斜截圆柱(由不平行圆柱底面的平面截圆柱得到),已知斜截圆柱底面的直径为40
cm,母线长最短为50
cm、最长为80
cm,则斜截圆柱侧面展开图的面积S=
cm2.?
8.已知球的两个平行截面的面积分别为5π和8π,且两截面位于球心的同侧,且距离等于1,求这个球的半径.
9.
如图,已知在直角三角形ABC中,AC⊥BC,BC=2,tan
∠ABC=2.
(1)若以直线AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.
(2)一只蚂蚁在问题(1)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.
答案
1.一个等边圆柱(底面直径等于高)的轴截面的面积是2S,则它的一个底面的面积是( )
A.
B.
C.S
D.πS
答案A
解析设底面半径为r,则4r2=2S,故底面面积=πr2=π·.故选A.
2.(多选题)下列关于球体的说法正确的是( )
A.球体是空间中到定点的距离等于定长的点的集合
B.球面是空间中到定点的距离等于定长的点的集合
C.一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
答案BC
解析空间中到定点的距离等于定长的点的集合是球面,所以A错误,B正确;由球体的定义,知C正确;
球的每一条直径所在的直线均为它的对称轴,所以D错误.
3.
在长方形ABCD中挖掉半圆O,得到如图所示的图形,则将该图形绕着AB所在的直线旋转一周后得到的几何体为( )
A.一个长方体内部挖去一个球
B.一个长方体内部挖去半个球
C.一个圆柱体内部挖去一个球
D.一个圆柱体内部挖去半个球
答案C
解析根据空间几何体的结构得知,将该图形绕着AB所在的直线旋转一周后得到的几何体为一个圆柱体内部挖去一个球.故选C.
4设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2
B.6πa2
C.12πa2
D.24πa2
答案B
解析长方体的长,宽,高分别为2a,a,a,其顶点都在一个球面上,长方体的对角线就是外接球的直径,所以球的直径长为a,所以球的半径为a,所以球的表面积是4π=6πa2,故选B.
5.用长为4、宽为2的矩形做侧面围成一个高为2的圆柱,此圆柱的轴截面面积为( )
A.8
B.
C.
D.
答案B
解析易知2πr=4,则2r=,所以轴截面面积=×2=.故选B.
6.我国古代数学名著《数学九章》中有云:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺”(注:1丈等于10尺)( )
A.29尺
B.24尺
C.26尺
D.30尺
答案C
解析由题意,圆柱的侧面展开图是矩形,一条边(即木棍的高)长24尺,另一条边长5×2=10尺,因此葛藤长=26尺,故选C.
7.下列说法正确的是 .(填序号)?
①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;
②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台;
③圆柱、圆锥、圆台都有两个底面;
④圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的母线长.
答案④
解析根据圆柱母线的定义,①错误;以直角梯形垂直于上、下底的腰为轴旋转得到的旋转体是圆台,以另一腰为轴旋转所得的旋转体不是圆台,故②错误;圆锥只有一个底面,故③错误;根据圆锥母线的定义,④正确.
8.
图中平面图形从下往上依次由等腰梯形、矩形、半圆、圆、等腰三角形拼接形成,若将它绕直线l旋转形成一个组合体,下面说法不正确的是 (填序号).?
①该组合体可以分割成圆台、圆柱、圆锥和两个球;
②该组合体中的圆锥和球只有一个公共点;
③该组合体中的球和半球只有一个公共点.
答案①
解析该组合体可以分割成圆锥、球、半球、圆柱、圆台,故①错,②③正确.
9.一个圆锥的轴截面为边长为a的正三角形,则其表面积为 .?
答案πa2
解析由题知,圆锥的底面半径r=,母线长l=a,则其表面积为S表=πr(r+l)=π·πa2.
10.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,求球O的半径.
解如图,设球O的半径为R,则
由AH∶HB=1∶2得HA=·2R=R,
所以OH=.
因为截面面积为π=π·(HM)2,所以HM=1.
在Rt△HMO中,OM2=OH2+HM2,
所以R2=R2+HM2=R2+1,
所以R=,即球O的半径为.
11.
如图所示,已知圆柱的高为80
cm,底面半径为10
cm,表面上有P,Q两点,若P,Q两点在轴截面ABB1A1上,且PA=40
cm,B1Q=30
cm,一只蚂蚁沿着侧面从P点爬到Q点,求蚂蚁爬行的最短路程.
解将
圆柱侧面沿母线AA1展开,得到如图所示的矩形.
设圆柱的底面半径为r,则r=10
cm.
∴A1B1=×2πr=πr=10π(cm).过点Q作QS⊥AA1于点S,在Rt△PQS中,PS=80-40-30=10(cm),QS=A1B1=10π(cm).
∴PQ==10(cm),
即蚂蚁爬过的最短路径长是10
cm.
素养提升
1.如果圆锥的侧面展开图是半圆,那么这个圆锥的轴截面对应的等腰三角形的底角是( )
A.30°
B.45°
C.60°
D.90°
答案C
解析设圆锥的底面半径是r,
母线长是l.如图所示,2πr=πl,
所以2r=l.所以.
所以轴截面对应的等腰三角形的底角为60°.故选C.
2.一个四面体各棱长都为,四个顶点在同一球面上,则此球的表面积为( )
A.3π
B.4π
C.3π
D.6π
答案A
解析把正四面体扩展为正方体,二者有相同的外接球,扩展后正方体的棱长为1,所以正方体对角线的长度就是外接球的直径,所以球的半径为,所以球的表面积为4πR2=4π×=3π,故选A.
3.已知一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A.
B.
C.
D.
答案A
解析设圆柱的底面半径为r,高为h,则由题设知h=2πr,∴S全=2πr2+2πr·h=2πr2(1+2π).又S侧=h2=4π2r2,∴.故选A.
4.(多选题)一个正方体内接于一个球,过球心作一截面,如图所示,则截面图形可能是( )
答案ABC
解析当截面平行于正方体的一个侧面时得C,当截面过正方体的体对角线时得B,当截面不平行于任何侧面也不过对角线时得A,但无论如何都不能截出D.
5.一个圆台上、下底面的半径分别为3
cm和8
cm,若两底面圆心的连线长为12
cm,则这个圆台的母线长为
cm,表面积为 cm2.?
答案13 216π
解析如图,
过点A作AC⊥OB,交OB于点C.在Rt△ABC中,AC=12
cm,BC=8-3=5
cm,所以AB==13(cm).
表面积为S=π(33+82+3×13+8×13)=216π(cm2).
6.
如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面垂直于圆柱底面所在的平面,那么截面图形可能是图中的 .(填序号)?
答案①③
解析在与圆柱底面垂直的截面中,随着截面位置的变化,截面图形也会发生变化.当截面经过圆柱的轴时,所截得的图形是图①.当截面不经过圆柱的轴时,截得的图形是图③.而图②④是不会出现的.
7.定义如图所示的几何体为斜截圆柱(由不平行圆柱底面的平面截圆柱得到),已知斜截圆柱底面的直径为40
cm,母线长最短为50
cm、最长为80
cm,则斜截圆柱侧面展开图的面积S=
cm2.?
答案2
600π
解析把斜截圆柱补成底面半径20
cm,高130
cm的圆柱,则侧面展开可得斜截圆柱侧面展开圆面积S=(50+80)×40π=2
600π(cm2).
8.已知球的两个平行截面的面积分别为5π和8π,且两截面位于球心的同侧,且距离等于1,求这个球的半径.
解如图,
设这两个截面的半径分别为r1,r2,球心到截面的距离分别为d1,d2,球半径为R.则π=5π,π=8π,∴=5,=8.
∵R2=,
∴=8-5=3,
即(d1-d2)(d1+d2)=3.
又d1-d2=1,∴
解得∴R==3.
9.
如图,已知在直角三角形ABC中,AC⊥BC,BC=2,tan
∠ABC=2.
(1)若以直线AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.
(2)一只蚂蚁在问题(1)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.
解(1)在直角三角形ABC中,由BC=2,tan
∠ABC=2,即tan
∠ABC==2,得AC=4.若三角形ABC以直线AC为轴旋转一周,
形成的几何体为以BC=2为半径,高AC=4的圆锥,
则AB==6,其表面积为S=π×22+π×2×6=16π.
(2)由问题(1)的圆锥,要使蚂蚁爬行的距离最短,则沿过点B的母线把圆锥侧面展开为平面图形,如图所示,
所求最短距离就是点B到点B1的距离,∠BAB1=,在△ABB1中,由余弦定理得BB1==6.
3
