人教版B版(2019)高中数学必修第四册第十一章11.4.1直线与平面垂直同步作业(Word含解析)
文档属性
| 名称 | 人教版B版(2019)高中数学必修第四册第十一章11.4.1直线与平面垂直同步作业(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览



文档简介
直线与平面垂直
1.下列条件中,能使直线m⊥α的是
( )
A.m⊥b,m⊥c,b?α,c?α
B.m⊥b,b∥α
C.m∩b=A,b⊥α
D.m∥b,b⊥α
2.在正方体ABCD-A1B1C1D1中,E是C1C的中点,则直线BE与平面B1BD所成的角的正弦值为
( )
A.- B. C.- D.
3.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,则下列结论正确的有
( )
①BC⊥平面PAB;②AD⊥PC;③AD⊥平面PBC;④PB⊥平面ADC.
A.0个
B.1个
C.2个
D.3个
4.如图所示,平面α∩β=CD,EA⊥α,垂足为A,EB⊥β,垂足为B,则CD与AB的位置关系是 .?
5.如图,正方体ABCD-A1B1C1D1的棱长为1,过A点作平面A1BD的垂线,垂足为点H,有下列三个结论:
①点H是△A1BD的中心;
②AH垂直于平面CB1D1;
③AC1与B1C所成的角是90°.
其中正确结论的序号是 .?
6.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE.
求证:AB⊥平面ADE.
能力提升
1.如图,设平面α∩平面β=PQ,EG⊥平面α,FH⊥平面α,垂足分别为G,H.为使PQ⊥GH,则需增加的一个条件是( )
A.EF⊥平面α
B.EF⊥平面β
C.PQ⊥GE
D.PQ⊥FH
2.在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是
( )
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段
3.如图,在四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,若直线AB与平面ACD所成角的正弦值为,则点B到平面ACD的距离为
( )
A.
B.
C.
D.
4.如图,在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列结论中正确的有
( )
①总存在某个位置,使CE⊥平面A1DE;
②总有BM∥平面A1DE;
③存在某个位置,使DE⊥A1C.
A.①②
B.①③
C.②③
D.①②③
5.如果一条直线垂直于一个平面内的 ,则能得出直线与平面垂直
( )?
A.三角形的两边
B.梯形的两边
C.圆的两条直径
D.正六边形的两边
6.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
A.AG⊥平面EFH
B.AH⊥平面EFH
C.HF⊥平面AEH
D.HG⊥平面AEF
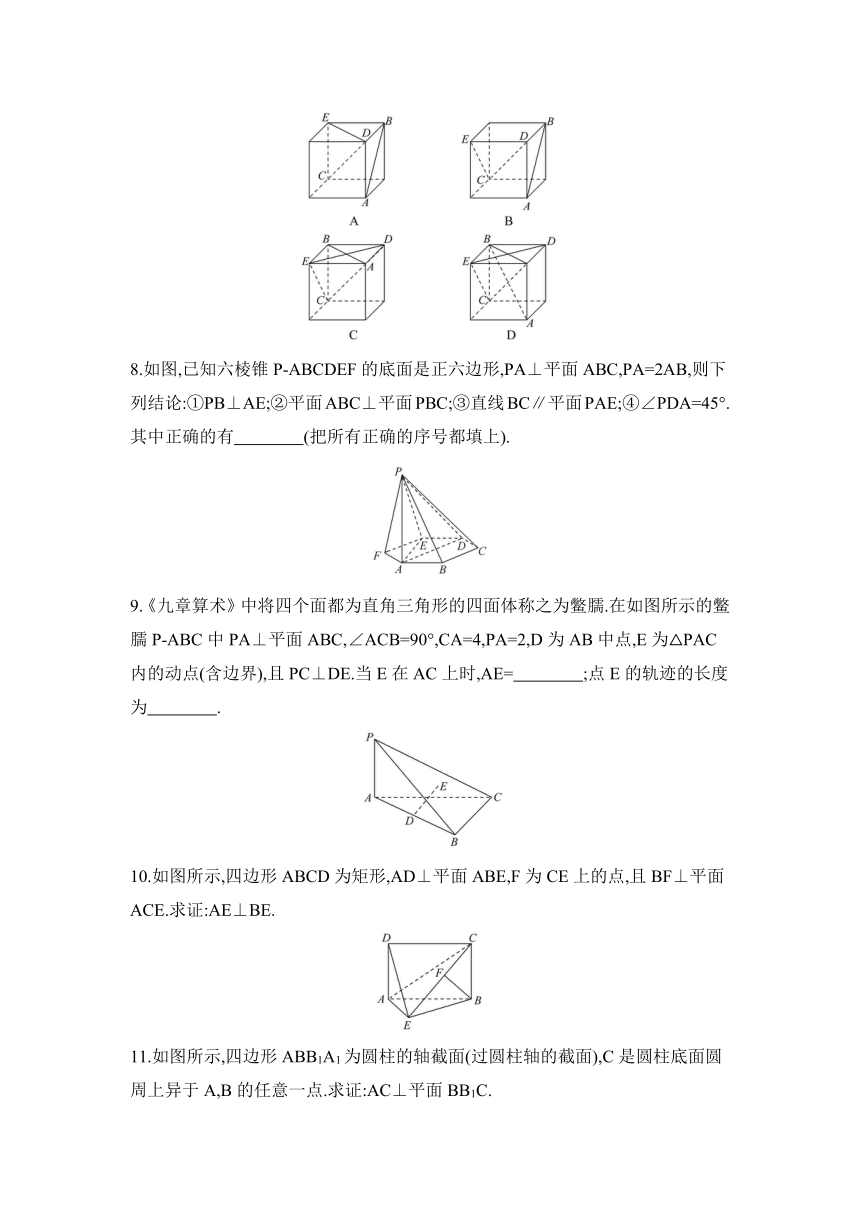
7.(多选题)如图,在以下四个正方体中,直线AB与平面CDE垂直的是
( )
8.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有 (把所有正确的序号都填上).?
9.《九章算术》中将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑P-ABC中PA⊥平面ABC,∠ACB=90°,CA=4,PA=2,D为AB中点,E为△PAC内的动点(含边界),且PC⊥DE.当E在AC上时,AE= ;点E的轨迹的长度为 .?
10.如图所示,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE.求证:AE⊥BE.
11.如图所示,四边形ABB1A1为圆柱的轴截面(过圆柱轴的截面),C是圆柱底面圆周上异于A,B的任意一点.求证:AC⊥平面BB1C.
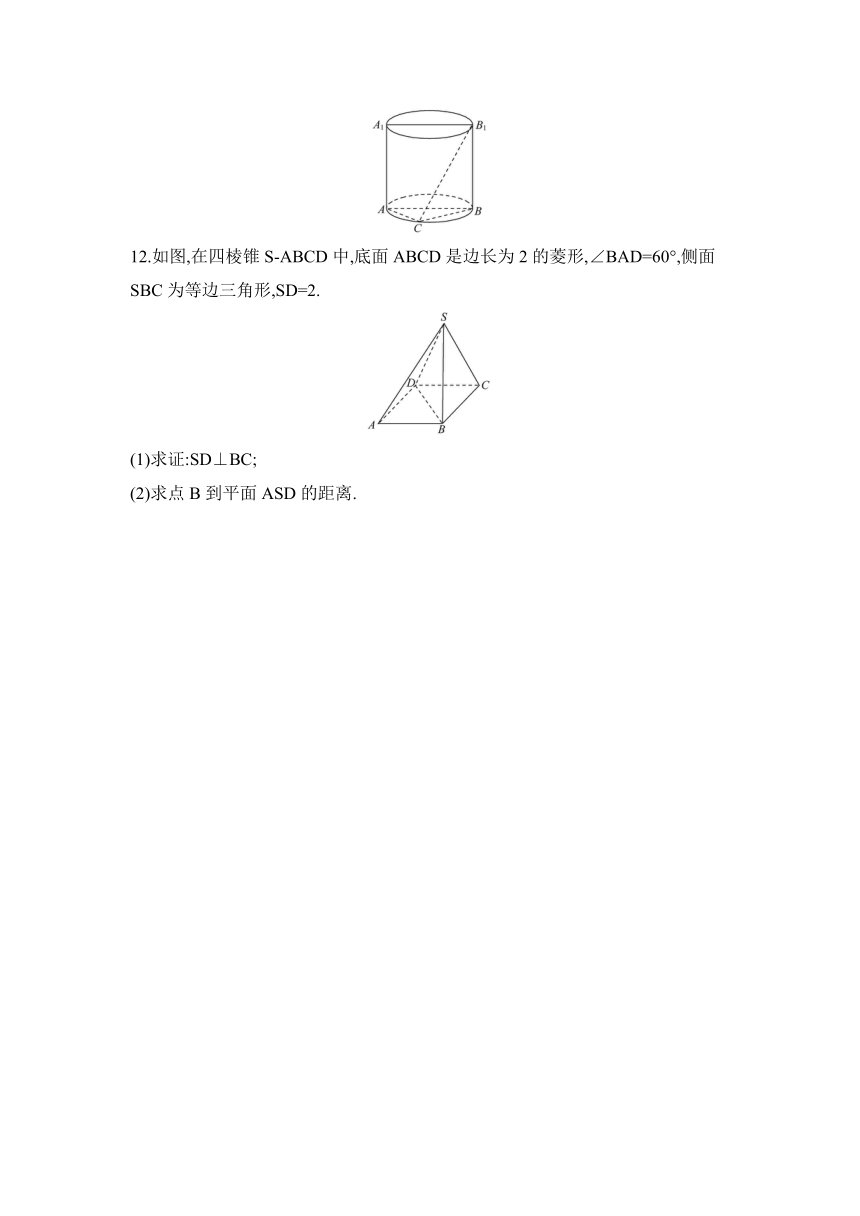
12.如图,在四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧面SBC为等边三角形,SD=2.
(1)求证:SD⊥BC;
(2)求点B到平面ASD的距离.
参考答案
1.下列条件中,能使直线m⊥α的是
( )
A.m⊥b,m⊥c,b?α,c?α
B.m⊥b,b∥α
C.m∩b=A,b⊥α
D.m∥b,b⊥α
分析:选D.对于A,缺b与c相交;对于B,还可能得出m∥α,m与α相交或m?α;对于C,可能有m∥α或m?α或m与α相交.
2.在正方体ABCD-A1B1C1D1中,E是C1C的中点,则直线BE与平面B1BD所成的角的正弦值为
( )
A.- B. C.- D.
分析:选B.取B1D的中点O,连接EO(图略),
则EO∥AC,因为AC⊥平面B1BD,
所以EO⊥平面B1BD,则∠EBO就是直线BE与平面B1BD所成角的平面角,
所以sin∠EBO==.
3.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,则下列结论正确的有
( )
①BC⊥平面PAB;②AD⊥PC;③AD⊥平面PBC;④PB⊥平面ADC.
A.0个
B.1个
C.2个
D.3个
分析:选D.因为PA⊥平面ABC,BC?平面ABC,
则PA⊥BC,又AB⊥BC,PA∩AB=A,故BC⊥平面PAB,①正确;因为BC⊥平面PAB,AD?平面PAB,所以BC⊥AD,因为PA=AB,D为PB的中点,故AD⊥PB,又BC∩PB=B,故AD⊥平面PBC,因为PC?平面PBC,故AD⊥PC,②
③
正确;若PB⊥平面ADC,因为CD?平面ADC,故PB⊥CD,因为D为PB的中点,故CB=CP,又PC>AC>BC,故CB=CP不成立,故④错误.
4.如图所示,平面α∩β=CD,EA⊥α,垂足为A,EB⊥β,垂足为B,则CD与AB的位置关系是 .?
分析:因为EA⊥α,CD?α,
根据直线和平面垂直的定义,则有CD⊥EA.
同理,因为EB⊥β,CD?β,
则有EB⊥CD.又EA∩EB=E,所以CD⊥平面AEB.
又因为AB?平面AEB,所以CD⊥AB.
答案:CD⊥AB
5.如图,正方体ABCD-A1B1C1D1的棱长为1,过A点作平面A1BD的垂线,垂足为点H,有下列三个结论:
①点H是△A1BD的中心;
②AH垂直于平面CB1D1;
③AC1与B1C所成的角是90°.
其中正确结论的序号是 .?
分析:①正确,因为AH⊥平面A1BD,AA1=AB=AD,
所以Rt△AHA1≌Rt△AHD≌Rt△AHB,
所以HA1=HB=HD,
所以点H是△A1BD的外心,又因为A1B=BD=DA1,
所以点H是△A1BD的中心.②正确,易证平面A1BD∥平面CB1D1,
又因为AH⊥平面A1BD,
所以AH垂直于平面CB1D1.③正确,易证A1D⊥平面ABC1D1,所以AC1⊥A1D,又A1D∥B1C,
所以AC1⊥B1C,所以AC1与B1C所成的角是90°.
答案:①②③
6.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE.
求证:AB⊥平面ADE.
【证明】因为AE⊥平面CDE,CD?平面CDE,
所以AE⊥CD,又在正方形ABCD中,CD⊥AD,
AE∩AD=A,所以CD⊥平面ADE,
又在正方形ABCD中,AB∥CD,
所以AB⊥平面ADE.
能力提升
1.如图,设平面α∩平面β=PQ,EG⊥平面α,FH⊥平面α,垂足分别为G,H.为使PQ⊥GH,则需增加的一个条件是( )
A.EF⊥平面α
B.EF⊥平面β
C.PQ⊥GE
D.PQ⊥FH
分析:选B.因为EG⊥平面α,PQ?平面α,所以EG⊥PQ.若EF⊥平面β,则由PQ?平面β,得EF⊥PQ.
又EG与EF为相交直线,所以PQ⊥平面EFHG,
所以PQ⊥GH.
2.在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是
( )
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段
分析:选A.如图,由于BD1⊥平面AB1C,故点P一定位于B1C上.
3.如图,在四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,若直线AB与平面ACD所成角的正弦值为,则点B到平面ACD的距离为
( )
A.
B.
C.
D.
分析:选B.因为AB⊥BC,AB⊥BD,
所以AB⊥平面BCD,故AB⊥CD,
因为CD⊥BE,CD⊥AB,可得CD⊥平面ABE,
则AB在平面ADC上的射影与AE在一条直线上,故直线AB与平面ACD所成角即为∠BAE.
在Rt△ABE中,BE=,sin
∠BAE=,故可得AE=3,AB=4,故VA-BCD=VB-ACD,设点B到平面ACD的距离为x,则S△BCD×AB=S△ACD×x,
整理得2AB=6h,解得h=.
4.如图,在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列结论中正确的有
( )
①总存在某个位置,使CE⊥平面A1DE;
②总有BM∥平面A1DE;
③存在某个位置,使DE⊥A1C.
A.①②
B.①③
C.②③
D.①②③
分析:选A.在①中,总存在某个位置,使CE⊥平面A1DE,①正确;在②中,取CD中点F,连接MF,BF,则MF∥A1D且MF=A1D,FB∥ED且FB=ED,由MF∥A1D与FB∥ED,可得平面MBF∥平面A1DE,所以总有BM∥平面A1DE,故②正确;在③中,A1C在平面ABCD中的射影为AC,AC与DE不垂直,所以DE与A1C不垂直,故③错误.
5.如果一条直线垂直于一个平面内的 ,则能得出直线与平面垂直
( )?
A.三角形的两边
B.梯形的两边
C.圆的两条直径
D.正六边形的两边
分析:选AC.由线面垂直的判定定理知,直线垂直于平面内三角形的两边,因为这两边是相交的,所以能得出直线与平面垂直,所以A选项正确;直线垂直于梯形的两边,因为梯形的两边可能平行,所以不能得出直线与平面垂直,所以B选项不正确;直线垂直于圆的两条直径,因为任何一个圆的两条直径是相交的,所以能得出直线与平面垂直,所以C选项正确;直线垂直于正六边形的两边,因为正六边形的两边可能平行,所以不能得出直线与平面垂直,所以D选项不正确.
6.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
A.AG⊥平面EFH
B.AH⊥平面EFH
C.HF⊥平面AEH
D.HG⊥平面AEF
分析:选BC.由题意可得:AH⊥HE,AH⊥HF.
所以AH⊥平面EFH,而AG与平面EFH不垂直,所以B正确,A不正确.
又HF⊥HE,所以HF⊥平面AHE,C正确.
HG与AG不垂直,因此HG⊥平面AEF不正确,D不正确.
7.(多选题)如图,在以下四个正方体中,直线AB与平面CDE垂直的是
( )
分析:选BD.对于A,由AB与CE所成角为45°,
可得直线AB与平面CDE不垂直;
对于B,由AB⊥CE,AB⊥ED,CE∩ED=E,
可得AB⊥平面CDE;对于C,由AB与CE所成角为60°,可得直线AB与平面CDE不垂直;
对于D,连接AC,由ED⊥平面ABC,
可得ED⊥AB,同理可得EC⊥AB,
又ED∩EC=E,所以AB⊥平面CDE.
8.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有 (把所有正确的序号都填上).?
分析:对于①,因为PA⊥平面ABC,所以PA⊥AE,又EA⊥AB,PA∩AB=A,所以EA⊥平面PAB,从而可得EA⊥PB,故①正确.对于②,由于PA⊥平面ABC,所以平面ABC与平面PBC不可能垂直,故②不正确.对于③,由于在正六边形中BC∥AD,所以BC与EA必有公共点,从而BC与平面PAE有公共点,所以直线BC与平面PAE不平行,故③不正确.对于④,由条件得△PAD为直角三角形,且PA⊥AD,又PA=2AB=AD,所以∠PDA=45°.故④正确.
答案:①④
9.《九章算术》中将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑P-ABC中PA⊥平面ABC,∠ACB=90°,CA=4,PA=2,D为AB中点,E为△PAC内的动点(含边界),且PC⊥DE.当E在AC上时,AE= ;点E的轨迹的长度为 .?
分析:当E在AC上时,
因为PA⊥平面ABC,故PA⊥DE,又PC⊥DE,故DE⊥平面PAC.故DE⊥AC.
又∠ACB=90°,故DE∥BC,D为AB中点,
所以E为AC中点.故AE=AC=2.
取AC中点F,则由(1)有DF⊥平面PAC,故PC⊥DF,又PC⊥DE,
设平面DEF∩PC=G,
则有PC⊥平面DGF.故点E的轨迹为FG.
又此时CF=2,tan∠PCA==,故sin∠PCA==.
所以FG=CF·sin∠PCA==.
答案:2
10.如图所示,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE.求证:AE⊥BE.
【证明】因为AD⊥平面ABE,AD∥BC,
所以BC⊥平面ABE.又AE?平面ABE,
所以AE⊥BC.
因为BF⊥平面ACE,AE?平面ACE,
所以AE⊥BF.
又因为BF?平面BCE,BC?平面BCE,BF∩BC=B,
所以AE⊥平面BCE.
又BE?平面BCE,所以AE⊥BE.
11.如图所示,四边形ABB1A1为圆柱的轴截面(过圆柱轴的截面),C是圆柱底面圆周上异于A,B的任意一点.求证:AC⊥平面BB1C.
【证明】因为四边形ABB1A1为圆柱的轴截面,
所以BB1⊥底面ABC.因为AC?底面ABC,
所以BB1⊥AC.因为AB为底面圆的直径,
所以∠ACB=90°,所以BC⊥AC.
又因为BB1∩BC=B,BB1?平面BB1C,BC?平面BB1C,
所以AC⊥平面BB1C.
12.如图,在四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧面SBC为等边三角形,SD=2.
(1)求证:SD⊥BC;
(2)求点B到平面ASD的距离.
分析:(1)设BC边中点是E,连接DE,SE.
因为△SBC是等边三角形,所以SE⊥BC,
又由已知得△DBC是等边三角形,所以DE⊥BC,
又DE∩SE=E,所以BC⊥平面SDE,所以BC⊥SD.
(2)因为△SBC是边长为2的等边三角形,
所以SE=,同理DE=,又SD=2,
所以S△SDE=×2×=,又由(1)知BC⊥平面SDE,
所以VS-BCD=S△SDE·BC=××2==VS-ABD,
所以VS-ABCD=2VS-BCD=.
又易知三棱锥S-BCD是正四面体,
所以S在底面BCD上的射影H为△BCD各边中线的交点,且为△BCD的重心,
所以H在AC上,由勾股定理,SA=,
又CH=OC=(其中O为AC与BD的交点),
所以SH=,AH=+=,
所以SA=2,
所以SD2+AD2=SA2,所以SD⊥AD,
所以S△SAD=×2×2=2.
设点B到平面ASD的距离为h.
因为VS-ABD=VB-SAD,
所以·S△SAD·h=,所以h=.
故点B到平面ASD的距离为.
1.下列条件中,能使直线m⊥α的是
( )
A.m⊥b,m⊥c,b?α,c?α
B.m⊥b,b∥α
C.m∩b=A,b⊥α
D.m∥b,b⊥α
2.在正方体ABCD-A1B1C1D1中,E是C1C的中点,则直线BE与平面B1BD所成的角的正弦值为
( )
A.- B. C.- D.
3.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,则下列结论正确的有
( )
①BC⊥平面PAB;②AD⊥PC;③AD⊥平面PBC;④PB⊥平面ADC.
A.0个
B.1个
C.2个
D.3个
4.如图所示,平面α∩β=CD,EA⊥α,垂足为A,EB⊥β,垂足为B,则CD与AB的位置关系是 .?
5.如图,正方体ABCD-A1B1C1D1的棱长为1,过A点作平面A1BD的垂线,垂足为点H,有下列三个结论:
①点H是△A1BD的中心;
②AH垂直于平面CB1D1;
③AC1与B1C所成的角是90°.
其中正确结论的序号是 .?
6.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE.
求证:AB⊥平面ADE.
能力提升
1.如图,设平面α∩平面β=PQ,EG⊥平面α,FH⊥平面α,垂足分别为G,H.为使PQ⊥GH,则需增加的一个条件是( )
A.EF⊥平面α
B.EF⊥平面β
C.PQ⊥GE
D.PQ⊥FH
2.在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是
( )
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段
3.如图,在四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,若直线AB与平面ACD所成角的正弦值为,则点B到平面ACD的距离为
( )
A.
B.
C.
D.
4.如图,在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列结论中正确的有
( )
①总存在某个位置,使CE⊥平面A1DE;
②总有BM∥平面A1DE;
③存在某个位置,使DE⊥A1C.
A.①②
B.①③
C.②③
D.①②③
5.如果一条直线垂直于一个平面内的 ,则能得出直线与平面垂直
( )?
A.三角形的两边
B.梯形的两边
C.圆的两条直径
D.正六边形的两边
6.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
A.AG⊥平面EFH
B.AH⊥平面EFH
C.HF⊥平面AEH
D.HG⊥平面AEF
7.(多选题)如图,在以下四个正方体中,直线AB与平面CDE垂直的是
( )
8.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有 (把所有正确的序号都填上).?
9.《九章算术》中将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑P-ABC中PA⊥平面ABC,∠ACB=90°,CA=4,PA=2,D为AB中点,E为△PAC内的动点(含边界),且PC⊥DE.当E在AC上时,AE= ;点E的轨迹的长度为 .?
10.如图所示,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE.求证:AE⊥BE.
11.如图所示,四边形ABB1A1为圆柱的轴截面(过圆柱轴的截面),C是圆柱底面圆周上异于A,B的任意一点.求证:AC⊥平面BB1C.
12.如图,在四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧面SBC为等边三角形,SD=2.
(1)求证:SD⊥BC;
(2)求点B到平面ASD的距离.
参考答案
1.下列条件中,能使直线m⊥α的是
( )
A.m⊥b,m⊥c,b?α,c?α
B.m⊥b,b∥α
C.m∩b=A,b⊥α
D.m∥b,b⊥α
分析:选D.对于A,缺b与c相交;对于B,还可能得出m∥α,m与α相交或m?α;对于C,可能有m∥α或m?α或m与α相交.
2.在正方体ABCD-A1B1C1D1中,E是C1C的中点,则直线BE与平面B1BD所成的角的正弦值为
( )
A.- B. C.- D.
分析:选B.取B1D的中点O,连接EO(图略),
则EO∥AC,因为AC⊥平面B1BD,
所以EO⊥平面B1BD,则∠EBO就是直线BE与平面B1BD所成角的平面角,
所以sin∠EBO==.
3.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,则下列结论正确的有
( )
①BC⊥平面PAB;②AD⊥PC;③AD⊥平面PBC;④PB⊥平面ADC.
A.0个
B.1个
C.2个
D.3个
分析:选D.因为PA⊥平面ABC,BC?平面ABC,
则PA⊥BC,又AB⊥BC,PA∩AB=A,故BC⊥平面PAB,①正确;因为BC⊥平面PAB,AD?平面PAB,所以BC⊥AD,因为PA=AB,D为PB的中点,故AD⊥PB,又BC∩PB=B,故AD⊥平面PBC,因为PC?平面PBC,故AD⊥PC,②
③
正确;若PB⊥平面ADC,因为CD?平面ADC,故PB⊥CD,因为D为PB的中点,故CB=CP,又PC>AC>BC,故CB=CP不成立,故④错误.
4.如图所示,平面α∩β=CD,EA⊥α,垂足为A,EB⊥β,垂足为B,则CD与AB的位置关系是 .?
分析:因为EA⊥α,CD?α,
根据直线和平面垂直的定义,则有CD⊥EA.
同理,因为EB⊥β,CD?β,
则有EB⊥CD.又EA∩EB=E,所以CD⊥平面AEB.
又因为AB?平面AEB,所以CD⊥AB.
答案:CD⊥AB
5.如图,正方体ABCD-A1B1C1D1的棱长为1,过A点作平面A1BD的垂线,垂足为点H,有下列三个结论:
①点H是△A1BD的中心;
②AH垂直于平面CB1D1;
③AC1与B1C所成的角是90°.
其中正确结论的序号是 .?
分析:①正确,因为AH⊥平面A1BD,AA1=AB=AD,
所以Rt△AHA1≌Rt△AHD≌Rt△AHB,
所以HA1=HB=HD,
所以点H是△A1BD的外心,又因为A1B=BD=DA1,
所以点H是△A1BD的中心.②正确,易证平面A1BD∥平面CB1D1,
又因为AH⊥平面A1BD,
所以AH垂直于平面CB1D1.③正确,易证A1D⊥平面ABC1D1,所以AC1⊥A1D,又A1D∥B1C,
所以AC1⊥B1C,所以AC1与B1C所成的角是90°.
答案:①②③
6.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE.
求证:AB⊥平面ADE.
【证明】因为AE⊥平面CDE,CD?平面CDE,
所以AE⊥CD,又在正方形ABCD中,CD⊥AD,
AE∩AD=A,所以CD⊥平面ADE,
又在正方形ABCD中,AB∥CD,
所以AB⊥平面ADE.
能力提升
1.如图,设平面α∩平面β=PQ,EG⊥平面α,FH⊥平面α,垂足分别为G,H.为使PQ⊥GH,则需增加的一个条件是( )
A.EF⊥平面α
B.EF⊥平面β
C.PQ⊥GE
D.PQ⊥FH
分析:选B.因为EG⊥平面α,PQ?平面α,所以EG⊥PQ.若EF⊥平面β,则由PQ?平面β,得EF⊥PQ.
又EG与EF为相交直线,所以PQ⊥平面EFHG,
所以PQ⊥GH.
2.在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是
( )
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段
分析:选A.如图,由于BD1⊥平面AB1C,故点P一定位于B1C上.
3.如图,在四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,若直线AB与平面ACD所成角的正弦值为,则点B到平面ACD的距离为
( )
A.
B.
C.
D.
分析:选B.因为AB⊥BC,AB⊥BD,
所以AB⊥平面BCD,故AB⊥CD,
因为CD⊥BE,CD⊥AB,可得CD⊥平面ABE,
则AB在平面ADC上的射影与AE在一条直线上,故直线AB与平面ACD所成角即为∠BAE.
在Rt△ABE中,BE=,sin
∠BAE=,故可得AE=3,AB=4,故VA-BCD=VB-ACD,设点B到平面ACD的距离为x,则S△BCD×AB=S△ACD×x,
整理得2AB=6h,解得h=.
4.如图,在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列结论中正确的有
( )
①总存在某个位置,使CE⊥平面A1DE;
②总有BM∥平面A1DE;
③存在某个位置,使DE⊥A1C.
A.①②
B.①③
C.②③
D.①②③
分析:选A.在①中,总存在某个位置,使CE⊥平面A1DE,①正确;在②中,取CD中点F,连接MF,BF,则MF∥A1D且MF=A1D,FB∥ED且FB=ED,由MF∥A1D与FB∥ED,可得平面MBF∥平面A1DE,所以总有BM∥平面A1DE,故②正确;在③中,A1C在平面ABCD中的射影为AC,AC与DE不垂直,所以DE与A1C不垂直,故③错误.
5.如果一条直线垂直于一个平面内的 ,则能得出直线与平面垂直
( )?
A.三角形的两边
B.梯形的两边
C.圆的两条直径
D.正六边形的两边
分析:选AC.由线面垂直的判定定理知,直线垂直于平面内三角形的两边,因为这两边是相交的,所以能得出直线与平面垂直,所以A选项正确;直线垂直于梯形的两边,因为梯形的两边可能平行,所以不能得出直线与平面垂直,所以B选项不正确;直线垂直于圆的两条直径,因为任何一个圆的两条直径是相交的,所以能得出直线与平面垂直,所以C选项正确;直线垂直于正六边形的两边,因为正六边形的两边可能平行,所以不能得出直线与平面垂直,所以D选项不正确.
6.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
A.AG⊥平面EFH
B.AH⊥平面EFH
C.HF⊥平面AEH
D.HG⊥平面AEF
分析:选BC.由题意可得:AH⊥HE,AH⊥HF.
所以AH⊥平面EFH,而AG与平面EFH不垂直,所以B正确,A不正确.
又HF⊥HE,所以HF⊥平面AHE,C正确.
HG与AG不垂直,因此HG⊥平面AEF不正确,D不正确.
7.(多选题)如图,在以下四个正方体中,直线AB与平面CDE垂直的是
( )
分析:选BD.对于A,由AB与CE所成角为45°,
可得直线AB与平面CDE不垂直;
对于B,由AB⊥CE,AB⊥ED,CE∩ED=E,
可得AB⊥平面CDE;对于C,由AB与CE所成角为60°,可得直线AB与平面CDE不垂直;
对于D,连接AC,由ED⊥平面ABC,
可得ED⊥AB,同理可得EC⊥AB,
又ED∩EC=E,所以AB⊥平面CDE.
8.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有 (把所有正确的序号都填上).?
分析:对于①,因为PA⊥平面ABC,所以PA⊥AE,又EA⊥AB,PA∩AB=A,所以EA⊥平面PAB,从而可得EA⊥PB,故①正确.对于②,由于PA⊥平面ABC,所以平面ABC与平面PBC不可能垂直,故②不正确.对于③,由于在正六边形中BC∥AD,所以BC与EA必有公共点,从而BC与平面PAE有公共点,所以直线BC与平面PAE不平行,故③不正确.对于④,由条件得△PAD为直角三角形,且PA⊥AD,又PA=2AB=AD,所以∠PDA=45°.故④正确.
答案:①④
9.《九章算术》中将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑P-ABC中PA⊥平面ABC,∠ACB=90°,CA=4,PA=2,D为AB中点,E为△PAC内的动点(含边界),且PC⊥DE.当E在AC上时,AE= ;点E的轨迹的长度为 .?
分析:当E在AC上时,
因为PA⊥平面ABC,故PA⊥DE,又PC⊥DE,故DE⊥平面PAC.故DE⊥AC.
又∠ACB=90°,故DE∥BC,D为AB中点,
所以E为AC中点.故AE=AC=2.
取AC中点F,则由(1)有DF⊥平面PAC,故PC⊥DF,又PC⊥DE,
设平面DEF∩PC=G,
则有PC⊥平面DGF.故点E的轨迹为FG.
又此时CF=2,tan∠PCA==,故sin∠PCA==.
所以FG=CF·sin∠PCA==.
答案:2
10.如图所示,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE.求证:AE⊥BE.
【证明】因为AD⊥平面ABE,AD∥BC,
所以BC⊥平面ABE.又AE?平面ABE,
所以AE⊥BC.
因为BF⊥平面ACE,AE?平面ACE,
所以AE⊥BF.
又因为BF?平面BCE,BC?平面BCE,BF∩BC=B,
所以AE⊥平面BCE.
又BE?平面BCE,所以AE⊥BE.
11.如图所示,四边形ABB1A1为圆柱的轴截面(过圆柱轴的截面),C是圆柱底面圆周上异于A,B的任意一点.求证:AC⊥平面BB1C.
【证明】因为四边形ABB1A1为圆柱的轴截面,
所以BB1⊥底面ABC.因为AC?底面ABC,
所以BB1⊥AC.因为AB为底面圆的直径,
所以∠ACB=90°,所以BC⊥AC.
又因为BB1∩BC=B,BB1?平面BB1C,BC?平面BB1C,
所以AC⊥平面BB1C.
12.如图,在四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧面SBC为等边三角形,SD=2.
(1)求证:SD⊥BC;
(2)求点B到平面ASD的距离.
分析:(1)设BC边中点是E,连接DE,SE.
因为△SBC是等边三角形,所以SE⊥BC,
又由已知得△DBC是等边三角形,所以DE⊥BC,
又DE∩SE=E,所以BC⊥平面SDE,所以BC⊥SD.
(2)因为△SBC是边长为2的等边三角形,
所以SE=,同理DE=,又SD=2,
所以S△SDE=×2×=,又由(1)知BC⊥平面SDE,
所以VS-BCD=S△SDE·BC=××2==VS-ABD,
所以VS-ABCD=2VS-BCD=.
又易知三棱锥S-BCD是正四面体,
所以S在底面BCD上的射影H为△BCD各边中线的交点,且为△BCD的重心,
所以H在AC上,由勾股定理,SA=,
又CH=OC=(其中O为AC与BD的交点),
所以SH=,AH=+=,
所以SA=2,
所以SD2+AD2=SA2,所以SD⊥AD,
所以S△SAD=×2×2=2.
设点B到平面ASD的距离为h.
因为VS-ABD=VB-SAD,
所以·S△SAD·h=,所以h=.
故点B到平面ASD的距离为.
