同底数幂的乘法
图片预览











文档简介
(共31张PPT)
在物理学和天文学中,常用光年作为衡量两个星球之间的距离。1光年是指光在真空中穿行1年的距离.如果光在真空中的速度约是3×105km/s,1年以3.2×107s来计算的话,那么1光年等于多少km?(请列出计算式)
问题引入
如105 ×107 =
提出问题
那么怎么去求幂与幂之间的乘积呢
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
3、a · a · · · · · · a = a( )
n个
3
5
n
①什么叫乘方
②乘方的结果叫做什么
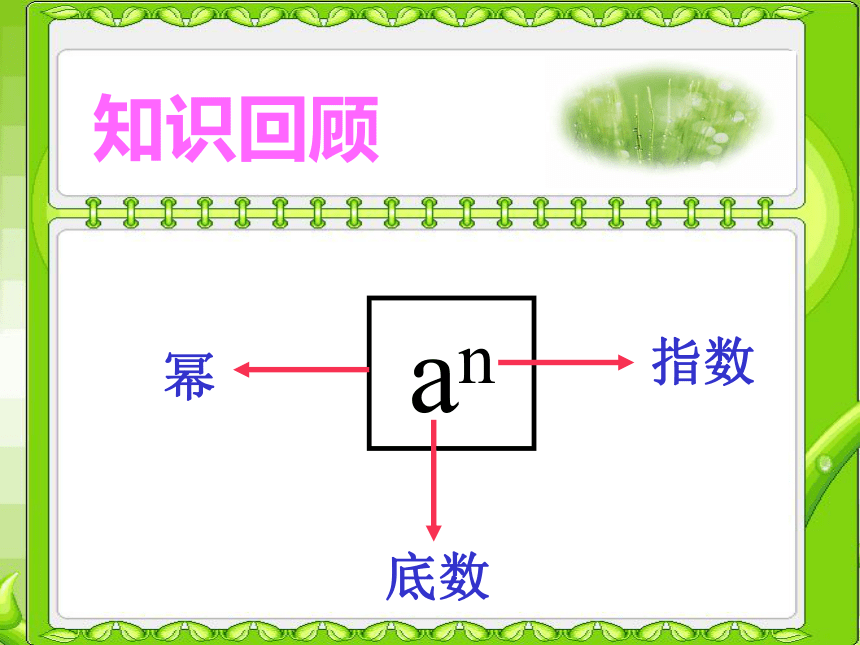
知识回顾
an
底数
指数
幂
知识回顾
请你说出下列各幂的底数和指数:
知识回顾
说出am的乘方意义,并将下列各式写成乘法形式:
(1) 108
(2) (-2)4
=10×10×10×10×10×10×10×10
=(-2)×(-2)×(-2)×(-2)
自主学习 —思考
(1) 22×23=_____(乘方的意义) =_____(乘法结合律)=____ (乘方的意义)
(2) 53×54=_____(乘方的意义) =_____(乘法结合律)=____ (乘方的意义)
(3) a2 · a5 =_____(乘方的意义) =_____(乘法结合律)=____ (乘方的意义)
试一试:
=25 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=57
(1) 22 ×23
(2) 53×54
=(2 ×2) ×(2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 (乘法结合律)
=a7 (乘方的意义)
继续探索:
(3) a2 · a5
=(a · a) (a · a · a · a · a) (乘方的意义)
= a · a · a · a · a · a · a (乘法结合律)
这几道题有什么共同的特点呢 计算的结果有什么规律吗
(1)22 ×23
=a7
=25
(2)53×54
=57
(3)a2 · a5
=(a · a) (a · a · a · a · a)
=(2 ×2) ×(2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
(1)22 ×23
=a7
=25
(2)53×54
=57
(3)a2 · a5
=(a · a) (a · a · a · a · a)
=(2 ×2) ×(2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
=22+3
=53+4
=a2+5
根据上面的规律,请以幂的形式直接写出下列各题的结果:
106
109
10m+n
m+n
如果把(3)中指数3、4换成正整数m、n,你能得出am · an的结果吗?
(4)am · an =
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
知识推导
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 43×45=
43+5
=48
运算形式
运算方法
(同底、乘法)
(底不变、指相加)
幂的底数必须相同,
相乘时指数才能相加.
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
例1:计算
(3) a · a3 · a5 = a4 · a5 =a9
(1) 105×107 (2) a · a3 (3)a · a3 · a5
解:(1) 105×107 =105+7 =1012
(2) a · a3 = a 1+3=a4
am · an = am+n
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
a · a3 · a5 = a4 · a5 =a9
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
am · an = am+n
1.计算:
(1)(-8)7 ×(-8)4 ;
(2)x2 · x5
(1)23×24×25 (2)y · y2 · y3
解:(1)23×24×25=23+4+5=212
(2)y · y2 · y3 = y1+2+3=y6
2.计算:
牛刀小试
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n
辨一辨
① a · a2= a2
② a+a2 = a3
③ a3 · a3= a9
④ a3+a3 = a6
(×)
(×)
(×)
判断下列计算是否正确,并简要说明理由:
(×)
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n
深入探索----想一想(1)
① 32×3m =
② 5m· 5n =
③ x3 · xn+1 =
④y · yn+2 · yn+4 =
3m+2
5m+n
y2n+7
Xn+4
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n
深入探索----想一想(2)
计 算:(结果写成幂的形式)
① (- 2)4× 25 =
②( -x ) 3 ×x 2 =
③ (a-b)2 · (b-a)5 =
29
(b-a)7
公式中的a可代表一个数、字母、式子等.
-x5
八年级 数学
第十四章 整式的乘法
14.1.1同底数幂的乘法
am · an = am+n
深入探索----算一算
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
计算:(结果写成幂的形式)
转 化
的思想
方 法
填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
八年级 数学
第十四章 整式的乘法
14.1.1同底数幂的乘法
am · an = am+n
已知:am=2, an=3.
求am+n =?.
解: am+n = am · an
=2 × 3=6
深入探索----议一议
(1)填空
检测提高
(1)x5 ·( )= x 8
(2)a ·( )= a6
(3)x · x3( )= x7
(4)xm ·( )=x3m
(5)x5·x( )=x3·x7=x( ) ·x6=x·x( )
(6)an+1·a( )=a2n+1=a·a( )
x 3
a 5
x 2m
5
4
9
n
2n
x 3
检测提高
(2) 计算
① (x+y)3·(x+y)4
② xn·xn+1+x2n·x (n是正整数)
③ b2·bm-2+b·bm-1-b3·bm-5·b2
小结:
今天,我们学到了什么?
同底数幂的乘法:
am · an = am+n (m、n为正整数)
同底数幂相乘,底数不变,指数相加。
am · an · ap = am+n+p
( m、n、p为正整数)
祝大家马到成功!
在物理学和天文学中,常用光年作为衡量两个星球之间的距离。1光年是指光在真空中穿行1年的距离.如果光在真空中的速度约是3×105km/s,1年以3.2×107s来计算的话,那么1光年等于多少km?(请列出计算式)
问题引入
如105 ×107 =
提出问题
那么怎么去求幂与幂之间的乘积呢
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
3、a · a · · · · · · a = a( )
n个
3
5
n
①什么叫乘方
②乘方的结果叫做什么
知识回顾
an
底数
指数
幂
知识回顾
请你说出下列各幂的底数和指数:
知识回顾
说出am的乘方意义,并将下列各式写成乘法形式:
(1) 108
(2) (-2)4
=10×10×10×10×10×10×10×10
=(-2)×(-2)×(-2)×(-2)
自主学习 —思考
(1) 22×23=_____(乘方的意义) =_____(乘法结合律)=____ (乘方的意义)
(2) 53×54=_____(乘方的意义) =_____(乘法结合律)=____ (乘方的意义)
(3) a2 · a5 =_____(乘方的意义) =_____(乘法结合律)=____ (乘方的意义)
试一试:
=25 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=57
(1) 22 ×23
(2) 53×54
=(2 ×2) ×(2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 (乘法结合律)
=a7 (乘方的意义)
继续探索:
(3) a2 · a5
=(a · a) (a · a · a · a · a) (乘方的意义)
= a · a · a · a · a · a · a (乘法结合律)
这几道题有什么共同的特点呢 计算的结果有什么规律吗
(1)22 ×23
=a7
=25
(2)53×54
=57
(3)a2 · a5
=(a · a) (a · a · a · a · a)
=(2 ×2) ×(2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
(1)22 ×23
=a7
=25
(2)53×54
=57
(3)a2 · a5
=(a · a) (a · a · a · a · a)
=(2 ×2) ×(2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
=22+3
=53+4
=a2+5
根据上面的规律,请以幂的形式直接写出下列各题的结果:
106
109
10m+n
m+n
如果把(3)中指数3、4换成正整数m、n,你能得出am · an的结果吗?
(4)am · an =
(1)23 ×24
=a7
=27
(2)53×54
=57
(3)a3 · a4
=(a · a · a) (a · a · a · a)
=(2 ×2 ×2) ×(2 ×2 ×2 ×2)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
知识推导
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 43×45=
43+5
=48
运算形式
运算方法
(同底、乘法)
(底不变、指相加)
幂的底数必须相同,
相乘时指数才能相加.
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
例1:计算
(3) a · a3 · a5 = a4 · a5 =a9
(1) 105×107 (2) a · a3 (3)a · a3 · a5
解:(1) 105×107 =105+7 =1012
(2) a · a3 = a 1+3=a4
am · an = am+n
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
a · a3 · a5 = a4 · a5 =a9
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
am · an = am+n
1.计算:
(1)(-8)7 ×(-8)4 ;
(2)x2 · x5
(1)23×24×25 (2)y · y2 · y3
解:(1)23×24×25=23+4+5=212
(2)y · y2 · y3 = y1+2+3=y6
2.计算:
牛刀小试
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n
辨一辨
① a · a2= a2
② a+a2 = a3
③ a3 · a3= a9
④ a3+a3 = a6
(×)
(×)
(×)
判断下列计算是否正确,并简要说明理由:
(×)
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n
深入探索----想一想(1)
① 32×3m =
② 5m· 5n =
③ x3 · xn+1 =
④y · yn+2 · yn+4 =
3m+2
5m+n
y2n+7
Xn+4
八年级 数学
第十五章 整式的乘法
15.1.1同底数幂的乘法
am · an = am+n
深入探索----想一想(2)
计 算:(结果写成幂的形式)
① (- 2)4× 25 =
②( -x ) 3 ×x 2 =
③ (a-b)2 · (b-a)5 =
29
(b-a)7
公式中的a可代表一个数、字母、式子等.
-x5
八年级 数学
第十四章 整式的乘法
14.1.1同底数幂的乘法
am · an = am+n
深入探索----算一算
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
计算:(结果写成幂的形式)
转 化
的思想
方 法
填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
八年级 数学
第十四章 整式的乘法
14.1.1同底数幂的乘法
am · an = am+n
已知:am=2, an=3.
求am+n =?.
解: am+n = am · an
=2 × 3=6
深入探索----议一议
(1)填空
检测提高
(1)x5 ·( )= x 8
(2)a ·( )= a6
(3)x · x3( )= x7
(4)xm ·( )=x3m
(5)x5·x( )=x3·x7=x( ) ·x6=x·x( )
(6)an+1·a( )=a2n+1=a·a( )
x 3
a 5
x 2m
5
4
9
n
2n
x 3
检测提高
(2) 计算
① (x+y)3·(x+y)4
② xn·xn+1+x2n·x (n是正整数)
③ b2·bm-2+b·bm-1-b3·bm-5·b2
小结:
今天,我们学到了什么?
同底数幂的乘法:
am · an = am+n (m、n为正整数)
同底数幂相乘,底数不变,指数相加。
am · an · ap = am+n+p
( m、n、p为正整数)
祝大家马到成功!
