7.1条件概率与全概率公式-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案)
文档属性
| 名称 | 7.1条件概率与全概率公式-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 244.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览


文档简介
690245-167640第七章随机变量及其分布
第七章随机变量及其分布
1150620711207.1条件概率与全概率公式
7.1条件概率与全概率公式
134620183515 知识点1-----条件概率
知识点1-----条件概率
1.定义:
条件概率揭示了P(A),P(AB),P()三者之间“知二求一”的关系
一般地,设A,B为两个随机事件,且P(A)>0,我们称P()=为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
2. 条件概率的定义
设A、B是两个事件,且P(B)>0,则称
false
为在事件B发生的条件下,事件A的条件概率.若事件B已发生, 则为使 A也发生 , 试验结果必须是既在 B 中又在A中的样本点 , 即此点必属于AB. 由于我们已经知道B已发生, 故B变成了新的样本空间 , 于是有了以上公式
条件概率的计算
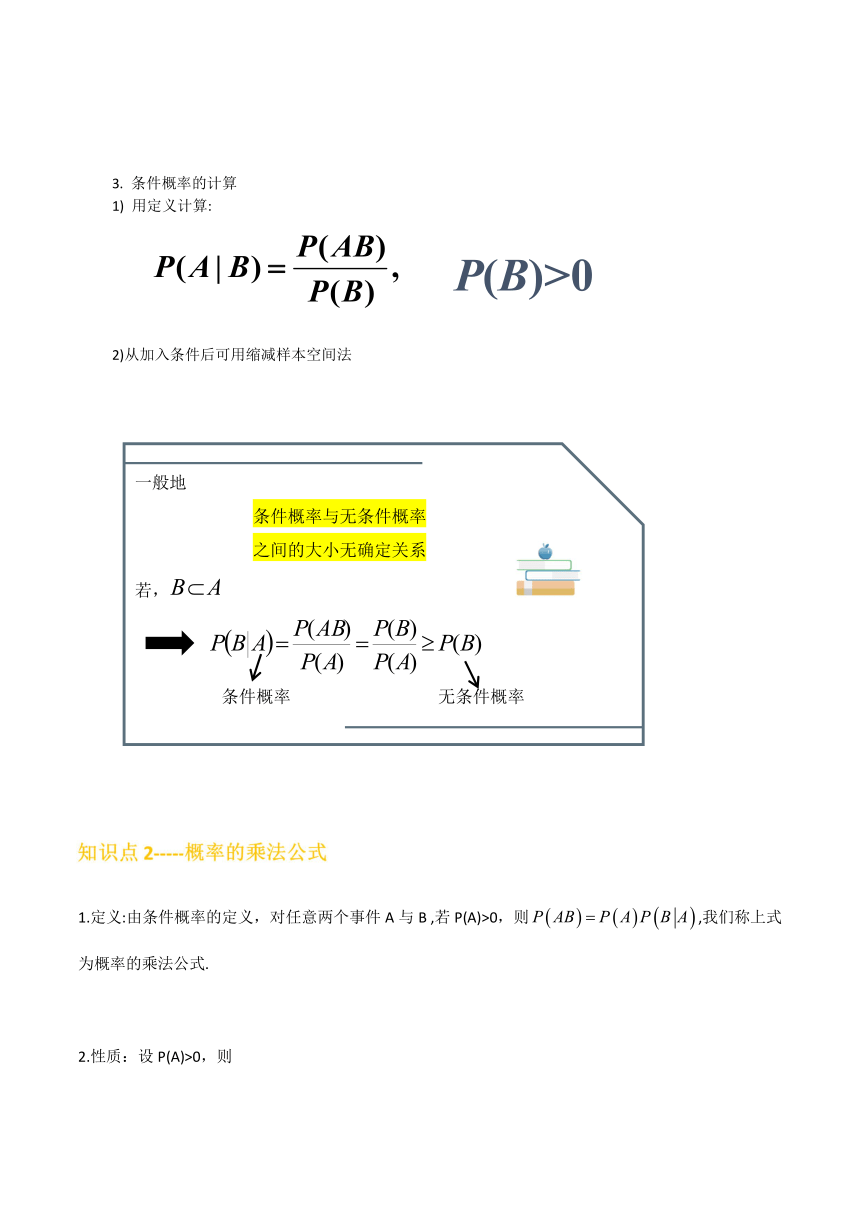
1) 用定义计算:
61912563500P(B)>0
P(B)>0
2)从加入条件后可用缩减样本空间法
405130213995一般地
条件概率与无条件概率
之间的大小无确定关系
若,false
false
条件概率 无条件概率
一般地
条件概率与无条件概率
之间的大小无确定关系
若,false
false
条件概率 无条件概率
34029651333500152971512706356007101077595
38176206350
-95885189230 知识点2-----概率的乘法公式
知识点2-----概率的乘法公式
1.定义:由条件概率的定义,对任意两个事件A与B ,若P(A)>0,则false,我们称上式为概率的乘法公式.
2.性质:设P(A)>0,则
(1)false
(2)如果B与C是两个互斥事件,则false
(3)设false和false互为对立事件,则false
643255146685注意:
由条件概率的定义:
若已知P(B), P(A|B)时, 可以反求P(AB)
定理若P(B)>0,则P(AB)=P(B)P(A|B) (2)
若P(A)>0,则P(AB)=P(A)P(B|A) (3)
注意:
由条件概率的定义:
若已知P(B), P(A|B)时, 可以反求P(AB)
定理若P(B)>0,则P(AB)=P(B)P(A|B) (2)
若P(A)>0,则P(AB)=P(A)P(B|A) (3)
84963019050
-95885138430 知识点2-----全概率公式
知识点2-----全概率公式
1.全概率公式
一般地,设false是一组两两互斥的事件,false,且false,false,则对任意的事件false,有false我们称上面的公式为全概率公式,全概率公式是概率论中最基本的公式之一
注意:
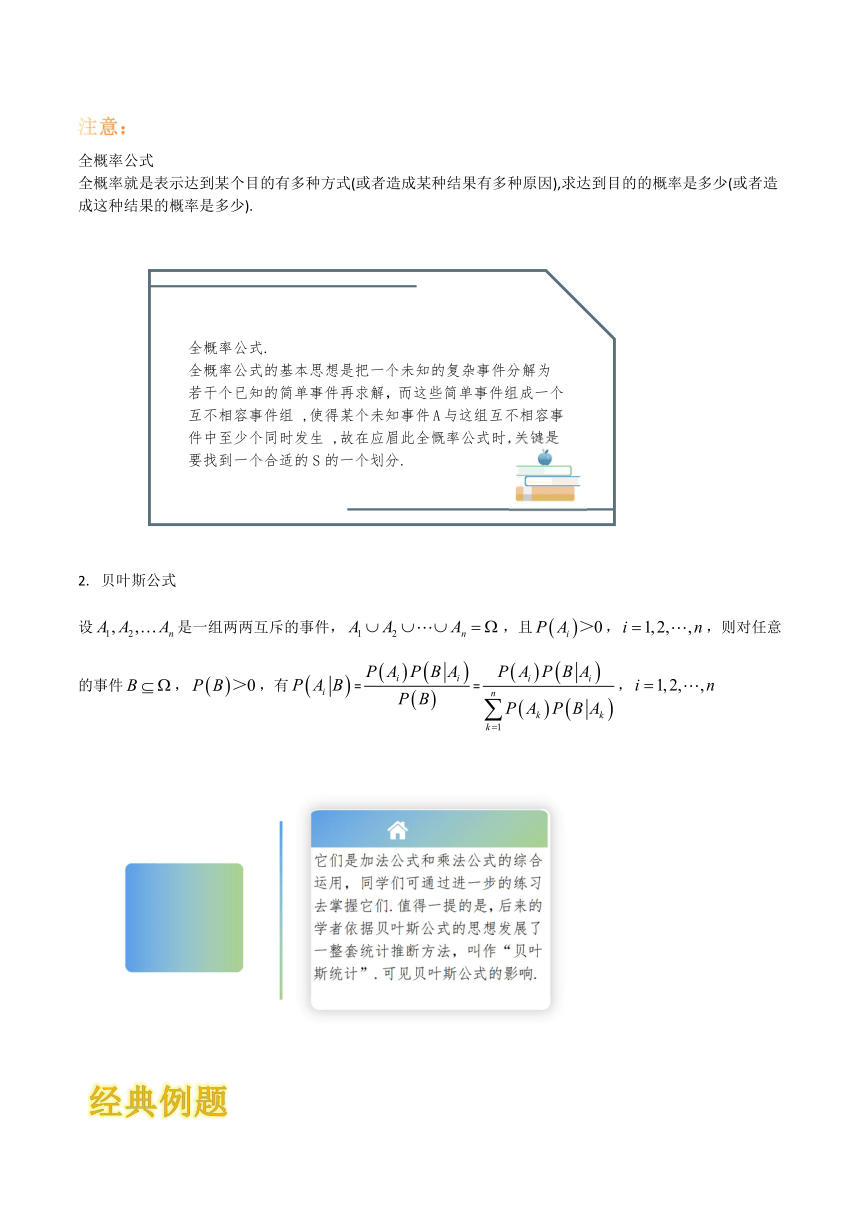
全概率公式
全概率就是表示达到某个目的有多种方式(或者造成某种结果有多种原因),求达到目的的概率是多少(或者造成这种结果的概率是多少).
62801577470全概率公式.
全概率公式的基本思想是把一个未知的复杂事件分解为若干个已知的简单事件再求解,而这些简单事件组成一个 互不相容事件组 ,使得某个未知事件A与这组互不相容事件中至少个同时发生 ,故在应眉此全慨率公式时,关键是要找到一个合适的S的一个划分.
全概率公式.
全概率公式的基本思想是把一个未知的复杂事件分解为若干个已知的简单事件再求解,而这些简单事件组成一个 互不相容事件组 ,使得某个未知事件A与这组互不相容事件中至少个同时发生 ,故在应眉此全慨率公式时,关键是要找到一个合适的S的一个划分.
3810000171450
贝叶斯公式
设false是一组两两互斥的事件,false,且false,false,则对任意的事件false,false,有false=false=false,false
它们是加法公式和乘法公式的综合运用,同学们可通过进一步的练习去掌握它们.值得一提的是,后来的学者依据贝叶斯公式的思想发展了一整套统计推断方法,叫作“贝叶斯统计”.可见贝叶斯公式的影响.
它们是加法公式和乘法公式的综合运用,同学们可通过进一步的练习去掌握它们.值得一提的是,后来的学者依据贝叶斯公式的思想发展了一整套统计推断方法,叫作“贝叶斯统计”.可见贝叶斯公式的影响.
00经典例题
经典例题
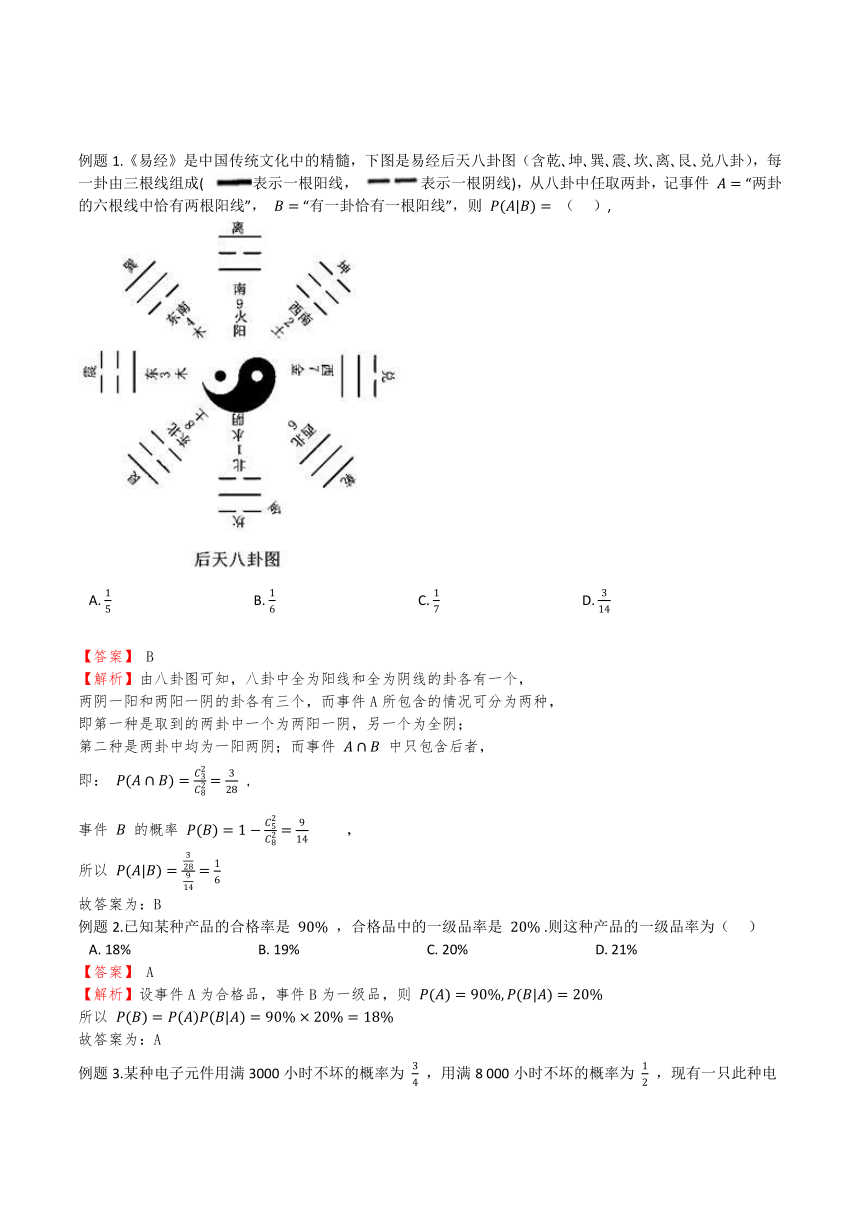
例题1.《易经》是中国传统文化中的精髓,下图是易经后天八卦图(含乾?坤?巽?震?坎?离?艮?兑八卦),每一卦由三根线组成( 表示一根阳线, 表示一根阴线),从八卦中任取两卦,记事件 A= “两卦的六根线中恰有两根阳线”, B= “有一卦恰有一根阳线”,则 P(A|B)= (??? ),
A.?15?????????????????????????????????????????B.?16?????????????????????????????????????????C.?17?????????????????????????????????????????D.?314
【答案】 B
【解析】由八卦图可知,八卦中全为阳线和全为阴线的卦各有一个,
两阴一阳和两阳一阴的卦各有三个,而事件A所包含的情况可分为两种,
即第一种是取到的两卦中一个为两阳一阴,另一个为全阴;
第二种是两卦中均为一阳两阴;而事件 A∩B 中只包含后者,
即: P(A∩B)=C32C82=328 ,
事件 B 的概率 P(B)=1?C52C82=914 ,
所以 P(A|B)=328914=16
故答案为:B
例题2.已知某种产品的合格率是 90% ,合格品中的一级品率是 20% .则这种产品的一级品率为(??? )
A.?18%?????????????????????????????????????B.?19%?????????????????????????????????????C.?20%?????????????????????????????????????D.?21%
【答案】 A
【解析】设事件A为合格品,事件B为一级品,则 P(A)=90%,P(B|A)=20%
所以 P(B)=P(A)P(B|A)=90%×20%=18%
故答案为:A
例题3.某种电子元件用满3000小时不坏的概率为 34 ,用满8 000小时不坏的概率为 12 ,现有一只此种电子元件,已经用满3000小时不坏,还能用满8000小时的概率是(?? )
A.?34??????????????????????????????????????????B.?23??????????????????????????????????????????C.?12??????????????????????????????????????????D.?13
【答案】 B
【解析】记事件 A “用满 3000 小时不坏”, P(A)=34
记事件 B “用满 8000 小时不坏, P(B)=12
∵B?A,∴P(AB)=P(B)=12
则 P(B|A)=P(AB)P(A)=1234=12×43=23
故答案为:B
例题4.某校将进行篮球定点投篮测试,规则为:每人至多投3次,先在 M 处投一次三分球,投进得3分,未投进不得分,以后均在 N 处投两分球,每投进一次得2分,未投进不得分.测试者累计得分高于3分即通过测试,并终止投篮.甲、乙两位同学为了通过测试,进行了五轮投篮训练,每人每轮在 M 处和 N 处各投10次,根据他们每轮两分球和三分球的命中次数情况分别得到如图表:
若以每人五轮投篮训练命中频率的平均值作为其测试时每次投篮命中的概率.
(1)求甲同学通过测试的概率;
(2)在甲、乙两位同学均通过测试的条件下,求甲得分比乙得分高的概率.
【答案】 (1)解:甲同学两分球投篮命中的概率为 510+410+310+610+7105=0.5 ,
甲同学三分球投篮命中的概率为 110+0+110+210+1105=0.1 ,
设甲同学累计得分为 X ,
则 P(X≥4)=P(X=4)+P(X=5)=0.9×0.5×0.5+0.1×0.5+0.1×0.5×0.5=0.3 ,
所以,甲同学通过测试的概率为0.3
(2)解:乙同学两分球投篮命中率为 210+410+310+510+6105=0.4 ,
乙同学三分球投篮命中率为 110+210+310+110+3105=0.2 .
设乙同学累计得分为 Y ,则 P(Y=4)=0.8×0.4×0.4=0.128 ,
P(Y=5)=0.2×0.4+0.2×0.6×0.4=0.128 ,
设“甲得分比乙得分高”为事件 A ,“甲、乙两位同学均通过了测试”为事件 B ,
则 P(AB)=P(X=5)?P(Y=4)=0.075×0.128=0.0096 ,
P(B)=[P(X=4)+P(X=5)]?[P(Y=4)+P(Y=5)]=0.0768 ,
由条件概率公式可得 P(A|B)=P(AB)P(B)=0.00960.0768=18
【解析】(1)分别求出甲同学两分球投篮命中的概率和甲同学三分球投篮命中的概率,设甲同学累计得分为X,则P(X≥4)=P(X=4)+P(X=5),由此能求出甲同学通过测试的概率;
(2)乙同学两分球投篮命中的概率为0.4,三分球投篮命中的概率为0.2,设乙同学累计得分为Y,求出P(Y=4)=0.128,P(Y=5)=0.128,设“甲得分比乙得到高”为事件A,“甲、乙两位同学均通过了测试”为事件B,则P(AB)=P(X=5)?P(X=4),P(B)=[P(X=4)+P(X=5)]?[P(Y=4)+P(Y=5)],由条件概率得: P(A|B)=P(AB)P(B)=0.00960.0768=18。
例题5已知某电脑卖家只卖甲、乙两个品牌的电脑,其中甲品牌的电脑占70%.甲品牌的电脑中,优质率为80%;乙品牌的电脑中,优质率为90%.从该电脑卖家中随机购买一台电脑;
(1)求买到优质电脑的概率;
(2)若已知买到的是优质电脑,求买到的是甲品牌电脑的概率(精确到0.1%).
【答案】 (1)解:从该电脑卖家中随机购买一台电脑,为甲品牌优质电脑的概率为 70%×80%=0.56
为乙品牌优质电脑的概率为 (1?70%)×90%=0.27 ,所以买到优质电脑的概率为 0.56+0.27=0.83,
(2)解:买到的是甲品牌电脑的概率为 0.560.56+0.27≈0.675
【解析】(1)根据相互独立事件的概率,即可求出相应的概率;
(2)根据条件概率的计算公式求出相应的概率.
86995165735随堂练习
随堂练习
练习1.甲罐中有5个红球,2个白球和3个黑球,乙罐中有6个红球,2个白球和2个黑球,先从甲罐中随机取岀一个球放入乙罐,分别以 A1 , A2 , A3 表示由甲罐取岀的球是红球、白球和黑球的事件,再从乙罐中随机取出一个球,以 B 表示由乙罐取出的球是红球的事件,下列结论中不正确的是(??? )
A.?事件 B 与事件 A1 不相互独立?????????????????????????????B.?A1 , A2 , A3 是两两互斥的事件
C.?P(B)=35???????????????????????????????????????????????????????????D.?P(B|A1)=711
练习2.如图所示,半径为1的圆 O 是正方形 MNPQ 的内切圆,将一颗豆子随机地扔到正方形 MNPQ 内,用 A 表示事件“豆子落在圆 O 内”, B 表示事件“豆子落在扇形 OEF (阴影部分)内”,则 P(B|A)= ( ??)
?π4????????????????????????????????????????B.?14????????????????????????????????????????C.?π16????????????????????????????????????????D.?18
练习3.如图, ΔABC 和 ΔDEF 都是圆内接正三角形,且 BC//EF ,将一颗豆子随机地扔到该圆内,用 A 表示事件“豆子落在 ΔABC 内”, B 表示事件“豆子落在 ΔDEF 内”,则 P(B|A)= (??? )
A.?334π??????????????????????????????????????B.?32π??????????????????????????????????????C.?13??????????????????????????????????????D.?23
练习4.在女子十米跳台比赛中,已知甲、乙两名选手发挥正常的概率分别为0.9,0.85,求:
(1)甲、乙两名选手发挥均正常的概率;
甲、乙两名选手至多有一名发挥正常的概率;
(3)甲、乙两名选手均出现失误的概率.
练习5.某班有6名班干部,其中男生4人,女生2人,任选3人参加学校的义务劳动.
(1)求男生甲或女生乙被选中的概率;
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(A)和P(B|A).
练习6.从一副扑克牌(52张)中任意抽取一张,则:
(1)这张牌是红桃的概率是多少?
(2)这张牌是有人头像(J、Q、K)的概率是多少?
(3)在这张牌是红桃的条件下,有人头像的概率是多少?
229870-76835参考答案
参考答案
练习1
【答案】 C
【解析】A.乙罐取出的球是红球的事件与前面是否取出红球相关,正确
B. A1 , A2 , A3 两两不可能同时发生,正确
C. P(B)=510×711+510×611=1322 ,不正确
D. P(B|A1)=P(BA1)P(A1)=12×71112=711 ,正确
故答案为:C
练习2
【答案】 B
【解析】如图所示,半径为1的圆O是正方形MNPQ的内切圆,
将一颗豆子随机地扔到正方形MNPQ内,
用A表示事件“豆子落在圆O内”,B表示事件“豆子落在扇形 OEF( 阴影部分 ) 内”,
则 P(A)=π×1222=π4 , P(AB)=14×π×1222=π16 , ∴P(B|A)=P(AB)P(A)=π16π4=14 .
故答案为:B .
练习3
【答案】 D
【解析】如图所示,作三条辅助线,
根据已知条件,这些小三角形全等, ΔABC 包含 9 个小三角形,
同时又在 ΔDEF 内的小三角形共有 6 个,
所以 P(B|A)= 69=23 ,
故答案为:D.
练习4
【答案】 (1)解:设事件A,B分别表示甲、乙两名选手发挥正常,由题意可知,事件A,B相互独立,且P(A)=0.9,P(B)=0.85.
两名选手发挥均正常的概率P=P(AB)=P(A)P(B)=0.9×0.85=0.765
(2)解:对立事件为“甲、乙两名选手发挥均正常”,故所求事件的概率P=1-P(AB)=1-0.765=0.235
(3)解:依题意可知,所求事件的概率P=P( A B )=P( A )P( B )=(1-P(A))(1-P(B))=(1-0.9)×(1-0.85)=0.015
【解析】设事件A,B分别表示甲、乙两名选手发挥正常,由题意可知,事件A,B相互独立,利用相互独立事件的概率公式,对立事件的概率公式等运算求得结果.
练习5
【答案】 (1)解:某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动,
总的选法有 C63 =20种,男生甲或女生乙被选中的选法有 C21C42+C22C41 =12+4=16种,
∴男生甲或女生乙被选中的概率为 1620 = 45
(2)解:总的选法有 C63 =20种,男生甲被选中的概率为P(A)= C5220=12 ,
男生甲、女生乙都被选中的概率为P(AB)= C4120 = 15 ;
则在男生甲被选中的情况下,求女生乙也被选中的概率为P(B|A)= P(AB)P(A) = 25
【解析】(1)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动,总的选法有 C63 =20,男生甲或女生乙被选中的选法有 C21C42+C22C41 =12+4=16种,由此能求出男生甲或女生乙被选中的概率.(2)总的选法有 C63 =20种,可得男生甲被选中的概率;男生甲被选中的情况下,女生乙也被选中,再从剩余4人中选1人,有4种选法,由此能求出结果.
练习6
【答案】 (1)解:设A表示“任取一张是红桃”,B表示“任取一张是有人头像的”,则
P(A)= 1352=14
(2)解:P(B)= 1252=313
(3)解:“任取一张既是红桃又是有人头像的”为AB,则P(AB)= 352 .任取一张是红桃的条件下,也就是在13张红桃的范围内考虑有人头像的概率是多少,这就是条件概率P(B|A)的值,P(B|A)= P(AB)P(A)=3521352=313
【解析】一副52张(没有大小王)的扑克牌中K有4张,黑色牌有26张,由此求出抽到的这张牌是K或者是黑色牌的基本事件个数,从而利用等可能概率计算公式能求出抽到牌的概率.
第七章随机变量及其分布
1150620711207.1条件概率与全概率公式
7.1条件概率与全概率公式
134620183515 知识点1-----条件概率
知识点1-----条件概率
1.定义:
条件概率揭示了P(A),P(AB),P()三者之间“知二求一”的关系
一般地,设A,B为两个随机事件,且P(A)>0,我们称P()=为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
2. 条件概率的定义
设A、B是两个事件,且P(B)>0,则称
false
为在事件B发生的条件下,事件A的条件概率.若事件B已发生, 则为使 A也发生 , 试验结果必须是既在 B 中又在A中的样本点 , 即此点必属于AB. 由于我们已经知道B已发生, 故B变成了新的样本空间 , 于是有了以上公式
条件概率的计算
1) 用定义计算:
61912563500P(B)>0
P(B)>0
2)从加入条件后可用缩减样本空间法
405130213995一般地
条件概率与无条件概率
之间的大小无确定关系
若,false
false
条件概率 无条件概率
一般地
条件概率与无条件概率
之间的大小无确定关系
若,false
false
条件概率 无条件概率
34029651333500152971512706356007101077595
38176206350
-95885189230 知识点2-----概率的乘法公式
知识点2-----概率的乘法公式
1.定义:由条件概率的定义,对任意两个事件A与B ,若P(A)>0,则false,我们称上式为概率的乘法公式.
2.性质:设P(A)>0,则
(1)false
(2)如果B与C是两个互斥事件,则false
(3)设false和false互为对立事件,则false
643255146685注意:
由条件概率的定义:
若已知P(B), P(A|B)时, 可以反求P(AB)
定理若P(B)>0,则P(AB)=P(B)P(A|B) (2)
若P(A)>0,则P(AB)=P(A)P(B|A) (3)
注意:
由条件概率的定义:
若已知P(B), P(A|B)时, 可以反求P(AB)
定理若P(B)>0,则P(AB)=P(B)P(A|B) (2)
若P(A)>0,则P(AB)=P(A)P(B|A) (3)
84963019050
-95885138430 知识点2-----全概率公式
知识点2-----全概率公式
1.全概率公式
一般地,设false是一组两两互斥的事件,false,且false,false,则对任意的事件false,有false我们称上面的公式为全概率公式,全概率公式是概率论中最基本的公式之一
注意:
全概率公式
全概率就是表示达到某个目的有多种方式(或者造成某种结果有多种原因),求达到目的的概率是多少(或者造成这种结果的概率是多少).
62801577470全概率公式.
全概率公式的基本思想是把一个未知的复杂事件分解为若干个已知的简单事件再求解,而这些简单事件组成一个 互不相容事件组 ,使得某个未知事件A与这组互不相容事件中至少个同时发生 ,故在应眉此全慨率公式时,关键是要找到一个合适的S的一个划分.
全概率公式.
全概率公式的基本思想是把一个未知的复杂事件分解为若干个已知的简单事件再求解,而这些简单事件组成一个 互不相容事件组 ,使得某个未知事件A与这组互不相容事件中至少个同时发生 ,故在应眉此全慨率公式时,关键是要找到一个合适的S的一个划分.
3810000171450
贝叶斯公式
设false是一组两两互斥的事件,false,且false,false,则对任意的事件false,false,有false=false=false,false
它们是加法公式和乘法公式的综合运用,同学们可通过进一步的练习去掌握它们.值得一提的是,后来的学者依据贝叶斯公式的思想发展了一整套统计推断方法,叫作“贝叶斯统计”.可见贝叶斯公式的影响.
它们是加法公式和乘法公式的综合运用,同学们可通过进一步的练习去掌握它们.值得一提的是,后来的学者依据贝叶斯公式的思想发展了一整套统计推断方法,叫作“贝叶斯统计”.可见贝叶斯公式的影响.
00经典例题
经典例题
例题1.《易经》是中国传统文化中的精髓,下图是易经后天八卦图(含乾?坤?巽?震?坎?离?艮?兑八卦),每一卦由三根线组成( 表示一根阳线, 表示一根阴线),从八卦中任取两卦,记事件 A= “两卦的六根线中恰有两根阳线”, B= “有一卦恰有一根阳线”,则 P(A|B)= (??? ),
A.?15?????????????????????????????????????????B.?16?????????????????????????????????????????C.?17?????????????????????????????????????????D.?314
【答案】 B
【解析】由八卦图可知,八卦中全为阳线和全为阴线的卦各有一个,
两阴一阳和两阳一阴的卦各有三个,而事件A所包含的情况可分为两种,
即第一种是取到的两卦中一个为两阳一阴,另一个为全阴;
第二种是两卦中均为一阳两阴;而事件 A∩B 中只包含后者,
即: P(A∩B)=C32C82=328 ,
事件 B 的概率 P(B)=1?C52C82=914 ,
所以 P(A|B)=328914=16
故答案为:B
例题2.已知某种产品的合格率是 90% ,合格品中的一级品率是 20% .则这种产品的一级品率为(??? )
A.?18%?????????????????????????????????????B.?19%?????????????????????????????????????C.?20%?????????????????????????????????????D.?21%
【答案】 A
【解析】设事件A为合格品,事件B为一级品,则 P(A)=90%,P(B|A)=20%
所以 P(B)=P(A)P(B|A)=90%×20%=18%
故答案为:A
例题3.某种电子元件用满3000小时不坏的概率为 34 ,用满8 000小时不坏的概率为 12 ,现有一只此种电子元件,已经用满3000小时不坏,还能用满8000小时的概率是(?? )
A.?34??????????????????????????????????????????B.?23??????????????????????????????????????????C.?12??????????????????????????????????????????D.?13
【答案】 B
【解析】记事件 A “用满 3000 小时不坏”, P(A)=34
记事件 B “用满 8000 小时不坏, P(B)=12
∵B?A,∴P(AB)=P(B)=12
则 P(B|A)=P(AB)P(A)=1234=12×43=23
故答案为:B
例题4.某校将进行篮球定点投篮测试,规则为:每人至多投3次,先在 M 处投一次三分球,投进得3分,未投进不得分,以后均在 N 处投两分球,每投进一次得2分,未投进不得分.测试者累计得分高于3分即通过测试,并终止投篮.甲、乙两位同学为了通过测试,进行了五轮投篮训练,每人每轮在 M 处和 N 处各投10次,根据他们每轮两分球和三分球的命中次数情况分别得到如图表:
若以每人五轮投篮训练命中频率的平均值作为其测试时每次投篮命中的概率.
(1)求甲同学通过测试的概率;
(2)在甲、乙两位同学均通过测试的条件下,求甲得分比乙得分高的概率.
【答案】 (1)解:甲同学两分球投篮命中的概率为 510+410+310+610+7105=0.5 ,
甲同学三分球投篮命中的概率为 110+0+110+210+1105=0.1 ,
设甲同学累计得分为 X ,
则 P(X≥4)=P(X=4)+P(X=5)=0.9×0.5×0.5+0.1×0.5+0.1×0.5×0.5=0.3 ,
所以,甲同学通过测试的概率为0.3
(2)解:乙同学两分球投篮命中率为 210+410+310+510+6105=0.4 ,
乙同学三分球投篮命中率为 110+210+310+110+3105=0.2 .
设乙同学累计得分为 Y ,则 P(Y=4)=0.8×0.4×0.4=0.128 ,
P(Y=5)=0.2×0.4+0.2×0.6×0.4=0.128 ,
设“甲得分比乙得分高”为事件 A ,“甲、乙两位同学均通过了测试”为事件 B ,
则 P(AB)=P(X=5)?P(Y=4)=0.075×0.128=0.0096 ,
P(B)=[P(X=4)+P(X=5)]?[P(Y=4)+P(Y=5)]=0.0768 ,
由条件概率公式可得 P(A|B)=P(AB)P(B)=0.00960.0768=18
【解析】(1)分别求出甲同学两分球投篮命中的概率和甲同学三分球投篮命中的概率,设甲同学累计得分为X,则P(X≥4)=P(X=4)+P(X=5),由此能求出甲同学通过测试的概率;
(2)乙同学两分球投篮命中的概率为0.4,三分球投篮命中的概率为0.2,设乙同学累计得分为Y,求出P(Y=4)=0.128,P(Y=5)=0.128,设“甲得分比乙得到高”为事件A,“甲、乙两位同学均通过了测试”为事件B,则P(AB)=P(X=5)?P(X=4),P(B)=[P(X=4)+P(X=5)]?[P(Y=4)+P(Y=5)],由条件概率得: P(A|B)=P(AB)P(B)=0.00960.0768=18。
例题5已知某电脑卖家只卖甲、乙两个品牌的电脑,其中甲品牌的电脑占70%.甲品牌的电脑中,优质率为80%;乙品牌的电脑中,优质率为90%.从该电脑卖家中随机购买一台电脑;
(1)求买到优质电脑的概率;
(2)若已知买到的是优质电脑,求买到的是甲品牌电脑的概率(精确到0.1%).
【答案】 (1)解:从该电脑卖家中随机购买一台电脑,为甲品牌优质电脑的概率为 70%×80%=0.56
为乙品牌优质电脑的概率为 (1?70%)×90%=0.27 ,所以买到优质电脑的概率为 0.56+0.27=0.83,
(2)解:买到的是甲品牌电脑的概率为 0.560.56+0.27≈0.675
【解析】(1)根据相互独立事件的概率,即可求出相应的概率;
(2)根据条件概率的计算公式求出相应的概率.
86995165735随堂练习
随堂练习
练习1.甲罐中有5个红球,2个白球和3个黑球,乙罐中有6个红球,2个白球和2个黑球,先从甲罐中随机取岀一个球放入乙罐,分别以 A1 , A2 , A3 表示由甲罐取岀的球是红球、白球和黑球的事件,再从乙罐中随机取出一个球,以 B 表示由乙罐取出的球是红球的事件,下列结论中不正确的是(??? )
A.?事件 B 与事件 A1 不相互独立?????????????????????????????B.?A1 , A2 , A3 是两两互斥的事件
C.?P(B)=35???????????????????????????????????????????????????????????D.?P(B|A1)=711
练习2.如图所示,半径为1的圆 O 是正方形 MNPQ 的内切圆,将一颗豆子随机地扔到正方形 MNPQ 内,用 A 表示事件“豆子落在圆 O 内”, B 表示事件“豆子落在扇形 OEF (阴影部分)内”,则 P(B|A)= ( ??)
?π4????????????????????????????????????????B.?14????????????????????????????????????????C.?π16????????????????????????????????????????D.?18
练习3.如图, ΔABC 和 ΔDEF 都是圆内接正三角形,且 BC//EF ,将一颗豆子随机地扔到该圆内,用 A 表示事件“豆子落在 ΔABC 内”, B 表示事件“豆子落在 ΔDEF 内”,则 P(B|A)= (??? )
A.?334π??????????????????????????????????????B.?32π??????????????????????????????????????C.?13??????????????????????????????????????D.?23
练习4.在女子十米跳台比赛中,已知甲、乙两名选手发挥正常的概率分别为0.9,0.85,求:
(1)甲、乙两名选手发挥均正常的概率;
甲、乙两名选手至多有一名发挥正常的概率;
(3)甲、乙两名选手均出现失误的概率.
练习5.某班有6名班干部,其中男生4人,女生2人,任选3人参加学校的义务劳动.
(1)求男生甲或女生乙被选中的概率;
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(A)和P(B|A).
练习6.从一副扑克牌(52张)中任意抽取一张,则:
(1)这张牌是红桃的概率是多少?
(2)这张牌是有人头像(J、Q、K)的概率是多少?
(3)在这张牌是红桃的条件下,有人头像的概率是多少?
229870-76835参考答案
参考答案
练习1
【答案】 C
【解析】A.乙罐取出的球是红球的事件与前面是否取出红球相关,正确
B. A1 , A2 , A3 两两不可能同时发生,正确
C. P(B)=510×711+510×611=1322 ,不正确
D. P(B|A1)=P(BA1)P(A1)=12×71112=711 ,正确
故答案为:C
练习2
【答案】 B
【解析】如图所示,半径为1的圆O是正方形MNPQ的内切圆,
将一颗豆子随机地扔到正方形MNPQ内,
用A表示事件“豆子落在圆O内”,B表示事件“豆子落在扇形 OEF( 阴影部分 ) 内”,
则 P(A)=π×1222=π4 , P(AB)=14×π×1222=π16 , ∴P(B|A)=P(AB)P(A)=π16π4=14 .
故答案为:B .
练习3
【答案】 D
【解析】如图所示,作三条辅助线,
根据已知条件,这些小三角形全等, ΔABC 包含 9 个小三角形,
同时又在 ΔDEF 内的小三角形共有 6 个,
所以 P(B|A)= 69=23 ,
故答案为:D.
练习4
【答案】 (1)解:设事件A,B分别表示甲、乙两名选手发挥正常,由题意可知,事件A,B相互独立,且P(A)=0.9,P(B)=0.85.
两名选手发挥均正常的概率P=P(AB)=P(A)P(B)=0.9×0.85=0.765
(2)解:对立事件为“甲、乙两名选手发挥均正常”,故所求事件的概率P=1-P(AB)=1-0.765=0.235
(3)解:依题意可知,所求事件的概率P=P( A B )=P( A )P( B )=(1-P(A))(1-P(B))=(1-0.9)×(1-0.85)=0.015
【解析】设事件A,B分别表示甲、乙两名选手发挥正常,由题意可知,事件A,B相互独立,利用相互独立事件的概率公式,对立事件的概率公式等运算求得结果.
练习5
【答案】 (1)解:某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动,
总的选法有 C63 =20种,男生甲或女生乙被选中的选法有 C21C42+C22C41 =12+4=16种,
∴男生甲或女生乙被选中的概率为 1620 = 45
(2)解:总的选法有 C63 =20种,男生甲被选中的概率为P(A)= C5220=12 ,
男生甲、女生乙都被选中的概率为P(AB)= C4120 = 15 ;
则在男生甲被选中的情况下,求女生乙也被选中的概率为P(B|A)= P(AB)P(A) = 25
【解析】(1)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动,总的选法有 C63 =20,男生甲或女生乙被选中的选法有 C21C42+C22C41 =12+4=16种,由此能求出男生甲或女生乙被选中的概率.(2)总的选法有 C63 =20种,可得男生甲被选中的概率;男生甲被选中的情况下,女生乙也被选中,再从剩余4人中选1人,有4种选法,由此能求出结果.
练习6
【答案】 (1)解:设A表示“任取一张是红桃”,B表示“任取一张是有人头像的”,则
P(A)= 1352=14
(2)解:P(B)= 1252=313
(3)解:“任取一张既是红桃又是有人头像的”为AB,则P(AB)= 352 .任取一张是红桃的条件下,也就是在13张红桃的范围内考虑有人头像的概率是多少,这就是条件概率P(B|A)的值,P(B|A)= P(AB)P(A)=3521352=313
【解析】一副52张(没有大小王)的扑克牌中K有4张,黑色牌有26张,由此求出抽到的这张牌是K或者是黑色牌的基本事件个数,从而利用等可能概率计算公式能求出抽到牌的概率.
