7.5正态分布-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案)
文档属性
| 名称 | 7.5正态分布-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 22:54:31 | ||
图片预览




文档简介
1225550011938000436880-371475第七章随机变量及其分布
第七章随机变量及其分布
17462502178057.5正态分布
7.5正态分布
-101600295910知识点1-----正态分布
知识点1-----正态分布
(1)定义
如果对于任何实数随机变量满足:,则称随机变量服从正态分布。记为
(2)正态分布的期望与方差
若,,则的期望与方差分别为:,。
要点诠释:
(1)正态分布由参数和确定。
参数是均值,它是反映随机变量取值的平均水平的特征数,可用样本的均值去估计。是
标准差,它是衡量随机变量总体波动大小的特征数,可以用样本的标准差去估计。
(2)经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.
在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.
-107950290195知识点2-----正态曲线
知识点2-----正态曲线
1.正态曲线:
沿着横轴方向水平移动只能改变对称轴的位置,曲线的形状没有改变, 所得的曲线依然是正态曲线false函数,其中false,false为参数.
显然对于任意x∈R,false,它的图象在x轴的上方,可以证明x轴和曲线之间的区域的面积为1,我们称false为正态密度函数,称它的图象为正态分布密度曲线,简称正态曲线.若随机变量X的概率密度函数为false,则称随机变量X服从正态分布,记为X~false,特别地,当=0,=1时,称随机变量X服从标准正态分布.
2.正态曲线的性质:
①曲线位于轴上方,与轴不相交;
②曲线是单峰的,它关于直线对称;
③曲线在时达到峰值;
④当时,曲线上升;当时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
⑤曲线与轴之间的面积为1;
⑥决定曲线的位置和对称性;
当一定时,曲线的对称轴位置由确定;如下图所示,曲线随着的变化而沿轴平移。
⑦确定曲线的形状;
当一定时,曲线的形状由确定。越小,曲线越“高瘦”,表示总体的分布越集中;越大,曲线越“矮胖”,表示总体的分布越分散。如下图所示。
要点诠释:
性质①说明了函数具有值域(函数值为正)及函数的渐近线(x轴).性质②并且说明了函数具有对称性;性质③说明了函数在x=时取最值;性质⑦说明越大,总体分布越分散,越小,总体分布越集中.
4762522860 重难点探究
重难点探究
随机变量取值的概率与面积的关系
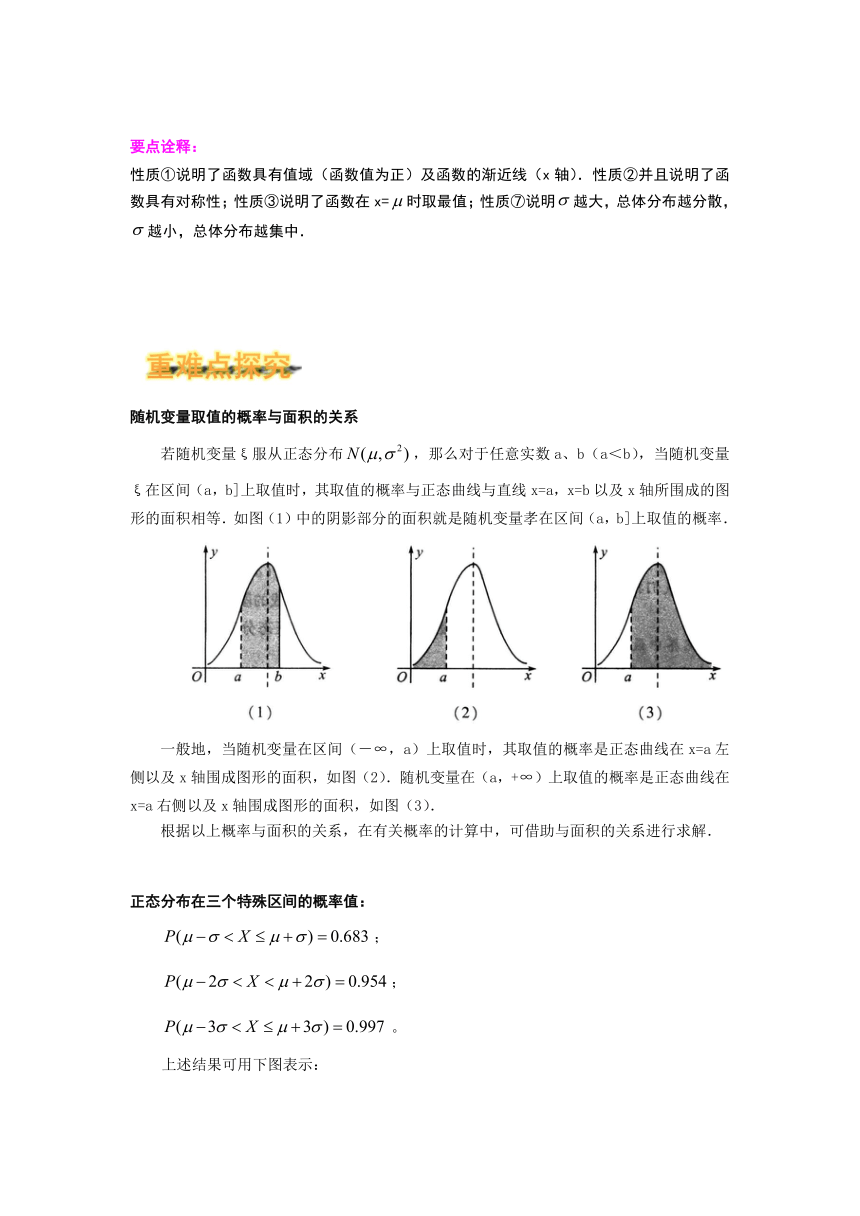
若随机变量ξ服从正态分布,那么对于任意实数a、b(a<b),当随机变量ξ在区间(a,b]上取值时,其取值的概率与正态曲线与直线x=a,x=b以及x轴所围成的图形的面积相等.如图(1)中的阴影部分的面积就是随机变量孝在区间(a,b]上取值的概率.
一般地,当随机变量在区间(-∞,a)上取值时,其取值的概率是正态曲线在x=a左侧以及x轴围成图形的面积,如图(2).随机变量在(a,+∞)上取值的概率是正态曲线在x=a右侧以及x轴围成图形的面积,如图(3).
根据以上概率与面积的关系,在有关概率的计算中,可借助与面积的关系进行求解.
正态分布在三个特殊区间的概率值:
;
;
。
上述结果可用下图表示:
要点诠释:
若随机变量服从正态分布,则落在内的概率约为,落在之外的概率约为,一般称后者为小概率事件,并认为在一次试验中,小概率事件几乎不可能发生。
一般的,服从于正态分布的随机变量通常只取之间的值,简称为原则。
求正态分布在给定区间上的概率方法
(1)数形结合,利用正态曲线的对称性及曲线与轴之间面积为1。
①正态曲线关于直线对称,与对称的区间上的概率相等。
例如;
②;
③若,则。
(2)利用正态分布在三个特殊区间内取值的概率:
①;
②;
③。
00经典例题
经典例题
例题1.已知随机变量 ξ~N(μ,σ2) ,有下列四个命题:
甲: P(ξP(ξ>a+2) ? 乙: P(ξ>a)=0.5
丙: (ξ≤a)=0.5 ? 丁: P(a<ξ如果只有一个假命题,则该命题为(??? )
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
【答案】 D
【解析】由于乙、丙的真假性相同,所以乙、丙都是真命题,故 a=μ ,
根据正态分布的对称性可知:甲: P(ξ<μ?1)>P(ξ>μ+2) 为真命题,所以丁为假命题.
并且, P(μ<ξ<μ+1)>P(μ+1<ξ<μ+2) .
所以假命题的是丁.
故为:D
例题2.某种芯片的良品率 X 服从正态分布 N(0.95,0.012) ,公司对科技改造团队的奖励方案如下:若芯片的良品率不超过 95% ,不予奖励;若芯片的良品率超过 95% 但不超过 96% ,每张芯片奖励 100 元;若芯片的良品率超过 96% ,每张芯片奖励 200 元.则每张芯片获得奖励的数学期望为(??? )元附:随机变量 ξ 服从正态分布 N(μ,σ2) ,则 P(μ?σ<ξ<μ+σ)=0.6826 , P(μ?2σ<ξ<μ+2σ)=0.9544 , P(μ?3σ<ξ<μ+3σ)=0.9974 .
A.?52.28??????????????????????????????????B.?65.87??????????????????????????????????C.?50.13??????????????????????????????????D.?131.74
【答案】 B
【解析】因为 X?N(0.95,0.012) ,得出 μ=0.95 , μ+σ=0.96 ,
所以 P(X≤0.95)=P(X≤μ)=0.5 ,
P(0.95=12P(μ?σP(X>0.96)=12[1?P(μ?σ所以 E(X)=0+100×0.3413+200×0.1587=65.87 (元)
故答案为:B
例题3.国家发展改革委、住房城乡建设部于2017年发布了《生活垃圾分类制度实施方案》,规定46个重点城市在2020年底实施生活垃圾强制分类,垃圾回收、利用率要达35%以上.截至2019年底,这46个重点城市生活垃圾分类的居民小区覆盖率已经接近70%.某市在实施垃圾分类之前,从本市人口数量在两万人左右的320个社区中随机抽取50个社区,对这50个社区某天产生的垃圾量(单位:吨)进行了调查,得到如下频数分布表,并将人口数量在两万人左右的社区产生的垃圾数量超过28(吨/天)的确定为“超标”社区:
垃圾量 X
[12.5,15.5)
[15.5,18.5)
[18.5,21.5)
[21.5,24.5)
[24.5,27.5)
[27.5,30.5)
[30.5,33.5)
频数
5
6
9
12
8
6
4
附:若随机变量 X 服从正态分布 N(μ,σ2) ,则 P(μ?σ(1)在频数分布表中,以各组的区间中点值代表该组的各个值,求这50个社区这一天产生的垃圾量的平均值 x (精确到0.1);
(2)若该市人口数量在两万人左右的社区一天产生的垃圾量 X 大致服从正态分布 N(μ,σ2) ,其中 μ , σ2 分别近似为(1)中样本的平均值 x ,方差 s2 ,经计算 s 约为5.2.请利用正态分布知识估计这320个社区一天中“超标”社区的个数;
(3)通过研究样本原始数据发现,抽取的50个社区中这一天共有8个“超标”社区,市政府决定对这8个“超标”社区的垃圾来源进行跟踪调查,现计划在这8个“超标”社区中随机抽取5个进行跟踪调查,设 Y 为抽到的这一天产生的垃圾量 至少为30.5吨的社区个数,求 Y 的分布列与数学期望.
【答案】 (1)解:由频数分布表得
x=14×5+17×6+20×9+23×12+26×8+29×6+32×450
=22.76≈22.8 ,
所以这50个社区这一天产生的垃圾量的平均值为22.8吨
(2)解:由(1)知 μ=22.8 .因为 s 约为5.2,所以取 σ=5.2 .
所以 P(X>28)=P(X>μ+σ)
=1?0.68272=0.15865 .
又 320×0.15865=50.768≈51 ,
所以估计这320分社区一天中“超标”社区的个数为51
(3)解:由频数分布表知:8个“超标”社区中这一天产生的垃圾量至少为30.5吨的社区有4个,所以 Y 的可能取值为1,2,3,4,
P(Y=1)=C41C44C85=114 ,
P(Y=2)=C42C43C85=37 ,
P(Y=3)=C43C42C85=37 ,
P(Y=4)=C44C41C85=114 ,
所以 Y 的分布列为
Y
1
2
3
4
P
114
37
37
114
所以 E(Y)=1×114+2×37+3×37+4×114=52
【解析】(1)利用图表中的数据算平均数的方法可以直接计算出来;
(2)根据正态分布的规律,计算公式可以直接计算出结果;
(3)由题意可知Y可以取值1,2,3,4,再由超几何分布概率的计算方法分别计算出对应的概率,即可计算出结果.
?
例题4.标准的医用外科口罩分三层,外层有防水作用,可防止飞来进入口罩里面,中间层有过滤作用,对于直径小于5微米的颗粒阻隔率必须大于90%,近口鼻的内层可以吸湿,根据国家质量监督检验标准,过滤率是重要的参考标准,为了监控某条口罩生产线的生产过程,检验员每天从该生产线上随机抽取10个口罩,并检验过滤率.根据长期生产经验,可以认为这条生产线正常状态下生产的口罩的过滤率 z 服从正态分布 N(μ,σ2) .
(附:若随机变量 X 服从正态分布 N(μ,σ2) ,则① P(μ?σ(1)假设生产状态正常,记 X 表示一天内抽取的10个口罩中过滤率小于 μ?3σ 的数量,求 P(X≥1) 及 X 的数学期望;
(2)下面是检验员在一天内抽取的10个口罩的过滤率:
1
2
3
4
5
6
7
8
9
10
0.9376
0.9121
0.9424
0.9572
0.9518
0.9058
0.9216
0.9171
0.9635
0.9268
经计算得: x=110i=110xi=0.9335 , s=110i=110(xi?x)2≈0.0189 (其中 xi 为抽取的第 i 个口罩的过滤率)用样本平均数 x 作为 μ 的估计值,用样本标准差 s 作为 σ 的估计值,利用该正态分布,求 P(z≥0.9524) (精确到 0.001 )
【答案】 (1)解:已知检验率服从正态分布 N(μ,σ2) ,则事件 P(X<μ?3σ)=1?0.99742=0.0013
当生产状态正常时,重复不放回的取10个口罩属于独立重复事件, n=10 , p=0.0013 ,
故有: E(X)=np=10×0.0013=0.013 ,
而 P(X≥1)=1?P(X=0)=1?C100p0(1?p)10=1?0.998710=0.0129 .
(2)解:由题意知:由平均数近似估计 μ ,
则有 P(z≥0.9524)=P(z≥x+s)=1?0.68262=0.1587 .
【解析】(1)已知可知检验率服从正态分布 N(μ,σ2)? ,通过PX=0可求出 P(X≥1)=1?P(X=0)≈0.0129?,利用二项分布的期望公式计算可得结论;
(2)利用公式即可得到结论。
-5588038100随堂练习
随堂练习
练习1.某校一次高三年级数学检测,经抽样分析,成绩 ξ 占近似服从正态分布 N(95,σ2) ,且 P(91<ξ≤95)=0.25 .若该校有700人参加此次检测,估计该校此次检测数学成绩不低于99分的人数为(??? )
A.?100??????????????????????????????????????B.?125??????????????????????????????????????C.?150??????????????????????????????????????D.?175
练习2.某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数为 f(x)=12π?10e?(x?80)2200(x∈R) ,则下列命题中不正确的是(??? )
A.?分数在110分以上的人数与分数在50分以下的人数相同
B.?该市这次考试的数学平均成绩 μ 为80分
C.?该市这次考试的数学成绩的标准差 σ 为10
D.?可以简记为:数学成绩服从正态分布 N(80,10)
练习3.已知随机变量 X?N(2,1) ,其正态分布密度曲线如图所示,若向长方形 OABC 中随机投掷1点,则该点恰好落在阴影部分的概率为(??? )(附:若随机变量 ξ?N(μ,σ2) ,则 P(μ?σ<ξ≤μ+σ)=0.6826 , P(μ?2σ<ξ≤μ+2σ)=0.9544 .)
A.?0.1359???????????????????????????????B.?0.7282???????????????????????????????C.?0.8641???????????????????????????????D.?0.93205
练习4.某单位招考工作人员,须参加初试和复试,初试通过后组织考生参加复试,共5000人参加复试,复试共三道题,第一题考生答对得3分,答错得0分,后两题考生每答对一道题得5分,答错得0分,答完三道题后的得分之和为考生的复试成绩.
(1)通过分析可以认为考生初试成绩 X 服从正态分布 N(μ,δ2) ,其中 μ=64 , δ2=169 ,试估计初试成绩不低于90分的人数;
(2)已知某考生已通过初试,他在复试中第一题答对的概率为 34 ,后两题答对的概率均为 23 ,且每道题回答正确与否互不影响.记该考生的复试试成绩为 Y ,求 Y 的分布列及数学期望.
附:若随机变量 X 服从正态分布 N(μ,δ2) ,则 P(μ?δ
练习5.《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为 3% 、 7% 、 16% 、 24% 、 24% 、 16% 、 7% 、 3% .选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到 [91,100] 、 [81,90] 、 [71,80] 、 [61,70] 、 [51,60] 、 [41,50] 、 [31,40] 、 [21,30] 八个分数区间,得到考生的等级成绩.某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布 N(60,169) .
(1)求物理原始成绩在区间 (47,86) 的人数;
(2)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间 [61,80] 的人数,求X的分布列和数学期望.
(附:若随机变量 ξ~N(μ,σ2) ,则 P(μ?σ<ξ<μ+σ)=0.682 , P(μ?2σ<ξ<μ+2σ)=0.954 , P(μ?3σ<ξ<μ+3σ)=0.997 )
练习6.“全面小康路上一个也不能少”是习近平总书记向全国人民作出的郑重承诺!是对全面建成小康社会的形象表达,其中一个重要指标,就是到2020年我国现行标准下农村贫困人口全面脱贫.目前,全国还有一些贫困县未摘帽,不少贫困村未出列,建档立卡贫困人口尚未全部脱贫.某市为了制定下一步扶贫战略,统计了全市1000户农村贫困家庭的年纯收入,并绘制了如下频率分布直方图:
(1)若这1000户家庭中,家庭年纯收入不低于5(千元)的家庭,且不超过7(千元)的户数为40户,请补全频率分布图,并求出这1000户家庭的年纯收入的平均值 X (同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为这1000户的家庭年纯收入 X 服从正态分布 N(μ,σ2) ,其中 μ 近似为年纯收入的平均值 X,σ2 近似为样本方差,经计算知 σ2=9.26 ;设该市的脱贫标准为家庭年纯收入为 x 千元(即家庭年纯收入大于 x 千元,则该户家庭实现脱贫,否则未能脱贫),若根据此正态分布估计,这1000户家庭中有841.35户家庭实现脱贫,试求该市的脱贫标准 x ;
(3)若该市为了加大扶贫力度,拟投入一笔资金,帮助未脱贫家庭脱贫,脱贫家庭巩固脱贫成果,真正做到“全面小康路上一个也不能少”,方案如下:对家庭年纯收入不超过5.92千元的家庭每户家庭给予扶持资金15千元,对家庭年纯收入超过5.92千元,但不超过8.96千元的家庭每户家庭给予扶持资金12千元,对家庭年纯收入超过8.96千元,但不超过15.04千元的家庭每户家庭给予扶持资金8千元,对家庭年纯收入超过15.04千元的家庭不予以资金扶持,设 Y 为每户家庭获得的扶持资金,求 E(Y) (结果精确到0.001).
附:若随机变量 X~N(μ,?σ2) ,则 P(μ?σ
150495-262890参考答案
参考答案
练习1【答案】 D
【解析】由题意,成绩 X 近似服从正态分布 N(95,σ2) ,
则正态分布曲线的对称轴为 X=95 ,
又由 P(91<ξ≤95)=0.25 ,
根据正态分布曲线的对称性,可得 P(X≥99)=12×[1?2×P(91所以该市某校有700人中,估计该校数学成绩不低于99分的人数为 700×0.25=175 人,
故答案为:D.
练习2【答案】 D
【解析】由 f(x)=12π?10e?(x?80)2200(x∈R) ,可得该正态分布为 N(80,100) ,
所以分数在110分以上的人数与分数在50分以下的人数相同,
该市这次考试的数学平均成绩 μ 为80分,标准差 σ 为10。
故答案为:D
练习3【答案】 D
【解析】解:根据题意,随机变量满足正态分布 X?N(2,1) ,
得 μ=2,σ2=1 ,则对称轴为 x=2 , σ=1 ,
根据正态分布密度曲线的对称性,可得:
P(0≤X≤1)=12[P(0≤X≤4)?P(1≤X≤3)]
即 P(0≤X≤1)=12[P(μ?2σ≤X≤μ+2σ)?P(μ?σ≤X≤μ+σ)]
=12×(0.9544?0.6826)=0.1359 ,
可知长方形 OABC 的面积为: 1×2=2 ,设阴影部分的为 S ,
故所求的概率为 P=S2=2?0.13592=0.93205 .
即向长方形 OABC 中随机投掷1点,则该点恰好落在阴影部分的概率为0.93205.
故答案为:D.
练习4【答案】 (1)解:∵学生笔试成绩 X 服从正态分布 N(μ,δ2) ,其中 μ=64 , δ2=169 ,
μ+2δ=64+2×13=90
∴ P(X≥90)=P(X≥μ+2δ)=12(1?0.9544)=0.0228
∴估计笔试成绩不低于90分的人数为 0.0228×5000=114 人
(2)解: Y 的取值分别为0,3,5,8,10,13,
则 P(Y=0)=(1?34)×(1?23)2=136
P(Y=3)=34×(1?23)2=336=112
P(Y=5)=(1?34)×C21×23×(1?23)=19
P(Y=8)=34×C21×23×(1?23)=39=13
P(Y=10)=(1?34)×(23)2=19
P(Y=13)=34×(23)2=39=13
Y 的分布为
故 ξ 的分布列为:
Y
0
3
5
8
10
13
P
136
112
19
13
19
13
E(Y)=0×136+3×112+5×19+8×13+10×19+13×13=32136=10712
【解析】(1)利用正态分布的数据代入数值计算出结果即可。
(2)首先求出满足题意的Y的取值,然后再求出对应Y的值的概率值,由此得到Y的分布,再把数值代入到数学期望的公式计算出结果即可。
练习5【答案】 (1)解:因为物理原始成绩 ξ?N(60,132) ,
所以 P(47<ξ<86)=P(47<ξ<60)+P(60≤ξ<86)
=12P(60?13<ξ<60+13)+12P(60?2×13≤ξ<60+2×13)
=0.6822+0.9542
=0.818 .
所以物理原始成绩在(47,86)的人数为 2000×0.818=1636 (人).
(2)解:由题意得,随机抽取1人,其成绩在区间[61,80]内的概率为 25 .
所以随机抽取三人,则 X 的所有可能取值为0,1,2,3,且 X?B(3,25) ,
所以 P(X=0)=(35)3=27125 ,
P(X=1)=C31?25?(35)2=54125 ,
P(X=2)=C32?(25)2?35=36125 ,
? P(X=3)=(25)3=8125 .
所以 X 的分布列为
X
0
1
2
3
P
27125
54125
36125
8125
所以数学期望 E(X)=3×25=65 .
【解析】(Ⅰ)根据正态曲线的对称性,可将区间 (47,86) 分为 (47,60) 和 (60,86) 两种情况,然后根据特殊区间上的概率求出成绩在区间 (47,86) 内的概率,进而可求出相应的人数;(Ⅱ)由题意得成绩在区间[61,80]的概率为 25 ,且 X?B(3,25) ,由此可得X的分布列和数学期望.
练习6【答案】 (1)解:家庭年纯收入不低于5(千元)且不超过7(千元)的频率为 401000=0.04 ,
纵坐标为0.02;家庭年纯收入超过15(千元),但不超过17(千元)的家庭频率为
1?2×(0.02+0.05+0.12+0.16+0.06+0.04)=0.1 ,纵坐标为0.05,
补全频率分布直方图如下图:
这1000户家庭的年纯收入的平均值为: 6×0.04+8×0.1+10×0.24+12×0.32+14×0.12+16×0.1+18×0.08=12 .
(2)解:1000户家庭中有841.35户家庭实现脱贫,
则未脱贫概率为 1?841.351000=0.15865 ,
设该市的脱贫标准为 x ,则 P(x根据 P(μ?σ得脱贫标准 x=μ?σ=12?9.26=12?3.04=8.96 .
(3)解: ∵μ=12,σ=9.26=3.04,∴μ?2σ=5.92 ,
μ?σ=8.96,μ+σ=15.04 ,
家庭年纯收入不超过5.92千元的家庭频率为
P(X<5.92)=P(X<μ?2σ)=1?0.95452≈0.0228 ,
家庭年纯收入超过5.92千元,但不超过8.96千元的家庭频率为
P(5.92家庭年纯收入超过8.96千元,但不超过15.04千元的家庭频率为
P(8.96家庭年纯收入超过15.04千元的家庭频率为
P(X>15.04)=P(X>μ+σ)=1?0.68272≈0.1587 ,
则每户家庭获得的扶持资金 Y 的数学期望
E(Y)=15×0.0228+12×0.1359+8×0.6827+0×0.1587=7.4344≈7.434 千元.
【解析】 (1)先计算频率,再补全图形;
(2)P(μ-σ<X≤μ+σ)=0.6827和P(x<X<2μ-x)=0.6827可知x=μ-σ;
(3)根据正态分布分别计算需要补助的各种家庭所占的比例,再计算数学期望.
第七章随机变量及其分布
17462502178057.5正态分布
7.5正态分布
-101600295910知识点1-----正态分布
知识点1-----正态分布
(1)定义
如果对于任何实数随机变量满足:,则称随机变量服从正态分布。记为
(2)正态分布的期望与方差
若,,则的期望与方差分别为:,。
要点诠释:
(1)正态分布由参数和确定。
参数是均值,它是反映随机变量取值的平均水平的特征数,可用样本的均值去估计。是
标准差,它是衡量随机变量总体波动大小的特征数,可以用样本的标准差去估计。
(2)经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.
在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.
-107950290195知识点2-----正态曲线
知识点2-----正态曲线
1.正态曲线:
沿着横轴方向水平移动只能改变对称轴的位置,曲线的形状没有改变, 所得的曲线依然是正态曲线false函数,其中false,false为参数.
显然对于任意x∈R,false,它的图象在x轴的上方,可以证明x轴和曲线之间的区域的面积为1,我们称false为正态密度函数,称它的图象为正态分布密度曲线,简称正态曲线.若随机变量X的概率密度函数为false,则称随机变量X服从正态分布,记为X~false,特别地,当=0,=1时,称随机变量X服从标准正态分布.
2.正态曲线的性质:
①曲线位于轴上方,与轴不相交;
②曲线是单峰的,它关于直线对称;
③曲线在时达到峰值;
④当时,曲线上升;当时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
⑤曲线与轴之间的面积为1;
⑥决定曲线的位置和对称性;
当一定时,曲线的对称轴位置由确定;如下图所示,曲线随着的变化而沿轴平移。
⑦确定曲线的形状;
当一定时,曲线的形状由确定。越小,曲线越“高瘦”,表示总体的分布越集中;越大,曲线越“矮胖”,表示总体的分布越分散。如下图所示。
要点诠释:
性质①说明了函数具有值域(函数值为正)及函数的渐近线(x轴).性质②并且说明了函数具有对称性;性质③说明了函数在x=时取最值;性质⑦说明越大,总体分布越分散,越小,总体分布越集中.
4762522860 重难点探究
重难点探究
随机变量取值的概率与面积的关系
若随机变量ξ服从正态分布,那么对于任意实数a、b(a<b),当随机变量ξ在区间(a,b]上取值时,其取值的概率与正态曲线与直线x=a,x=b以及x轴所围成的图形的面积相等.如图(1)中的阴影部分的面积就是随机变量孝在区间(a,b]上取值的概率.
一般地,当随机变量在区间(-∞,a)上取值时,其取值的概率是正态曲线在x=a左侧以及x轴围成图形的面积,如图(2).随机变量在(a,+∞)上取值的概率是正态曲线在x=a右侧以及x轴围成图形的面积,如图(3).
根据以上概率与面积的关系,在有关概率的计算中,可借助与面积的关系进行求解.
正态分布在三个特殊区间的概率值:
;
;
。
上述结果可用下图表示:
要点诠释:
若随机变量服从正态分布,则落在内的概率约为,落在之外的概率约为,一般称后者为小概率事件,并认为在一次试验中,小概率事件几乎不可能发生。
一般的,服从于正态分布的随机变量通常只取之间的值,简称为原则。
求正态分布在给定区间上的概率方法
(1)数形结合,利用正态曲线的对称性及曲线与轴之间面积为1。
①正态曲线关于直线对称,与对称的区间上的概率相等。
例如;
②;
③若,则。
(2)利用正态分布在三个特殊区间内取值的概率:
①;
②;
③。
00经典例题
经典例题
例题1.已知随机变量 ξ~N(μ,σ2) ,有下列四个命题:
甲: P(ξ
丙: (ξ≤a)=0.5 ? 丁: P(a<ξ
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
【答案】 D
【解析】由于乙、丙的真假性相同,所以乙、丙都是真命题,故 a=μ ,
根据正态分布的对称性可知:甲: P(ξ<μ?1)>P(ξ>μ+2) 为真命题,所以丁为假命题.
并且, P(μ<ξ<μ+1)>P(μ+1<ξ<μ+2) .
所以假命题的是丁.
故为:D
例题2.某种芯片的良品率 X 服从正态分布 N(0.95,0.012) ,公司对科技改造团队的奖励方案如下:若芯片的良品率不超过 95% ,不予奖励;若芯片的良品率超过 95% 但不超过 96% ,每张芯片奖励 100 元;若芯片的良品率超过 96% ,每张芯片奖励 200 元.则每张芯片获得奖励的数学期望为(??? )元附:随机变量 ξ 服从正态分布 N(μ,σ2) ,则 P(μ?σ<ξ<μ+σ)=0.6826 , P(μ?2σ<ξ<μ+2σ)=0.9544 , P(μ?3σ<ξ<μ+3σ)=0.9974 .
A.?52.28??????????????????????????????????B.?65.87??????????????????????????????????C.?50.13??????????????????????????????????D.?131.74
【答案】 B
【解析】因为 X?N(0.95,0.012) ,得出 μ=0.95 , μ+σ=0.96 ,
所以 P(X≤0.95)=P(X≤μ)=0.5 ,
P(0.95
故答案为:B
例题3.国家发展改革委、住房城乡建设部于2017年发布了《生活垃圾分类制度实施方案》,规定46个重点城市在2020年底实施生活垃圾强制分类,垃圾回收、利用率要达35%以上.截至2019年底,这46个重点城市生活垃圾分类的居民小区覆盖率已经接近70%.某市在实施垃圾分类之前,从本市人口数量在两万人左右的320个社区中随机抽取50个社区,对这50个社区某天产生的垃圾量(单位:吨)进行了调查,得到如下频数分布表,并将人口数量在两万人左右的社区产生的垃圾数量超过28(吨/天)的确定为“超标”社区:
垃圾量 X
[12.5,15.5)
[15.5,18.5)
[18.5,21.5)
[21.5,24.5)
[24.5,27.5)
[27.5,30.5)
[30.5,33.5)
频数
5
6
9
12
8
6
4
附:若随机变量 X 服从正态分布 N(μ,σ2) ,则 P(μ?σ
(2)若该市人口数量在两万人左右的社区一天产生的垃圾量 X 大致服从正态分布 N(μ,σ2) ,其中 μ , σ2 分别近似为(1)中样本的平均值 x ,方差 s2 ,经计算 s 约为5.2.请利用正态分布知识估计这320个社区一天中“超标”社区的个数;
(3)通过研究样本原始数据发现,抽取的50个社区中这一天共有8个“超标”社区,市政府决定对这8个“超标”社区的垃圾来源进行跟踪调查,现计划在这8个“超标”社区中随机抽取5个进行跟踪调查,设 Y 为抽到的这一天产生的垃圾量 至少为30.5吨的社区个数,求 Y 的分布列与数学期望.
【答案】 (1)解:由频数分布表得
x=14×5+17×6+20×9+23×12+26×8+29×6+32×450
=22.76≈22.8 ,
所以这50个社区这一天产生的垃圾量的平均值为22.8吨
(2)解:由(1)知 μ=22.8 .因为 s 约为5.2,所以取 σ=5.2 .
所以 P(X>28)=P(X>μ+σ)
=1?0.68272=0.15865 .
又 320×0.15865=50.768≈51 ,
所以估计这320分社区一天中“超标”社区的个数为51
(3)解:由频数分布表知:8个“超标”社区中这一天产生的垃圾量至少为30.5吨的社区有4个,所以 Y 的可能取值为1,2,3,4,
P(Y=1)=C41C44C85=114 ,
P(Y=2)=C42C43C85=37 ,
P(Y=3)=C43C42C85=37 ,
P(Y=4)=C44C41C85=114 ,
所以 Y 的分布列为
Y
1
2
3
4
P
114
37
37
114
所以 E(Y)=1×114+2×37+3×37+4×114=52
【解析】(1)利用图表中的数据算平均数的方法可以直接计算出来;
(2)根据正态分布的规律,计算公式可以直接计算出结果;
(3)由题意可知Y可以取值1,2,3,4,再由超几何分布概率的计算方法分别计算出对应的概率,即可计算出结果.
?
例题4.标准的医用外科口罩分三层,外层有防水作用,可防止飞来进入口罩里面,中间层有过滤作用,对于直径小于5微米的颗粒阻隔率必须大于90%,近口鼻的内层可以吸湿,根据国家质量监督检验标准,过滤率是重要的参考标准,为了监控某条口罩生产线的生产过程,检验员每天从该生产线上随机抽取10个口罩,并检验过滤率.根据长期生产经验,可以认为这条生产线正常状态下生产的口罩的过滤率 z 服从正态分布 N(μ,σ2) .
(附:若随机变量 X 服从正态分布 N(μ,σ2) ,则① P(μ?σ
(2)下面是检验员在一天内抽取的10个口罩的过滤率:
1
2
3
4
5
6
7
8
9
10
0.9376
0.9121
0.9424
0.9572
0.9518
0.9058
0.9216
0.9171
0.9635
0.9268
经计算得: x=110i=110xi=0.9335 , s=110i=110(xi?x)2≈0.0189 (其中 xi 为抽取的第 i 个口罩的过滤率)用样本平均数 x 作为 μ 的估计值,用样本标准差 s 作为 σ 的估计值,利用该正态分布,求 P(z≥0.9524) (精确到 0.001 )
【答案】 (1)解:已知检验率服从正态分布 N(μ,σ2) ,则事件 P(X<μ?3σ)=1?0.99742=0.0013
当生产状态正常时,重复不放回的取10个口罩属于独立重复事件, n=10 , p=0.0013 ,
故有: E(X)=np=10×0.0013=0.013 ,
而 P(X≥1)=1?P(X=0)=1?C100p0(1?p)10=1?0.998710=0.0129 .
(2)解:由题意知:由平均数近似估计 μ ,
则有 P(z≥0.9524)=P(z≥x+s)=1?0.68262=0.1587 .
【解析】(1)已知可知检验率服从正态分布 N(μ,σ2)? ,通过PX=0可求出 P(X≥1)=1?P(X=0)≈0.0129?,利用二项分布的期望公式计算可得结论;
(2)利用公式即可得到结论。
-5588038100随堂练习
随堂练习
练习1.某校一次高三年级数学检测,经抽样分析,成绩 ξ 占近似服从正态分布 N(95,σ2) ,且 P(91<ξ≤95)=0.25 .若该校有700人参加此次检测,估计该校此次检测数学成绩不低于99分的人数为(??? )
A.?100??????????????????????????????????????B.?125??????????????????????????????????????C.?150??????????????????????????????????????D.?175
练习2.某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数为 f(x)=12π?10e?(x?80)2200(x∈R) ,则下列命题中不正确的是(??? )
A.?分数在110分以上的人数与分数在50分以下的人数相同
B.?该市这次考试的数学平均成绩 μ 为80分
C.?该市这次考试的数学成绩的标准差 σ 为10
D.?可以简记为:数学成绩服从正态分布 N(80,10)
练习3.已知随机变量 X?N(2,1) ,其正态分布密度曲线如图所示,若向长方形 OABC 中随机投掷1点,则该点恰好落在阴影部分的概率为(??? )(附:若随机变量 ξ?N(μ,σ2) ,则 P(μ?σ<ξ≤μ+σ)=0.6826 , P(μ?2σ<ξ≤μ+2σ)=0.9544 .)
A.?0.1359???????????????????????????????B.?0.7282???????????????????????????????C.?0.8641???????????????????????????????D.?0.93205
练习4.某单位招考工作人员,须参加初试和复试,初试通过后组织考生参加复试,共5000人参加复试,复试共三道题,第一题考生答对得3分,答错得0分,后两题考生每答对一道题得5分,答错得0分,答完三道题后的得分之和为考生的复试成绩.
(1)通过分析可以认为考生初试成绩 X 服从正态分布 N(μ,δ2) ,其中 μ=64 , δ2=169 ,试估计初试成绩不低于90分的人数;
(2)已知某考生已通过初试,他在复试中第一题答对的概率为 34 ,后两题答对的概率均为 23 ,且每道题回答正确与否互不影响.记该考生的复试试成绩为 Y ,求 Y 的分布列及数学期望.
附:若随机变量 X 服从正态分布 N(μ,δ2) ,则 P(μ?δ
练习5.《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为 3% 、 7% 、 16% 、 24% 、 24% 、 16% 、 7% 、 3% .选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到 [91,100] 、 [81,90] 、 [71,80] 、 [61,70] 、 [51,60] 、 [41,50] 、 [31,40] 、 [21,30] 八个分数区间,得到考生的等级成绩.某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布 N(60,169) .
(1)求物理原始成绩在区间 (47,86) 的人数;
(2)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间 [61,80] 的人数,求X的分布列和数学期望.
(附:若随机变量 ξ~N(μ,σ2) ,则 P(μ?σ<ξ<μ+σ)=0.682 , P(μ?2σ<ξ<μ+2σ)=0.954 , P(μ?3σ<ξ<μ+3σ)=0.997 )
练习6.“全面小康路上一个也不能少”是习近平总书记向全国人民作出的郑重承诺!是对全面建成小康社会的形象表达,其中一个重要指标,就是到2020年我国现行标准下农村贫困人口全面脱贫.目前,全国还有一些贫困县未摘帽,不少贫困村未出列,建档立卡贫困人口尚未全部脱贫.某市为了制定下一步扶贫战略,统计了全市1000户农村贫困家庭的年纯收入,并绘制了如下频率分布直方图:
(1)若这1000户家庭中,家庭年纯收入不低于5(千元)的家庭,且不超过7(千元)的户数为40户,请补全频率分布图,并求出这1000户家庭的年纯收入的平均值 X (同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为这1000户的家庭年纯收入 X 服从正态分布 N(μ,σ2) ,其中 μ 近似为年纯收入的平均值 X,σ2 近似为样本方差,经计算知 σ2=9.26 ;设该市的脱贫标准为家庭年纯收入为 x 千元(即家庭年纯收入大于 x 千元,则该户家庭实现脱贫,否则未能脱贫),若根据此正态分布估计,这1000户家庭中有841.35户家庭实现脱贫,试求该市的脱贫标准 x ;
(3)若该市为了加大扶贫力度,拟投入一笔资金,帮助未脱贫家庭脱贫,脱贫家庭巩固脱贫成果,真正做到“全面小康路上一个也不能少”,方案如下:对家庭年纯收入不超过5.92千元的家庭每户家庭给予扶持资金15千元,对家庭年纯收入超过5.92千元,但不超过8.96千元的家庭每户家庭给予扶持资金12千元,对家庭年纯收入超过8.96千元,但不超过15.04千元的家庭每户家庭给予扶持资金8千元,对家庭年纯收入超过15.04千元的家庭不予以资金扶持,设 Y 为每户家庭获得的扶持资金,求 E(Y) (结果精确到0.001).
附:若随机变量 X~N(μ,?σ2) ,则 P(μ?σ
150495-262890参考答案
参考答案
练习1【答案】 D
【解析】由题意,成绩 X 近似服从正态分布 N(95,σ2) ,
则正态分布曲线的对称轴为 X=95 ,
又由 P(91<ξ≤95)=0.25 ,
根据正态分布曲线的对称性,可得 P(X≥99)=12×[1?2×P(91
故答案为:D.
练习2【答案】 D
【解析】由 f(x)=12π?10e?(x?80)2200(x∈R) ,可得该正态分布为 N(80,100) ,
所以分数在110分以上的人数与分数在50分以下的人数相同,
该市这次考试的数学平均成绩 μ 为80分,标准差 σ 为10。
故答案为:D
练习3【答案】 D
【解析】解:根据题意,随机变量满足正态分布 X?N(2,1) ,
得 μ=2,σ2=1 ,则对称轴为 x=2 , σ=1 ,
根据正态分布密度曲线的对称性,可得:
P(0≤X≤1)=12[P(0≤X≤4)?P(1≤X≤3)]
即 P(0≤X≤1)=12[P(μ?2σ≤X≤μ+2σ)?P(μ?σ≤X≤μ+σ)]
=12×(0.9544?0.6826)=0.1359 ,
可知长方形 OABC 的面积为: 1×2=2 ,设阴影部分的为 S ,
故所求的概率为 P=S2=2?0.13592=0.93205 .
即向长方形 OABC 中随机投掷1点,则该点恰好落在阴影部分的概率为0.93205.
故答案为:D.
练习4【答案】 (1)解:∵学生笔试成绩 X 服从正态分布 N(μ,δ2) ,其中 μ=64 , δ2=169 ,
μ+2δ=64+2×13=90
∴ P(X≥90)=P(X≥μ+2δ)=12(1?0.9544)=0.0228
∴估计笔试成绩不低于90分的人数为 0.0228×5000=114 人
(2)解: Y 的取值分别为0,3,5,8,10,13,
则 P(Y=0)=(1?34)×(1?23)2=136
P(Y=3)=34×(1?23)2=336=112
P(Y=5)=(1?34)×C21×23×(1?23)=19
P(Y=8)=34×C21×23×(1?23)=39=13
P(Y=10)=(1?34)×(23)2=19
P(Y=13)=34×(23)2=39=13
Y 的分布为
故 ξ 的分布列为:
Y
0
3
5
8
10
13
P
136
112
19
13
19
13
E(Y)=0×136+3×112+5×19+8×13+10×19+13×13=32136=10712
【解析】(1)利用正态分布的数据代入数值计算出结果即可。
(2)首先求出满足题意的Y的取值,然后再求出对应Y的值的概率值,由此得到Y的分布,再把数值代入到数学期望的公式计算出结果即可。
练习5【答案】 (1)解:因为物理原始成绩 ξ?N(60,132) ,
所以 P(47<ξ<86)=P(47<ξ<60)+P(60≤ξ<86)
=12P(60?13<ξ<60+13)+12P(60?2×13≤ξ<60+2×13)
=0.6822+0.9542
=0.818 .
所以物理原始成绩在(47,86)的人数为 2000×0.818=1636 (人).
(2)解:由题意得,随机抽取1人,其成绩在区间[61,80]内的概率为 25 .
所以随机抽取三人,则 X 的所有可能取值为0,1,2,3,且 X?B(3,25) ,
所以 P(X=0)=(35)3=27125 ,
P(X=1)=C31?25?(35)2=54125 ,
P(X=2)=C32?(25)2?35=36125 ,
? P(X=3)=(25)3=8125 .
所以 X 的分布列为
X
0
1
2
3
P
27125
54125
36125
8125
所以数学期望 E(X)=3×25=65 .
【解析】(Ⅰ)根据正态曲线的对称性,可将区间 (47,86) 分为 (47,60) 和 (60,86) 两种情况,然后根据特殊区间上的概率求出成绩在区间 (47,86) 内的概率,进而可求出相应的人数;(Ⅱ)由题意得成绩在区间[61,80]的概率为 25 ,且 X?B(3,25) ,由此可得X的分布列和数学期望.
练习6【答案】 (1)解:家庭年纯收入不低于5(千元)且不超过7(千元)的频率为 401000=0.04 ,
纵坐标为0.02;家庭年纯收入超过15(千元),但不超过17(千元)的家庭频率为
1?2×(0.02+0.05+0.12+0.16+0.06+0.04)=0.1 ,纵坐标为0.05,
补全频率分布直方图如下图:
这1000户家庭的年纯收入的平均值为: 6×0.04+8×0.1+10×0.24+12×0.32+14×0.12+16×0.1+18×0.08=12 .
(2)解:1000户家庭中有841.35户家庭实现脱贫,
则未脱贫概率为 1?841.351000=0.15865 ,
设该市的脱贫标准为 x ,则 P(x
(3)解: ∵μ=12,σ=9.26=3.04,∴μ?2σ=5.92 ,
μ?σ=8.96,μ+σ=15.04 ,
家庭年纯收入不超过5.92千元的家庭频率为
P(X<5.92)=P(X<μ?2σ)=1?0.95452≈0.0228 ,
家庭年纯收入超过5.92千元,但不超过8.96千元的家庭频率为
P(5.92
P(8.96
P(X>15.04)=P(X>μ+σ)=1?0.68272≈0.1587 ,
则每户家庭获得的扶持资金 Y 的数学期望
E(Y)=15×0.0228+12×0.1359+8×0.6827+0×0.1587=7.4344≈7.434 千元.
【解析】 (1)先计算频率,再补全图形;
(2)P(μ-σ<X≤μ+σ)=0.6827和P(x<X<2μ-x)=0.6827可知x=μ-σ;
(3)根据正态分布分别计算需要补助的各种家庭所占的比例,再计算数学期望.
