第6章计数原理综合复习-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案)
文档属性
| 名称 | 第6章计数原理综合复习-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册讲义(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 164.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览



文档简介
1130300012306300第六章计数原理
343662025400 综合复习
综合复习
知识点1-----分类加法计数原理
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
知识点2-----分步乘法计数原理
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
86995113665 知识点3-----使用分步乘法计数原理计数的两个注意点
知识点3-----使用分步乘法计数原理计数的两个注意点
1.注意点
一是:要按照事件发生的过程合理分步,即分步是有先后顺序的;
二是:各步中的方法互相依存,缺一不可,只有各个步骤都完成才算完成这件事.
2.利用分步乘法计数原理计数时的解题流程
知识点4-----排列
排列的定义-----一般地,从n 个不同元素中取出m(m≤n)个元素,并按照一一定的 顺序排成一列, 叫做从n个不同元素中取出m个元素的一个排列
排列数的定义:
从n 个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n 个不同元素中取出m个元素的排列数,用符号false表示
排列数公式:
排列数公式:false=n(n-1)(n-2)...(n-m+1)
(2)全排列:false=n(n-1)(n-2)×...×3×2×1
(3)阶乘:false=n!规定0!=1
(4)排列数的性质:false=nfalse,false=mfalse+false
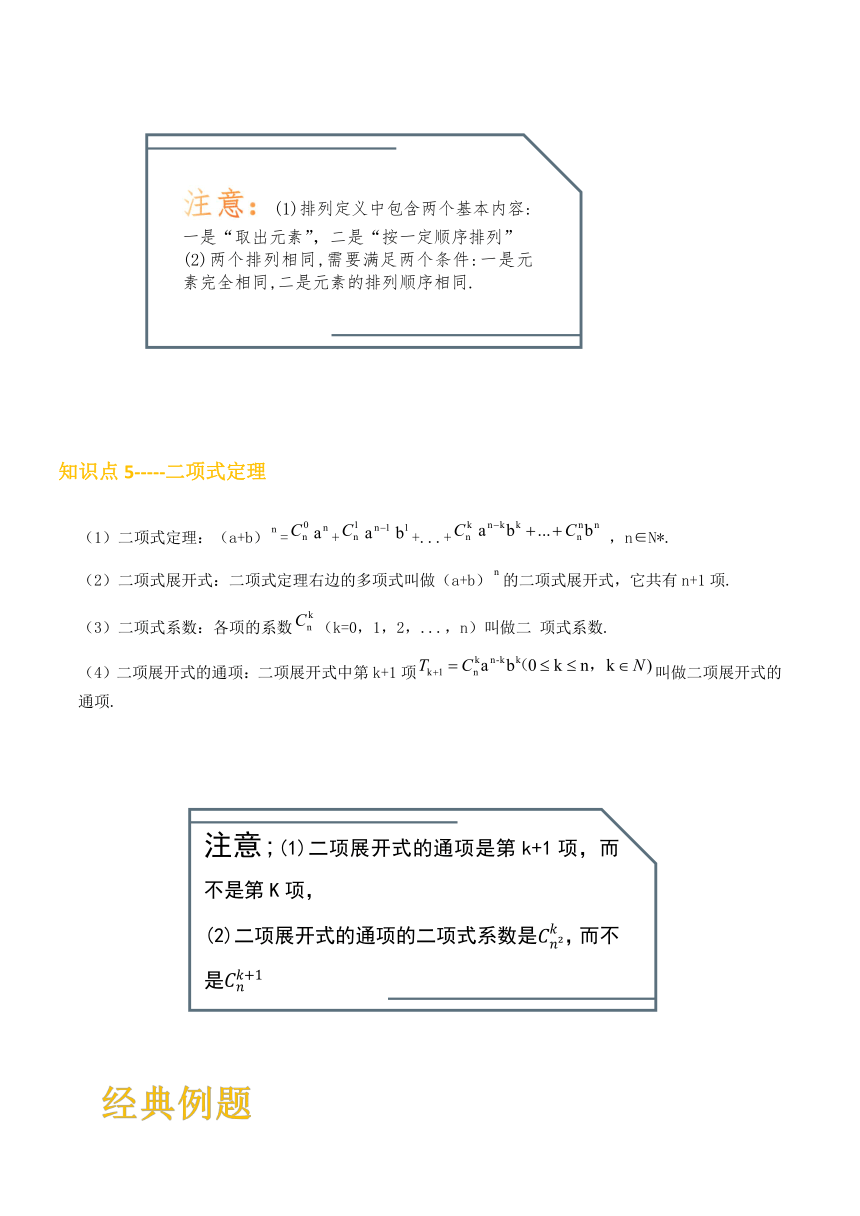
604520-323215注意:(1)排列定义中包含两个基本内容:一是“取出元素”,二是“按一定顺序排列”
(2)两个排列相同,需要满足两个条件:一是元素完全相同,二是元素的排列顺序相同.
注意:(1)排列定义中包含两个基本内容:一是“取出元素”,二是“按一定顺序排列”
(2)两个排列相同,需要满足两个条件:一是元素完全相同,二是元素的排列顺序相同.
-270510404495 知识点5-----二项式定理
知识点5-----二项式定理
9817102636520注意;(1)二项展开式的通项是第k+1项,而不是第K项,
(2)二项展开式的通项的二项式系数是Cn?k,而不是Cnk+1
注意;(1)二项展开式的通项是第k+1项,而不是第K项,
(2)二项展开式的通项的二项式系数是Cn?k,而不是Cnk+1
二项式定理:(a+b)false=falsefalse+falsefalsefalse+...+falsefalse,n∈N*.
(2)二项式展开式:二项式定理右边的多项式叫做(a+b)false的二项式展开式,它共有n+1项.
(3)二项式系数:各项的系数false(k=0,1,2,...,n)叫做二 项式系数.
(4)二项展开式的通项:二项展开式中第k+1项false叫做二项展开式的通项.
111125-80645经典例题
经典例题
例题1.己知 (2x?1)n(n∈N?) 的二项展开式中二项式系数之和为256.
(1)求n的值;
(2)求该展开式中 x3 项的系数.
【答案】 (1)解: 2n=256 ,解得 n=8 ;
(2)解: Tr+1=C8r·(2x)8?r·(?1)r ,令 8?r=3
可得 r=5 时, T6=C85·(2x)3·(?1)3=?448x3 ,
即 x3 项的系数为 ?448 .
【解析】(1)根据题意,由二项式定理可得 2n=256 ,解可得 n=8 ,(2)先求得展开式的通项,可得 r=5 ,将r的值代入通项计算可得答案.
例题2. 7个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
【答案】 (1)解:甲不排头,也不排尾,则甲有5个位置供选择,有5种情况;
将其余6人全排列,安排到其他位置,有 A66 种排法.
共有 5A66=3600 种排法
(2)解:采用捆绑法:先将甲、乙、丙三人看成一个整体,有 A33 种排法,将这个整体与其他四人全排列,有 A33A55=720 种排法
(3)解:先捆绑法:先将甲、乙二人看成一个整体,有 A22 种排法,再将这个整体与丙插入其他四人所形成的空中(包括两端),共有 A44A52 种.
因此,共有 A22A44A52=960 种排法
【解析】(1)利用已知条件结合排列数公式,再结合分步乘法计数原理,进而求出甲不在两端的排法种数。
利用已知条件结合排列数公式,再结合分步乘法计数原理合捆绑法,进而求出甲、乙、丙三个必须在一起的排法种数。
(3)利用已知条件结合排列数公式,再结合分步乘法计数原理合捆绑法,进而求出甲、乙必须在一起,且甲、乙都不能与丙相邻的排法种数。
?
例题3.一场小型晚会有3个唱歌节目和2个相声节目,要求排出一个节目单.
(1)2个相声节目要排在一起,有多少种排法?
(2)第一个节目和最后一个节目都是唱歌节目,有多少种排法?
(3)前3个节目中要有相声节目,有多少种排法?
(要求:每小题都要有过程,且计算结果都用数字表示)
【答案】 (1)解:把两个相声节目捆绑在一起作为一个节目与其他节目排列共有排法 A44A22=48 ;
(2)解:选两个唱歌节目排在首尾,剩下的3个节目在中间排列,排法为 A32A33=36 ;
(3)解:5个节目全排列减去后两个都是相声的排法,共有 A55?A33A22=120?12=108 .
【解析】(1)把两个相声节目捆绑在一起作为一个节目与其他节目排列;(2)选两个唱歌节目排在首尾,还有3个节目在中间排列;(3)5个节目全排列减去后两个都是相声的排法.
例题4.三个女生和五个男生排成一排,
(1)如果女生必须全排在一起,可有多少种不同的排法?
(2)如果女生必须全分开,可有多少种不同的排法?
(3)如果两端都不能排女生,可有多少种不同的排法?
【答案】 (1)解:将女生捆绑在一起当个元素使用,与五个男生共6个元素作全排列,故有 A33?A66 =4320 种;
(2)解:先排五个男生,再将三个女生插进去,故有 A55A63=14400 种;
(3)解:两端先排女生,其余位置随便排,故有 A52A66=14400 种.
【解析】 (1)分捆绑法2步进行分析:①、先把三个女生看成一个整体,考虑其之间的顺序,②将这个整体与五个男生全排列,由分步计数原理计算可得答案;
(2)用插空法分析:①、先把五个男生排好,分析其空位的数目,②、再把三个女生插入这六个位置中,由分步计数原理计算可得答案;
(3)分2步进行分析:①、在5个男生中挑选2个安排在两端,②、将其余6人全排列,安排在其他位置,由分步计数原理计算可得答案.
00随堂练习
随堂练习
练习1 .对于给定的大于1的正整数n,设 x=a0+a1n+a2n2+?+annn ,其中 ai∈{0,1,2,?,n?1},i=0,1,2,?,n ,且 an≠0, 记满足条件的所有x的和为 An ,
(1)求 A2
(2)设 An=nn(n?1)2f(n) ,求 f(n)
练习2.已知 (x+124x)n 的二项展开式中,第三项的系数为7.
(1)求证:前三项系数成等差数列;
(2)求出展开式中所有有理项(即x的指数为整数的项).
练习3.已知(1-2x)7=a0+a1x+a2x2+…+a7x7 , 求:
(1)a1+a2+…+a7;
(2)a1+a3+a5+a7;
(3)a0+a2+a4+a6;
(4)|a0|+|a1|+|a2|+…+|a7|.
练习4.用一颗骰子连掷三次,投掷出的数字顺次排成一个三位数,此时:
(1)各位数字互不相同的三位数有多少个?
(2)可以排出多少个不同的数?
(3)恰好有两个相同数字的三位数共有多少个?
00参考答案
参考答案
练习1【答案】 (1)解:当 n=2 时, x=a0+2a1+4a2 , a0∈{0,1} , a1∈{0,1} , a2=1 ,
故满足条件的 x 共有 4 个,
分别为: x=0+0+4 , x=0+2+4 , x=1+0+4 , x=1+2+4 ,
它们的和是 22.
(2)解:由题意得, a0,a1,a2,?,an?1 各有 n 种取法; an 有 n?1 种取法,
由分步计数原理可得 a0,a1,a2,?,an?1 的不同取法共有 n?n??n?(n?1)=nn(n?1) ,
即满足条件的 x 共有 nn(n?1) 个,
当 a0 分别取 0,1,2,?,n?1 时, a1,a2,?,an?1 各有 n 种取法, an 有 n?1 种取法,
故 An 中所有含 a0 项的和为 (0+1+2+?+n?1)nn?1(n?1)=nn(n?1)22 ;
同理, An 中所有含 a1 项的和为 (0+1+2+?+n?1)nn?1(n?1)?n=nn(n?1)22?n ;
An 中所有含 a2 项的和为 (0+1+2+?+n?1)nn?1(n?1)?n2=nn(n?1)22?n2 ;
An 中所有含 an?1 项的和为 (0+1+2+?+n?1)nn?1(n?1)?nn?1=nn(n?1)22?nn?1 ;
当 an 分别取 i=1,2,?,n?1 时, a0,a1,a2,?,an?1 各有 n 种取法,
故 An 中所有含 an 项的和为 (1+2+?+n?1)nn?nn=nn+1(n?1)2?nn ;
所以 An= nn(n?1)22(1+n+n2+?+nn?1)+nn+1(n?1)2?nn ;
=nn(n?1)22?nn?1n?1+nn+1(n?1)2?nn =nn(n?1)2(nn+1+nn?1)
故 f(n)=nn+1+nn?1 .
【解析】(1)由n=2,直接代入计算得到答案。
(2)将本题看作是分步计数,a 0 , a 1 , a 2 , ? , a n ? 1 各有 n 种取法; a n 有 n ? 1 种取法,计算即得答案。
练习2【答案】 (1)解: T3=Cn2(x)n?2(124x)2=14Cn2xn?32
∵ 14Cn2=7∴Cn2=28∴n(n?1)2=28∴n=8 ,(负值舍去)
所以前三项分别为 T1=C80(x)8(124x)0=x4 , T2=C81(x)7(124x)1=4x134 ,
T3=C82(x)6(124x)2=7x52
所以前三项系数分别为1,4,7, ∵2×4=1+7∴ 前三项系数成等差数列.
(2)解: Tr+1=C8r(x)8?r(124x)r=12rC8rx4?3r4 , r=0,1,2,...,7,8
∴ r=0,4,8 ,展开式中x的指数为整数,
所以展开式中所有有理项为: T1=C80(x)8(12xx)0=x4 、 T4=18C83x=7x 、 T8=1256C88x?2=1256x2 .
【解析】(1)先根据二项展开式通项公式得第三项的系数,再解方程得 n=8 ,最后根据二项展开式通项公式写出前三项系数,根据等差中项性质即可判断;(2)先根据二项展开式通项公式得 x 的指数,再根据 x 的指数为整数确定对应项,即得结果.
练习3【答案】 (1)解:根据所给的等式求得常数项 a0=1 ,令 x=1 ,
∴a0+a1+a2+…+a7=?1
则 a1+a2+…+a7=?2
(2)解:在所给的等式中,令 x=1 ,
可得: a0+a1+a2+…+a7=?1 ???? ①
令 x=?1 ,
则 a0?a1+a2?a3+…?a7=37 ????? ②
用① ? ②再除以 2 可得 a1+a3+a5+a7=?1094
(3)解:用① + ②再除以 2 可得 a0+a2+a4+a6=1093
(4)解:在 (1?2x)7 中,令 x=?1 ,
可得 |a0|+|a1|+|a2|+…+|a7|=a0?a1+a2?a3+…?a7=37=2187
【解析】(1)利用赋值法求出 a1+a2+…+a7 的值。
(2)利用赋值法联立方程组作差再除以2,从而求出 a1+a3+a5+a7 的值。
(3)利用赋值法联立方程组作和再除以2,从而求出 a0+a2+a4+a6 ?的值。
(4)利用赋值法结合去绝对值法,从而求出 |a0|+|a1|+|a2|+…+|a7| 的值。
练习4【答案】 (1)解:得到一个三位数,分三步进行:先填百位,再填十位,最后填个位.百位上的数字填法有6种,十位上的数字填法有5种,个位上的数字填法有4种,根据分步计数原理,各位数字互不相同的三位数有 6×5×4=120 个
(2)解:分三步进行:先填百位,再填十位,最后填各位,每种都有6种方法,根据分步计数原理,可以排出 6×6×6=216 个不同的数.
(3)解:两个数字相同有三种可能性,即第一、二位,第二、三位,第三、一位相同,而每种情况有6×5种,故有3×6×5=90(个).
【解析】(1)得到一个三位数,分三步进行:先填百位,有6种方法;再填十位,有5种方法;最后填个位,有4种方法,根据分步计数原理可得;(2)分三步进行:先填百位,再填十位,最后填个位,每种都有6种方法,根据分步计数原理可得;(3)从三个位中任选两个位,填上相同的数字,有 6C32 种方法,剩下的一位数字的填法有5中,根据分步计数原理可求得结果.
343662025400 综合复习
综合复习
知识点1-----分类加法计数原理
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
任务
分类
完成一件事
有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法
完成这件事共有N种='m+n种不同的方法
计数
知识点2-----分步乘法计数原理
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
任务
分类
完成一件事
需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法
完成这件事共有N种='m×n种不同的方法
计数
86995113665 知识点3-----使用分步乘法计数原理计数的两个注意点
知识点3-----使用分步乘法计数原理计数的两个注意点
1.注意点
一是:要按照事件发生的过程合理分步,即分步是有先后顺序的;
二是:各步中的方法互相依存,缺一不可,只有各个步骤都完成才算完成这件事.
2.利用分步乘法计数原理计数时的解题流程
知识点4-----排列
排列的定义-----一般地,从n 个不同元素中取出m(m≤n)个元素,并按照一一定的 顺序排成一列, 叫做从n个不同元素中取出m个元素的一个排列
排列数的定义:
从n 个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n 个不同元素中取出m个元素的排列数,用符号false表示
排列数公式:
排列数公式:false=n(n-1)(n-2)...(n-m+1)
(2)全排列:false=n(n-1)(n-2)×...×3×2×1
(3)阶乘:false=n!规定0!=1
(4)排列数的性质:false=nfalse,false=mfalse+false
604520-323215注意:(1)排列定义中包含两个基本内容:一是“取出元素”,二是“按一定顺序排列”
(2)两个排列相同,需要满足两个条件:一是元素完全相同,二是元素的排列顺序相同.
注意:(1)排列定义中包含两个基本内容:一是“取出元素”,二是“按一定顺序排列”
(2)两个排列相同,需要满足两个条件:一是元素完全相同,二是元素的排列顺序相同.
-270510404495 知识点5-----二项式定理
知识点5-----二项式定理
9817102636520注意;(1)二项展开式的通项是第k+1项,而不是第K项,
(2)二项展开式的通项的二项式系数是Cn?k,而不是Cnk+1
注意;(1)二项展开式的通项是第k+1项,而不是第K项,
(2)二项展开式的通项的二项式系数是Cn?k,而不是Cnk+1
二项式定理:(a+b)false=falsefalse+falsefalsefalse+...+falsefalse,n∈N*.
(2)二项式展开式:二项式定理右边的多项式叫做(a+b)false的二项式展开式,它共有n+1项.
(3)二项式系数:各项的系数false(k=0,1,2,...,n)叫做二 项式系数.
(4)二项展开式的通项:二项展开式中第k+1项false叫做二项展开式的通项.
111125-80645经典例题
经典例题
例题1.己知 (2x?1)n(n∈N?) 的二项展开式中二项式系数之和为256.
(1)求n的值;
(2)求该展开式中 x3 项的系数.
【答案】 (1)解: 2n=256 ,解得 n=8 ;
(2)解: Tr+1=C8r·(2x)8?r·(?1)r ,令 8?r=3
可得 r=5 时, T6=C85·(2x)3·(?1)3=?448x3 ,
即 x3 项的系数为 ?448 .
【解析】(1)根据题意,由二项式定理可得 2n=256 ,解可得 n=8 ,(2)先求得展开式的通项,可得 r=5 ,将r的值代入通项计算可得答案.
例题2. 7个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
【答案】 (1)解:甲不排头,也不排尾,则甲有5个位置供选择,有5种情况;
将其余6人全排列,安排到其他位置,有 A66 种排法.
共有 5A66=3600 种排法
(2)解:采用捆绑法:先将甲、乙、丙三人看成一个整体,有 A33 种排法,将这个整体与其他四人全排列,有 A33A55=720 种排法
(3)解:先捆绑法:先将甲、乙二人看成一个整体,有 A22 种排法,再将这个整体与丙插入其他四人所形成的空中(包括两端),共有 A44A52 种.
因此,共有 A22A44A52=960 种排法
【解析】(1)利用已知条件结合排列数公式,再结合分步乘法计数原理,进而求出甲不在两端的排法种数。
利用已知条件结合排列数公式,再结合分步乘法计数原理合捆绑法,进而求出甲、乙、丙三个必须在一起的排法种数。
(3)利用已知条件结合排列数公式,再结合分步乘法计数原理合捆绑法,进而求出甲、乙必须在一起,且甲、乙都不能与丙相邻的排法种数。
?
例题3.一场小型晚会有3个唱歌节目和2个相声节目,要求排出一个节目单.
(1)2个相声节目要排在一起,有多少种排法?
(2)第一个节目和最后一个节目都是唱歌节目,有多少种排法?
(3)前3个节目中要有相声节目,有多少种排法?
(要求:每小题都要有过程,且计算结果都用数字表示)
【答案】 (1)解:把两个相声节目捆绑在一起作为一个节目与其他节目排列共有排法 A44A22=48 ;
(2)解:选两个唱歌节目排在首尾,剩下的3个节目在中间排列,排法为 A32A33=36 ;
(3)解:5个节目全排列减去后两个都是相声的排法,共有 A55?A33A22=120?12=108 .
【解析】(1)把两个相声节目捆绑在一起作为一个节目与其他节目排列;(2)选两个唱歌节目排在首尾,还有3个节目在中间排列;(3)5个节目全排列减去后两个都是相声的排法.
例题4.三个女生和五个男生排成一排,
(1)如果女生必须全排在一起,可有多少种不同的排法?
(2)如果女生必须全分开,可有多少种不同的排法?
(3)如果两端都不能排女生,可有多少种不同的排法?
【答案】 (1)解:将女生捆绑在一起当个元素使用,与五个男生共6个元素作全排列,故有 A33?A66 =4320 种;
(2)解:先排五个男生,再将三个女生插进去,故有 A55A63=14400 种;
(3)解:两端先排女生,其余位置随便排,故有 A52A66=14400 种.
【解析】 (1)分捆绑法2步进行分析:①、先把三个女生看成一个整体,考虑其之间的顺序,②将这个整体与五个男生全排列,由分步计数原理计算可得答案;
(2)用插空法分析:①、先把五个男生排好,分析其空位的数目,②、再把三个女生插入这六个位置中,由分步计数原理计算可得答案;
(3)分2步进行分析:①、在5个男生中挑选2个安排在两端,②、将其余6人全排列,安排在其他位置,由分步计数原理计算可得答案.
00随堂练习
随堂练习
练习1 .对于给定的大于1的正整数n,设 x=a0+a1n+a2n2+?+annn ,其中 ai∈{0,1,2,?,n?1},i=0,1,2,?,n ,且 an≠0, 记满足条件的所有x的和为 An ,
(1)求 A2
(2)设 An=nn(n?1)2f(n) ,求 f(n)
练习2.已知 (x+124x)n 的二项展开式中,第三项的系数为7.
(1)求证:前三项系数成等差数列;
(2)求出展开式中所有有理项(即x的指数为整数的项).
练习3.已知(1-2x)7=a0+a1x+a2x2+…+a7x7 , 求:
(1)a1+a2+…+a7;
(2)a1+a3+a5+a7;
(3)a0+a2+a4+a6;
(4)|a0|+|a1|+|a2|+…+|a7|.
练习4.用一颗骰子连掷三次,投掷出的数字顺次排成一个三位数,此时:
(1)各位数字互不相同的三位数有多少个?
(2)可以排出多少个不同的数?
(3)恰好有两个相同数字的三位数共有多少个?
00参考答案
参考答案
练习1【答案】 (1)解:当 n=2 时, x=a0+2a1+4a2 , a0∈{0,1} , a1∈{0,1} , a2=1 ,
故满足条件的 x 共有 4 个,
分别为: x=0+0+4 , x=0+2+4 , x=1+0+4 , x=1+2+4 ,
它们的和是 22.
(2)解:由题意得, a0,a1,a2,?,an?1 各有 n 种取法; an 有 n?1 种取法,
由分步计数原理可得 a0,a1,a2,?,an?1 的不同取法共有 n?n??n?(n?1)=nn(n?1) ,
即满足条件的 x 共有 nn(n?1) 个,
当 a0 分别取 0,1,2,?,n?1 时, a1,a2,?,an?1 各有 n 种取法, an 有 n?1 种取法,
故 An 中所有含 a0 项的和为 (0+1+2+?+n?1)nn?1(n?1)=nn(n?1)22 ;
同理, An 中所有含 a1 项的和为 (0+1+2+?+n?1)nn?1(n?1)?n=nn(n?1)22?n ;
An 中所有含 a2 项的和为 (0+1+2+?+n?1)nn?1(n?1)?n2=nn(n?1)22?n2 ;
An 中所有含 an?1 项的和为 (0+1+2+?+n?1)nn?1(n?1)?nn?1=nn(n?1)22?nn?1 ;
当 an 分别取 i=1,2,?,n?1 时, a0,a1,a2,?,an?1 各有 n 种取法,
故 An 中所有含 an 项的和为 (1+2+?+n?1)nn?nn=nn+1(n?1)2?nn ;
所以 An= nn(n?1)22(1+n+n2+?+nn?1)+nn+1(n?1)2?nn ;
=nn(n?1)22?nn?1n?1+nn+1(n?1)2?nn =nn(n?1)2(nn+1+nn?1)
故 f(n)=nn+1+nn?1 .
【解析】(1)由n=2,直接代入计算得到答案。
(2)将本题看作是分步计数,a 0 , a 1 , a 2 , ? , a n ? 1 各有 n 种取法; a n 有 n ? 1 种取法,计算即得答案。
练习2【答案】 (1)解: T3=Cn2(x)n?2(124x)2=14Cn2xn?32
∵ 14Cn2=7∴Cn2=28∴n(n?1)2=28∴n=8 ,(负值舍去)
所以前三项分别为 T1=C80(x)8(124x)0=x4 , T2=C81(x)7(124x)1=4x134 ,
T3=C82(x)6(124x)2=7x52
所以前三项系数分别为1,4,7, ∵2×4=1+7∴ 前三项系数成等差数列.
(2)解: Tr+1=C8r(x)8?r(124x)r=12rC8rx4?3r4 , r=0,1,2,...,7,8
∴ r=0,4,8 ,展开式中x的指数为整数,
所以展开式中所有有理项为: T1=C80(x)8(12xx)0=x4 、 T4=18C83x=7x 、 T8=1256C88x?2=1256x2 .
【解析】(1)先根据二项展开式通项公式得第三项的系数,再解方程得 n=8 ,最后根据二项展开式通项公式写出前三项系数,根据等差中项性质即可判断;(2)先根据二项展开式通项公式得 x 的指数,再根据 x 的指数为整数确定对应项,即得结果.
练习3【答案】 (1)解:根据所给的等式求得常数项 a0=1 ,令 x=1 ,
∴a0+a1+a2+…+a7=?1
则 a1+a2+…+a7=?2
(2)解:在所给的等式中,令 x=1 ,
可得: a0+a1+a2+…+a7=?1 ???? ①
令 x=?1 ,
则 a0?a1+a2?a3+…?a7=37 ????? ②
用① ? ②再除以 2 可得 a1+a3+a5+a7=?1094
(3)解:用① + ②再除以 2 可得 a0+a2+a4+a6=1093
(4)解:在 (1?2x)7 中,令 x=?1 ,
可得 |a0|+|a1|+|a2|+…+|a7|=a0?a1+a2?a3+…?a7=37=2187
【解析】(1)利用赋值法求出 a1+a2+…+a7 的值。
(2)利用赋值法联立方程组作差再除以2,从而求出 a1+a3+a5+a7 的值。
(3)利用赋值法联立方程组作和再除以2,从而求出 a0+a2+a4+a6 ?的值。
(4)利用赋值法结合去绝对值法,从而求出 |a0|+|a1|+|a2|+…+|a7| 的值。
练习4【答案】 (1)解:得到一个三位数,分三步进行:先填百位,再填十位,最后填个位.百位上的数字填法有6种,十位上的数字填法有5种,个位上的数字填法有4种,根据分步计数原理,各位数字互不相同的三位数有 6×5×4=120 个
(2)解:分三步进行:先填百位,再填十位,最后填各位,每种都有6种方法,根据分步计数原理,可以排出 6×6×6=216 个不同的数.
(3)解:两个数字相同有三种可能性,即第一、二位,第二、三位,第三、一位相同,而每种情况有6×5种,故有3×6×5=90(个).
【解析】(1)得到一个三位数,分三步进行:先填百位,有6种方法;再填十位,有5种方法;最后填个位,有4种方法,根据分步计数原理可得;(2)分三步进行:先填百位,再填十位,最后填个位,每种都有6种方法,根据分步计数原理可得;(3)从三个位中任选两个位,填上相同的数字,有 6C32 种方法,剩下的一位数字的填法有5中,根据分步计数原理可求得结果.
