解直角三角形 新课
图片预览




文档简介
(共20张PPT)
1.回忆三种锐角三角函数的定义
2.复习30°, 45°, 60°角的正弦值,余弦值和正切值
回顾与复习
在美丽的哈尔滨,有著名的亚洲第一高钢塔——龙塔,同学们知道它有多高吗?我们能想办法测量吗?
想 一 想
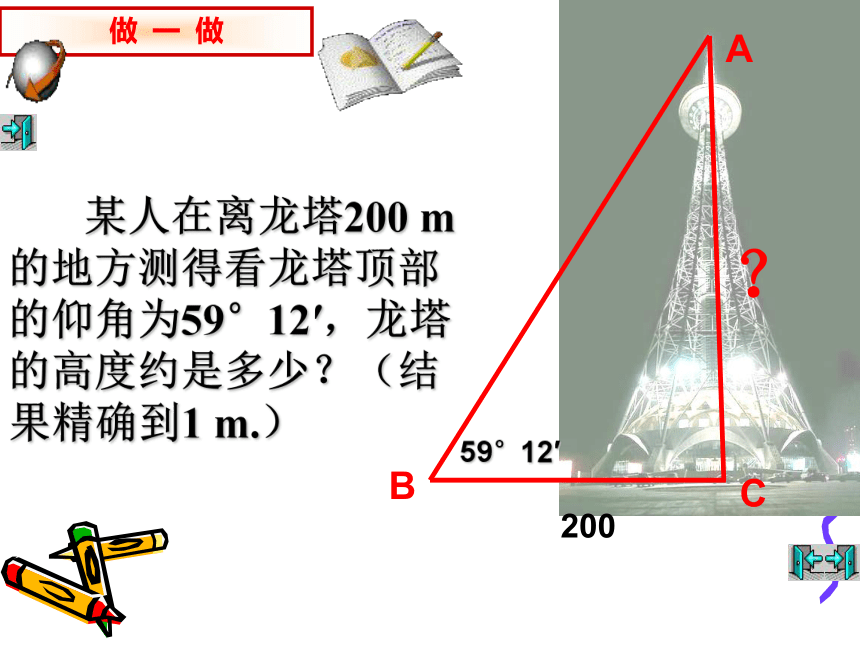
某人在离龙塔200 m的地方测得看龙塔顶部的仰角为59°12′,龙塔的高度约是多少?(结果精确到1 m.)
A
B
C
200
59°12′
?
做 一 做
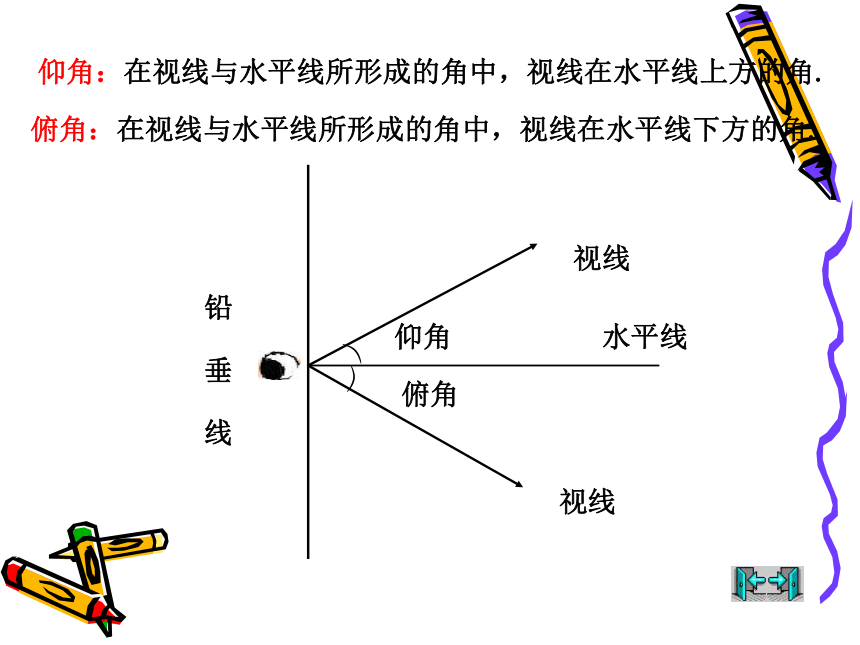
水平线
视线
视线
︶
︶
仰角
俯角
铅 垂 线
仰角:在视线与水平线所形成的角中,视线在水平线上方的角.
俯角:在视线与水平线所形成的角中,视线在水平线下方的角.
A
B
C
200
59°12′
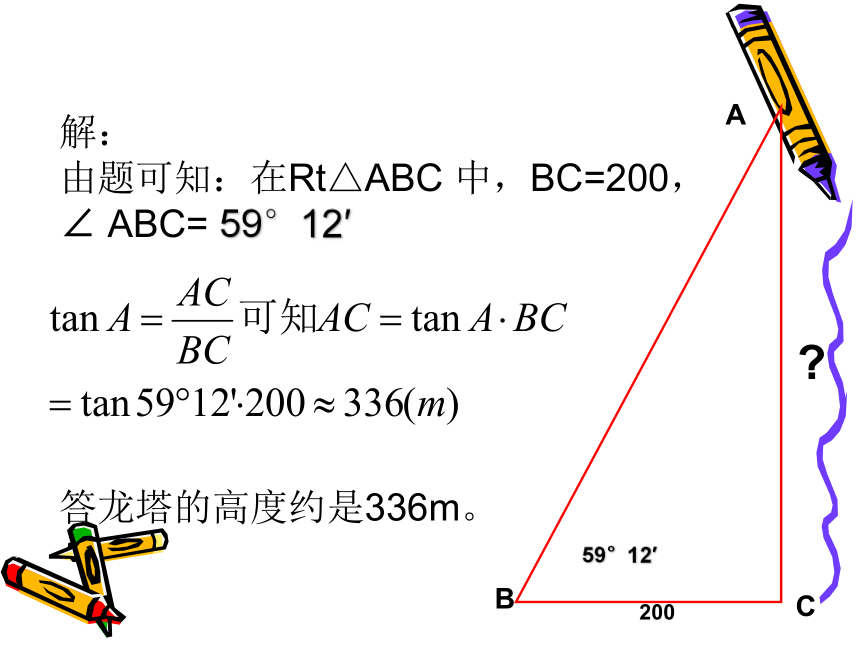
解:
由题可知:在Rt△ABC 中,BC=200,
∠ ABC= 59°12′
答龙塔的高度约是336m。
1.在直角三角形中,除直角外还有几
个元素,它们是什么?
2.在直角三角形中,除直角外的几个
元素之间有哪些关系?
3.知道这几个元素中的几个,就可以
求其余元素?
动 动 脑
2.直角三角形(除直角外)五元素的关系是什么?
(2)锐角之间的关系: ∠A + ∠B = 90°
(1)三边之间的关系: a2 + b2 = c2 (勾股定理)
(3)边角之间的关系 :
A
C
B
a
b
c
3.知道这几个元素中的几个,就可以求其余元素?
思考:
(1)知道一个可以吗?
(2)知道两个呢?
A
B
C
c
a
b
1、已知两个角求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知∠B=30°∠A= 60°求其余的元素。
a=?
b=?
c=?
独立
思考
做不到!
A
B
C
c
a
b
2.已知斜边和一直角边求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知b=4,c=8,求其余元素。
a=
∠A= 60°
∠B= 30°
独立
思考
A
B
C
c
a
b
3.已知斜边和一锐角求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知∠A=45°,c= ,求其余的元素.
∠B= 45°
a=1
b=1
独立
思考
A
B
C
c
a
b
4.已知一直角边和一锐角求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知∠B=30°b=2,求其余的元素。
∠A=30°
a=
c=4
独立
思考
A
B
C
c
a
b
5.已知两直角边求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知a=3,b=3,求其余的元素。
c=
∠A= 45°
∠B=45°
独立
思考
5.已知两直角边求其余的元素可以吗?
4.已知一直角边和一锐角求其余的元素可以吗?
3.已知斜边和一锐角求其余的元素可以吗?
2.已知斜边和一直角边求其余的元素可以吗?
1、已知两个角求其余的元素可以吗?
√
√
√
√
×
A
C
B
a
b
c
类型归纳:
1.已知斜边和一直角边
2.已知斜边和一锐角
3.已知一直角边和一锐角
4.已知两直角边
解直角三角形的定义:
在直角三角形中,由除直角外的已知元素,求出其余未知元素的过程,叫做解直角三角形.
下课了!
试
一
试:
1.回忆三种锐角三角函数的定义
2.复习30°, 45°, 60°角的正弦值,余弦值和正切值
回顾与复习
在美丽的哈尔滨,有著名的亚洲第一高钢塔——龙塔,同学们知道它有多高吗?我们能想办法测量吗?
想 一 想
某人在离龙塔200 m的地方测得看龙塔顶部的仰角为59°12′,龙塔的高度约是多少?(结果精确到1 m.)
A
B
C
200
59°12′
?
做 一 做
水平线
视线
视线
︶
︶
仰角
俯角
铅 垂 线
仰角:在视线与水平线所形成的角中,视线在水平线上方的角.
俯角:在视线与水平线所形成的角中,视线在水平线下方的角.
A
B
C
200
59°12′
解:
由题可知:在Rt△ABC 中,BC=200,
∠ ABC= 59°12′
答龙塔的高度约是336m。
1.在直角三角形中,除直角外还有几
个元素,它们是什么?
2.在直角三角形中,除直角外的几个
元素之间有哪些关系?
3.知道这几个元素中的几个,就可以
求其余元素?
动 动 脑
2.直角三角形(除直角外)五元素的关系是什么?
(2)锐角之间的关系: ∠A + ∠B = 90°
(1)三边之间的关系: a2 + b2 = c2 (勾股定理)
(3)边角之间的关系 :
A
C
B
a
b
c
3.知道这几个元素中的几个,就可以求其余元素?
思考:
(1)知道一个可以吗?
(2)知道两个呢?
A
B
C
c
a
b
1、已知两个角求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知∠B=30°∠A= 60°求其余的元素。
a=?
b=?
c=?
独立
思考
做不到!
A
B
C
c
a
b
2.已知斜边和一直角边求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知b=4,c=8,求其余元素。
a=
∠A= 60°
∠B= 30°
独立
思考
A
B
C
c
a
b
3.已知斜边和一锐角求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知∠A=45°,c= ,求其余的元素.
∠B= 45°
a=1
b=1
独立
思考
A
B
C
c
a
b
4.已知一直角边和一锐角求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知∠B=30°b=2,求其余的元素。
∠A=30°
a=
c=4
独立
思考
A
B
C
c
a
b
5.已知两直角边求其余的元素可以吗?
在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B, ∠C的对边,已知a=3,b=3,求其余的元素。
c=
∠A= 45°
∠B=45°
独立
思考
5.已知两直角边求其余的元素可以吗?
4.已知一直角边和一锐角求其余的元素可以吗?
3.已知斜边和一锐角求其余的元素可以吗?
2.已知斜边和一直角边求其余的元素可以吗?
1、已知两个角求其余的元素可以吗?
√
√
√
√
×
A
C
B
a
b
c
类型归纳:
1.已知斜边和一直角边
2.已知斜边和一锐角
3.已知一直角边和一锐角
4.已知两直角边
解直角三角形的定义:
在直角三角形中,由除直角外的已知元素,求出其余未知元素的过程,叫做解直角三角形.
下课了!
试
一
试:
