18.1勾股定理2
图片预览




文档简介
(共57张PPT)
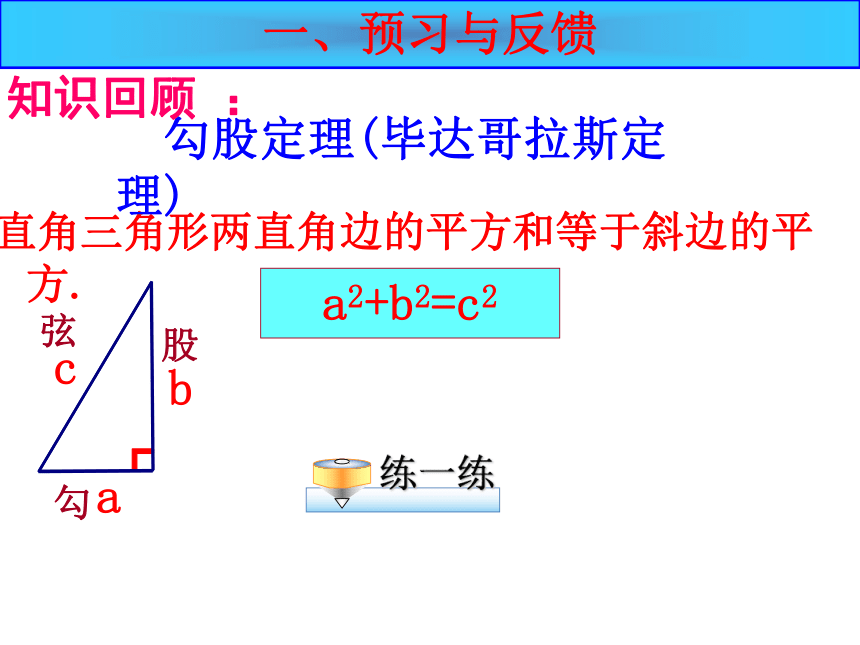
a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方.
┏
a
c
b
勾
股
弦
勾股定理(毕达哥拉斯定理)
一、预习与反馈
知识回顾 :
练一练
例1.在等腰Rt△ABC中, ∠c=90°, a=b=1,则c=
例2.在Rt△ABC中, ∠A=30°, ∠c=90° AB=2,则BC= _
AC=___
1
练一练,想一想
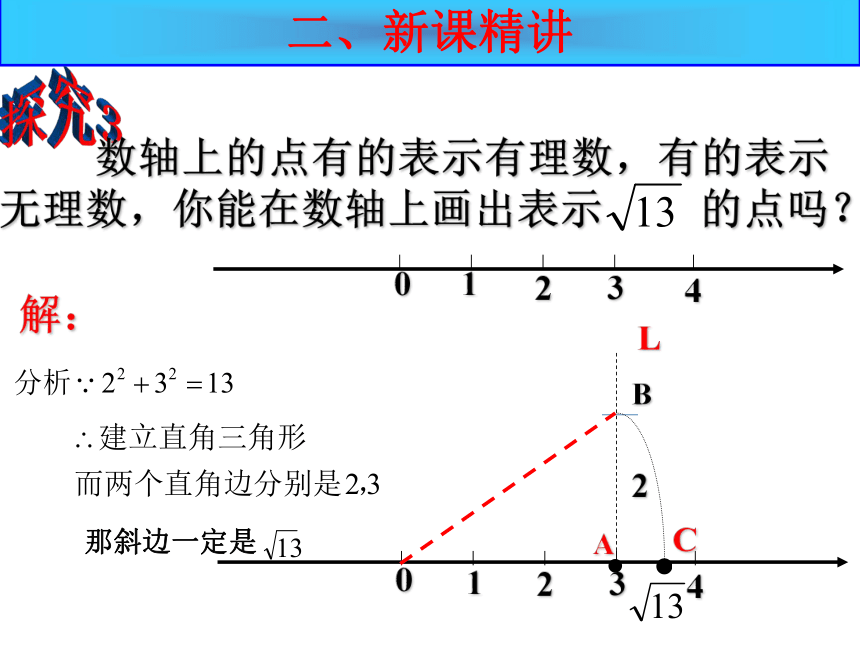
数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的点吗?
0
1
2
3
4
二、新课精讲
0
1
2
3
4
L
A
B
2
C
那斜边一定是
解:
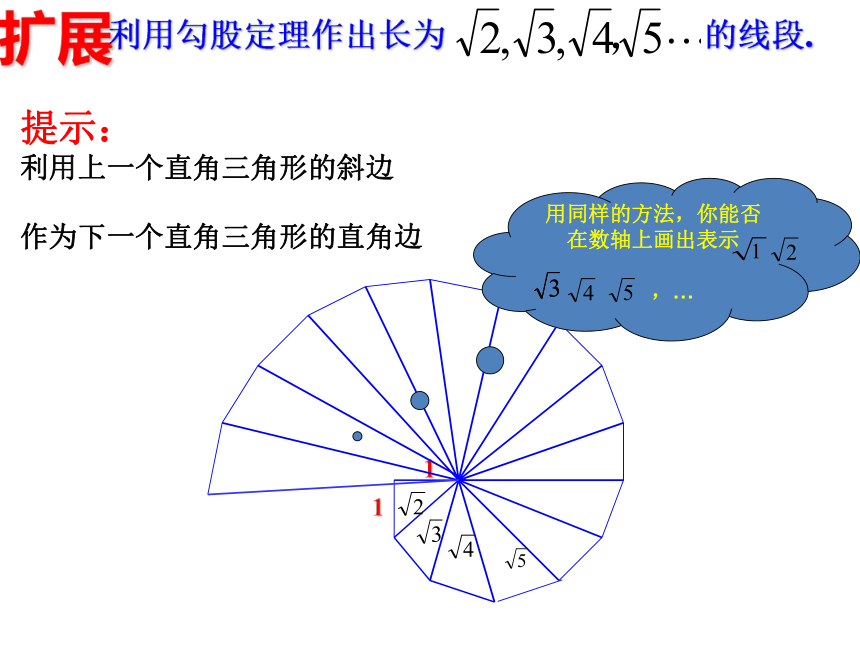
扩展
利用勾股定理作出长为 的线段.
1
1
用同样的方法,你能否在数轴上画出表示
,…
提示:
利用上一个直角三角形的斜边
作为下一个直角三角形的直角边
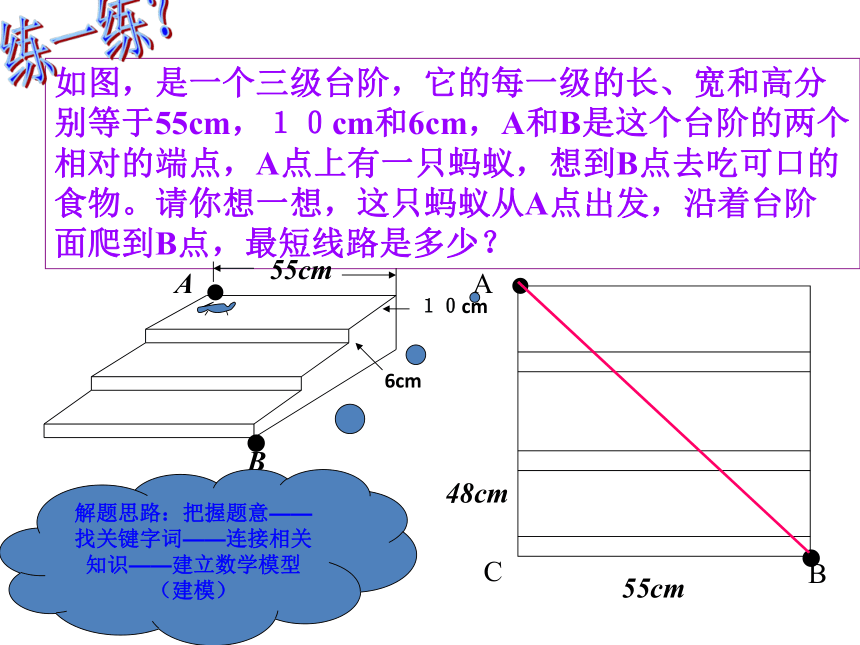
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
55cm
10cm
6cm
55cm
48cm
解题思路:把握题意——找关键字词——连接相关知识——建立数学模型(建模)
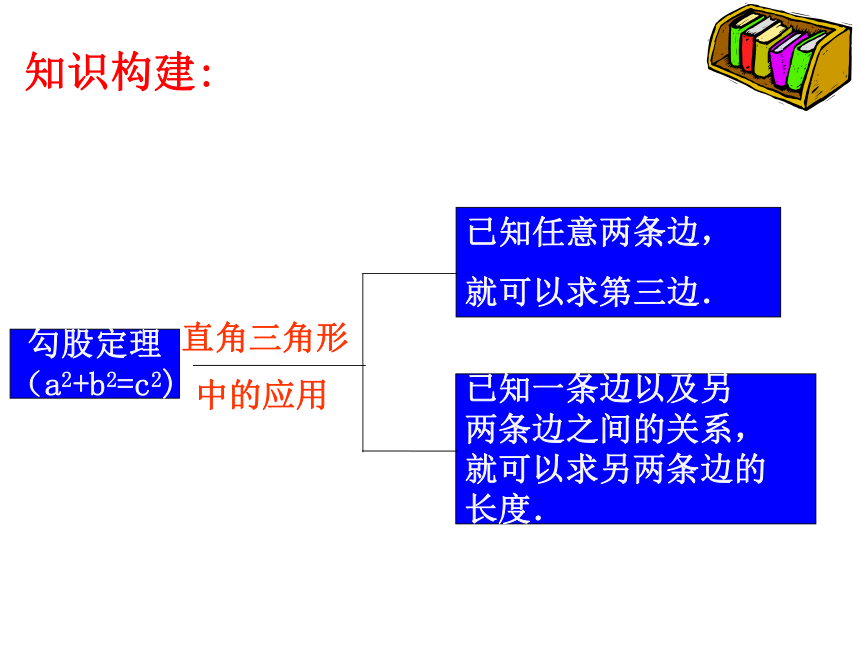
知识构建:
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边以及另
两条边之间的关系,
就可以求另两条边的
长度.
勾股小常识:勾股数
1、 a +b =c ,满足(a,b,c)=1,a,b,c为基本勾股数.
如:3、4、5 ; 5、12、 13; 7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
如:6、8、10; 9、12、15……
3、一组勾股数中必有一个数是5倍数;
4、
练一练
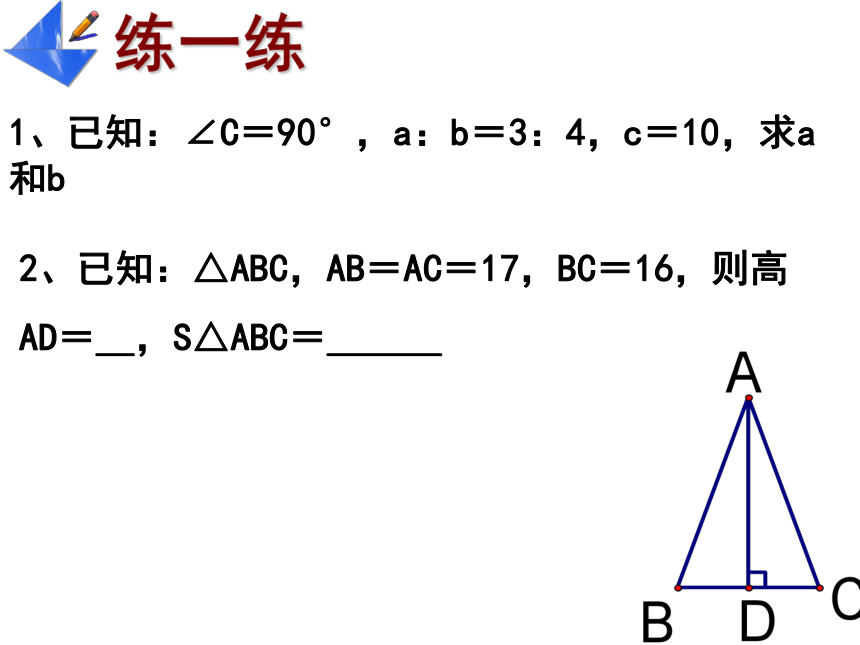
1、已知:∠C=90°,a:b=3:4,c=10,求a和b
2、已知:△ABC,AB=AC=17,BC=16,则高
AD=_,S△ABC=___
3 、 等边三角形的边长为12,则它的高为______
4、在直角三角形中,如果有两边为3,4,那么另一边为_________
5或
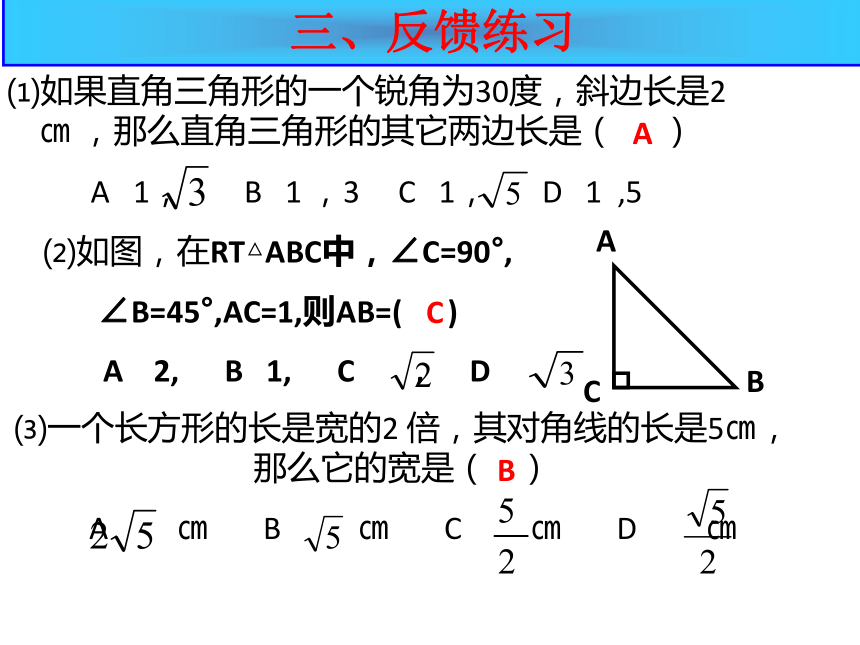
⑶一个长方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
⑴如果直角三角形的一个锐角为30度,斜边长是2 ㎝ ,那么直角三角形的其它两边长是( )
A 1, B 1 ,3 C 1, D 1 ,5
⑵如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2, B 1, C , D
A
C
B
A
B
C
三、反馈练习
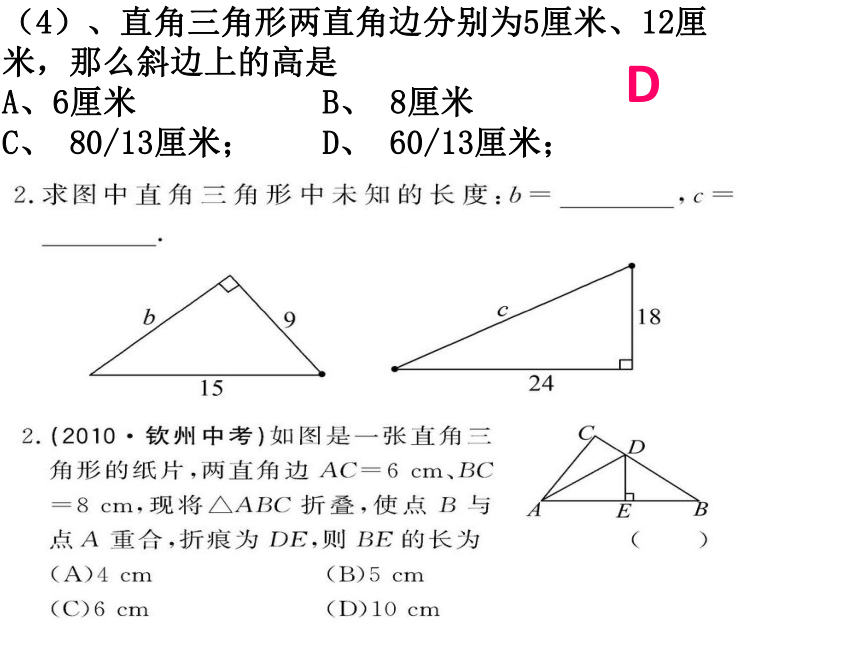
(4)、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
D
【解析】选D.∵∠B=30°,AC⊥AB,AC=5米,所以BC=10米, 米.
大树折断前的高度为AC+BC=15(米).
3.如图所示,一棵大树在一
次强台风中离地面5米处折
断倒下,倒下部分与地面
成30°角,则这棵大树在
折断前的高度和AB的长分
别为( )
(A)10米, 米 (B)15米, 米
(C)10米, 米 (D)15米, 米
5. 已知,在△ABC中,∠A=45°,
AB= +1,则边BC的长为____.
【解析】过点C作CD⊥AB,
∵∠A=45°,∴AD=CD,
∴2AD2=AC2=2,
∴DC=AD=1,
∴BD=AB-AD= +1-1=
在Rt△CDB中,
答案:2
四、小结测试
五、作业
a
c
b
a
b
c
a
b
c
a
b
c
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
对比两个图形,你能直接观察验证出勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
空白部分的面积呢?那剩余的
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
想一想:这四个直角三角形还能怎样拼?
证明一
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
证明三
c2
a2
b2
a2 + b2 = c2
a2
b2
a2
c2
对比两个图形,你能直接观察验证出勾股定理吗?
a
证明六 印度婆什迦羅的證明
c
c2 = b2 + a2
b
证明七 “总统”证法
(a + b)(b + a) = c2 + 2× ab
a2 + 2ab + b2 = c2 +2 ab
a2 + b2 = c2
a
a
b
b
c
c
证明八
证明八
证明八
证明八
证明八
a2
b2
证明九
证明九
证明九
证明九
证明九
c2
a2 + b2 = c2
证明九
证明九
拼图游戏
证明九
拼图游戏
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
证明十
2ab +(b-a)2 = c2
2ab + b2 -2ab + a2 = c2
a2 + b2 = c2
2ab + c2 = (a+b)2
2ab + c2=a2 + b2 + 2ab
a2 + b2 = c2
a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方.
┏
a
c
b
勾
股
弦
勾股定理(毕达哥拉斯定理)
一、预习与反馈
知识回顾 :
练一练
例1.在等腰Rt△ABC中, ∠c=90°, a=b=1,则c=
例2.在Rt△ABC中, ∠A=30°, ∠c=90° AB=2,则BC= _
AC=___
1
练一练,想一想
数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的点吗?
0
1
2
3
4
二、新课精讲
0
1
2
3
4
L
A
B
2
C
那斜边一定是
解:
扩展
利用勾股定理作出长为 的线段.
1
1
用同样的方法,你能否在数轴上画出表示
,…
提示:
利用上一个直角三角形的斜边
作为下一个直角三角形的直角边
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
55cm
10cm
6cm
55cm
48cm
解题思路:把握题意——找关键字词——连接相关知识——建立数学模型(建模)
知识构建:
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边以及另
两条边之间的关系,
就可以求另两条边的
长度.
勾股小常识:勾股数
1、 a +b =c ,满足(a,b,c)=1,a,b,c为基本勾股数.
如:3、4、5 ; 5、12、 13; 7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
如:6、8、10; 9、12、15……
3、一组勾股数中必有一个数是5倍数;
4、
练一练
1、已知:∠C=90°,a:b=3:4,c=10,求a和b
2、已知:△ABC,AB=AC=17,BC=16,则高
AD=_,S△ABC=___
3 、 等边三角形的边长为12,则它的高为______
4、在直角三角形中,如果有两边为3,4,那么另一边为_________
5或
⑶一个长方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
⑴如果直角三角形的一个锐角为30度,斜边长是2 ㎝ ,那么直角三角形的其它两边长是( )
A 1, B 1 ,3 C 1, D 1 ,5
⑵如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2, B 1, C , D
A
C
B
A
B
C
三、反馈练习
(4)、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
D
【解析】选D.∵∠B=30°,AC⊥AB,AC=5米,所以BC=10米, 米.
大树折断前的高度为AC+BC=15(米).
3.如图所示,一棵大树在一
次强台风中离地面5米处折
断倒下,倒下部分与地面
成30°角,则这棵大树在
折断前的高度和AB的长分
别为( )
(A)10米, 米 (B)15米, 米
(C)10米, 米 (D)15米, 米
5. 已知,在△ABC中,∠A=45°,
AB= +1,则边BC的长为____.
【解析】过点C作CD⊥AB,
∵∠A=45°,∴AD=CD,
∴2AD2=AC2=2,
∴DC=AD=1,
∴BD=AB-AD= +1-1=
在Rt△CDB中,
答案:2
四、小结测试
五、作业
a
c
b
a
b
c
a
b
c
a
b
c
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
对比两个图形,你能直接观察验证出勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
空白部分的面积呢?那剩余的
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
想一想:这四个直角三角形还能怎样拼?
证明一
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
证明三
c2
a2
b2
a2 + b2 = c2
a2
b2
a2
c2
对比两个图形,你能直接观察验证出勾股定理吗?
a
证明六 印度婆什迦羅的證明
c
c2 = b2 + a2
b
证明七 “总统”证法
(a + b)(b + a) = c2 + 2× ab
a2 + 2ab + b2 = c2 +2 ab
a2 + b2 = c2
a
a
b
b
c
c
证明八
证明八
证明八
证明八
证明八
a2
b2
证明九
证明九
证明九
证明九
证明九
c2
a2 + b2 = c2
证明九
证明九
拼图游戏
证明九
拼图游戏
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
证明十
2ab +(b-a)2 = c2
2ab + b2 -2ab + a2 = c2
a2 + b2 = c2
2ab + c2 = (a+b)2
2ab + c2=a2 + b2 + 2ab
a2 + b2 = c2
