深圳市六年级下数学第01讲_圆柱与圆锥(教师版)北师大版(带答案)
文档属性
| 名称 | 深圳市六年级下数学第01讲_圆柱与圆锥(教师版)北师大版(带答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览

文档简介
第01讲_圆柱与圆锥
552450219710·知识图谱·
·
·知识图谱·
·
-1133475224155圆柱的认识
1000000圆柱的认识
628650230505·知识精讲·
·
·知识精讲·
·
一.圆柱的认识
圆柱是生活中比较常见的一种立体图形。
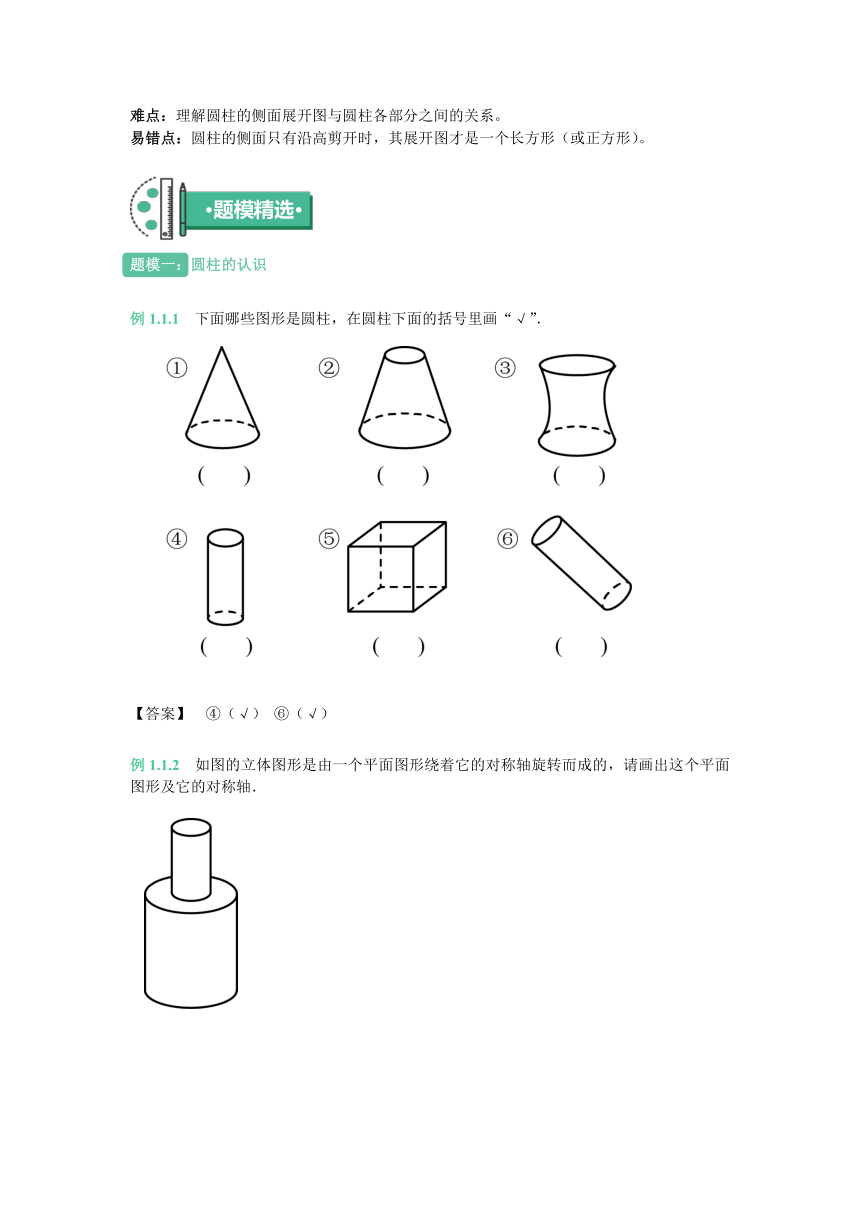
二.圆柱的各部分名称及其特征(如下左图)
1.圆柱是由两个底面和一个侧面围成的。
2.圆柱的两个底面都是圆,并且大小相同;圆柱的侧面是曲面;一个圆柱有无数条高。
??????????????????
三.圆柱的侧面展开图及其与底面之间的关系(如上右图)
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长(或边长)等于圆柱的底面圆周长。宽(或边长)等于圆柱的高。
?
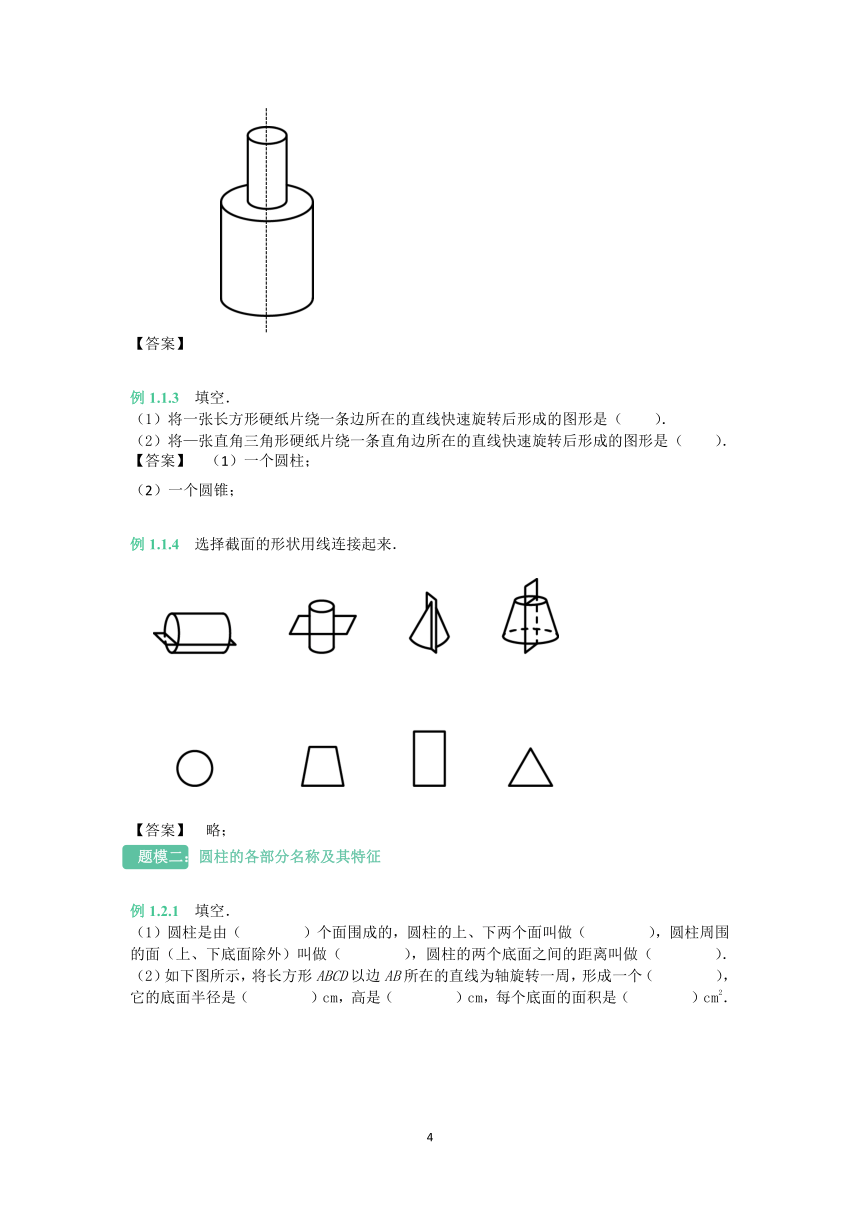
典型例题? 选择哪些材料恰好能做成圆柱形的盒子?
?
名师学堂? 解题思路.圆柱的侧面沿高剪开的展开图是一个长方形或正方形,这个长方形的长(或宽)或正方形的边长等于圆柱的底面周长,所以只要每组两个等圆中的一个圆的周长等于长方形的长(或宽)或正方形的边长,那么这组圆就能和这个长方形或正方形做成圆柱形的盒子。计算对比:(cm),(cm),(cm),因此①和B、②和A或②和C都能做成圆柱形的盒子。
正确答案.选择①和B、②和A或②和C都恰好能做成圆柱形的盒子。
464820188595·三点剖析·
·
·三点剖析·
·
重点:掌握圆柱的特征。
难点:理解圆柱的侧面展开图与圆柱各部分之间的关系。
易错点:圆柱的侧面只有沿高剪开时,其展开图才是一个长方形(或正方形)。
56070577470·题模精选·
·
·题模精选·
·
-67310-15240题模一:圆柱的认识
例1.1.1 下面哪些图形是圆柱,在圆柱下面的括号里画“√”.
【答案】 ④(√) ⑥(√)
例1.1.2 如图的立体图形是由一个平面图形绕着它的对称轴旋转而成的,请画出这个平面图形及它的对称轴.
【答案】
例1.1.3 填空.
(1)将一张长方形硬纸片绕一条边所在的直线快速旋转后形成的图形是( ).
(2)将—张直角三角形硬纸片绕一条直角边所在的直线快速旋转后形成的图形是( ).
【答案】 (1)一个圆柱;
(2)一个圆锥;
例1.1.4 选择截面的形状用线连接起来.
【答案】 略;
-67310-15240 题模二:圆柱的各部分名称及其特征
例1.2.1 填空.
(1)圆柱是由( )个面围成的,圆柱的上、下两个面叫做( ),圆柱周围的面(上、下底面除外)叫做( ),圆柱的两个底面之间的距离叫做( ).
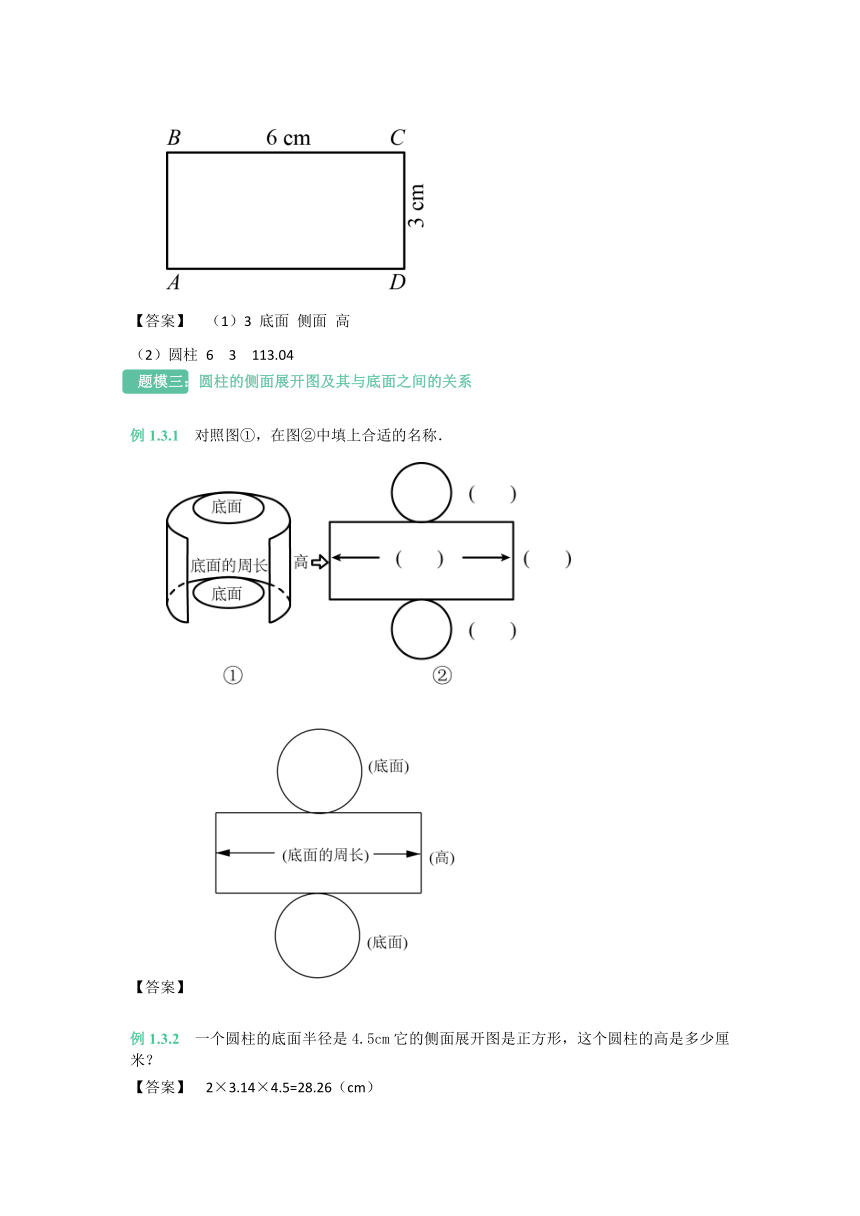
(2)如下图所示,将长方形ABCD以边AB所在的直线为轴旋转一周,形成一个( ),它的底面半径是( )cm,高是( )cm,每个底面的面积是( )cm2.
【答案】 (1)3 底面 侧面 高
(2)圆柱 6 3 113.04
-67310-15240 题模三:圆柱的侧面展开图及其与底面之间的关系
例1.3.1 对照图①,在图②中填上合适的名称.
【答案】
例1.3.2 一个圆柱的底面半径是4.5cm它的侧面展开图是正方形,这个圆柱的高是多少厘米?
【答案】 2×3.14×4.5=28.26(cm)
例1.3.3 圆柱的底面直径是3cm,高是9.42cm,将侧面沿高剪开后是一个正方形.( )
【答案】 √
例1.3.4 一张正方形纸卷成一个圆柱,求这个圆柱的高与底面直径的比.
【答案】 false
523240191135·随堂练习·
·
·随堂练习·
·
随练1.1 请你在圆柱的下面画“√”,不是圆柱的画“×”.
【答案】 略
随练1.2 如图,切完后的截面分别是什么形状?连一连.
【答案】 略
随练1.3 上面一排图形旋转后会得到下面的哪个图形?想一想,连一连.
【答案】 603885118872027984451240155169354512401556038851137920
随练1.4 填一填.
(1)圆柱的侧面展开后是一个( )形.当圆柱的侧面展开后是一个正方形时,这个圆柱的( )与高相等.
(2)一个长方体,最多有( )个面是长方形(不含正方形),最少有( )个面是长方形.
(3)从一个方向观察物体,一次最多只能看到( )个面.
【答案】 (1)长方;底面周长(2)6;4(3)3
随练1.5 填一填.
(1)圆柱的两个底面之间的距离叫做圆柱的( ).
(2)把图1“底面”“底面的周长”“高”分别填入图2的圆柱侧面展开图中的合适位置.
(3)圆柱上下两个底面都是( )形,而且大小( ).把圆柱的侧面沿着高展开,会得到一个( ),圆柱的底面周长等于这个图形的( ),圆柱的高等于这个图形的( ).当圆柱的底面周长和高相等时,沿着高把圆柱的侧面展开得到的是( ).
(4)一个圆柱形玩具,侧面贴着装饰布,圆柱底面半径是10cm,高是18cm.这个装饰布展开后是一个长方形,它的长是( )cm,宽是( )cm.
【答案】 (1)高
(2)略
(3)圆相等长方形长宽正方形
(4)62.8 18
随练1.6 一个圆柱的底面周长是9.42cm,高是6cm,如果沿着这个圆柱的底面直径把它切割成两个半圆柱,切割面的面积一共是多少平方厘米?
【答案】 9.42÷3.14×6×2=36(cm2) 点拨:沿直径切开的切割面是长方形,长方形的一边长是圆柱的直径,切开后切割面是两个这样的长方形.
随练1.7 一个圆柱的侧面展开图是一个长18.84dm,宽9.42dm的长方形,这个圆柱的底面半径是多少分米?
【答案】 18.84÷3.14÷2=3(dm)或9.42÷3.14÷2=1.5(dm)
随练1.8 下面哪个是圆柱的展开图?说说理由.(单位:cm)
【答案】 ②是圆柱的展开图,因为底面周长3×3.14=9.42(cm)正好是长方形的长.
①和③都不是.
随练1.9 下面的长方形绕一条边所在的直线旋转一周后得到的圆柱的底面直径和高各是多少厘米?
【答案】 以一条宽边所在的直线为轴旋转:
底面直径为3×2=6(cm),高为2cm;
以一条长边所在的直线为轴旋转:
底面直径为2×2=4(cm),高为3cm;
随练1.10 用一块长28.26cm,宽15.7cm的长方形铁皮,配上圆形铁皮的直径为( )时,可以做成容积最大的圆柱.
A. 4.5cm
B. 9cm
C. 5cm
D. 2.5cm
【答案】B
点拨:底面周长是28.26cm时,做成最大容积的圆柱.
-1133475224155圆锥的认识
1000000圆锥的认识
628650230505·知识精讲·
·
·知识精讲·
·
一.圆锥的初步认识
圆锥是一种立体图形,生活中有很多物体的形状都是圆锥形的.
二.圆锥各部分的名称和特征
1.圆锥的底面是一个圆,侧面是一个曲面(扇形).
2.圆锥只有一条高.
?
典型例题? 下图是一个圆锥形学具,在透明的玻璃方桌上,从哪个角度观察这个学具可以得到下面的图一、图二和图三?
?
名师学堂? 解题思路.从三个方向观察,列表如下:
观察方向
观察到的形状
对应的图形
圆锥上面
看到圆锥的顶点及圆
图三
圆锥底面
看到圆锥底面的圆
图一
圆锥侧面
看到一个等腰三角形
图二
正确答案.从底面观察,可以得到图一;从侧面观察,可以得到图二;从上面观察,可以得到图三.
464820188595·三点剖析·
·
·三点剖析·
·
重点:圆锥的特征.
难点:圆锥的高的测量方法.
易错点:半圆能围成圆锥,但是整圆不能围成圆锥.
56070577470·题模精选·
·
·题模精选·
·
-67310-15240题模一:圆锥的初步认识
例2.1.1 小法官,巧判断.(下列图形中是圆锥的画“√”,不是圆锥的画“×”)
(1)
(2)
(3)
【答案】 (1)×(2)√(3)√
例2.1.2 转一转,想一想会产生哪种立体图形,用线连一连.
【答案】
例2.1.3 折一折,想一想,能得到什么图形,把下面所对应图形的编号写在括号里.
【答案】 ①②⑤④③⑥
-67310-15240 题模二:圆锥各部分的名称和特征
例2.2.1 填空.
(1)圆锥的底面是个( ),圆锥的侧面是一个( )面.从圆锥的( )到( )的距离是圆锥的高.
(2)圆锥的侧面展开图是一个( ).
(3)把一个圆锥沿底面直径纵向切开平均分成两份,切面是一个( )形.
【答案】 (1)圆 曲 顶点 底面圆心
(2)扇形
(3)等腰三角
例2.2.2 “圆锥和圆柱一样也有无数条高”这句话对吗?为什么?
【答案】 不对,因为圆锥只有一个顶点,只有一条高.
例2.2.3 将下图直角三角形以它的一条直角边所在直线为轴旋转一周,可以得到一个什么图形?所得的图形的底面直径和高各是多少厘米?
【答案】 得到的是圆锥.
(1)以6cm长的边所在直线为旋转轴时,d=16cm,h=6cm
(2)以8cm长的边所在直线为旋转轴时,d=12cm,h=8cm
例2.2.4 下面四种测量圆锥高的方法,你认为( )正确.
A. A选项
B. B选项
C. C选项
D. D选项
【答案】C
523240191135·随堂练习·
·
·随堂练习·
·
随练2.1 连一连.(上面一排图形旋转后是下面的哪个立体图形)
【答案】 59944010934702849880109347014185901093470213360010223501370965974725535940974090
随练2.2 写出下列图形各部分的名称.
【答案】 略
随练2.3 判断.(对的画“√”,错的画“×”)
(1)长方体的每个面一定都是长方形.( )
(2)4个一样的小正方体可以拼成一个大正方体.( )
(3)从圆锥的顶点向底面作垂直切割,得到的截面是等腰三角形.( )
【答案】 (1)×(2)×(3)√
随练2.4 将一个底面直径是36cm,高是9cm的圆锥形木块沿着高分成两个完全相同的木块,表面积比原来增加多少平方厘米?
【答案】 36×9÷2×2=324(cm2)
答:表面积比原来增加324cm2
点拨:切面有两个,它们是两个完全相同的等腰三角形,它们的底是36cm,高是9cm.
随练2.5 一个圆锥的底面半径是3cm,高是4cm,沿着圆锥的高把它切成两半,得到的两个切面是什么形状?一个切面的面积是多少?
【答案】 得到的两个切面是等腰三角形.
(3×2)×4÷2=12(cm2)
答:一个切面的面积是12cm2.
497840170815·能力拓展·
·
·能力拓展·
·
拓展1 填一填.
(1)点动成( ).
线动成( ).面动成( ).
点动成( ).
线动成( ).面动成( ).
(2)在下面各图中,是圆柱的在括号里画“○”,是圆锥的在括号里画“△”.
(3)请标出圆柱和圆锥各部分的名称.
(4)下图中,圆柱高( )cm,圆锥高( )cm.
【答案】 (1)线,面,体(2)略(3)略(4)4,4
拓展2 下面的物体既能嵌入甲图中的空洞,又能嵌入乙图中的空洞的是( ).
A. A选项
B. B选项
C. C选项
D. D选项
【答案】B
拓展3 观察并想象,上面一排图形快速旋转后会得到下面的哪个图形?连一连.
【答案】
拓展4 给下面圆柱的各部分填上相应的名称.
【答案】
拓展5 填一填.
(1)给下面圆柱的各部分填上相应的名称.
(2)折一折,看得到什么图形,填在括号里.
(3)转动长方形ABCD,生成下面的两个圆柱.
圆柱A是以长方形的( )边为轴旋转而成的,底面半径是( ),高是( ).
②圆柱B是以长方形的( )边为轴旋转而成的,底面半径是( ),高是( ).
【答案】 (1)略
(2)圆柱正方体长方体
(3)①AB(或CD) 3cm 1.5cm ②AD(或BC) 1.5cm 3cm
拓展6 认真观察并计算.
图中圆柱一共有( )个面,有( )个侧面和( )个底面.
侧面:_______________________________________________________________________
底面积:_____________________________________________________________________
表面积:_____________________________________________________________________
【答案】 3,1,2
侧面积:4×3.14×6=75.36(cm2)
底面积:(4÷2)2×3.14=12.56(cm2)
表面积:12.56×2+75.36=100.48(cm2)
拓展7 要制作一个无盖的圆柱形水桶,有以下几种型号的铁皮可以选择.(单位:dm)
(1)我选择的材料是( )号和( )号.
(2)我选择的材料制成的水桶的底面直径是( )dm,底面周长是( )dm.高是( )dm.
【答案】 (1)② ③
(2)4 12.56 5
拓展8 选一选.(将正确答案的序号填在括号里)
(1)将绕旗杆旋转一周,得到的立体图形是( ).
(2)把圆柱的侧面展开,得不到图形( ).
(3)下面是圆柱的展开图的是( ).
(4)一个圆柱的侧面展开后是正方形,这个圆柱的( ).
①底面周长和高相等
②底面直径和高相等
③底面半径和高相等
【答案】 (1)②(2)③(3)①(4)①
拓展9 把一个边长是56.52dm的正方形钢板卷成一个最大的圆柱,给这个圆柱配上一个底面,这个底面的面积是多少平方分米?
【答案】 56.52÷3.14÷2=9(dm)
3.14×92=254.34(dm2)
拓展10 下列物体的形状是由哪些图形组成的?
【答案】 略
拓展11 淘气和笑笑爱做游戏,他们做了几面小旗,你能把小旗旋转后形成的图形连起来吗?
【答案】 略
拓展12 填空.
(1)长方体和正方体都有( )个面,( )条棱,( )个顶点.
(2)圆柱体有( )条高,圆锥体有( )条高.
(3)长方体中,最多有( )个面完全相同.
(4)圆柱的侧面沿高展开后是( ),当圆柱的底面周长和高相等时,侧面沿高展开后是( ).
【答案】 (1)6 12 8 (2)无数 1 (3)4 (4)长方形 正方形
拓展13 先填出圆锥各部分的名称,再量出圆锥的底面半径和高.
【答案】
拓展14 如图,以边a所在直线为轴旋转一周,可以得到一个( ),a是它的( ),b是它的( ).
【答案】 圆锥,高,底面半径
拓展15 选一选.(将正确答案的序号填在括号里)
(1)圆锥是由( )个面围成的立体图形.
①1 ②2 ③3
(2)下面测量圆锥的高的方法正确的是( ).
【答案】 (1)②(2)①
552450219710·知识图谱·
·
·知识图谱·
·
-1133475224155圆柱的认识
1000000圆柱的认识
628650230505·知识精讲·
·
·知识精讲·
·
一.圆柱的认识
圆柱是生活中比较常见的一种立体图形。
二.圆柱的各部分名称及其特征(如下左图)
1.圆柱是由两个底面和一个侧面围成的。
2.圆柱的两个底面都是圆,并且大小相同;圆柱的侧面是曲面;一个圆柱有无数条高。
??????????????????
三.圆柱的侧面展开图及其与底面之间的关系(如上右图)
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长(或边长)等于圆柱的底面圆周长。宽(或边长)等于圆柱的高。
?
典型例题? 选择哪些材料恰好能做成圆柱形的盒子?
?
名师学堂? 解题思路.圆柱的侧面沿高剪开的展开图是一个长方形或正方形,这个长方形的长(或宽)或正方形的边长等于圆柱的底面周长,所以只要每组两个等圆中的一个圆的周长等于长方形的长(或宽)或正方形的边长,那么这组圆就能和这个长方形或正方形做成圆柱形的盒子。计算对比:(cm),(cm),(cm),因此①和B、②和A或②和C都能做成圆柱形的盒子。
正确答案.选择①和B、②和A或②和C都恰好能做成圆柱形的盒子。
464820188595·三点剖析·
·
·三点剖析·
·
重点:掌握圆柱的特征。
难点:理解圆柱的侧面展开图与圆柱各部分之间的关系。
易错点:圆柱的侧面只有沿高剪开时,其展开图才是一个长方形(或正方形)。
56070577470·题模精选·
·
·题模精选·
·
-67310-15240题模一:圆柱的认识
例1.1.1 下面哪些图形是圆柱,在圆柱下面的括号里画“√”.
【答案】 ④(√) ⑥(√)
例1.1.2 如图的立体图形是由一个平面图形绕着它的对称轴旋转而成的,请画出这个平面图形及它的对称轴.
【答案】
例1.1.3 填空.
(1)将一张长方形硬纸片绕一条边所在的直线快速旋转后形成的图形是( ).
(2)将—张直角三角形硬纸片绕一条直角边所在的直线快速旋转后形成的图形是( ).
【答案】 (1)一个圆柱;
(2)一个圆锥;
例1.1.4 选择截面的形状用线连接起来.
【答案】 略;
-67310-15240 题模二:圆柱的各部分名称及其特征
例1.2.1 填空.
(1)圆柱是由( )个面围成的,圆柱的上、下两个面叫做( ),圆柱周围的面(上、下底面除外)叫做( ),圆柱的两个底面之间的距离叫做( ).
(2)如下图所示,将长方形ABCD以边AB所在的直线为轴旋转一周,形成一个( ),它的底面半径是( )cm,高是( )cm,每个底面的面积是( )cm2.
【答案】 (1)3 底面 侧面 高
(2)圆柱 6 3 113.04
-67310-15240 题模三:圆柱的侧面展开图及其与底面之间的关系
例1.3.1 对照图①,在图②中填上合适的名称.
【答案】
例1.3.2 一个圆柱的底面半径是4.5cm它的侧面展开图是正方形,这个圆柱的高是多少厘米?
【答案】 2×3.14×4.5=28.26(cm)
例1.3.3 圆柱的底面直径是3cm,高是9.42cm,将侧面沿高剪开后是一个正方形.( )
【答案】 √
例1.3.4 一张正方形纸卷成一个圆柱,求这个圆柱的高与底面直径的比.
【答案】 false
523240191135·随堂练习·
·
·随堂练习·
·
随练1.1 请你在圆柱的下面画“√”,不是圆柱的画“×”.
【答案】 略
随练1.2 如图,切完后的截面分别是什么形状?连一连.
【答案】 略
随练1.3 上面一排图形旋转后会得到下面的哪个图形?想一想,连一连.
【答案】 603885118872027984451240155169354512401556038851137920
随练1.4 填一填.
(1)圆柱的侧面展开后是一个( )形.当圆柱的侧面展开后是一个正方形时,这个圆柱的( )与高相等.
(2)一个长方体,最多有( )个面是长方形(不含正方形),最少有( )个面是长方形.
(3)从一个方向观察物体,一次最多只能看到( )个面.
【答案】 (1)长方;底面周长(2)6;4(3)3
随练1.5 填一填.
(1)圆柱的两个底面之间的距离叫做圆柱的( ).
(2)把图1“底面”“底面的周长”“高”分别填入图2的圆柱侧面展开图中的合适位置.
(3)圆柱上下两个底面都是( )形,而且大小( ).把圆柱的侧面沿着高展开,会得到一个( ),圆柱的底面周长等于这个图形的( ),圆柱的高等于这个图形的( ).当圆柱的底面周长和高相等时,沿着高把圆柱的侧面展开得到的是( ).
(4)一个圆柱形玩具,侧面贴着装饰布,圆柱底面半径是10cm,高是18cm.这个装饰布展开后是一个长方形,它的长是( )cm,宽是( )cm.
【答案】 (1)高
(2)略
(3)圆相等长方形长宽正方形
(4)62.8 18
随练1.6 一个圆柱的底面周长是9.42cm,高是6cm,如果沿着这个圆柱的底面直径把它切割成两个半圆柱,切割面的面积一共是多少平方厘米?
【答案】 9.42÷3.14×6×2=36(cm2) 点拨:沿直径切开的切割面是长方形,长方形的一边长是圆柱的直径,切开后切割面是两个这样的长方形.
随练1.7 一个圆柱的侧面展开图是一个长18.84dm,宽9.42dm的长方形,这个圆柱的底面半径是多少分米?
【答案】 18.84÷3.14÷2=3(dm)或9.42÷3.14÷2=1.5(dm)
随练1.8 下面哪个是圆柱的展开图?说说理由.(单位:cm)
【答案】 ②是圆柱的展开图,因为底面周长3×3.14=9.42(cm)正好是长方形的长.
①和③都不是.
随练1.9 下面的长方形绕一条边所在的直线旋转一周后得到的圆柱的底面直径和高各是多少厘米?
【答案】 以一条宽边所在的直线为轴旋转:
底面直径为3×2=6(cm),高为2cm;
以一条长边所在的直线为轴旋转:
底面直径为2×2=4(cm),高为3cm;
随练1.10 用一块长28.26cm,宽15.7cm的长方形铁皮,配上圆形铁皮的直径为( )时,可以做成容积最大的圆柱.
A. 4.5cm
B. 9cm
C. 5cm
D. 2.5cm
【答案】B
点拨:底面周长是28.26cm时,做成最大容积的圆柱.
-1133475224155圆锥的认识
1000000圆锥的认识
628650230505·知识精讲·
·
·知识精讲·
·
一.圆锥的初步认识
圆锥是一种立体图形,生活中有很多物体的形状都是圆锥形的.
二.圆锥各部分的名称和特征
1.圆锥的底面是一个圆,侧面是一个曲面(扇形).
2.圆锥只有一条高.
?
典型例题? 下图是一个圆锥形学具,在透明的玻璃方桌上,从哪个角度观察这个学具可以得到下面的图一、图二和图三?
?
名师学堂? 解题思路.从三个方向观察,列表如下:
观察方向
观察到的形状
对应的图形
圆锥上面
看到圆锥的顶点及圆
图三
圆锥底面
看到圆锥底面的圆
图一
圆锥侧面
看到一个等腰三角形
图二
正确答案.从底面观察,可以得到图一;从侧面观察,可以得到图二;从上面观察,可以得到图三.
464820188595·三点剖析·
·
·三点剖析·
·
重点:圆锥的特征.
难点:圆锥的高的测量方法.
易错点:半圆能围成圆锥,但是整圆不能围成圆锥.
56070577470·题模精选·
·
·题模精选·
·
-67310-15240题模一:圆锥的初步认识
例2.1.1 小法官,巧判断.(下列图形中是圆锥的画“√”,不是圆锥的画“×”)
(1)
(2)
(3)
【答案】 (1)×(2)√(3)√
例2.1.2 转一转,想一想会产生哪种立体图形,用线连一连.
【答案】
例2.1.3 折一折,想一想,能得到什么图形,把下面所对应图形的编号写在括号里.
【答案】 ①②⑤④③⑥
-67310-15240 题模二:圆锥各部分的名称和特征
例2.2.1 填空.
(1)圆锥的底面是个( ),圆锥的侧面是一个( )面.从圆锥的( )到( )的距离是圆锥的高.
(2)圆锥的侧面展开图是一个( ).
(3)把一个圆锥沿底面直径纵向切开平均分成两份,切面是一个( )形.
【答案】 (1)圆 曲 顶点 底面圆心
(2)扇形
(3)等腰三角
例2.2.2 “圆锥和圆柱一样也有无数条高”这句话对吗?为什么?
【答案】 不对,因为圆锥只有一个顶点,只有一条高.
例2.2.3 将下图直角三角形以它的一条直角边所在直线为轴旋转一周,可以得到一个什么图形?所得的图形的底面直径和高各是多少厘米?
【答案】 得到的是圆锥.
(1)以6cm长的边所在直线为旋转轴时,d=16cm,h=6cm
(2)以8cm长的边所在直线为旋转轴时,d=12cm,h=8cm
例2.2.4 下面四种测量圆锥高的方法,你认为( )正确.
A. A选项
B. B选项
C. C选项
D. D选项
【答案】C
523240191135·随堂练习·
·
·随堂练习·
·
随练2.1 连一连.(上面一排图形旋转后是下面的哪个立体图形)
【答案】 59944010934702849880109347014185901093470213360010223501370965974725535940974090
随练2.2 写出下列图形各部分的名称.
【答案】 略
随练2.3 判断.(对的画“√”,错的画“×”)
(1)长方体的每个面一定都是长方形.( )
(2)4个一样的小正方体可以拼成一个大正方体.( )
(3)从圆锥的顶点向底面作垂直切割,得到的截面是等腰三角形.( )
【答案】 (1)×(2)×(3)√
随练2.4 将一个底面直径是36cm,高是9cm的圆锥形木块沿着高分成两个完全相同的木块,表面积比原来增加多少平方厘米?
【答案】 36×9÷2×2=324(cm2)
答:表面积比原来增加324cm2
点拨:切面有两个,它们是两个完全相同的等腰三角形,它们的底是36cm,高是9cm.
随练2.5 一个圆锥的底面半径是3cm,高是4cm,沿着圆锥的高把它切成两半,得到的两个切面是什么形状?一个切面的面积是多少?
【答案】 得到的两个切面是等腰三角形.
(3×2)×4÷2=12(cm2)
答:一个切面的面积是12cm2.
497840170815·能力拓展·
·
·能力拓展·
·
拓展1 填一填.
(1)点动成( ).
线动成( ).面动成( ).
点动成( ).
线动成( ).面动成( ).
(2)在下面各图中,是圆柱的在括号里画“○”,是圆锥的在括号里画“△”.
(3)请标出圆柱和圆锥各部分的名称.
(4)下图中,圆柱高( )cm,圆锥高( )cm.
【答案】 (1)线,面,体(2)略(3)略(4)4,4
拓展2 下面的物体既能嵌入甲图中的空洞,又能嵌入乙图中的空洞的是( ).
A. A选项
B. B选项
C. C选项
D. D选项
【答案】B
拓展3 观察并想象,上面一排图形快速旋转后会得到下面的哪个图形?连一连.
【答案】
拓展4 给下面圆柱的各部分填上相应的名称.
【答案】
拓展5 填一填.
(1)给下面圆柱的各部分填上相应的名称.
(2)折一折,看得到什么图形,填在括号里.
(3)转动长方形ABCD,生成下面的两个圆柱.
圆柱A是以长方形的( )边为轴旋转而成的,底面半径是( ),高是( ).
②圆柱B是以长方形的( )边为轴旋转而成的,底面半径是( ),高是( ).
【答案】 (1)略
(2)圆柱正方体长方体
(3)①AB(或CD) 3cm 1.5cm ②AD(或BC) 1.5cm 3cm
拓展6 认真观察并计算.
图中圆柱一共有( )个面,有( )个侧面和( )个底面.
侧面:_______________________________________________________________________
底面积:_____________________________________________________________________
表面积:_____________________________________________________________________
【答案】 3,1,2
侧面积:4×3.14×6=75.36(cm2)
底面积:(4÷2)2×3.14=12.56(cm2)
表面积:12.56×2+75.36=100.48(cm2)
拓展7 要制作一个无盖的圆柱形水桶,有以下几种型号的铁皮可以选择.(单位:dm)
(1)我选择的材料是( )号和( )号.
(2)我选择的材料制成的水桶的底面直径是( )dm,底面周长是( )dm.高是( )dm.
【答案】 (1)② ③
(2)4 12.56 5
拓展8 选一选.(将正确答案的序号填在括号里)
(1)将绕旗杆旋转一周,得到的立体图形是( ).
(2)把圆柱的侧面展开,得不到图形( ).
(3)下面是圆柱的展开图的是( ).
(4)一个圆柱的侧面展开后是正方形,这个圆柱的( ).
①底面周长和高相等
②底面直径和高相等
③底面半径和高相等
【答案】 (1)②(2)③(3)①(4)①
拓展9 把一个边长是56.52dm的正方形钢板卷成一个最大的圆柱,给这个圆柱配上一个底面,这个底面的面积是多少平方分米?
【答案】 56.52÷3.14÷2=9(dm)
3.14×92=254.34(dm2)
拓展10 下列物体的形状是由哪些图形组成的?
【答案】 略
拓展11 淘气和笑笑爱做游戏,他们做了几面小旗,你能把小旗旋转后形成的图形连起来吗?
【答案】 略
拓展12 填空.
(1)长方体和正方体都有( )个面,( )条棱,( )个顶点.
(2)圆柱体有( )条高,圆锥体有( )条高.
(3)长方体中,最多有( )个面完全相同.
(4)圆柱的侧面沿高展开后是( ),当圆柱的底面周长和高相等时,侧面沿高展开后是( ).
【答案】 (1)6 12 8 (2)无数 1 (3)4 (4)长方形 正方形
拓展13 先填出圆锥各部分的名称,再量出圆锥的底面半径和高.
【答案】
拓展14 如图,以边a所在直线为轴旋转一周,可以得到一个( ),a是它的( ),b是它的( ).
【答案】 圆锥,高,底面半径
拓展15 选一选.(将正确答案的序号填在括号里)
(1)圆锥是由( )个面围成的立体图形.
①1 ②2 ③3
(2)下面测量圆锥的高的方法正确的是( ).
【答案】 (1)②(2)①
