苏科版 七年级下册 数学课件 8.5小结与思考(共28张)
文档属性
| 名称 | 苏科版 七年级下册 数学课件 8.5小结与思考(共28张) |  | |
| 格式 | ppt | ||
| 文件大小 | 335.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 20:46:41 | ||
图片预览








文档简介
练习八、 计算:
同底数幂的除法
练习十一
(1)a ÷a (2)(-a)÷(-a)
(3)(2a)÷(2a) (4) (-a)÷(-a)
(5)(p )÷p (6)a ÷(-a )
(7)m ÷m ×m (8)(a ) ÷a
练习十二
思考:1、已知210=a2=4b(其中a,b为正整数),求ab的值。
小结:
(1)掌握幂的运算的一些性质及字母的表示方法。
(2)会运用性质完成有关的计算。
(3)注意幂的四种运算的区别。
(4)体会性质的逆运用。
单击此处编辑母版标题样式
*
*
*
单击此处编辑母版副标题样式
第八章 幂的运算
复习目标
1、掌握幂的运算性质。
2、会用语言和公式表述幂的运算的性质。
3、灵活运用幂的运算性质求值。
幂的运算
同底数幂的乘法
同底数幂的除法
积的乘方
幂的乘方
同底数幂的乘法法则:
am·an=am+n
其中m,n都是正整数
语言叙述:
同底数幂相乘,底数不变,指数相加。
字母表示:
学习指导一
幂的乘方法则:
(am)n=amn
其中m,n都是正整数
语言叙述:幂的乘方,底 数不变,指数相乘。
字母表示:
学习指导二
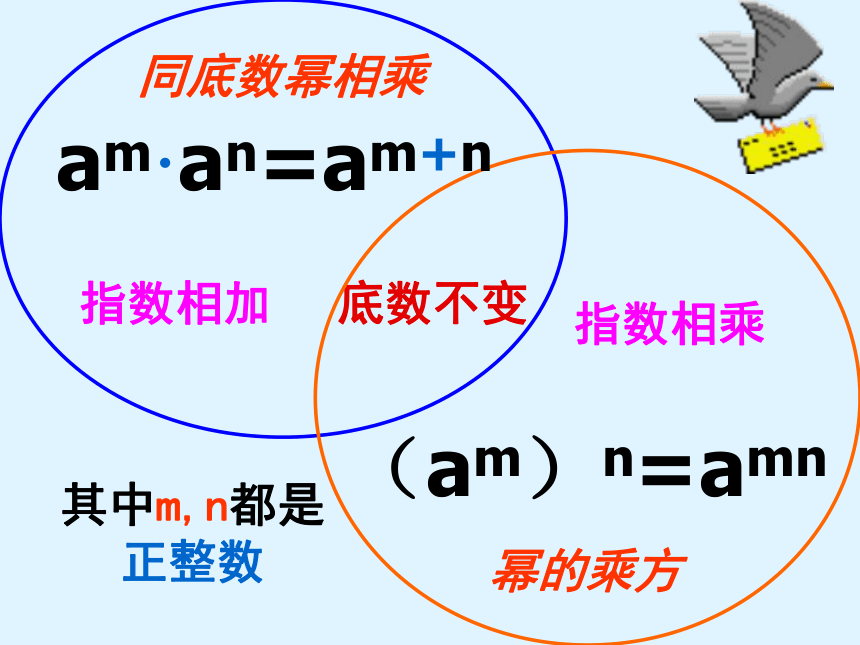
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
(am)n=amn
am·an=am+n
练习一、计算( 口答)
1011
a10
x10
x9
(2) a7 ·a3 =
(3) x5 ·x5 =
(4) x5 ·x ·x3 =
(1) 105×106=
(1)(105)6=
(2)(a7)3 =
(3)(x5)5 =
(4)(y3)2· (y2)3=
1030
a21
x25
y12
y 6 · y 6 =
??练习二、计算( 口答)
102m+1
①10m·10m-1·100=
②3×27×9×3m=
3m+6
练习三、??计算:
③(m-n)4·(m-n) 5·(n-m)6=
④ (x-2y)4·(2y-x) 5·(x-2y)6=
(m-n)15
(2y-x)15
1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x(x5)m (D) xx5xm
c
练习四、选择
2.x14不可以写成( )
(A) x5(x3)3
(B) (-x)(-x2)(-x3)(-x8)
(C) (x7)7
(D) x3x4x5x2
c
3.计算(-32)5-(-35)2的结果是( )
(A)0 (B) -2×310
(C)2×310(D) -2×37
B
2、在xm-1·( )=x2m+1中,括号内应填写的代数式是( )
A、x2m B、x2m+1
C、x2m+2 D、xm+2
D
(1).已知:am=7,bm=4, 求(ab)2m的值。
练习五、??计算:
(2).已知:x+4y-3=0,
求2x●16y的值。
8
练习六:
1、若 am = 2,则a3m =_____.
2、若 mx = 2,my = 3 ,则
mx+y =____,m3x+2y =______.
6
72
m =m m
x
x+y
y
=6
8
动脑筋!
m =(m )? (m )?
3x+2y
x
y
=72
学习指导三
积的乘方的法则:
(ab)m =ambm
其中m是正整数
语言叙述:
积的乘方,等于把积的每一个因式分别乘方,再把所得的积相乘。
字母表示:
(1) (ab) 2 =
(2)(ab)3 =
(3)(ab)4 =
练习七、计算( 口答)
2
2
a
b
3
3
a
b
4
4
a
b
(1)(2b)3
(3)(-a)3
(4)(-3x)4
=23b3
=8b3
=22×(a3)2
=4a6
=(-1)3 ?a3
= -a3
=(-3)4 ? x4
= 81 x4
(2)(2a)3
1.判断下列计算是否正确,并说明理由:
(1)(xy3)2=xy6
(2)(-2x)3=-2x3
x?y6
-8x3
练习九
2.计算:
(1)(3a)2
(2)(-3a)3
(3)(ab2)2
(4)(-2×103)3
=(-3)3a3=-27a3
=a2(b2)2=a2b4
=(-2)3×(103)3=-8×109
=32a2=9a2
(3)-82000×(-0.125)2001
=
=
=
=
(2)(-4)2005×(0.25)2005
=
=
(1)24×44×0.1254
=
=
(2×4×0.125)4
1
(-4×0.25)2005
-1
练习十
-82000×(-0.125)2000× (-0.125)
-82000×0.1252000× (-0.125)
-(8×0.125)2000× (-0.125)
-1× (-0.125) = 0.125
逆 用 法 则 进 行 计 算
学习指导四
字母表示
语言叙述
同底数幂相除,底数不变,指数相减。
a ÷ a =a
m
n
m-n
m 、n为正整数,m>n且a≠0
8
3
10
3
6
4
3
2
5
10
3
2
8
2
3
2
3
4
1、下列算式中,
①a3·a3=2a3;②10×109=1019;③(xy2)3=xy6;④a3n÷an=a3.其中错误的是( )
A、1个 B、2个
C、3个 D、4个
D
_______
,
5
,
3
3
2
=
=
=
-
n
m
n
m
a
a
:a
则
已知
2、
3、
9
125
1
2
_____
__________
)
5
.
0
(
)
2
(
2013
2012
=
-
-
解:∵210=a2
∴(25)2=a2
即a=25=32
又∵210=4b
∴(22)5=45=4b
即b=5
∴ab=325
2、已知a=8131,b=2741,c=961,则a、b、c的大小关系是( )
A、a>b>c B、a>c>b
C、ac>a
A
同底数幂的除法
练习十一
(1)a ÷a (2)(-a)÷(-a)
(3)(2a)÷(2a) (4) (-a)÷(-a)
(5)(p )÷p (6)a ÷(-a )
(7)m ÷m ×m (8)(a ) ÷a
练习十二
思考:1、已知210=a2=4b(其中a,b为正整数),求ab的值。
小结:
(1)掌握幂的运算的一些性质及字母的表示方法。
(2)会运用性质完成有关的计算。
(3)注意幂的四种运算的区别。
(4)体会性质的逆运用。
单击此处编辑母版标题样式
*
*
*
单击此处编辑母版副标题样式
第八章 幂的运算
复习目标
1、掌握幂的运算性质。
2、会用语言和公式表述幂的运算的性质。
3、灵活运用幂的运算性质求值。
幂的运算
同底数幂的乘法
同底数幂的除法
积的乘方
幂的乘方
同底数幂的乘法法则:
am·an=am+n
其中m,n都是正整数
语言叙述:
同底数幂相乘,底数不变,指数相加。
字母表示:
学习指导一
幂的乘方法则:
(am)n=amn
其中m,n都是正整数
语言叙述:幂的乘方,底 数不变,指数相乘。
字母表示:
学习指导二
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
(am)n=amn
am·an=am+n
练习一、计算( 口答)
1011
a10
x10
x9
(2) a7 ·a3 =
(3) x5 ·x5 =
(4) x5 ·x ·x3 =
(1) 105×106=
(1)(105)6=
(2)(a7)3 =
(3)(x5)5 =
(4)(y3)2· (y2)3=
1030
a21
x25
y12
y 6 · y 6 =
??练习二、计算( 口答)
102m+1
①10m·10m-1·100=
②3×27×9×3m=
3m+6
练习三、??计算:
③(m-n)4·(m-n) 5·(n-m)6=
④ (x-2y)4·(2y-x) 5·(x-2y)6=
(m-n)15
(2y-x)15
1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x(x5)m (D) xx5xm
c
练习四、选择
2.x14不可以写成( )
(A) x5(x3)3
(B) (-x)(-x2)(-x3)(-x8)
(C) (x7)7
(D) x3x4x5x2
c
3.计算(-32)5-(-35)2的结果是( )
(A)0 (B) -2×310
(C)2×310(D) -2×37
B
2、在xm-1·( )=x2m+1中,括号内应填写的代数式是( )
A、x2m B、x2m+1
C、x2m+2 D、xm+2
D
(1).已知:am=7,bm=4, 求(ab)2m的值。
练习五、??计算:
(2).已知:x+4y-3=0,
求2x●16y的值。
8
练习六:
1、若 am = 2,则a3m =_____.
2、若 mx = 2,my = 3 ,则
mx+y =____,m3x+2y =______.
6
72
m =m m
x
x+y
y
=6
8
动脑筋!
m =(m )? (m )?
3x+2y
x
y
=72
学习指导三
积的乘方的法则:
(ab)m =ambm
其中m是正整数
语言叙述:
积的乘方,等于把积的每一个因式分别乘方,再把所得的积相乘。
字母表示:
(1) (ab) 2 =
(2)(ab)3 =
(3)(ab)4 =
练习七、计算( 口答)
2
2
a
b
3
3
a
b
4
4
a
b
(1)(2b)3
(3)(-a)3
(4)(-3x)4
=23b3
=8b3
=22×(a3)2
=4a6
=(-1)3 ?a3
= -a3
=(-3)4 ? x4
= 81 x4
(2)(2a)3
1.判断下列计算是否正确,并说明理由:
(1)(xy3)2=xy6
(2)(-2x)3=-2x3
x?y6
-8x3
练习九
2.计算:
(1)(3a)2
(2)(-3a)3
(3)(ab2)2
(4)(-2×103)3
=(-3)3a3=-27a3
=a2(b2)2=a2b4
=(-2)3×(103)3=-8×109
=32a2=9a2
(3)-82000×(-0.125)2001
=
=
=
=
(2)(-4)2005×(0.25)2005
=
=
(1)24×44×0.1254
=
=
(2×4×0.125)4
1
(-4×0.25)2005
-1
练习十
-82000×(-0.125)2000× (-0.125)
-82000×0.1252000× (-0.125)
-(8×0.125)2000× (-0.125)
-1× (-0.125) = 0.125
逆 用 法 则 进 行 计 算
学习指导四
字母表示
语言叙述
同底数幂相除,底数不变,指数相减。
a ÷ a =a
m
n
m-n
m 、n为正整数,m>n且a≠0
8
3
10
3
6
4
3
2
5
10
3
2
8
2
3
2
3
4
1、下列算式中,
①a3·a3=2a3;②10×109=1019;③(xy2)3=xy6;④a3n÷an=a3.其中错误的是( )
A、1个 B、2个
C、3个 D、4个
D
_______
,
5
,
3
3
2
=
=
=
-
n
m
n
m
a
a
:a
则
已知
2、
3、
9
125
1
2
_____
__________
)
5
.
0
(
)
2
(
2013
2012
=
-
-
解:∵210=a2
∴(25)2=a2
即a=25=32
又∵210=4b
∴(22)5=45=4b
即b=5
∴ab=325
2、已知a=8131,b=2741,c=961,则a、b、c的大小关系是( )
A、a>b>c B、a>c>b
C、a
A
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
