苏科版 七年级下册 数学课件 9.1单项式乘单项式(共17张)
文档属性
| 名称 | 苏科版 七年级下册 数学课件 9.1单项式乘单项式(共17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 291.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 20:36:25 | ||
图片预览






文档简介
(1)系数相乘
单项式乘以单项式法则:
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
9.1 单项式乘单项式
你是如何计算(2×103)×(3×105)的?
你是如何计算3a·4a的?
(2×103)×(3×105)
乘法交换律
乘法结合律
3a·4a
乘法交换律
乘法结合律
= 2×3×103×105 -----( )
=(2×3)×(103×105)-----( )
= 6 ×108
= 3 ×4·a·a-----( )
= (3 ×4)·(a·a) -----( )
=12a2
a
b
将几台型号相同的电视机叠放在一起组成 “电视墙”,你会计算这块“电视墙”的面积吗?
口答:
(1)2x3·5x2=
(2)- 4x2y · 5xy=
(3)-2x2 ·(-3xy2)=
10x5
- 20x3y2
6x3y2
你能总结出怎样进行单项式乘以单项式吗?
(2)相同字母的幂相乘
(3)只在一个单项式中出
现的字母,则连同它的
指数一起作为积的一个
因式。
注意符号
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。
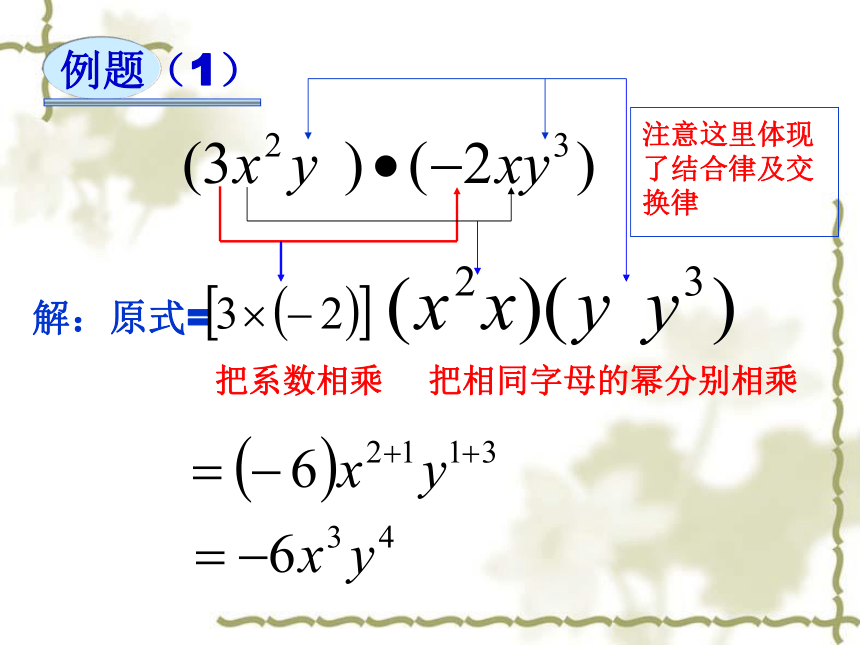
例题(1)
解:原式=
把系数相乘
把相同字母的幂分别相乘
注意这里体现了结合律及交换律
把系数相乘
解:原式=
[
]
)
3
(
)
2
(
-
-
×
例题(2)
其余字母连同它的指数不变
2
a·a
b3c.
把相同字母的幂分别相乘
z
下面的计算是否正确?如果有错误,请改正.
(1)3a3· 4a4= 7 a7 ( )
(2) -2x4·3x2= 6x6 ( )
(3) 2b3·4b3= 8b3 ( )
(4)-4x2y3·5xy2z=-20x3y5 ( )
12
×
×
×
×
-6
6
例2 计算
(-2a2)3 ·(-3a3)2
观察一下,例2比例1多了什么运算?
例1 计算
(1) 3x2y·(-2xy3)
(2) (-5a2b3)·(-4b2c)
注意:
(1)当底数不同时,先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
讨论解答:遇到积的乘方怎么办?运算时应先算什么?(同位或前后位讨论一下)
(1) 0.25a2 ·4a
a3b2·( abc)
3a2bc·( ab)
(-0.1abc)·10ab2c
(5) -8a2b·(-a3b2) · b2
计算1:
(1) a2c ·(-3ab2)
(2) (-5a2b)·(-2a)2
(3) (-a3b)3·(-ab2c3)2
(4)(- ×105)3·(9×102)2
计算2:
[3(x-y)2]·[-2(x-y)3]·[0.8(x-y)]
[-2(x-y)2]2 · (y-x)3
根据图中所示条件,求阴影部分的面积
x
4x
6x
3x
1.这节课你有什么样的收获?
2.还有哪些疑问?
(1)单项式乘以单项式的法则
(2)单项式乘以单项式
转化
运用乘法的交换律、结合律
有理数的乘法
幂的乘法运算
小结
(3)可以用单项式乘以单项式来解决现实生活中的问题
知识延伸
1.已知3xn-3y5-n与-8x3my2n的积
是2x4y9的同类项,求m、n的值.
2.若(2anb· abm)3=8a9b15
求m+n的值
① (a2)2(—2ab);
② 5m· ( abm) · (—am);
③ 0.5an—1bm—2c · (— 0.2a2b3);
(m,n是整数)
④ —10×(0.3×102)(0.4×105);
⑤ X3y2 · (— 2xy2)+
(— 2x2y) · ( xy) · 3xyz;
单项式乘以单项式法则:
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
9.1 单项式乘单项式
你是如何计算(2×103)×(3×105)的?
你是如何计算3a·4a的?
(2×103)×(3×105)
乘法交换律
乘法结合律
3a·4a
乘法交换律
乘法结合律
= 2×3×103×105 -----( )
=(2×3)×(103×105)-----( )
= 6 ×108
= 3 ×4·a·a-----( )
= (3 ×4)·(a·a) -----( )
=12a2
a
b
将几台型号相同的电视机叠放在一起组成 “电视墙”,你会计算这块“电视墙”的面积吗?
口答:
(1)2x3·5x2=
(2)- 4x2y · 5xy=
(3)-2x2 ·(-3xy2)=
10x5
- 20x3y2
6x3y2
你能总结出怎样进行单项式乘以单项式吗?
(2)相同字母的幂相乘
(3)只在一个单项式中出
现的字母,则连同它的
指数一起作为积的一个
因式。
注意符号
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。
例题(1)
解:原式=
把系数相乘
把相同字母的幂分别相乘
注意这里体现了结合律及交换律
把系数相乘
解:原式=
[
]
)
3
(
)
2
(
-
-
×
例题(2)
其余字母连同它的指数不变
2
a·a
b3c.
把相同字母的幂分别相乘
z
下面的计算是否正确?如果有错误,请改正.
(1)3a3· 4a4= 7 a7 ( )
(2) -2x4·3x2= 6x6 ( )
(3) 2b3·4b3= 8b3 ( )
(4)-4x2y3·5xy2z=-20x3y5 ( )
12
×
×
×
×
-6
6
例2 计算
(-2a2)3 ·(-3a3)2
观察一下,例2比例1多了什么运算?
例1 计算
(1) 3x2y·(-2xy3)
(2) (-5a2b3)·(-4b2c)
注意:
(1)当底数不同时,先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
讨论解答:遇到积的乘方怎么办?运算时应先算什么?(同位或前后位讨论一下)
(1) 0.25a2 ·4a
a3b2·( abc)
3a2bc·( ab)
(-0.1abc)·10ab2c
(5) -8a2b·(-a3b2) · b2
计算1:
(1) a2c ·(-3ab2)
(2) (-5a2b)·(-2a)2
(3) (-a3b)3·(-ab2c3)2
(4)(- ×105)3·(9×102)2
计算2:
[3(x-y)2]·[-2(x-y)3]·[0.8(x-y)]
[-2(x-y)2]2 · (y-x)3
根据图中所示条件,求阴影部分的面积
x
4x
6x
3x
1.这节课你有什么样的收获?
2.还有哪些疑问?
(1)单项式乘以单项式的法则
(2)单项式乘以单项式
转化
运用乘法的交换律、结合律
有理数的乘法
幂的乘法运算
小结
(3)可以用单项式乘以单项式来解决现实生活中的问题
知识延伸
1.已知3xn-3y5-n与-8x3my2n的积
是2x4y9的同类项,求m、n的值.
2.若(2anb· abm)3=8a9b15
求m+n的值
① (a2)2(—2ab);
② 5m· ( abm) · (—am);
③ 0.5an—1bm—2c · (— 0.2a2b3);
(m,n是整数)
④ —10×(0.3×102)(0.4×105);
⑤ X3y2 · (— 2xy2)+
(— 2x2y) · ( xy) · 3xyz;
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
