人教高中数学必修二1.1.1柱、锥、台、球的结构特征 课件(34张ppt)
文档属性
| 名称 | 人教高中数学必修二1.1.1柱、锥、台、球的结构特征 课件(34张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 23:17:44 | ||
图片预览








文档简介
(共34张PPT)
我要问
这些图片中的物体具有什么样的几何
结构特征?你能对它们进行分类吗?
我来答
上图中的物体大体可分为两大类.
其中(2),(5),(7),(9),(13),(14),(15),(16)
具有相同的特点:组成几何体的每个面都是平面图形,并且都是平面多边形;
(1),(3),(4),(6),(8),(10),(11),(12)
具有相同的特点:组成它们的面不全是平面图形.
想一想?
我们应该给上述两大类几何
体取个什么名字才好呢?
空间几何体:
对于空间的物体,如果只考虑它的的形状、大小和位置,而不考虑物体的其他性质,从中抽象出来的空间图形叫做空间几何体
1.1
柱、锥、台、球的结构特征
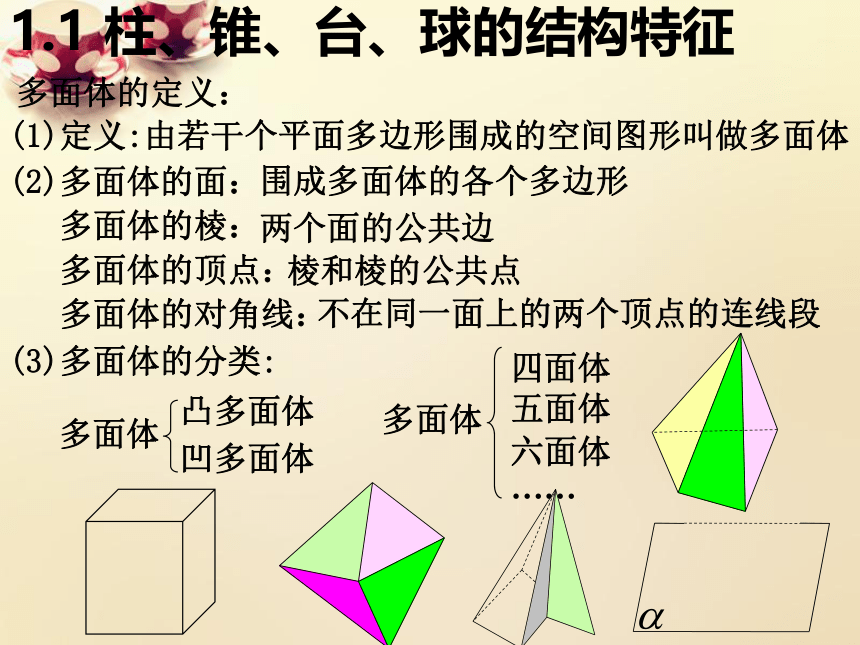
多面体的定义:
(1)定义:由若干个平面多边形围成的空间图形叫做多面体
(2)多面体的面:
多面体的棱:
多面体的顶点:
多面体的对角线:
围成多面体的各个多边形
两个面的公共边
棱和棱的公共点
不在同一面上的两个顶点的连线段
(3)多面体的分类:
凸多面体
凹多面体
多面体
四面体
多面体
五面体
六面体
……
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
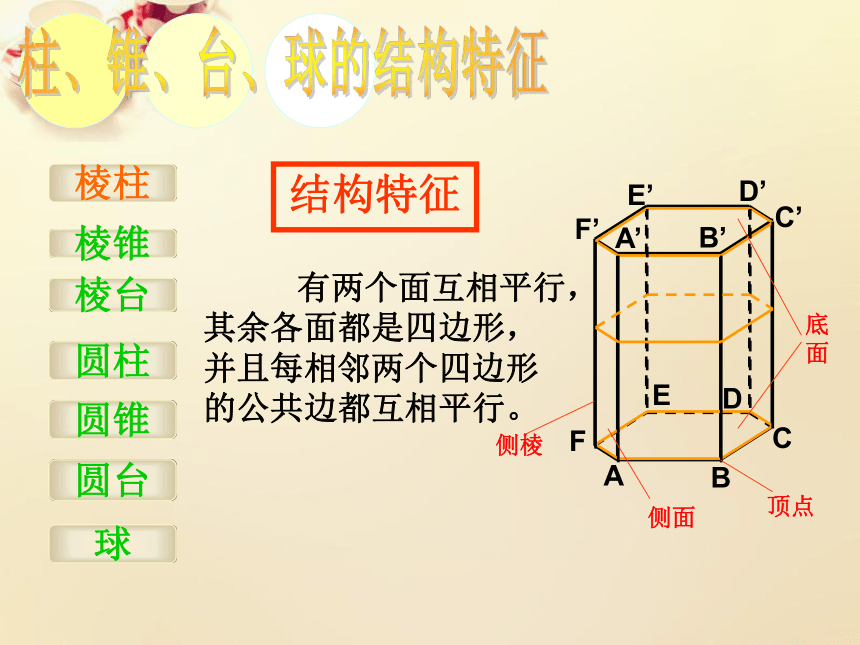
结构特征
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行。
侧棱
侧面
底面
顶点
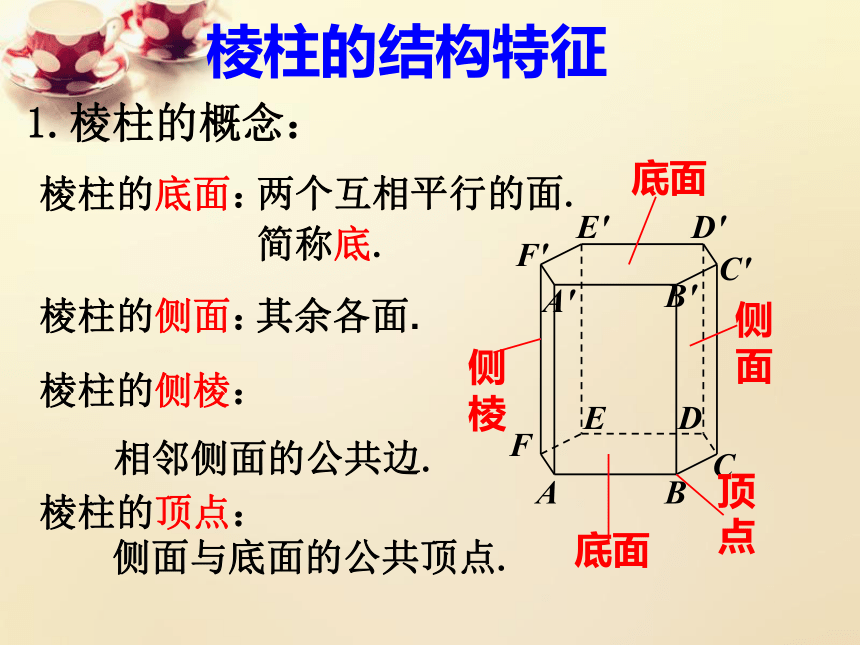
棱柱的结构特征
1.棱柱的概念:
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
棱柱的底面:
两个互相平行的面.
简称底.
底面
底面
棱柱的侧面:
其余各面.
棱柱的侧棱:
相邻侧面的公共边.
棱柱的顶点:
侧面与底面的公共顶点.
侧
面
侧
棱
顶
点
棱柱的结构特征
2.棱柱的分类:
按底面多边形的边数来分
三棱柱
四棱柱
五棱柱
3.棱柱的表示:
棱柱ABC-
A'B'C'
用表示底面各顶点的字母表示
D'
A
B
C
D
E
A'
B'
C'
E'
A
B
C
D
A'
B'
C'
D'
A
B
C
A'
B'
C'
棱柱的结构特征
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
思考:对于棱柱,
1.侧棱长相等吗?
侧面是什么四边形?
平行四边形
相等
2.两个底面多边形是什么关系?
与平行于底面的截面呢?
全等
3.过不相邻的两条侧棱的截面是什么四边形?
平行四边形
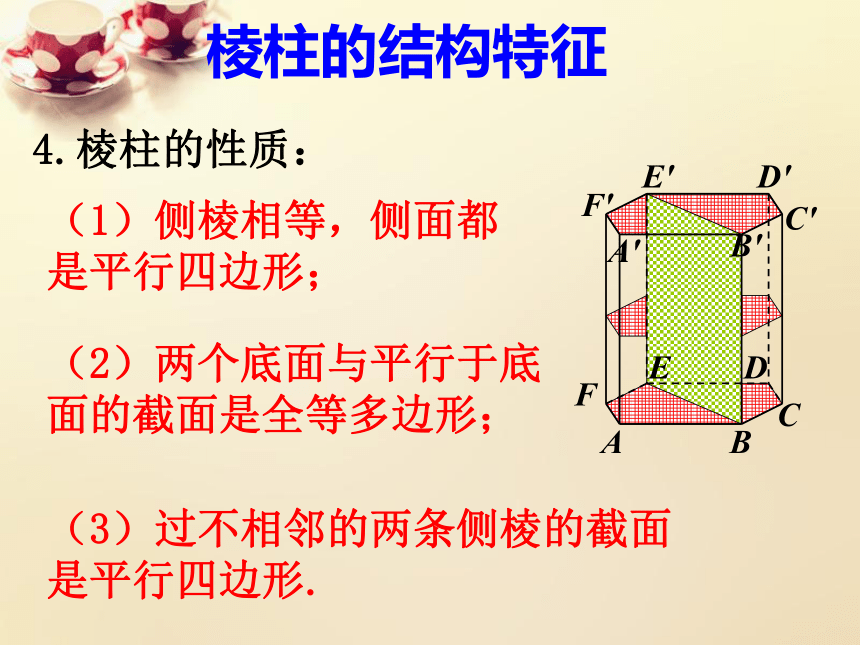
棱柱的结构特征
4.棱柱的性质:
(1)侧棱相等,侧面都是平行四边形;
(2)两个底面与平行于底面的截面是全等多边形;
(3)过不相邻的两条侧棱的截面是平行四边形.
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
例2.有两个面互相平行,其余各面都是
平行四边形的几何体是不是棱柱?
长方体:
侧面和底面都是矩形的棱柱.
正方体:
侧面和底面都是正方形的棱柱.
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
A
B
C
D
顶点
侧面
侧棱
底面
结构特征
有一个面是多边形,其余各面都是有一个公共顶点的三角形。
棱锥的结构特征
1.棱锥的概念:
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥.
棱锥的结构特征
1.棱锥的概念:
棱锥的底面:
多边形面.
简称底.
底面
顶点
棱锥的侧面:
有公共顶点的
各个三角形面.
棱锥的侧棱:
相邻侧面的公共边.
棱锥的顶点:
各侧面的公共顶点.
侧
棱
侧
面
棱锥的结构特征
2.棱锥的分类:
按底面多边形的边数来分
三棱锥
四棱锥
五棱锥
3.棱锥的表示:
棱锥S-ABC
用顶点各底面各顶点的字母表示
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
A
B
C
D
A’
B’
C’
D’
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.
棱台的结构特征
1.棱台的概念:
棱台的底面:
原棱锥的底面和截面分别叫做棱台的下底面和上底面。
下底面
侧
棱
顶
点
侧
面
上底面
棱台的结构特征
1.棱台的概念:
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
2.棱台的分类:
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
三棱台
四棱台
五棱台
3.棱台的表示:
棱台ABCD-A‘B’C‘D’
用顶点各底面各顶点的字母表示
B’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
A
A’
O
B
O’
轴
底面
侧面
母线
结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
顶点
A
B
O
底面
轴
侧面
母线
结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
O’
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
半径
球心
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体.
球的结构特征
球:以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的几何体叫做球体。
直径
O
A
B
C
球心
大圆
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
(1)棱柱与圆柱统称为柱体。
(2)棱锥与圆锥统称为锥体。
旋转体
(2)棱台与圆台统称为台体。
多面体
几何体的分类
前面提到的四种几何体:棱柱、棱锥、圆柱、圆锥,可以怎样分类?
柱体
锥体
锥
体
柱
体
台
体
柱、锥、台体的关系
棱柱、棱锥、棱台之间有什么关系?圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什么关系?
上底扩大
上底缩小
上底缩小
上底扩大
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
练习:
1、下列命题是真命题的是(
)
A
以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B
以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C
圆柱、圆锥、棱锥的底面都是圆;
D
有一个面为多边形,其他各面都是三角形的几何体是棱锥。
A
2、过球面上的两点作球的大圆,可以作(
)个。
1或无数多
3.下图中不可能围成正方体的是(
)
A
D
C
B
B
4.在棱柱中………………..(
)
A
.
只有两个面平行
B
.
所有的棱都相等
C
.
所有的面都是平行四边形
D
.
两底面平行,并且各侧棱也平行
D
知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
我要问
这些图片中的物体具有什么样的几何
结构特征?你能对它们进行分类吗?
我来答
上图中的物体大体可分为两大类.
其中(2),(5),(7),(9),(13),(14),(15),(16)
具有相同的特点:组成几何体的每个面都是平面图形,并且都是平面多边形;
(1),(3),(4),(6),(8),(10),(11),(12)
具有相同的特点:组成它们的面不全是平面图形.
想一想?
我们应该给上述两大类几何
体取个什么名字才好呢?
空间几何体:
对于空间的物体,如果只考虑它的的形状、大小和位置,而不考虑物体的其他性质,从中抽象出来的空间图形叫做空间几何体
1.1
柱、锥、台、球的结构特征
多面体的定义:
(1)定义:由若干个平面多边形围成的空间图形叫做多面体
(2)多面体的面:
多面体的棱:
多面体的顶点:
多面体的对角线:
围成多面体的各个多边形
两个面的公共边
棱和棱的公共点
不在同一面上的两个顶点的连线段
(3)多面体的分类:
凸多面体
凹多面体
多面体
四面体
多面体
五面体
六面体
……
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行。
侧棱
侧面
底面
顶点
棱柱的结构特征
1.棱柱的概念:
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
棱柱的底面:
两个互相平行的面.
简称底.
底面
底面
棱柱的侧面:
其余各面.
棱柱的侧棱:
相邻侧面的公共边.
棱柱的顶点:
侧面与底面的公共顶点.
侧
面
侧
棱
顶
点
棱柱的结构特征
2.棱柱的分类:
按底面多边形的边数来分
三棱柱
四棱柱
五棱柱
3.棱柱的表示:
棱柱ABC-
A'B'C'
用表示底面各顶点的字母表示
D'
A
B
C
D
E
A'
B'
C'
E'
A
B
C
D
A'
B'
C'
D'
A
B
C
A'
B'
C'
棱柱的结构特征
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
思考:对于棱柱,
1.侧棱长相等吗?
侧面是什么四边形?
平行四边形
相等
2.两个底面多边形是什么关系?
与平行于底面的截面呢?
全等
3.过不相邻的两条侧棱的截面是什么四边形?
平行四边形
棱柱的结构特征
4.棱柱的性质:
(1)侧棱相等,侧面都是平行四边形;
(2)两个底面与平行于底面的截面是全等多边形;
(3)过不相邻的两条侧棱的截面是平行四边形.
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
例2.有两个面互相平行,其余各面都是
平行四边形的几何体是不是棱柱?
长方体:
侧面和底面都是矩形的棱柱.
正方体:
侧面和底面都是正方形的棱柱.
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
A
B
C
D
顶点
侧面
侧棱
底面
结构特征
有一个面是多边形,其余各面都是有一个公共顶点的三角形。
棱锥的结构特征
1.棱锥的概念:
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥.
棱锥的结构特征
1.棱锥的概念:
棱锥的底面:
多边形面.
简称底.
底面
顶点
棱锥的侧面:
有公共顶点的
各个三角形面.
棱锥的侧棱:
相邻侧面的公共边.
棱锥的顶点:
各侧面的公共顶点.
侧
棱
侧
面
棱锥的结构特征
2.棱锥的分类:
按底面多边形的边数来分
三棱锥
四棱锥
五棱锥
3.棱锥的表示:
棱锥S-ABC
用顶点各底面各顶点的字母表示
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
A
B
C
D
A’
B’
C’
D’
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.
棱台的结构特征
1.棱台的概念:
棱台的底面:
原棱锥的底面和截面分别叫做棱台的下底面和上底面。
下底面
侧
棱
顶
点
侧
面
上底面
棱台的结构特征
1.棱台的概念:
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
2.棱台的分类:
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
三棱台
四棱台
五棱台
3.棱台的表示:
棱台ABCD-A‘B’C‘D’
用顶点各底面各顶点的字母表示
B’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
A
A’
O
B
O’
轴
底面
侧面
母线
结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
顶点
A
B
O
底面
轴
侧面
母线
结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
O’
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
半径
球心
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体.
球的结构特征
球:以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的几何体叫做球体。
直径
O
A
B
C
球心
大圆
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
(1)棱柱与圆柱统称为柱体。
(2)棱锥与圆锥统称为锥体。
旋转体
(2)棱台与圆台统称为台体。
多面体
几何体的分类
前面提到的四种几何体:棱柱、棱锥、圆柱、圆锥,可以怎样分类?
柱体
锥体
锥
体
柱
体
台
体
柱、锥、台体的关系
棱柱、棱锥、棱台之间有什么关系?圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什么关系?
上底扩大
上底缩小
上底缩小
上底扩大
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
练习:
1、下列命题是真命题的是(
)
A
以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B
以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C
圆柱、圆锥、棱锥的底面都是圆;
D
有一个面为多边形,其他各面都是三角形的几何体是棱锥。
A
2、过球面上的两点作球的大圆,可以作(
)个。
1或无数多
3.下图中不可能围成正方体的是(
)
A
D
C
B
B
4.在棱柱中………………..(
)
A
.
只有两个面平行
B
.
所有的棱都相等
C
.
所有的面都是平行四边形
D
.
两底面平行,并且各侧棱也平行
D
知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
