六年级数学下册试题 一课一练《图形与几何--立体图形的认识与测量(二)》-人教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《图形与几何--立体图形的认识与测量(二)》-人教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 732.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 14:08:23 | ||
图片预览


文档简介
《图形与几何--立体图形的认识与测量(二)》
一、计算题
1.求如图图形的表面积.(单位:厘米)
2.有一个半圆柱如图,已知它的底面直径是20厘米,高是8厘米,求它的表面积.
3.仔细观察下面图形的特点,然后用较简便的方法求出这个图形的体积:(单位:厘米)
4.图形计算
求立体图形的体积。单位(分米)
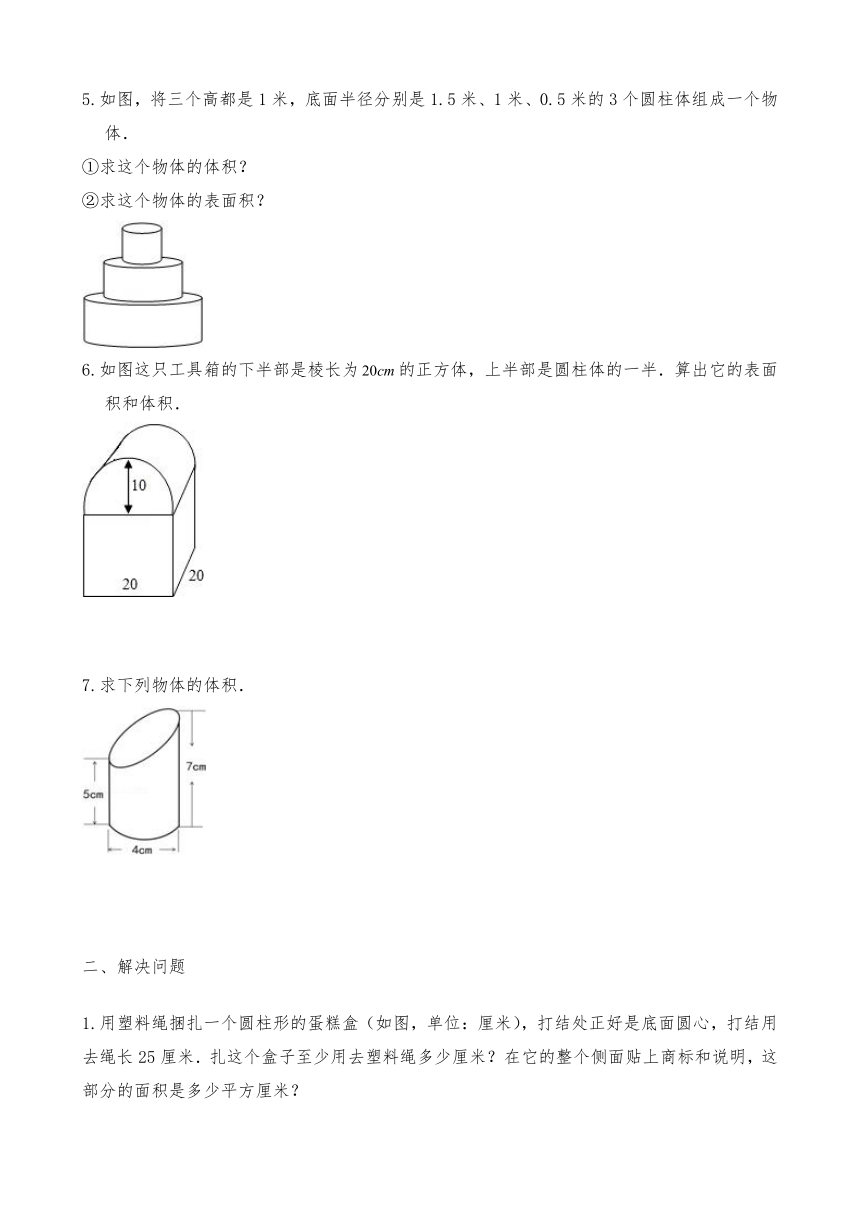
5.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体.
①求这个物体的体积?
②求这个物体的表面积?
6.如图这只工具箱的下半部是棱长为的正方体,上半部是圆柱体的一半.算出它的表面积和体积.
7.求下列物体的体积.
二、解决问题
1.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
2.砌一个圆柱形的水池,底面直径6米,深3米.在池的周围和底面抹上水泥,每平方米用水泥5千克,大约要用水泥多少千克?(得数保留整千克数)
3.一根圆柱形水管,横截面的半径是5厘米,长是1.2米,做100节这样的水管要铁皮多少平米?
4.把一个长12厘米,宽6厘米的长方形纸板沿长旋转一周,得到一个圆柱体,这个圆柱体的侧面积是多少?
5.如图,是用塑料薄膜覆盖的蔬菜大棚,长16米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
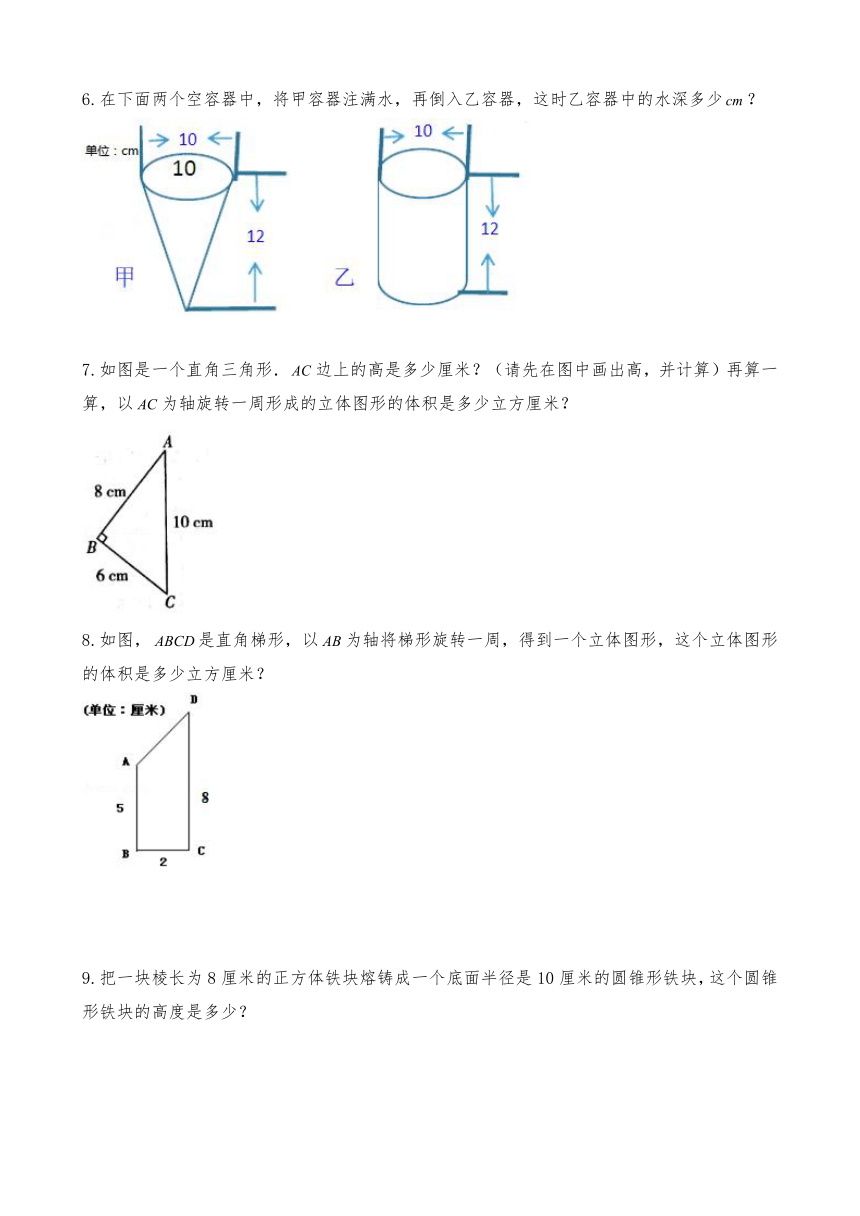
6.在下面两个空容器中,将甲容器注满水,再倒入乙容器,这时乙容器中的水深多少?
7.如图是一个直角三角形.边上的高是多少厘米?(请先在图中画出高,并计算)再算一算,以为轴旋转一周形成的立体图形的体积是多少立方厘米?
8.如图,是直角梯形,以为轴将梯形旋转一周,得到一个立体图形,这个立体图形的体积是多少立方厘米?
9.把一块棱长为8厘米的正方体铁块熔铸成一个底面半径是10厘米的圆锥形铁块,这个圆锥形铁块的高度是多少?
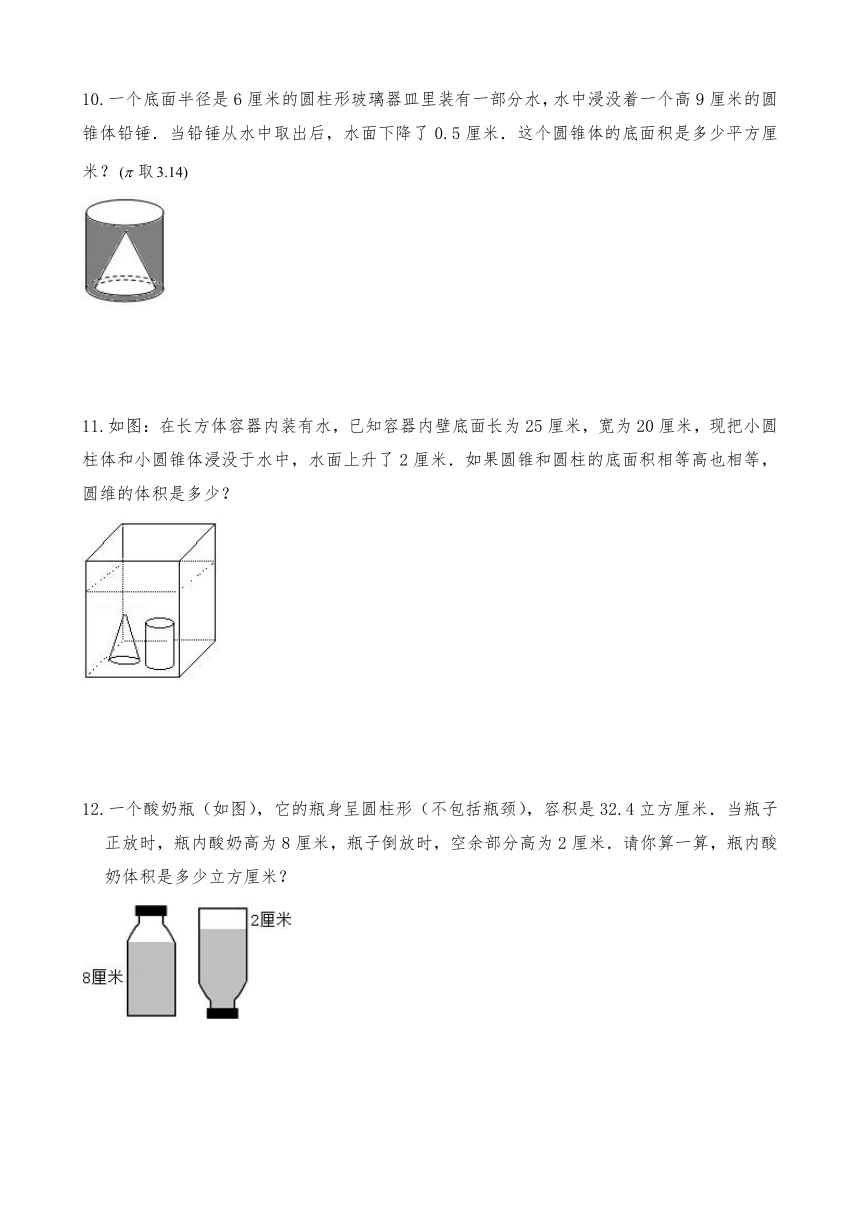
10.一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤.当铅锤从水中取出后,水面下降了0.5厘米.这个圆锥体的底面积是多少平方厘米?取
11.如图:在长方体容器内装有水,已知容器内壁底面长为25厘米,宽为20厘米,现把小圆柱体和小圆锥体浸没于水中,水面上升了2厘米.如果圆锥和圆柱的底面积相等高也相等,圆维的体积是多少?
12.一个酸奶瓶(如图),它的瓶身呈圆柱形(不包括瓶颈),容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
13.有甲、乙两只圆柱形玻璃杯,其内直径依次是18厘米、12厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?
14.有一个高8厘米,容量为50毫升的圆形容器,里面装满了水,现把长16厘米的圆柱垂直放入,使的底和的底面接触,这时一部分水从容器中溢出,当把从拿走后,中的水的高度只有6厘米,求圆柱体的体积是多少?
15.有一种容器,瓶颈以下部分呈圆柱形,内有水.现在容器中装有一些水,正放时水的高度为,倒放时空余部分的高度为.问:容器的容积是多少毫升?
16.在底面长60厘米、宽40厘米的长方形鱼缸中竖直放入一个圆柱体氧气泵,有在水面上,其余被水浸没.此时水位比放入前上升了2厘米,氧气泵的体积是多少立方厘米?
17.如图所示,某机器零件中间是一个棱长为2厘米的正方体,两边各是圆柱体的一半,求这个零件的表面积和体积.
18.小明把一块橡皮泥揉成圆柱形,切成三块(如图),表面积增加了50.24平方厘米,切成四块(如图),表面积增加了96平方厘米,这块橡皮泥的体积是多少立方厘米?
19.将一个圆锥从顶点沿底面直径切开,其表面积比原来增加了60平方厘米,如果圆锥的高是6厘米,则圆锥的体积是多少立方厘米?
20.把3个长6厘米,底面积相等的圆柱体拼成一个大圆柱,表面积减少了18.84立方厘米,拼成的大圆柱的体积是多少立方厘米?
21.一个底面周长是43.96厘米,高为8厘米的圆柱,沿着高切成两个同样大小的半圆柱体,表面积增加了多少?
22.把一个圆柱按如图1沿直径方向切成两个半圆柱,表面积增加,按图2方式切成两个圆柱,表面积就会增加,求这个圆柱的体积.
23.如图所示,把底面周长18.84厘米,高10厘米的圆柱切成若干等分,拼成一个近似的长方体.这个长方体的底面积、表面积和体积各是多少?
24.一段体积是52.8立方分米的圆柱木料,切削成一个最大的圆锥体,削去部分的体积是多少立方分米?
25.一个正方体木块棱长为,把它切削成一个最大的圆锥体.求这个圆锥体与原来正方体的体积比是多少?
26.一个底面直径是4厘米的圆锥如图,从顶点沿着高将它切成两半后,表面积增加了24平方分米.这个圆锥的体积是多少平方厘米?
27.把一个棱长为的正方体铁块放入一个圆柱形容器内,完全浸没后水面上升了,如果把一个圆锥形铅块放入圆柱容器中,完全浸没后水面上升了,求这个圆锥形铅块的体积.
28.有甲乙两只圆柱形水桶,甲水桶的底面半径是.乙水桶的底面半径是.甲水桶里没有水,乙水桶里有水且高度是,现把乙水桶里的水倒一部分给甲水桶,使两只水桶里的水的高度一样.求这时甲水桶里有水多少立方厘米?
29.一个圆柱形水桶里放入一段半径5厘米的圆钢,把它全部放入水中,桶里的水面上升了9厘米,如果把水中的圆钢提起,使它露出水面8厘米,那么桶里的水面就下降4厘米,求圆钢的体积.取
30.一个圆柱形水桶,底面半径为,里面盛有深的水,现将一个底面周长为的圆锥形铁块完全浸没在水中,水面上升了.圆锥形铁块的高度是多少?取
31.圆柱的底面半径和高都是2厘米,把它浸入一个均匀水槽内的水中,量得水位上升了1厘米.再把一个底面直径为6厘米的圆锥浸入水中,水位又上升了4.5厘米.求圆锥的高.
32.在一个底面积为34平方厘米的圆柱形容器中,放入等底等高的一根圆柱形物体和一个圆锥形物体,水面上升10厘米,圆柱有露出水面,圆锥完全浸没,圆锥的体积是多少立方厘米?
33.一个圆柱形木块按图甲中的方式切成形状、大小相同的四块,表面积增加了;按图乙中的方式切成形状、大小相同的三块,表面积增加了.若把它削成一个最大的圆锥,体积减小多少立方厘米?
34.如图,在密封的容器中装有一些水,水面距底部的高度是.如果将这个容器倒过来,你能求出这时水面距底部的高度是多少厘米吗?
答案
一、计算题
1.解:
(平方厘米)
答:这个图形的表面积是2041平方厘米.
2.解:
(平方厘米)
答:它的表面积是725.2平方厘米.
3.解:,
,
,
(立方厘米);
答:这个图形的体积是150.72平方厘米.
4.解:
(立方分米),
答:这个立体图形的体积是3532.5立方分米.
5.解:(1),
,
,
(立方米),
答:这个物体的体积是10.99立方米.
(2)大圆柱的表面积:,
,
(平方米),
中圆柱侧面积:(平方米),
小圆柱侧面积:(平方米),
这个物体的表面积:(平方米);
答:这个物体的表面积是32.97平方米.
6.解:表面积:
,
,
,
(平方厘米);
体积:
,
,
,
(立方厘米);
答:它的表面积是2942平方厘米,体积是11140立方厘米.
7.解:
(立方厘米),
答:图中物体的体积是75.36立方厘米.
二、解决问题
1.解:(1),
,
(厘米),
面积:,
,
(平方厘米);
答:扎这个盒子至少用去塑料绳545厘米,在它的整个侧面贴上商标和说明,这部分的面积是2355平方厘米.
2.解:需要抹水泥的面积是:
,
,
,
(平方米),
(千克),
答:大约要用水泥424千克.
3.解:5厘米米,
(平方米);
答:做100节这样的水管至少需要37.68平方米的铁皮.
4.解:,
,
,
(平方厘米),
答:这个圆柱体的侧面积是452.16平方厘米.
5.解:(1)(平方米)
答:这个大棚的种植面积是32平方米.
(2)
(平方米)
答:覆盖在这个大棚上的塑料薄膜约有53.38平方米.
6.解:(厘米)
答:乙容器中的水深4厘米.
7.解:边上的高:
如图:
(厘米)
(立方厘米)
答:以为轴旋转一周形成的立体图形的体积是241.152立方厘米.
8.解:如下图:
(立方厘米),
答:这个立体图形的体积是87.92立方厘米.
9.解:(立方厘米)
(厘米)
答:这个圆锥形铁块的高大约是4.89厘米.
10.解:容器水下降的体积:
(立方厘米);
圆锥的底面积:
(平方厘米);
答:这个圆锥体的底面积是18.84平方厘米.
11.解:圆锥和圆柱的体积和:
(立方厘米);
(立方厘米),
答:圆锥体的体积是250立方厘米.
12.解:(厘米),
(立方厘米),
答:瓶内酸奶体积是25.92立方厘米.
13.解:
(厘米)
答:这时乙杯中的水位上升了4.5厘米.
14.解:圆形容器的底面积:
(平方厘米);
溢出水的体积,即放入容器的圆柱的体积:
,
,
(毫升);
圆柱体的体积是:
,
,
(立方厘米);
答:圆柱体的体积是25立方厘米.
15.解:根据题意画示意图如下:
解:
毫升
答:容器的容积是多少毫升660毫升.
16.解:
(立方厘米)
答:氧气泵的体积是5760立方厘米.
17.解:
(平方厘米);
(立方厘米);
答:这个零件的表面积是28.56平方厘米,体积是14.28立方厘米.
18.解:根据题意得
所以半径是2厘米.
(厘米)
(立方厘米)
答:这块橡皮泥的体积是75.36立方厘米.
19.解:圆锥的底面直径:
(厘米);
圆锥的体积:
(立方厘米),
答:这个圆锥的体积是157立方厘米.
20.解:,
,
(立方厘米),
答:拼成的大圆柱的体积是84.78立方厘米.
21.解:底面直径:(厘米),
(平方厘米),
答:表面积增加了224平方厘米.
22.解:圆柱的底面积:(平方厘米),
底面半径的平方:,
因为2的平方是4,所以圆柱的底面半径是2厘米,
圆柱的高:(厘米),
体积:,
,
(立方厘米),
答:这个圆柱的体积是62.8立方厘米.
23.解:底面半径是:(厘米)
底面积是:(平方厘米)
表面积是:
(平方厘米)
体积是:
(立方厘米)
答:这个长方体的底面积是28.26平方厘米,表面积是304.92平方厘米,体积是282.6立方厘米.
24.解:(立方分米)
答:削去部分的体积是35.2立方分米.
25.解:
.
答:这个圆锥体与原来正方体的体积比是.
26.解:24平方分米平方厘米
(厘米)
(立方厘米)
答:这个圆锥的体积是2512立方厘米.
27.解:
(立方分米)
答:这个圆锥形铅块的体积是81立方分米.
28.
(立方厘米);
答:这时甲水桶里有水1808.64立方厘米.
29.解:设圆钢的高为厘米,
圆钢体积
水桶底面积
因为下降的水的体积水面上圆钢的体积
,
,
,
,
,
圆钢体积(立方厘米).
答:这段圆钢的体积是1413立方厘米.
30.解:设圆锥形铁块的高是厘米
,
,
;
答:圆锥形铁块的高是60厘米.
31.解:
(平方厘米)
(厘米)
答:圆锥的高是12厘米.
32.解:放入等底等高的一根圆柱形钢材和一个圆锥以后,水面上升10厘米,
增加体积:(立方厘米),
由圆柱体和圆锥体体积公式知:等低等高的圆柱体积是圆锥体积的3倍,
设圆锥体体积为,则圆柱体体积为,
,
,
;
答:圆锥的体积是100立方厘米.
33.解:(平方厘米)
设圆柱底面半径为厘米
因为
所以
(厘米)
(立方厘米)
答:体积减小50.24立方厘米.
34.解:高6厘米的圆锥容器中水倒入等底的圆柱容器中高是(厘米)
(厘米),
答:如果将这个容器倒过来,这时水面距底部的高度是6厘米.
一、计算题
1.求如图图形的表面积.(单位:厘米)
2.有一个半圆柱如图,已知它的底面直径是20厘米,高是8厘米,求它的表面积.
3.仔细观察下面图形的特点,然后用较简便的方法求出这个图形的体积:(单位:厘米)
4.图形计算
求立体图形的体积。单位(分米)
5.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体.
①求这个物体的体积?
②求这个物体的表面积?
6.如图这只工具箱的下半部是棱长为的正方体,上半部是圆柱体的一半.算出它的表面积和体积.
7.求下列物体的体积.
二、解决问题
1.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
2.砌一个圆柱形的水池,底面直径6米,深3米.在池的周围和底面抹上水泥,每平方米用水泥5千克,大约要用水泥多少千克?(得数保留整千克数)
3.一根圆柱形水管,横截面的半径是5厘米,长是1.2米,做100节这样的水管要铁皮多少平米?
4.把一个长12厘米,宽6厘米的长方形纸板沿长旋转一周,得到一个圆柱体,这个圆柱体的侧面积是多少?
5.如图,是用塑料薄膜覆盖的蔬菜大棚,长16米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
6.在下面两个空容器中,将甲容器注满水,再倒入乙容器,这时乙容器中的水深多少?
7.如图是一个直角三角形.边上的高是多少厘米?(请先在图中画出高,并计算)再算一算,以为轴旋转一周形成的立体图形的体积是多少立方厘米?
8.如图,是直角梯形,以为轴将梯形旋转一周,得到一个立体图形,这个立体图形的体积是多少立方厘米?
9.把一块棱长为8厘米的正方体铁块熔铸成一个底面半径是10厘米的圆锥形铁块,这个圆锥形铁块的高度是多少?
10.一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤.当铅锤从水中取出后,水面下降了0.5厘米.这个圆锥体的底面积是多少平方厘米?取
11.如图:在长方体容器内装有水,已知容器内壁底面长为25厘米,宽为20厘米,现把小圆柱体和小圆锥体浸没于水中,水面上升了2厘米.如果圆锥和圆柱的底面积相等高也相等,圆维的体积是多少?
12.一个酸奶瓶(如图),它的瓶身呈圆柱形(不包括瓶颈),容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
13.有甲、乙两只圆柱形玻璃杯,其内直径依次是18厘米、12厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?
14.有一个高8厘米,容量为50毫升的圆形容器,里面装满了水,现把长16厘米的圆柱垂直放入,使的底和的底面接触,这时一部分水从容器中溢出,当把从拿走后,中的水的高度只有6厘米,求圆柱体的体积是多少?
15.有一种容器,瓶颈以下部分呈圆柱形,内有水.现在容器中装有一些水,正放时水的高度为,倒放时空余部分的高度为.问:容器的容积是多少毫升?
16.在底面长60厘米、宽40厘米的长方形鱼缸中竖直放入一个圆柱体氧气泵,有在水面上,其余被水浸没.此时水位比放入前上升了2厘米,氧气泵的体积是多少立方厘米?
17.如图所示,某机器零件中间是一个棱长为2厘米的正方体,两边各是圆柱体的一半,求这个零件的表面积和体积.
18.小明把一块橡皮泥揉成圆柱形,切成三块(如图),表面积增加了50.24平方厘米,切成四块(如图),表面积增加了96平方厘米,这块橡皮泥的体积是多少立方厘米?
19.将一个圆锥从顶点沿底面直径切开,其表面积比原来增加了60平方厘米,如果圆锥的高是6厘米,则圆锥的体积是多少立方厘米?
20.把3个长6厘米,底面积相等的圆柱体拼成一个大圆柱,表面积减少了18.84立方厘米,拼成的大圆柱的体积是多少立方厘米?
21.一个底面周长是43.96厘米,高为8厘米的圆柱,沿着高切成两个同样大小的半圆柱体,表面积增加了多少?
22.把一个圆柱按如图1沿直径方向切成两个半圆柱,表面积增加,按图2方式切成两个圆柱,表面积就会增加,求这个圆柱的体积.
23.如图所示,把底面周长18.84厘米,高10厘米的圆柱切成若干等分,拼成一个近似的长方体.这个长方体的底面积、表面积和体积各是多少?
24.一段体积是52.8立方分米的圆柱木料,切削成一个最大的圆锥体,削去部分的体积是多少立方分米?
25.一个正方体木块棱长为,把它切削成一个最大的圆锥体.求这个圆锥体与原来正方体的体积比是多少?
26.一个底面直径是4厘米的圆锥如图,从顶点沿着高将它切成两半后,表面积增加了24平方分米.这个圆锥的体积是多少平方厘米?
27.把一个棱长为的正方体铁块放入一个圆柱形容器内,完全浸没后水面上升了,如果把一个圆锥形铅块放入圆柱容器中,完全浸没后水面上升了,求这个圆锥形铅块的体积.
28.有甲乙两只圆柱形水桶,甲水桶的底面半径是.乙水桶的底面半径是.甲水桶里没有水,乙水桶里有水且高度是,现把乙水桶里的水倒一部分给甲水桶,使两只水桶里的水的高度一样.求这时甲水桶里有水多少立方厘米?
29.一个圆柱形水桶里放入一段半径5厘米的圆钢,把它全部放入水中,桶里的水面上升了9厘米,如果把水中的圆钢提起,使它露出水面8厘米,那么桶里的水面就下降4厘米,求圆钢的体积.取
30.一个圆柱形水桶,底面半径为,里面盛有深的水,现将一个底面周长为的圆锥形铁块完全浸没在水中,水面上升了.圆锥形铁块的高度是多少?取
31.圆柱的底面半径和高都是2厘米,把它浸入一个均匀水槽内的水中,量得水位上升了1厘米.再把一个底面直径为6厘米的圆锥浸入水中,水位又上升了4.5厘米.求圆锥的高.
32.在一个底面积为34平方厘米的圆柱形容器中,放入等底等高的一根圆柱形物体和一个圆锥形物体,水面上升10厘米,圆柱有露出水面,圆锥完全浸没,圆锥的体积是多少立方厘米?
33.一个圆柱形木块按图甲中的方式切成形状、大小相同的四块,表面积增加了;按图乙中的方式切成形状、大小相同的三块,表面积增加了.若把它削成一个最大的圆锥,体积减小多少立方厘米?
34.如图,在密封的容器中装有一些水,水面距底部的高度是.如果将这个容器倒过来,你能求出这时水面距底部的高度是多少厘米吗?
答案
一、计算题
1.解:
(平方厘米)
答:这个图形的表面积是2041平方厘米.
2.解:
(平方厘米)
答:它的表面积是725.2平方厘米.
3.解:,
,
,
(立方厘米);
答:这个图形的体积是150.72平方厘米.
4.解:
(立方分米),
答:这个立体图形的体积是3532.5立方分米.
5.解:(1),
,
,
(立方米),
答:这个物体的体积是10.99立方米.
(2)大圆柱的表面积:,
,
(平方米),
中圆柱侧面积:(平方米),
小圆柱侧面积:(平方米),
这个物体的表面积:(平方米);
答:这个物体的表面积是32.97平方米.
6.解:表面积:
,
,
,
(平方厘米);
体积:
,
,
,
(立方厘米);
答:它的表面积是2942平方厘米,体积是11140立方厘米.
7.解:
(立方厘米),
答:图中物体的体积是75.36立方厘米.
二、解决问题
1.解:(1),
,
(厘米),
面积:,
,
(平方厘米);
答:扎这个盒子至少用去塑料绳545厘米,在它的整个侧面贴上商标和说明,这部分的面积是2355平方厘米.
2.解:需要抹水泥的面积是:
,
,
,
(平方米),
(千克),
答:大约要用水泥424千克.
3.解:5厘米米,
(平方米);
答:做100节这样的水管至少需要37.68平方米的铁皮.
4.解:,
,
,
(平方厘米),
答:这个圆柱体的侧面积是452.16平方厘米.
5.解:(1)(平方米)
答:这个大棚的种植面积是32平方米.
(2)
(平方米)
答:覆盖在这个大棚上的塑料薄膜约有53.38平方米.
6.解:(厘米)
答:乙容器中的水深4厘米.
7.解:边上的高:
如图:
(厘米)
(立方厘米)
答:以为轴旋转一周形成的立体图形的体积是241.152立方厘米.
8.解:如下图:
(立方厘米),
答:这个立体图形的体积是87.92立方厘米.
9.解:(立方厘米)
(厘米)
答:这个圆锥形铁块的高大约是4.89厘米.
10.解:容器水下降的体积:
(立方厘米);
圆锥的底面积:
(平方厘米);
答:这个圆锥体的底面积是18.84平方厘米.
11.解:圆锥和圆柱的体积和:
(立方厘米);
(立方厘米),
答:圆锥体的体积是250立方厘米.
12.解:(厘米),
(立方厘米),
答:瓶内酸奶体积是25.92立方厘米.
13.解:
(厘米)
答:这时乙杯中的水位上升了4.5厘米.
14.解:圆形容器的底面积:
(平方厘米);
溢出水的体积,即放入容器的圆柱的体积:
,
,
(毫升);
圆柱体的体积是:
,
,
(立方厘米);
答:圆柱体的体积是25立方厘米.
15.解:根据题意画示意图如下:
解:
毫升
答:容器的容积是多少毫升660毫升.
16.解:
(立方厘米)
答:氧气泵的体积是5760立方厘米.
17.解:
(平方厘米);
(立方厘米);
答:这个零件的表面积是28.56平方厘米,体积是14.28立方厘米.
18.解:根据题意得
所以半径是2厘米.
(厘米)
(立方厘米)
答:这块橡皮泥的体积是75.36立方厘米.
19.解:圆锥的底面直径:
(厘米);
圆锥的体积:
(立方厘米),
答:这个圆锥的体积是157立方厘米.
20.解:,
,
(立方厘米),
答:拼成的大圆柱的体积是84.78立方厘米.
21.解:底面直径:(厘米),
(平方厘米),
答:表面积增加了224平方厘米.
22.解:圆柱的底面积:(平方厘米),
底面半径的平方:,
因为2的平方是4,所以圆柱的底面半径是2厘米,
圆柱的高:(厘米),
体积:,
,
(立方厘米),
答:这个圆柱的体积是62.8立方厘米.
23.解:底面半径是:(厘米)
底面积是:(平方厘米)
表面积是:
(平方厘米)
体积是:
(立方厘米)
答:这个长方体的底面积是28.26平方厘米,表面积是304.92平方厘米,体积是282.6立方厘米.
24.解:(立方分米)
答:削去部分的体积是35.2立方分米.
25.解:
.
答:这个圆锥体与原来正方体的体积比是.
26.解:24平方分米平方厘米
(厘米)
(立方厘米)
答:这个圆锥的体积是2512立方厘米.
27.解:
(立方分米)
答:这个圆锥形铅块的体积是81立方分米.
28.
(立方厘米);
答:这时甲水桶里有水1808.64立方厘米.
29.解:设圆钢的高为厘米,
圆钢体积
水桶底面积
因为下降的水的体积水面上圆钢的体积
,
,
,
,
,
圆钢体积(立方厘米).
答:这段圆钢的体积是1413立方厘米.
30.解:设圆锥形铁块的高是厘米
,
,
;
答:圆锥形铁块的高是60厘米.
31.解:
(平方厘米)
(厘米)
答:圆锥的高是12厘米.
32.解:放入等底等高的一根圆柱形钢材和一个圆锥以后,水面上升10厘米,
增加体积:(立方厘米),
由圆柱体和圆锥体体积公式知:等低等高的圆柱体积是圆锥体积的3倍,
设圆锥体体积为,则圆柱体体积为,
,
,
;
答:圆锥的体积是100立方厘米.
33.解:(平方厘米)
设圆柱底面半径为厘米
因为
所以
(厘米)
(立方厘米)
答:体积减小50.24立方厘米.
34.解:高6厘米的圆锥容器中水倒入等底的圆柱容器中高是(厘米)
(厘米),
答:如果将这个容器倒过来,这时水面距底部的高度是6厘米.
