六年级数学下册试题 一课一练《图形与几何-图形的运动》人教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《图形与几何-图形的运动》人教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 14:10:23 | ||
图片预览

文档简介
《图形与几何-图形的运动》
一、选择题
1.小红在镜子里看到墙上的挂钟如图所示,请问第 个时间最接近.
A.
B.
C.
D.
2.下面图形不是轴对称图形的是
A.
B.
C.
3.下列平面图形中,对称轴数量最多的是
A.圆
B.半圆
C.正方形
D.长方形
4.下列四个图形,按对称轴的条数从多到少依次排列,顺序正确的是
A.
B.
C.
D.
5.小明从镜子里看到镜子对面的电子钟的像如图所示,实际时间是
A.
B.
C.
D.
6.小明去学校,从家出发向东行200米,右转,直行200米,接着右转,直行200米到学校,学校在小明家的 边,距小明家直线距离 米.
A.东,200
B.南,200
C.西,400
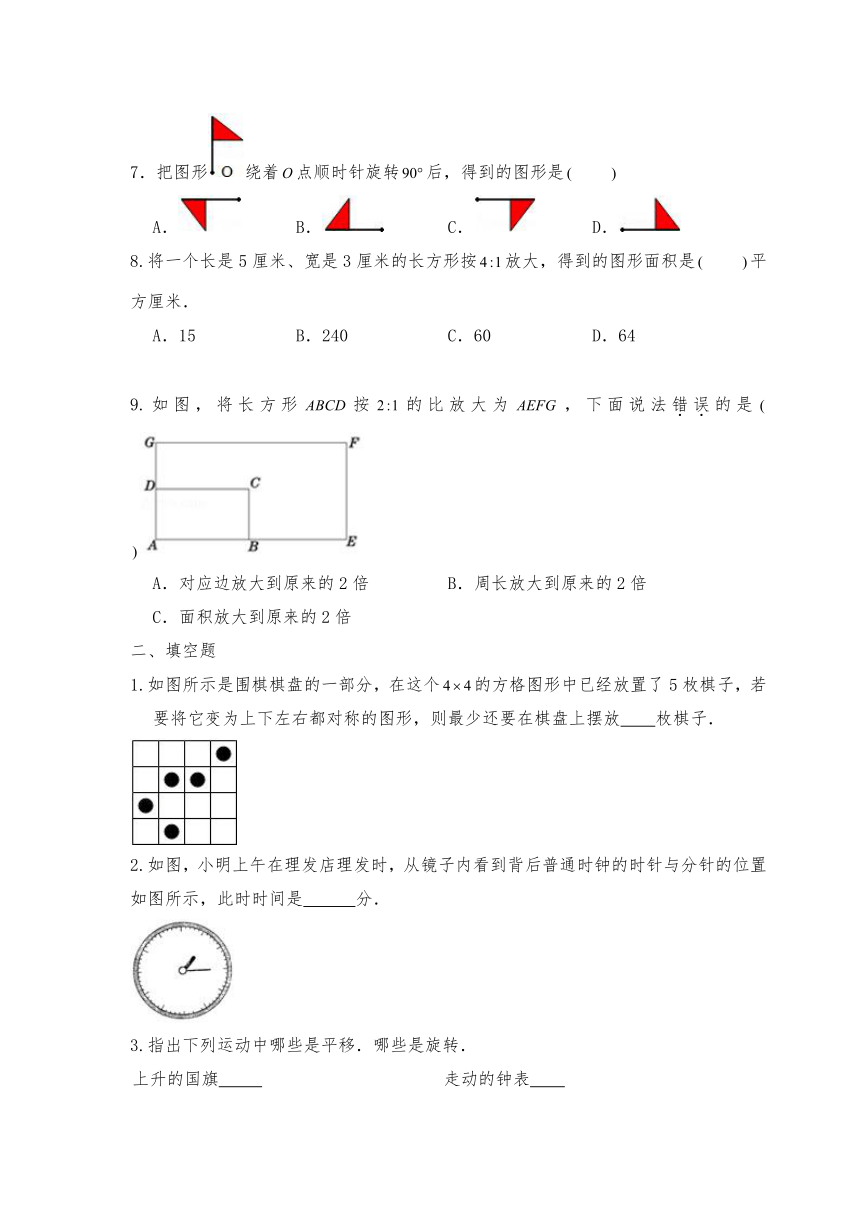
7.把图形绕着点顺时针旋转后,得到的图形是
A.
B.
C.
D.
8.将一个长是5厘米、宽是3厘米的长方形按放大,得到的图形面积是 平方厘米.
A.15
B.240
C.60
D.64
9.如图,将长方形按的比放大为,下面说法错误的是
A.对应边放大到原来的2倍
B.周长放大到原来的2倍
C.面积放大到原来的2倍
二、填空题
1.如图所示是围棋棋盘的一部分,在这个的方格图形中已经放置了5枚棋子,若要将它变为上下左右都对称的图形,则最少还要在棋盘上摆放 枚棋子.
2.如图,小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是
分.
3.指出下列运动中哪些是平移.哪些是旋转.
上升的国旗
走动的钟表
风车的转动
电梯的运动
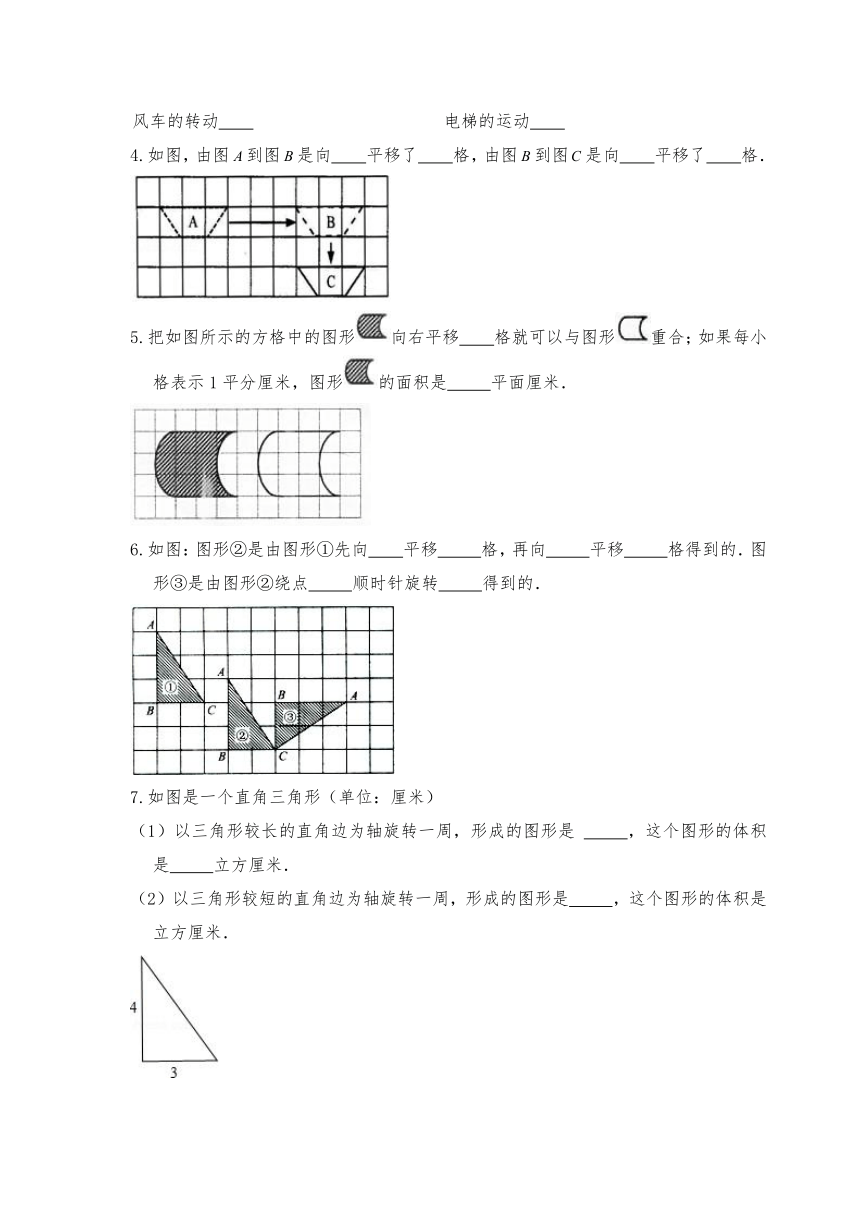
4.如图,由图到图是向 平移了 格,由图到图是向 平移了 格.
5.把如图所示的方格中的图形向右平移 格就可以与图形重合;如果每小格表示1平分厘米,图形的面积是
平面厘米.
6.如图:图形②是由图形①先向 平移
格,再向
平移
格得到的.图形③是由图形②绕点
顺时针旋转
得到的.
7.如图是一个直角三角形(单位:厘米)
(1)以三角形较长的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
8.一个三角形底是,高,把它按缩小后得到的三角形的面积是
.
9.一个半径是4厘米的圆,按的比放大后,放大后的圆的面积是 ;如果按
的比缩小后,圆的面积是3.14平方厘米.
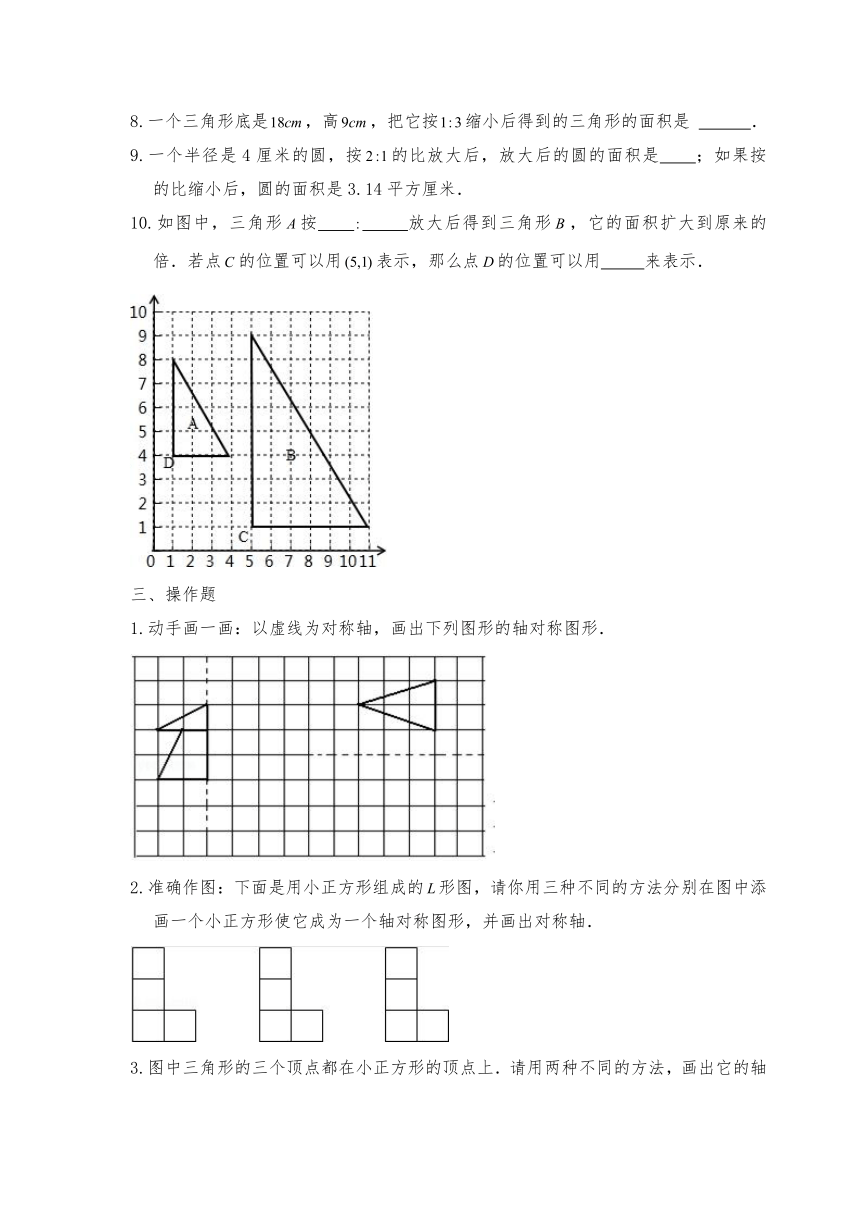
10.如图中,三角形按
放大后得到三角形,它的面积扩大到原来的
倍.若点的位置可以用表示,那么点的位置可以用
来表示.
三、操作题
1.动手画一画:以虚线为对称轴,画出下列图形的轴对称图形.
2.准确作图:下面是用小正方形组成的形图,请你用三种不同的方法分别在图中添画一个小正方形使它成为一个轴对称图形,并画出对称轴.
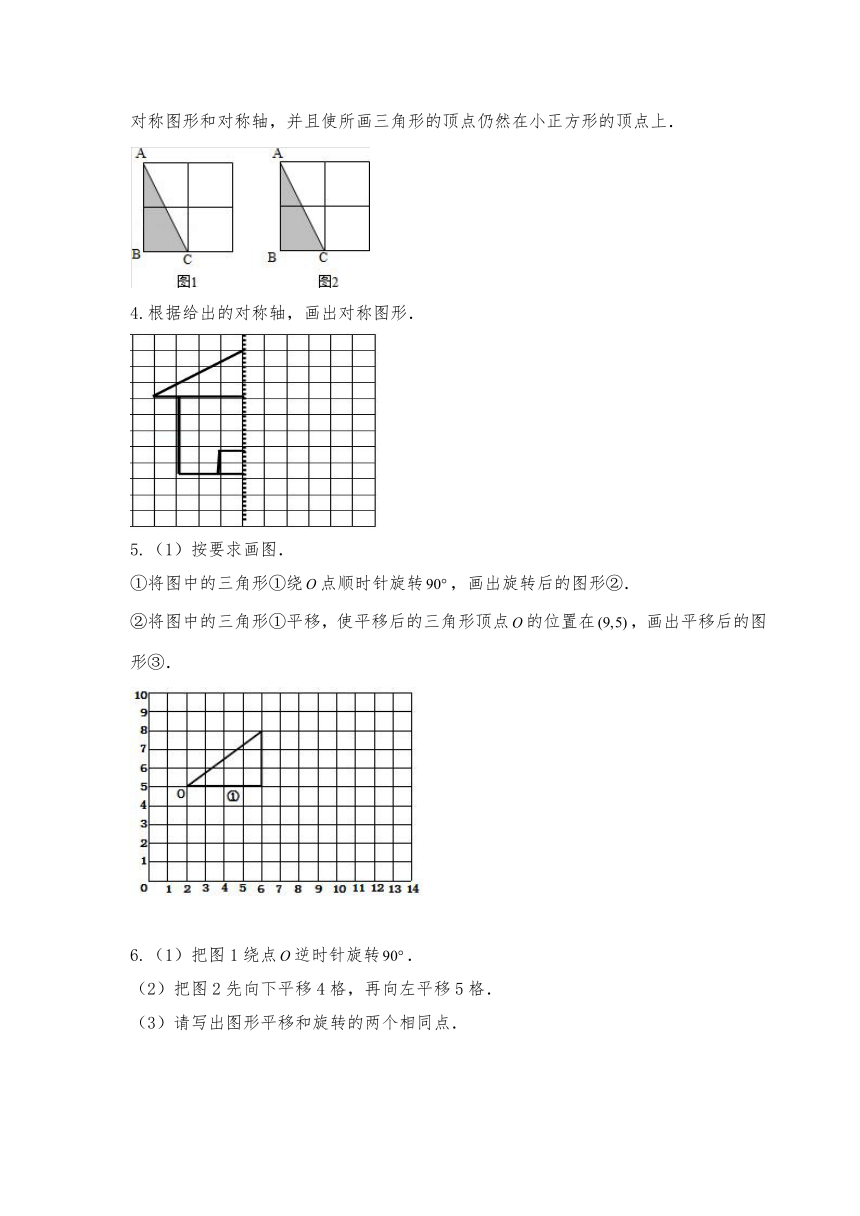
3.图中三角形的三个顶点都在小正方形的顶点上.请用两种不同的方法,画出它的轴对称图形和对称轴,并且使所画三角形的顶点仍然在小正方形的顶点上.
4.根据给出的对称轴,画出对称图形.
5.(1)按要求画图.
①将图中的三角形①绕点顺时针旋转,画出旋转后的图形②.
②将图中的三角形①平移,使平移后的三角形顶点的位置在,画出平移后的图形③.
6.(1)把图1绕点逆时针旋转.
(2)把图2先向下平移4格,再向左平移5格.
(3)请写出图形平移和旋转的两个相同点.
7.画一画(如图)
(1)画出图形绕点顺时针旋转后的图形.
(2)画出图形向右平移4格,再向下平移1格后的图形.
8.按要求画出图形.
(1)把小旗子向右平移6格.
(2)把小旗绕点逆时针旋转.
9.画一画.
(1)把三角形绕点逆时针旋转.
(2)把梯形向下平移3格.
10.把方格纸中的三角形按的比缩小,把平行四边形按的比放大.
11.如图
(1)按的比画出三角形变化后的图形.
(2)按的比画出圆变化后的图形,并与原来的圆组成轴对称图形.
(3)按的比画出平行四边形变化后的图形,
12.将左图按放大,将右图按缩小.
(1)三角形放大后的斜边与放大前斜边的比是:
.
(2)如果把圆按的比放大,那么放大后的面积与放大前面积的比是: .
13.
①按的比画出直角三角形缩小后的图形,使其直角顶点在处.
②将直角三角形绕点顺时针方向旋转,画出旋转后的图形.
14.下列方格图中,每小格为边长的小正方形.
(1)将上图按的比例画在右边.
(2)计算原图的周长与面积.
15.在下面的方格纸上画.
(1)画出三角形绕点顺时针旋转后的图形.
(2)画出圆向右平移5格后的图形.
(3)画出长方形按放大后的图形.
16.做一做,画一画
(1)画出图形的另一半,使它成为一个以直线为对称轴的对称图形.
(2)画出把图形向右平移6格后得到的图形.
(3)画出把图形绕点顺时针旋转后得到的图形.
(4)用数对表示点的位置是 .
17.按要求画画、填填.
(1)在长方形中画一个最大的圆,在这个长方形中一共可以画 个这样的圆.
(2)把长方形绕点顺时针旋转.
(3)在上图中,按的比画出长方形缩小后的图形.
(4)运用所学知识,在图中画出点的位置,再连接和,使三角形成为一个等边三角形.如果上图每个小方格的边长表示1厘米,那么点0的位置在点的 偏 方向 厘米处.
18.描点与画图.
(1)把平行四边形向下平移5格.
(2)图中点的位置用数对表示是 , .把梯形绕点逆时针旋转,画出旋转后的图形.
(3)把三角形按的比放大.
(4)画一个周长是的长方形,长与宽的比是.(图中每个小方格表示
19.(1)画出小旗图绕点逆时针旋转后的图形.
(2)以点为圆心,按的比画出圆放大后的图形.放大前和放大后圆的面积比是
.
(3)图中每个小方格的边长都表示1厘米.已知三角形是一个等边三角形,那么点在点的 偏
方向 厘米处.
20.按要求完成下面各题.
(1)画出四边形向右平移6格后的图形.再画出将四边形按缩小后的图形.
(2)画出把三角形绕点顺时针旋转后的图形.旋转后三角形的面积是
.
(3)用数对表示位置,三角形的顶点在旋转前位于 , ,旋转后位于 , .
(4)三角形是一个轴对称图形的一半,请画出这个轴对称图形的另一半.
21.按要求在下面方格纸上画图形.(每个小方格表示1平方厘米)
(1)按的比画出三角形放大后的图形.
(2)以为圆心,画一个直径6厘米的圆.
(3)画出房子图的另一半,使它成为一个轴对称图形.
(4)将平行四边形绕点逆时针方向旋转,画出旋转后的图形.
(5)画一个上底3厘米、下底5厘米,面积是16平方厘米的等腰梯形.
22.
(1)把长方形按的比缩小,画出缩小后的图形.
(2)把缩小后的长方形平移,与图中的圆组成一个轴对称图形.
(3)把三角形绕点按逆时针方向连续旋转3次,每次都旋转,画出最后的图形.
答案
一、选择题
1..2..3..4..5..6..7..8..9..
二、填空题
1.11.
2.10时45.
3.平移,旋转,旋转,平移.
4.右,6,下,2.
5.5,9.
6.右(下,3(或,下(右,2(或,点,.
7.高为4厘米底面半径为3厘米的圆锥,37.68;高为3厘米底面半径为4厘米的圆锥,50.24.
8.9平方厘米.
200.96平方厘米;.
10.2,1,4,.
三、操作题
1.解:
2.解:用三种不同的方法分别在图中添画一个小正方形使它成为一个轴对称图形,并画出对称轴.
3.解:
4.解:
5.解:根据分析可得,
6.解:(1)把图1绕点逆时针旋转900(图中红色部分).
(2)把图2先向下平移4格(图中灰色部分),再向左平移5格(图中绿色部分).
(3)图形平移和旋转的两个相同点:形状相同;大小不变.
7.解:(1)画出图形绕点顺时针旋转后的图形(图中红色部分)
(2)画出图形向右平移4格(图中灰色部分),再向下平移1格后的图形(图中绿色部分)
8.解:(1)把小旗子向右平移6格(图中红色部分).
(2)把小旗绕点逆时针旋转(图中绿色部分).
9.解:(1)把三角形绕点逆时针旋转.
(2)把梯形向下平移3格.
作图如下:
解:如图所示:
11.解:(1)按的比画出三角形变化后的图形(图中红色部分).
(2)按的比画出圆变化后的图形,并与原来的圆组成轴对称图形(图中绿色部分).
(3)按的比画出平行四边形变化后的图形(图中蓝色部分、红色虚线为对称轴).
12.解:(1)把三角形按放大,其放大后的各边与原来边的比都是,所以,三角形放大后的斜边与放大前斜边的比是:.
(2)圆按扩大,放大后的半径与放大前半径的比为,放大后的面积与放大前面积的比.
故答案为:;.
13.解:据分析画图如下:
14.解:(1)画图如下:
(2)周长:
(厘米)
面积:
(平方厘米)
答:图形的周长是16.28厘米,面积是12.28平方厘米.
15.解:(1)画出三角形绕点顺时针旋转后的图形(图中红色部分).
(2)画出圆向右平移5格后的图形(图中绿色部分).
(3)画出长方形按放大后的图形(图中蓝色部分).
16.解:(1)画出图形的另一半,使它成为一个以直线为对称轴的对称图形.
(2)画出把图形向右平移6格后得到的图形.
(3)画出把图形绕点顺时针旋转后得到的图形.
(4)用数对表示点的位置是.
17.解:如图:
(1)在长方形中画一个最大的圆,
以或为圆心,1为半径作圆.
答:这个长方形中一共可以画
2个这样的圆.
长方形绕点顺时针旋转后的图形如图.
(3)
按的比画出长方形缩小后的图形如图.
(4)如图三角形为等边三角形,如果上图每个小方格的边长表示1厘米,那么点0的位置在点的
东偏
南方向
1.5厘米处.
故答案为:2;东;南60;1.5.
18.解:(1)作图如下:
(2)的位置用数对表示是.
作图如下:
(3)(厘米),
作图如下:
(4)
作图如下:
(厘米),
,
(厘米),
(厘米),
故答案为:13、6.
19.解:(1)画出小旗图绕点逆时针旋转后的图形(图中红色部分);
(2)以点为圆心,按的比画出圆放大后的图形(图中绿色部分).
放大前和放大后圆的面积比是.
(3)(厘米)
答:点在点的东偏北方向3厘米处.
故答案为:1,4;东,北60,3.
20.解:(1)画出四边形向右平移6格后的图形(下图红色部分);再画出将四边形按缩小后的图形(下图蓝色部分)
(2)画出把三角形绕点顺时针旋转后的图形(下图黄色部分);
(平方厘米)
旋转后三角形的面积是.
(3)用数对表示位置,三角形的顶点在旋转前位于,旋转后位于.
(3)三角形是一个轴对称图形的一半,请画出这个轴对称图形的另一半(下图绿色部分).
故答案为:3;7,3,10,6.
21.解:(1)三角形按放大后如图所示.
(2)(厘米)
所以,所画圆如图.
(3)图形的另一半如图所示.
(4)平行四边形绕点逆时针旋转后的图形如图.
(5)
(厘米)
梯形如图.
22.解:作图如下:
一、选择题
1.小红在镜子里看到墙上的挂钟如图所示,请问第 个时间最接近.
A.
B.
C.
D.
2.下面图形不是轴对称图形的是
A.
B.
C.
3.下列平面图形中,对称轴数量最多的是
A.圆
B.半圆
C.正方形
D.长方形
4.下列四个图形,按对称轴的条数从多到少依次排列,顺序正确的是
A.
B.
C.
D.
5.小明从镜子里看到镜子对面的电子钟的像如图所示,实际时间是
A.
B.
C.
D.
6.小明去学校,从家出发向东行200米,右转,直行200米,接着右转,直行200米到学校,学校在小明家的 边,距小明家直线距离 米.
A.东,200
B.南,200
C.西,400
7.把图形绕着点顺时针旋转后,得到的图形是
A.
B.
C.
D.
8.将一个长是5厘米、宽是3厘米的长方形按放大,得到的图形面积是 平方厘米.
A.15
B.240
C.60
D.64
9.如图,将长方形按的比放大为,下面说法错误的是
A.对应边放大到原来的2倍
B.周长放大到原来的2倍
C.面积放大到原来的2倍
二、填空题
1.如图所示是围棋棋盘的一部分,在这个的方格图形中已经放置了5枚棋子,若要将它变为上下左右都对称的图形,则最少还要在棋盘上摆放 枚棋子.
2.如图,小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是
分.
3.指出下列运动中哪些是平移.哪些是旋转.
上升的国旗
走动的钟表
风车的转动
电梯的运动
4.如图,由图到图是向 平移了 格,由图到图是向 平移了 格.
5.把如图所示的方格中的图形向右平移 格就可以与图形重合;如果每小格表示1平分厘米,图形的面积是
平面厘米.
6.如图:图形②是由图形①先向 平移
格,再向
平移
格得到的.图形③是由图形②绕点
顺时针旋转
得到的.
7.如图是一个直角三角形(单位:厘米)
(1)以三角形较长的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
8.一个三角形底是,高,把它按缩小后得到的三角形的面积是
.
9.一个半径是4厘米的圆,按的比放大后,放大后的圆的面积是 ;如果按
的比缩小后,圆的面积是3.14平方厘米.
10.如图中,三角形按
放大后得到三角形,它的面积扩大到原来的
倍.若点的位置可以用表示,那么点的位置可以用
来表示.
三、操作题
1.动手画一画:以虚线为对称轴,画出下列图形的轴对称图形.
2.准确作图:下面是用小正方形组成的形图,请你用三种不同的方法分别在图中添画一个小正方形使它成为一个轴对称图形,并画出对称轴.
3.图中三角形的三个顶点都在小正方形的顶点上.请用两种不同的方法,画出它的轴对称图形和对称轴,并且使所画三角形的顶点仍然在小正方形的顶点上.
4.根据给出的对称轴,画出对称图形.
5.(1)按要求画图.
①将图中的三角形①绕点顺时针旋转,画出旋转后的图形②.
②将图中的三角形①平移,使平移后的三角形顶点的位置在,画出平移后的图形③.
6.(1)把图1绕点逆时针旋转.
(2)把图2先向下平移4格,再向左平移5格.
(3)请写出图形平移和旋转的两个相同点.
7.画一画(如图)
(1)画出图形绕点顺时针旋转后的图形.
(2)画出图形向右平移4格,再向下平移1格后的图形.
8.按要求画出图形.
(1)把小旗子向右平移6格.
(2)把小旗绕点逆时针旋转.
9.画一画.
(1)把三角形绕点逆时针旋转.
(2)把梯形向下平移3格.
10.把方格纸中的三角形按的比缩小,把平行四边形按的比放大.
11.如图
(1)按的比画出三角形变化后的图形.
(2)按的比画出圆变化后的图形,并与原来的圆组成轴对称图形.
(3)按的比画出平行四边形变化后的图形,
12.将左图按放大,将右图按缩小.
(1)三角形放大后的斜边与放大前斜边的比是:
.
(2)如果把圆按的比放大,那么放大后的面积与放大前面积的比是: .
13.
①按的比画出直角三角形缩小后的图形,使其直角顶点在处.
②将直角三角形绕点顺时针方向旋转,画出旋转后的图形.
14.下列方格图中,每小格为边长的小正方形.
(1)将上图按的比例画在右边.
(2)计算原图的周长与面积.
15.在下面的方格纸上画.
(1)画出三角形绕点顺时针旋转后的图形.
(2)画出圆向右平移5格后的图形.
(3)画出长方形按放大后的图形.
16.做一做,画一画
(1)画出图形的另一半,使它成为一个以直线为对称轴的对称图形.
(2)画出把图形向右平移6格后得到的图形.
(3)画出把图形绕点顺时针旋转后得到的图形.
(4)用数对表示点的位置是 .
17.按要求画画、填填.
(1)在长方形中画一个最大的圆,在这个长方形中一共可以画 个这样的圆.
(2)把长方形绕点顺时针旋转.
(3)在上图中,按的比画出长方形缩小后的图形.
(4)运用所学知识,在图中画出点的位置,再连接和,使三角形成为一个等边三角形.如果上图每个小方格的边长表示1厘米,那么点0的位置在点的 偏 方向 厘米处.
18.描点与画图.
(1)把平行四边形向下平移5格.
(2)图中点的位置用数对表示是 , .把梯形绕点逆时针旋转,画出旋转后的图形.
(3)把三角形按的比放大.
(4)画一个周长是的长方形,长与宽的比是.(图中每个小方格表示
19.(1)画出小旗图绕点逆时针旋转后的图形.
(2)以点为圆心,按的比画出圆放大后的图形.放大前和放大后圆的面积比是
.
(3)图中每个小方格的边长都表示1厘米.已知三角形是一个等边三角形,那么点在点的 偏
方向 厘米处.
20.按要求完成下面各题.
(1)画出四边形向右平移6格后的图形.再画出将四边形按缩小后的图形.
(2)画出把三角形绕点顺时针旋转后的图形.旋转后三角形的面积是
.
(3)用数对表示位置,三角形的顶点在旋转前位于 , ,旋转后位于 , .
(4)三角形是一个轴对称图形的一半,请画出这个轴对称图形的另一半.
21.按要求在下面方格纸上画图形.(每个小方格表示1平方厘米)
(1)按的比画出三角形放大后的图形.
(2)以为圆心,画一个直径6厘米的圆.
(3)画出房子图的另一半,使它成为一个轴对称图形.
(4)将平行四边形绕点逆时针方向旋转,画出旋转后的图形.
(5)画一个上底3厘米、下底5厘米,面积是16平方厘米的等腰梯形.
22.
(1)把长方形按的比缩小,画出缩小后的图形.
(2)把缩小后的长方形平移,与图中的圆组成一个轴对称图形.
(3)把三角形绕点按逆时针方向连续旋转3次,每次都旋转,画出最后的图形.
答案
一、选择题
1..2..3..4..5..6..7..8..9..
二、填空题
1.11.
2.10时45.
3.平移,旋转,旋转,平移.
4.右,6,下,2.
5.5,9.
6.右(下,3(或,下(右,2(或,点,.
7.高为4厘米底面半径为3厘米的圆锥,37.68;高为3厘米底面半径为4厘米的圆锥,50.24.
8.9平方厘米.
200.96平方厘米;.
10.2,1,4,.
三、操作题
1.解:
2.解:用三种不同的方法分别在图中添画一个小正方形使它成为一个轴对称图形,并画出对称轴.
3.解:
4.解:
5.解:根据分析可得,
6.解:(1)把图1绕点逆时针旋转900(图中红色部分).
(2)把图2先向下平移4格(图中灰色部分),再向左平移5格(图中绿色部分).
(3)图形平移和旋转的两个相同点:形状相同;大小不变.
7.解:(1)画出图形绕点顺时针旋转后的图形(图中红色部分)
(2)画出图形向右平移4格(图中灰色部分),再向下平移1格后的图形(图中绿色部分)
8.解:(1)把小旗子向右平移6格(图中红色部分).
(2)把小旗绕点逆时针旋转(图中绿色部分).
9.解:(1)把三角形绕点逆时针旋转.
(2)把梯形向下平移3格.
作图如下:
解:如图所示:
11.解:(1)按的比画出三角形变化后的图形(图中红色部分).
(2)按的比画出圆变化后的图形,并与原来的圆组成轴对称图形(图中绿色部分).
(3)按的比画出平行四边形变化后的图形(图中蓝色部分、红色虚线为对称轴).
12.解:(1)把三角形按放大,其放大后的各边与原来边的比都是,所以,三角形放大后的斜边与放大前斜边的比是:.
(2)圆按扩大,放大后的半径与放大前半径的比为,放大后的面积与放大前面积的比.
故答案为:;.
13.解:据分析画图如下:
14.解:(1)画图如下:
(2)周长:
(厘米)
面积:
(平方厘米)
答:图形的周长是16.28厘米,面积是12.28平方厘米.
15.解:(1)画出三角形绕点顺时针旋转后的图形(图中红色部分).
(2)画出圆向右平移5格后的图形(图中绿色部分).
(3)画出长方形按放大后的图形(图中蓝色部分).
16.解:(1)画出图形的另一半,使它成为一个以直线为对称轴的对称图形.
(2)画出把图形向右平移6格后得到的图形.
(3)画出把图形绕点顺时针旋转后得到的图形.
(4)用数对表示点的位置是.
17.解:如图:
(1)在长方形中画一个最大的圆,
以或为圆心,1为半径作圆.
答:这个长方形中一共可以画
2个这样的圆.
长方形绕点顺时针旋转后的图形如图.
(3)
按的比画出长方形缩小后的图形如图.
(4)如图三角形为等边三角形,如果上图每个小方格的边长表示1厘米,那么点0的位置在点的
东偏
南方向
1.5厘米处.
故答案为:2;东;南60;1.5.
18.解:(1)作图如下:
(2)的位置用数对表示是.
作图如下:
(3)(厘米),
作图如下:
(4)
作图如下:
(厘米),
,
(厘米),
(厘米),
故答案为:13、6.
19.解:(1)画出小旗图绕点逆时针旋转后的图形(图中红色部分);
(2)以点为圆心,按的比画出圆放大后的图形(图中绿色部分).
放大前和放大后圆的面积比是.
(3)(厘米)
答:点在点的东偏北方向3厘米处.
故答案为:1,4;东,北60,3.
20.解:(1)画出四边形向右平移6格后的图形(下图红色部分);再画出将四边形按缩小后的图形(下图蓝色部分)
(2)画出把三角形绕点顺时针旋转后的图形(下图黄色部分);
(平方厘米)
旋转后三角形的面积是.
(3)用数对表示位置,三角形的顶点在旋转前位于,旋转后位于.
(3)三角形是一个轴对称图形的一半,请画出这个轴对称图形的另一半(下图绿色部分).
故答案为:3;7,3,10,6.
21.解:(1)三角形按放大后如图所示.
(2)(厘米)
所以,所画圆如图.
(3)图形的另一半如图所示.
(4)平行四边形绕点逆时针旋转后的图形如图.
(5)
(厘米)
梯形如图.
22.解:作图如下:
