鲁教版六年级数学下册第九章 变量之间的关系 单元测试题(Word版含答案)
文档属性
| 名称 | 鲁教版六年级数学下册第九章 变量之间的关系 单元测试题(Word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 22:28:57 | ||
图片预览


文档简介
鲁教版六年级数学下册第九章
变量之间的关系
单元测试题
一、选择题
弹簧挂重物会伸长,测得弹簧长度最长为20cm,与所挂物体重量间有下面的关系.
x
0
1
2
3
4
y
8
9
10
下列说法不正确的是
A.
x与y都是变量,x是自变量,y是因变量
B.
所挂物体为6kg,弹簧长度为11cm
C.
物体每增加1kg,弹簧长度就增加
D.
挂30kg物体时一定比原长增加15cm
某汽车油箱中盛有油100L,装满货物行驶的过程中每小时耗油8L,则油箱中的剩油量与时间之间的关系式是
A.
B.
C.
D.
甲、乙两人在100米赛跑中,路程与时间的关系如图所示,根据图象,下列结论错误的是
A.
甲比乙先到达终点
B.
甲、乙速度相差
C.
甲的速度为
D.
乙跑完全程需12s
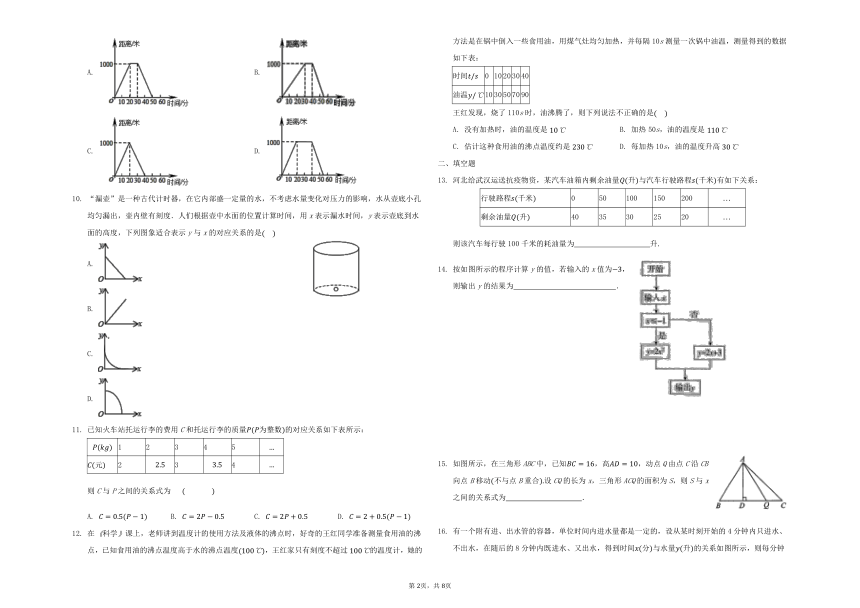
一面冉冉升起的旗子高度与时间的关系可以用来近似地刻画的是
A.
B.
C.
D.
张大伯出去散步,从家走了20min,到了一个离家900m的阅报亭,看了10min报纸后,用了15min返回到家,如图图象中能表示张大伯离家时间与距离之间关系的是?
?
A.
B.
C.
D.
变量x与y之间的关系是,当时,自变量x的值是
A.
13
B.
5
C.
2
D.
如图所示,在长方形ABCD中,,,P是CD上的动点,且不与点C,D重合,设,梯形ABCP的面积为y,则y与x之间的关系式和自变量的取值范围分别是
A.
;
B.
;
C.
;
D.
;
某数学兴趣小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下表,下列说法错误的是
温度
0
10
20
30
声速
318
324
330
336
342
348
A.
在这个变化中自变量是温度,因变量是声速
B.
当温度每升高,声速增加
C.
当空气温度为,的时间声音可以传播
D.
温度越高声速越快
小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系
A.
B.
C.
D.
“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用x表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是
A.
B.
C.
D.
已知火车站托运行李的费用C和托运行李的质量为整数的对应关系如下表所示:
1
2
3
4
5
元
2
3
4
则C与P之间的关系式为?
???
A.
B.
C.
D.
在科学课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度,王红家只有刻度不超过的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔10s测量一次锅中油温,测量得到的数据如下表:
时间
0
10
20
30
40
油温
10
30
50
70
90
王红发现,烧了110s时,油沸腾了,则下列说法不正确的是
A.
没有加热时,油的温度是
B.
加热50s,油的温度是
C.
估计这种食用油的沸点温度约是
D.
每加热10s,油的温度升高
二、填空题
河北给武汉运送抗疫物资,某汽车油箱内剩余油量升与汽车行驶路程千米有如下关系:
行驶路程千米
0
50
100
150
200
剩余油量升
40
35
30
25
20
则该汽车每行驶100千米的耗油量为??????????升
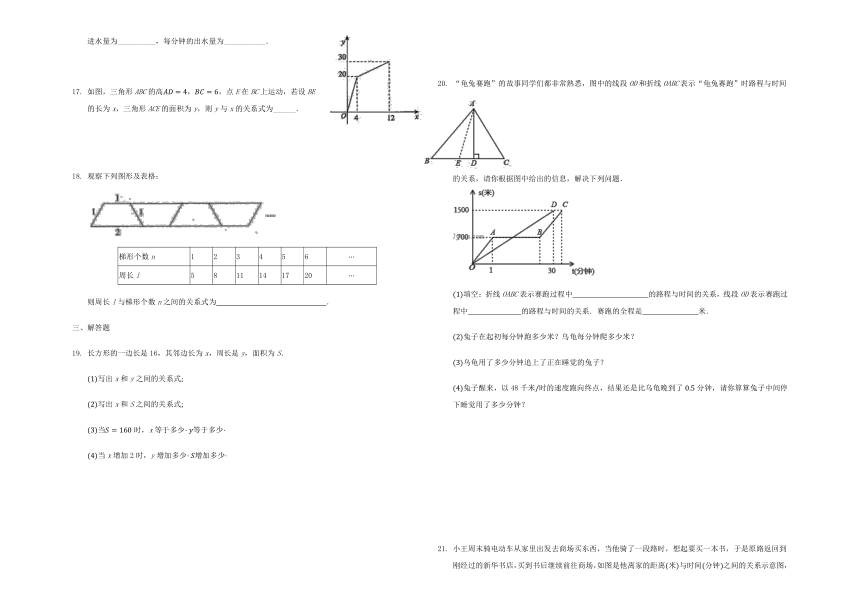
按如图所示的程序计算y的值,若输入的x值为,则输出y的结果为???????????
??.
如图所示,在三角形ABC中,已知,高,动点Q由点C沿CB向点B移动不与点B重合设CQ的长为x,三角形ACQ的面积为S,则S与x之间的关系式为??????????.
有一个附有进、出水管的容器,单位时间内进水量都是一定的,设从某时刻开始的4分钟内只进水、不出水,在随后的8分钟内既进水、又出水,得到时间分与水量升的关系如图所示,则每分钟进水量为__________,每分钟的出水量为___________.
如图,三角形ABC的高,,点E在BC上运动,若设BE的长为x,三角形ACE的面积为y,则y与x的关系式为______.
观察下列图形及表格:
梯形个数n
1
2
3
4
5
6
周长l
5
8
11
14
17
20
则周长l与梯形个数n之间的关系式为????????????
??.
三、解答题
长方形的一边长是16,其邻边长为x,周长是y,面积为S.
写出x和y之间的关系式
写出x和S之间的关系式
当时,x等于多少等于多少
当x增加2时,y增加多少增加多少
“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
填空:折线OABC表示赛跑过程中??????????的路程与时间的关系,线段OD表示赛跑过程中?
?
?
?
?的路程与时间的关系.赛跑的全程是?
?
?
?
?米.
兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
乌龟用了多少分钟追上了正在睡觉的兔子?
兔子醒来,以48千米时的速度跑向终点,结果还是比乌龟晚到了分钟,请你算算兔子中间停下睡觉用了多少分钟?
小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离米与时间分钟之间的关系示意图,请根据图中提供的信息回答下列问题:
在此变化过程中,自变量是______,因变量是______.
小王在新华书店停留了多长时间?
买到书后,小王从新华书店到商场的骑车速度是多少?
已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如下关系:
底面半径
用铝量
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
当易拉罐底面半径为时,易拉罐需要的用铝量是多少?
根据表格中的数据,你认为易拉罐的底面半径为多少时比较合适?说说你的理由.
某软件公司开发了一种图书管理软件,前期投入开发广告宣传费用共50000元,且每出售一套软件,软件公司支付安装费200元.
写出总费用y元和出售套数x之间的关系式
若该套软件售价为700元,则该软件公司必须出售软件多少套及以上才能不亏本
答案和解析
1.【答案】D
【解析】分析
根据表格中的数据即可判断;
本题考查用表格反映变量间的关系,解题的关键是理解题意,掌握变量间的变化规律.
详解
解:
A.正确.x与y都是变量,x是自变量,y是因变量;
B.正确.所挂物体为6kg,弹簧长度为11cm;
C.正确.物体每增加1kg,弹簧长度就增加;
D.错误,弹簧长度最长为20cm;
故选D.
2.【答案】C
【解析】分析
根据油箱剩油量等于总油量减去消耗的油量列出关系式即可.
本题考查了用关系式表示变量间的关系,比较简单.
详解
解:由题意得,油箱剩油量.
故选C.
3.【答案】B
【解析】分析
通过图象可以看出甲乙两人从同一起点同时出发,路程都是100米,甲用时10秒,乙用时12秒,依次可判断甲乙的速度,从而解决问题.
本题主要考查了用图象反映变量间的关系,需要从图象分析出实际问题,解题的关键是理解横轴和纵轴表示的含义,转化为实际问题中的数据.
详解
解:通过图象可以看出甲乙两人从同一起点同时出发,路程都是100米,甲用时10秒,乙用时12秒,
所以甲比乙先到达终点,所以A结论正确,不符合题意;
甲的速度为,乙的速度为,所以B选项错误符合题意;
C和D选项结论均正确,不符合题意.
故选B.
4.【答案】D
【解析】分析
本题考查了用图象反映变量间的关系,解题的关键是了解两个变量之间的关系以及对生活中的现象的了解.
冉冉升起的旗子随着时间的推移高度慢慢增加,对照选项中的图象可作出正确的判断.
详解
解:旗子是匀速上升的,且开始时是拿在同学手中,
旗子随着时间的增加,其高度也在不断增大,
只有D选项图象符合.
故选D.
5.【答案】C
【解析】分析
要找出准确反映时间与距离之间对应关系的图象,需分析在不同阶段中距离随时间变化的情况.
本题考查的是用图象反映变量间的关系,根据题意,对照各选项中的图象即可做出正确的选择.
详解
解:张大伯在行走的过程中,分三个阶段:
第一个:0到20min,距离从0变到了900m,
第二个:中间看报的时间内距离没有变化,为水平线,时间为20min到30min,
第三个:后15min,即30min到45min之间,距离从900米变到了0米,
由此可判断出C选项正确,A、D的图象没有第二个阶段,而B的第二个阶段时长应是20min到30min.
故选C.
6.【答案】C
【解析】
【分析】
此题主要考查变量x与y之间的关系式,关键是掌握已知的关系式,给出因变量的值时,解方程求出相应的自变量的值即可.
直接把代入,解方程即可.
【解答】
解:当时,,
解得:.
故选C.
7.【答案】A
【解析】分析
本题考查了用关系式表示变量间的关系、自变量取值范围及梯形面积先确定梯形ABCP的上底、下底和高,代入数据即可得梯形ABCP的面积y与DP长x之间的关系式.
详解
解:由梯形面积公式知,,,,
,
即,
且不与点C,D重合
,
.
故选A.
8.【答案】C
【解析】略
9.【答案】D
【解析】解:根据题意,从20分钟到40分钟哥哥在书店里看书,离家距离没有变化,是一条平行于x轴的线段.
故选:D.
根据哥哥看了20分钟书后,用15分钟返家即可判断哥哥的离家时间与距离之间的关系.
本题考查函数的图象,解题的关键是正确将文字语言转化为图形语言,本题属于基础题型.
10.【答案】A
【解析】解:不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,x表示漏水时间,y表示壶底到水面的高度,
随x的增大而减小,符合函数图象,
故选:A.
根据题意,可知y随x的增大而减小,符合函数图象,从而可以解答本题.
本题考查函数图象,解答本题的关键是明确题意,利用数形结合的思想解答.
11.【答案】D
【解析】分析
本题考查了用关系式表示的变量间关系,通过表格找出P增加1,则对应的C增加是关键根据表格中的数据可以得到P增加1,则对应的C增加,据此即可求解.
详解
解:根据表可以得到P增加1,则对应的C增加,
则C与P的对应关系是:.
故选D.
12.【答案】D
【解析】分析
从表格可知:时,,即没有加热时,油的温度为;每增加10秒,温度上升,则时,油温度;秒时,温度.
本题考查自变量与因变量的关系;能够通过表格确定自变量与因变量的变化关系是解题的关键.
详解
解:从表格可知:时,,即没有加热时,油的温度为,A正确;
每增加10秒,温度上升,则50秒时,油温度,B正确,D错误;
110秒时,温度,C正确;
故选D.
13.【答案】10
【解析】由题表可得,该汽车每行驶100千米的耗油量为升,
故答案为10.
14.【答案】18
【解析】解:,
把代入,得,
故答案为18.
15.【答案】
【解析】
【分析】
本题考查了函数关系式,利用三角形的面积是解题关键.根据三角形的面积公式,可得答案.
【解答】
解:,,
,
故答案为.
16.【答案】5升;升
【解析】
【分析】
此题这样考查了一次函数的应用问题,解题时首先正确理解题意,接着利用函数的性质即可解决问题.根据图象和已知条件可以求出每分钟进水,出水各多少升.
【解答】
解:由图可知:4分钟时,进水20升,每分钟进水量为升,
根据图象知道:每分钟出水升;
故答案为5升;升.
17.【答案】
【解析】解:由线段的和差,得,
由三角形的面积,得
,
化简,得,
故答案为:.
根据线段的和差,可得CE的长,根据三角形的面积,可得答案.
本题考查了函数关系式,利用三角形的面积公式是解题关键.
18.【答案】
【解析】解:由表格数据找出规律或由图形找出答案.
19.【答案】解:由长方形的周长公式,得.
由长方形的面积公式,得.
当时,,.
当x增加2时,y增加4,S增加32.
【解析】略
20.【答案】兔子、乌龟、1500
解:兔子在起初每分钟跑米,乌龟每分钟爬米
解:,
乌龟用了14分钟追上了正在睡觉的兔子
解:千米时米分钟,
,
兔子中间停下睡觉用了分钟
【解析】
【分析】
本题考查的是函数图象有关知识.
根据点D实际意义知全程的距离;
根据点A实际意义知兔子起初速度,由点D实际意义可知乌龟的速度;
利用兔子睡觉前行驶的路程是700米,结合乌龟的速度求出所用的时间;
根据比乌龟晚到了分钟求出兔子走完全程的时间,再得出兔子醒来后奔跑所用时间,求解可得.
【解答】
解:乌龟是一直跑的而兔子中间有休息的时刻;
折线OABC表示赛跑过程中兔子的路程与时间的关系;
线段OD表示赛跑过程中乌龟的路程与时间的关系;
由图象可知:赛跑的路程为1500米;
故答案为兔子、乌龟、1500;
见答案;
见答案;
见答案.
21.【答案】时间?
距离
【解析】解:在此变化过程中,自变量是时间,因变量是距离.
故答案为:时间;距离;
分钟.
所以小王在新华书店停留了10分钟;
小王从新华书店到商场的路程为米,所用时间为分钟,
小王从新华书店到商场的骑车速度是:米分.
根据图象作答即可;
由函数图象可知,分钟的路程没变,所以小王在新华书店停留了10分钟;
小王从新华书店到商场的路程为米,所用时间为分钟,根据速度路程时间,即可解答.
本题主要考查了函数图象的读图能力,要理解横纵坐标表示的含义以及小王的运动过程是解题的关键.
22.【答案】解:反映了易拉罐的底面半径和用铝量的关系,
其中,易拉罐的底面半径为自变量,用铝量为因变量.
当底面半径为时,易拉罐需要的用铝量为.
易拉罐的底面半径为时比较合适,因为此时用铝量较少,成本低.
【解析】略
23.【答案】解:.
由题意,知,解得,即该软件公司必须出售软件100套及以上才能不亏本.
【解析】略
第4页,共8页
变量之间的关系
单元测试题
一、选择题
弹簧挂重物会伸长,测得弹簧长度最长为20cm,与所挂物体重量间有下面的关系.
x
0
1
2
3
4
y
8
9
10
下列说法不正确的是
A.
x与y都是变量,x是自变量,y是因变量
B.
所挂物体为6kg,弹簧长度为11cm
C.
物体每增加1kg,弹簧长度就增加
D.
挂30kg物体时一定比原长增加15cm
某汽车油箱中盛有油100L,装满货物行驶的过程中每小时耗油8L,则油箱中的剩油量与时间之间的关系式是
A.
B.
C.
D.
甲、乙两人在100米赛跑中,路程与时间的关系如图所示,根据图象,下列结论错误的是
A.
甲比乙先到达终点
B.
甲、乙速度相差
C.
甲的速度为
D.
乙跑完全程需12s
一面冉冉升起的旗子高度与时间的关系可以用来近似地刻画的是
A.
B.
C.
D.
张大伯出去散步,从家走了20min,到了一个离家900m的阅报亭,看了10min报纸后,用了15min返回到家,如图图象中能表示张大伯离家时间与距离之间关系的是?
?
A.
B.
C.
D.
变量x与y之间的关系是,当时,自变量x的值是
A.
13
B.
5
C.
2
D.
如图所示,在长方形ABCD中,,,P是CD上的动点,且不与点C,D重合,设,梯形ABCP的面积为y,则y与x之间的关系式和自变量的取值范围分别是
A.
;
B.
;
C.
;
D.
;
某数学兴趣小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下表,下列说法错误的是
温度
0
10
20
30
声速
318
324
330
336
342
348
A.
在这个变化中自变量是温度,因变量是声速
B.
当温度每升高,声速增加
C.
当空气温度为,的时间声音可以传播
D.
温度越高声速越快
小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系
A.
B.
C.
D.
“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用x表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是
A.
B.
C.
D.
已知火车站托运行李的费用C和托运行李的质量为整数的对应关系如下表所示:
1
2
3
4
5
元
2
3
4
则C与P之间的关系式为?
???
A.
B.
C.
D.
在科学课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度,王红家只有刻度不超过的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔10s测量一次锅中油温,测量得到的数据如下表:
时间
0
10
20
30
40
油温
10
30
50
70
90
王红发现,烧了110s时,油沸腾了,则下列说法不正确的是
A.
没有加热时,油的温度是
B.
加热50s,油的温度是
C.
估计这种食用油的沸点温度约是
D.
每加热10s,油的温度升高
二、填空题
河北给武汉运送抗疫物资,某汽车油箱内剩余油量升与汽车行驶路程千米有如下关系:
行驶路程千米
0
50
100
150
200
剩余油量升
40
35
30
25
20
则该汽车每行驶100千米的耗油量为??????????升
按如图所示的程序计算y的值,若输入的x值为,则输出y的结果为???????????
??.
如图所示,在三角形ABC中,已知,高,动点Q由点C沿CB向点B移动不与点B重合设CQ的长为x,三角形ACQ的面积为S,则S与x之间的关系式为??????????.
有一个附有进、出水管的容器,单位时间内进水量都是一定的,设从某时刻开始的4分钟内只进水、不出水,在随后的8分钟内既进水、又出水,得到时间分与水量升的关系如图所示,则每分钟进水量为__________,每分钟的出水量为___________.
如图,三角形ABC的高,,点E在BC上运动,若设BE的长为x,三角形ACE的面积为y,则y与x的关系式为______.
观察下列图形及表格:
梯形个数n
1
2
3
4
5
6
周长l
5
8
11
14
17
20
则周长l与梯形个数n之间的关系式为????????????
??.
三、解答题
长方形的一边长是16,其邻边长为x,周长是y,面积为S.
写出x和y之间的关系式
写出x和S之间的关系式
当时,x等于多少等于多少
当x增加2时,y增加多少增加多少
“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
填空:折线OABC表示赛跑过程中??????????的路程与时间的关系,线段OD表示赛跑过程中?
?
?
?
?的路程与时间的关系.赛跑的全程是?
?
?
?
?米.
兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
乌龟用了多少分钟追上了正在睡觉的兔子?
兔子醒来,以48千米时的速度跑向终点,结果还是比乌龟晚到了分钟,请你算算兔子中间停下睡觉用了多少分钟?
小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离米与时间分钟之间的关系示意图,请根据图中提供的信息回答下列问题:
在此变化过程中,自变量是______,因变量是______.
小王在新华书店停留了多长时间?
买到书后,小王从新华书店到商场的骑车速度是多少?
已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如下关系:
底面半径
用铝量
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
当易拉罐底面半径为时,易拉罐需要的用铝量是多少?
根据表格中的数据,你认为易拉罐的底面半径为多少时比较合适?说说你的理由.
某软件公司开发了一种图书管理软件,前期投入开发广告宣传费用共50000元,且每出售一套软件,软件公司支付安装费200元.
写出总费用y元和出售套数x之间的关系式
若该套软件售价为700元,则该软件公司必须出售软件多少套及以上才能不亏本
答案和解析
1.【答案】D
【解析】分析
根据表格中的数据即可判断;
本题考查用表格反映变量间的关系,解题的关键是理解题意,掌握变量间的变化规律.
详解
解:
A.正确.x与y都是变量,x是自变量,y是因变量;
B.正确.所挂物体为6kg,弹簧长度为11cm;
C.正确.物体每增加1kg,弹簧长度就增加;
D.错误,弹簧长度最长为20cm;
故选D.
2.【答案】C
【解析】分析
根据油箱剩油量等于总油量减去消耗的油量列出关系式即可.
本题考查了用关系式表示变量间的关系,比较简单.
详解
解:由题意得,油箱剩油量.
故选C.
3.【答案】B
【解析】分析
通过图象可以看出甲乙两人从同一起点同时出发,路程都是100米,甲用时10秒,乙用时12秒,依次可判断甲乙的速度,从而解决问题.
本题主要考查了用图象反映变量间的关系,需要从图象分析出实际问题,解题的关键是理解横轴和纵轴表示的含义,转化为实际问题中的数据.
详解
解:通过图象可以看出甲乙两人从同一起点同时出发,路程都是100米,甲用时10秒,乙用时12秒,
所以甲比乙先到达终点,所以A结论正确,不符合题意;
甲的速度为,乙的速度为,所以B选项错误符合题意;
C和D选项结论均正确,不符合题意.
故选B.
4.【答案】D
【解析】分析
本题考查了用图象反映变量间的关系,解题的关键是了解两个变量之间的关系以及对生活中的现象的了解.
冉冉升起的旗子随着时间的推移高度慢慢增加,对照选项中的图象可作出正确的判断.
详解
解:旗子是匀速上升的,且开始时是拿在同学手中,
旗子随着时间的增加,其高度也在不断增大,
只有D选项图象符合.
故选D.
5.【答案】C
【解析】分析
要找出准确反映时间与距离之间对应关系的图象,需分析在不同阶段中距离随时间变化的情况.
本题考查的是用图象反映变量间的关系,根据题意,对照各选项中的图象即可做出正确的选择.
详解
解:张大伯在行走的过程中,分三个阶段:
第一个:0到20min,距离从0变到了900m,
第二个:中间看报的时间内距离没有变化,为水平线,时间为20min到30min,
第三个:后15min,即30min到45min之间,距离从900米变到了0米,
由此可判断出C选项正确,A、D的图象没有第二个阶段,而B的第二个阶段时长应是20min到30min.
故选C.
6.【答案】C
【解析】
【分析】
此题主要考查变量x与y之间的关系式,关键是掌握已知的关系式,给出因变量的值时,解方程求出相应的自变量的值即可.
直接把代入,解方程即可.
【解答】
解:当时,,
解得:.
故选C.
7.【答案】A
【解析】分析
本题考查了用关系式表示变量间的关系、自变量取值范围及梯形面积先确定梯形ABCP的上底、下底和高,代入数据即可得梯形ABCP的面积y与DP长x之间的关系式.
详解
解:由梯形面积公式知,,,,
,
即,
且不与点C,D重合
,
.
故选A.
8.【答案】C
【解析】略
9.【答案】D
【解析】解:根据题意,从20分钟到40分钟哥哥在书店里看书,离家距离没有变化,是一条平行于x轴的线段.
故选:D.
根据哥哥看了20分钟书后,用15分钟返家即可判断哥哥的离家时间与距离之间的关系.
本题考查函数的图象,解题的关键是正确将文字语言转化为图形语言,本题属于基础题型.
10.【答案】A
【解析】解:不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,x表示漏水时间,y表示壶底到水面的高度,
随x的增大而减小,符合函数图象,
故选:A.
根据题意,可知y随x的增大而减小,符合函数图象,从而可以解答本题.
本题考查函数图象,解答本题的关键是明确题意,利用数形结合的思想解答.
11.【答案】D
【解析】分析
本题考查了用关系式表示的变量间关系,通过表格找出P增加1,则对应的C增加是关键根据表格中的数据可以得到P增加1,则对应的C增加,据此即可求解.
详解
解:根据表可以得到P增加1,则对应的C增加,
则C与P的对应关系是:.
故选D.
12.【答案】D
【解析】分析
从表格可知:时,,即没有加热时,油的温度为;每增加10秒,温度上升,则时,油温度;秒时,温度.
本题考查自变量与因变量的关系;能够通过表格确定自变量与因变量的变化关系是解题的关键.
详解
解:从表格可知:时,,即没有加热时,油的温度为,A正确;
每增加10秒,温度上升,则50秒时,油温度,B正确,D错误;
110秒时,温度,C正确;
故选D.
13.【答案】10
【解析】由题表可得,该汽车每行驶100千米的耗油量为升,
故答案为10.
14.【答案】18
【解析】解:,
把代入,得,
故答案为18.
15.【答案】
【解析】
【分析】
本题考查了函数关系式,利用三角形的面积是解题关键.根据三角形的面积公式,可得答案.
【解答】
解:,,
,
故答案为.
16.【答案】5升;升
【解析】
【分析】
此题这样考查了一次函数的应用问题,解题时首先正确理解题意,接着利用函数的性质即可解决问题.根据图象和已知条件可以求出每分钟进水,出水各多少升.
【解答】
解:由图可知:4分钟时,进水20升,每分钟进水量为升,
根据图象知道:每分钟出水升;
故答案为5升;升.
17.【答案】
【解析】解:由线段的和差,得,
由三角形的面积,得
,
化简,得,
故答案为:.
根据线段的和差,可得CE的长,根据三角形的面积,可得答案.
本题考查了函数关系式,利用三角形的面积公式是解题关键.
18.【答案】
【解析】解:由表格数据找出规律或由图形找出答案.
19.【答案】解:由长方形的周长公式,得.
由长方形的面积公式,得.
当时,,.
当x增加2时,y增加4,S增加32.
【解析】略
20.【答案】兔子、乌龟、1500
解:兔子在起初每分钟跑米,乌龟每分钟爬米
解:,
乌龟用了14分钟追上了正在睡觉的兔子
解:千米时米分钟,
,
兔子中间停下睡觉用了分钟
【解析】
【分析】
本题考查的是函数图象有关知识.
根据点D实际意义知全程的距离;
根据点A实际意义知兔子起初速度,由点D实际意义可知乌龟的速度;
利用兔子睡觉前行驶的路程是700米,结合乌龟的速度求出所用的时间;
根据比乌龟晚到了分钟求出兔子走完全程的时间,再得出兔子醒来后奔跑所用时间,求解可得.
【解答】
解:乌龟是一直跑的而兔子中间有休息的时刻;
折线OABC表示赛跑过程中兔子的路程与时间的关系;
线段OD表示赛跑过程中乌龟的路程与时间的关系;
由图象可知:赛跑的路程为1500米;
故答案为兔子、乌龟、1500;
见答案;
见答案;
见答案.
21.【答案】时间?
距离
【解析】解:在此变化过程中,自变量是时间,因变量是距离.
故答案为:时间;距离;
分钟.
所以小王在新华书店停留了10分钟;
小王从新华书店到商场的路程为米,所用时间为分钟,
小王从新华书店到商场的骑车速度是:米分.
根据图象作答即可;
由函数图象可知,分钟的路程没变,所以小王在新华书店停留了10分钟;
小王从新华书店到商场的路程为米,所用时间为分钟,根据速度路程时间,即可解答.
本题主要考查了函数图象的读图能力,要理解横纵坐标表示的含义以及小王的运动过程是解题的关键.
22.【答案】解:反映了易拉罐的底面半径和用铝量的关系,
其中,易拉罐的底面半径为自变量,用铝量为因变量.
当底面半径为时,易拉罐需要的用铝量为.
易拉罐的底面半径为时比较合适,因为此时用铝量较少,成本低.
【解析】略
23.【答案】解:.
由题意,知,解得,即该软件公司必须出售软件100套及以上才能不亏本.
【解析】略
第4页,共8页
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
