20.1第一课时 平行四边形的判定(1)
文档属性
| 名称 | 20.1第一课时 平行四边形的判定(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 417.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-19 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第20章 平行四边形的判定
§20.1 平行四边形的判定
1、平行四边形的定义?
定义:两组对边分别平行的四边形叫做平行四边形。
2、平行四边形有哪些重要的性质?
平行四边形的对边相等、对边平行.
平行四边形的对角相等
平行四边形的对角线互相平分
回顾与思考
我们已经知道,如果一个四边形是平行四边形,那么它就是一个中心对称图形,具有如下的一些性质:
1. 两组对边分别平行且相等;
2. 两组对角分别相等;
3. 两条对角线互相平分.
那么,怎样判定一个四边形是否是平行四边形呢?当然,我们可以根据平行四边形的原始定义: 两组对边分别平行的四边形是平行四边形加以判定.那么是否存在其他的判定方法?
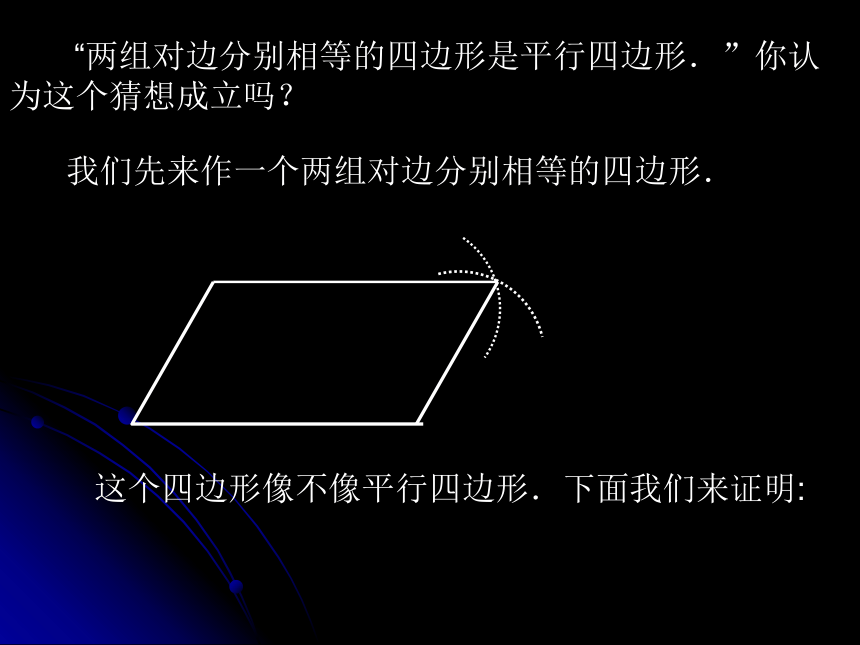
由平行四边形的性质“平行四边形的两组对边分别相等”逆向思考,互换题设与结论,可以得到:“两组对边分别相等的四边形是平行四边形.”你认为这个猜想成立吗?
“两组对边分别相等的四边形是平行四边形.”你认为这个猜想成立吗?
我们先来作一个两组对边分别相等的四边形.
这个四边形像不像平行四边形.下面我们来证明:
已知:四边形ABCD中, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
∵ AB=CD,AD=BC (已知)
B
D
A
C
3
4
1
2
证明:连结AC,
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4
(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
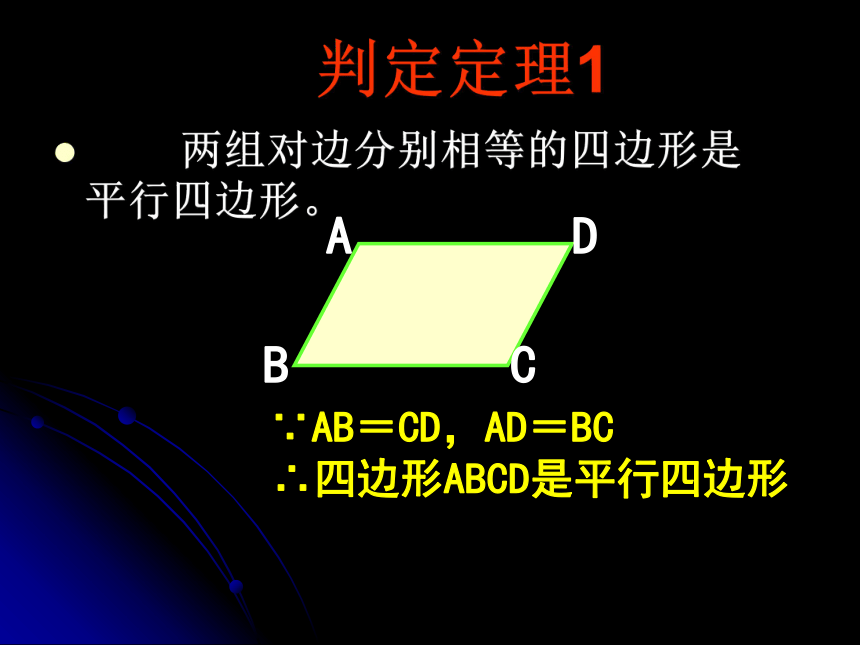
判定定理1
两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
A
B
C
D
平行四边形的性质:
平行四边形的两组对边分别相等
比一比
平行四边形的判定:
两组对边分别相等的四边形是平行四边形。
平行四边形的性质:
平行四边形的两组对边分别平行
再比一比
平行四边形的判定:
两组对边分别平行的四边形是平行四边形。
由平行四边形的性质,得到的另一个猜想是:
“一组对边平行且相等的四边形是平行四边形.”
如图,试作一个有一组对边平行且相等的四边形.
∵ AD∥BC
B
D
A
C
已知:四边形ABCD中, AD=BC,AD∥BC
求证:四边形ABCD是平行四边形
3
4
证明:连结AC
∴∠3=∠4
又∵ AD=CB AC=CA
∴△ABC≌△CDA(SAS)
∴AB=CD
(全等三角形的对应边相等)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
∵ AD=BC
判定定理2
一组对边平行且相等的四边形是平行四边形。
∵AB=CD,AD∥BC
∴四边形ABCD是平行四边形
A
B
C
D
“平行且相等”常用符号“? ”来表示.如图, AB=CD且AB∥CD,可以记作“AB? CD”,读作“AB平行且等于CD”.
例1.如图,在?ABCD中,E、F分别是对边BC和AD上的两点,且AF=CE,求证: 四边形AECF为平行四边形.
分析 我们已经有了三种判定平行四边形的方法,根据已知条件有AF=CE,若运用现在得到的判定方法,只须证明AF∥CE.
证明 ∵ 四边形ABCD是平行四边形,
∴ AD∥BC(平行四边形的对边平行)
即AF∥CE.
又∵ AF=CE,
∴ 四边形AECF为平行四边形
(一组对边平行且相等的四边形是平行四边形).
练习
1. 在下面的格点图中,以格点为顶点,你能画出多少个平行四边形?
解:3个
2. 如图,在平行四边形ABCD中,已知M和N分别是AB和DC上的中点,试证明四边形BNDM也是平行四边形.
平行四边形的判定方法:
理一理
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
知识就是力量!
知识就是源泉!
1.延长⊿ABC的中线AD至E,使DE=AD,求证:四边形ABEC是平行四边形
2.AC是□ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足为M、N,求证:四边形BMDN是平行四边形
A
B
C
D
M
N
第20章 平行四边形的判定
§20.1 平行四边形的判定
1、平行四边形的定义?
定义:两组对边分别平行的四边形叫做平行四边形。
2、平行四边形有哪些重要的性质?
平行四边形的对边相等、对边平行.
平行四边形的对角相等
平行四边形的对角线互相平分
回顾与思考
我们已经知道,如果一个四边形是平行四边形,那么它就是一个中心对称图形,具有如下的一些性质:
1. 两组对边分别平行且相等;
2. 两组对角分别相等;
3. 两条对角线互相平分.
那么,怎样判定一个四边形是否是平行四边形呢?当然,我们可以根据平行四边形的原始定义: 两组对边分别平行的四边形是平行四边形加以判定.那么是否存在其他的判定方法?
由平行四边形的性质“平行四边形的两组对边分别相等”逆向思考,互换题设与结论,可以得到:“两组对边分别相等的四边形是平行四边形.”你认为这个猜想成立吗?
“两组对边分别相等的四边形是平行四边形.”你认为这个猜想成立吗?
我们先来作一个两组对边分别相等的四边形.
这个四边形像不像平行四边形.下面我们来证明:
已知:四边形ABCD中, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
∵ AB=CD,AD=BC (已知)
B
D
A
C
3
4
1
2
证明:连结AC,
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4
(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
判定定理1
两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
A
B
C
D
平行四边形的性质:
平行四边形的两组对边分别相等
比一比
平行四边形的判定:
两组对边分别相等的四边形是平行四边形。
平行四边形的性质:
平行四边形的两组对边分别平行
再比一比
平行四边形的判定:
两组对边分别平行的四边形是平行四边形。
由平行四边形的性质,得到的另一个猜想是:
“一组对边平行且相等的四边形是平行四边形.”
如图,试作一个有一组对边平行且相等的四边形.
∵ AD∥BC
B
D
A
C
已知:四边形ABCD中, AD=BC,AD∥BC
求证:四边形ABCD是平行四边形
3
4
证明:连结AC
∴∠3=∠4
又∵ AD=CB AC=CA
∴△ABC≌△CDA(SAS)
∴AB=CD
(全等三角形的对应边相等)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
∵ AD=BC
判定定理2
一组对边平行且相等的四边形是平行四边形。
∵AB=CD,AD∥BC
∴四边形ABCD是平行四边形
A
B
C
D
“平行且相等”常用符号“? ”来表示.如图, AB=CD且AB∥CD,可以记作“AB? CD”,读作“AB平行且等于CD”.
例1.如图,在?ABCD中,E、F分别是对边BC和AD上的两点,且AF=CE,求证: 四边形AECF为平行四边形.
分析 我们已经有了三种判定平行四边形的方法,根据已知条件有AF=CE,若运用现在得到的判定方法,只须证明AF∥CE.
证明 ∵ 四边形ABCD是平行四边形,
∴ AD∥BC(平行四边形的对边平行)
即AF∥CE.
又∵ AF=CE,
∴ 四边形AECF为平行四边形
(一组对边平行且相等的四边形是平行四边形).
练习
1. 在下面的格点图中,以格点为顶点,你能画出多少个平行四边形?
解:3个
2. 如图,在平行四边形ABCD中,已知M和N分别是AB和DC上的中点,试证明四边形BNDM也是平行四边形.
平行四边形的判定方法:
理一理
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
知识就是力量!
知识就是源泉!
1.延长⊿ABC的中线AD至E,使DE=AD,求证:四边形ABEC是平行四边形
2.AC是□ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足为M、N,求证:四边形BMDN是平行四边形
A
B
C
D
M
N
