2020-2021学年人教版八年级下册数学第18章《平行四边形》单元试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》单元试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 446.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 14:42:03 | ||
图片预览



文档简介
第18章
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
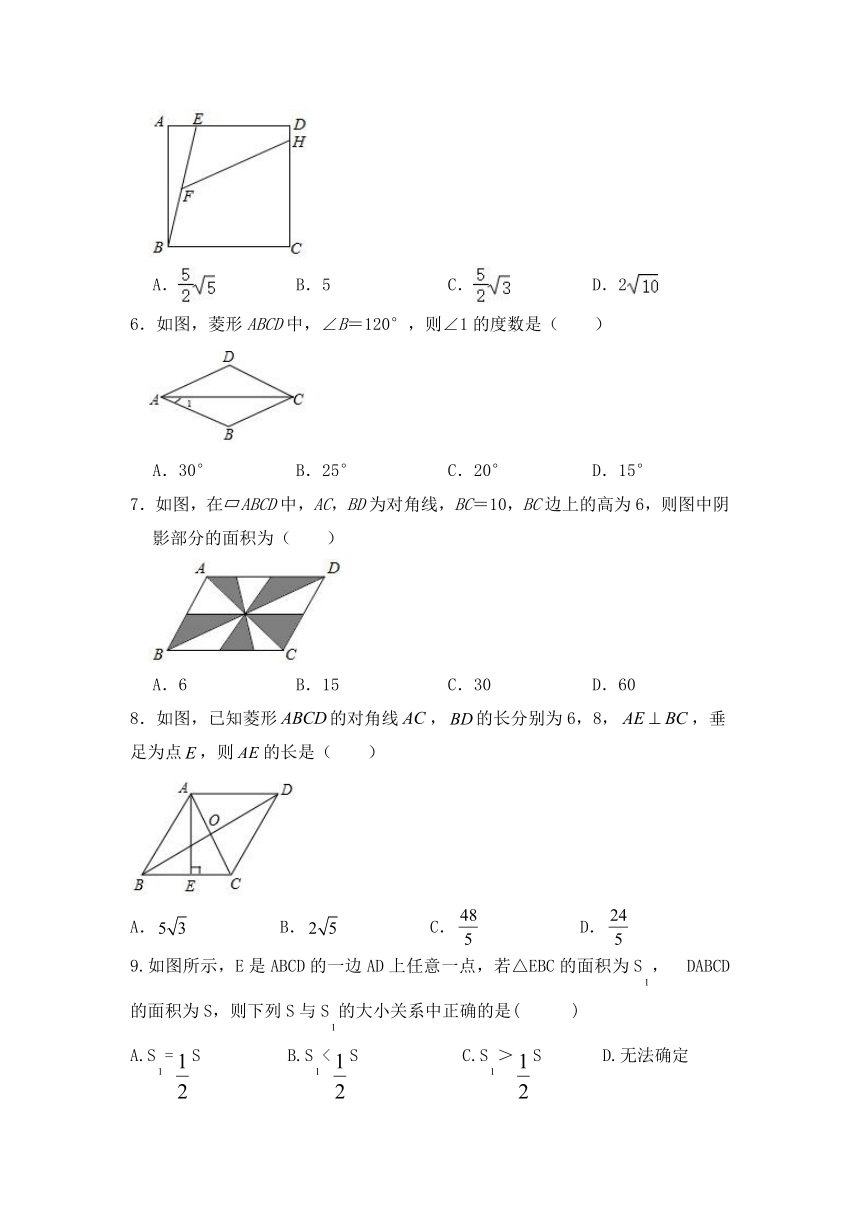
1.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=(
)
A.5
B.4
C.3.5
D.3
2.菱形的两条对角线分别是12和16,则此菱形的边长是(
)
A.10
B.8
C.6
D.5
3.
在?ABCD中,添加下列条件能够判定?ABCD是菱形的是( )
A.AC=BD
B.AB=CD
C.AB⊥BC
D.AC⊥BD
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,已知菱形的对角线,的长分别为6,8,,垂足为点,则的长是(
)
A.
B.
C.
D.
9.如图所示,E是ABCD的一边AD上任意一点,若△EBC的面积为S,?DABCD的面积为S,则下列S与S的大小关系中正确的是(
)
A.S=S
B.SC.S>S
D.无法确定
10.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是(
)
A.4.8
B.5
C.6
D.7.2
二.填空题(每题4分,共20分)
11.
如图,在菱形中,在上,点在上,则的最小值为
12.
某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
13.
如图,四边形为正方形,以为边向正方形外作正方形,与相交于点,则
14.
如图,正方形中,是对角线的交点,过点作,分别交于,若,则
15.
如图,在正方形中,点为正方形内的两点,且,则
三.解答题(每题10分,共50分)
16.
如图,、分别是平行四边形的、边上的点,且.
⑴求证:≌;
⑵若、分别是、的中点,连接、,试判断四边形是怎样的四边形,并证明你的结论.
17.
如图,将?ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
18.
如图,是矩形的对角线交点,过点作分别交、于、,若,,求四边形的面积.
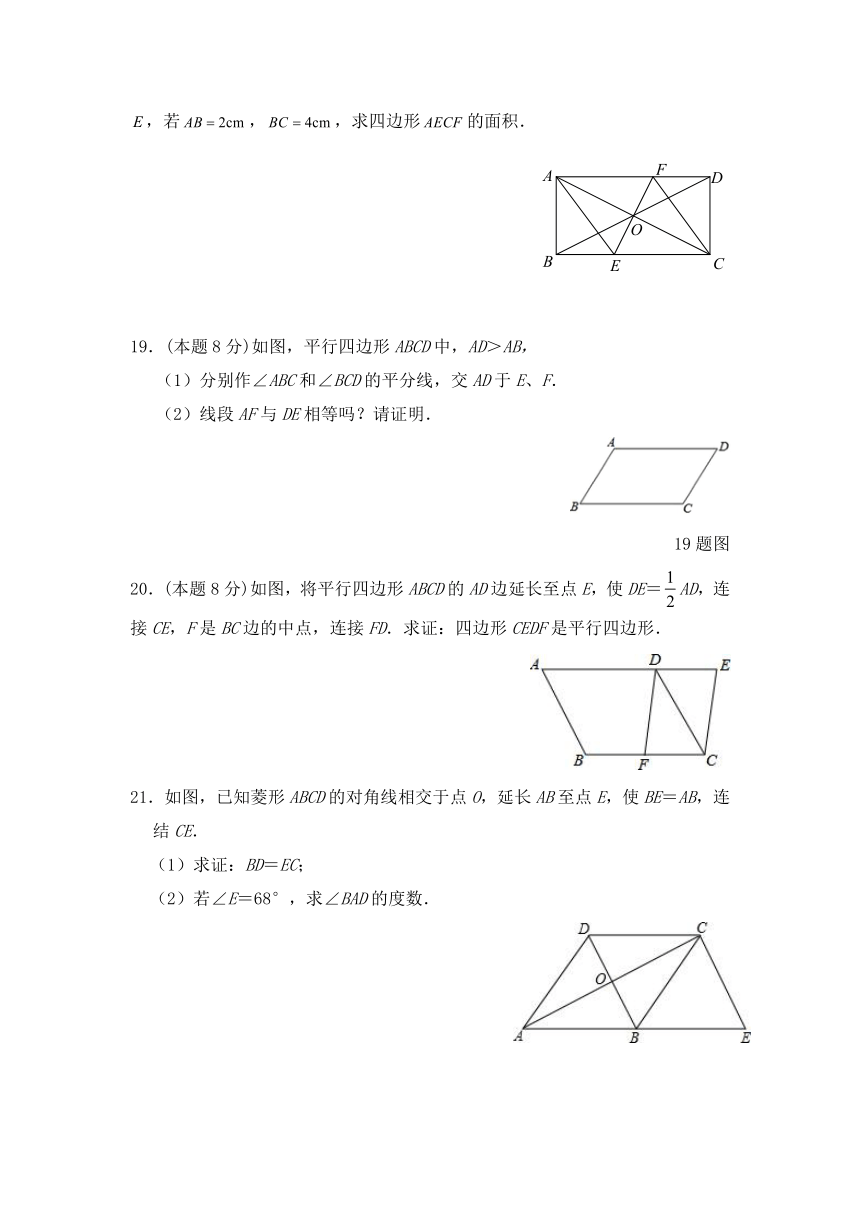
19.(本题8分)如图,平行四边形ABCD中,AD>AB,
(1)分别作∠ABC和∠BCD的平分线,交AD于E、F.
(2)线段AF与DE相等吗?请证明.
19题图
20.(本题8分)如图,将平行四边形ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.
21.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=68°,求∠BAD的度数.
22.如图,在矩形ABCD中,E是边CD的中点,点M是边AD上一点(与点A,D不重合),射线ME与BC的延长线交于点N.
(1)求证:△MDE≌△NCE;
(2)过点E作EF∥CB交BM于点F,当MB=MN时,求证:AM=EF.
23.已知,矩形ABCD的对角线AC、BD相交于点O.
(Ⅰ)如图①,若AB=6,BC=8,则BD=
,OD=
;
(Ⅱ)如图②,DE∥AC,CE∥BD,求证:四边形OCED是菱形.
参考答案
一.选择题
1.B
2.A
3.
D.
4.
C.
5.
D.
6.
C.
7.
C.
8.
D.
9.
A.10.A
二.填空题(共5小题)
11.
【答案】
【解析】关于对称,连交于,且
为最小值
12.
【答案】
【解析】由图形可知:可推出
13.
【答案】
14.5
15.45°
三.解答题(共5小题)
16.
【答案】
⑴由是平行四边形可知,,
又,故≌
⑵由(1)可知,,
又,,∴
而∥,∴有
∴,∴∥
∴四边形为平行四边形
17.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥FC.(2分)
∵F是BC的中点,
∴FC=BC=AD,
∵DE=AD,∴FC=DE,(4分)
∴四边形CEDF是平行四边形.(5分)
(2)
解图
解:如解图,过点D作DH⊥BC于点H.
由(1)知四边形DECF是平行四边形,
∴DF=CE.(6分)
∵四边形ABCD是平行四边形,∠A=60°,AB=3,AD=4,
∴BC=4,CD=3,∠BCD=60°,(8分)
在Rt△DHC中,HC=DC·cos∠HCD=,
DH=DC·sin∠HCD=,
∵F是BC的中点,
∴FC=2,
∴FH=FC-HC=2-=,(10分)
在Rt△DFH中,由勾股定理得DF==
=,
∴CE=.(12分)
18.
【答案】
【解析】由为矩形可知,
又∵∥,∴
又,∴≌.
故
从而可知为菱形,∴.
又∵,
∴在直角中,由勾股定理有,
解得.故四边形的面积为()
∵
,
,∴
18.3:4
解:证明:∵四边形ABCD是平行四边形,
∴AB=CD,
AD=BC,
又∵AE⊥BC,AF⊥DC,
∴平行四边形ABCD的面积=BC×AE=CD×AF,即AD×AE=AB×AF,
又AB:AD=3:4,
∴.
19.
解:(1)如图:BE、CF即∠ABC和∠BCD的平分线,
(2)AF与DE相等.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∴∠AEB=∠EBC,
∵BE平分∠ABC,∴∠ABE=∠CBE,
∴∠ABE=∠AEB,∴AB=AE,
同理可得:DF=CD,
∴AE=DF,即AF+EF=DE+EF,∴AF=DE.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=AD,F是BC边的中点,
∴FC=BC=AD=DE,又∵DE∥FC,
∴四边形CEDF是平行四边形.
21.解:(1)证明:∵四边形ABCD是菱形,
∴DC∥AB,DC=AB.
∵BE=AB,
∴DC∥BE,DC=BE.
∴四边形BDCE为平行四边形.
∴BD=EC.
(2)∵四边形BDCE为平行四边形,
∴BD∥CE.
∴∠DBA=∠E=68°.
∵菱形ABCD,
∴AC⊥BD,AC平分∠BAD,
∴∠BAO=90°﹣∠DBA=22°.
∴∠BAD=2∠BAO=44°.
22.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DME=∠CNE,∠MDE=∠ECN,
∵E为CD的中点,
∴DE=CE,
∴△MDE≌△NCE(AAS);
(2)证明:过点M作MG⊥BN于点G,
∵BM=MN,
∴BG=BN=BN,
∵矩形ABCD中,∠A=∠ABG=90°,
又∵MG⊥BN,
∴∠BGM=90°,
∴四边形ABGM为矩形,
∴AM=BG=,
∵EF∥BN,E为DC的中点,
∴F为BM的中点,
∴EF=BN,
∴AM=EF.
23.(1)解:∵矩形ABCD对角线AC、BD相交于点O,
∵AB=6,BC=8,
由勾股定理得:AC=BD=10,
∴OD=BD=5;
故答案为:10,5;
(2)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴AB=CD,OA=OC,OB=OD,
∴OC=OD,
∴四边形OCED是菱形;
《平行四边形》单元测试
.
题号
一
二
三
总分
16
17
18
19
20
分数
一.选择题(每题3分,共30分)
1.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=(
)
A.5
B.4
C.3.5
D.3
2.菱形的两条对角线分别是12和16,则此菱形的边长是(
)
A.10
B.8
C.6
D.5
3.
在?ABCD中,添加下列条件能够判定?ABCD是菱形的是( )
A.AC=BD
B.AB=CD
C.AB⊥BC
D.AC⊥BD
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,已知菱形的对角线,的长分别为6,8,,垂足为点,则的长是(
)
A.
B.
C.
D.
9.如图所示,E是ABCD的一边AD上任意一点,若△EBC的面积为S,?DABCD的面积为S,则下列S与S的大小关系中正确的是(
)
A.S=S
B.S
D.无法确定
10.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是(
)
A.4.8
B.5
C.6
D.7.2
二.填空题(每题4分,共20分)
11.
如图,在菱形中,在上,点在上,则的最小值为
12.
某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
13.
如图,四边形为正方形,以为边向正方形外作正方形,与相交于点,则
14.
如图,正方形中,是对角线的交点,过点作,分别交于,若,则
15.
如图,在正方形中,点为正方形内的两点,且,则
三.解答题(每题10分,共50分)
16.
如图,、分别是平行四边形的、边上的点,且.
⑴求证:≌;
⑵若、分别是、的中点,连接、,试判断四边形是怎样的四边形,并证明你的结论.
17.
如图,将?ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
18.
如图,是矩形的对角线交点,过点作分别交、于、,若,,求四边形的面积.
19.(本题8分)如图,平行四边形ABCD中,AD>AB,
(1)分别作∠ABC和∠BCD的平分线,交AD于E、F.
(2)线段AF与DE相等吗?请证明.
19题图
20.(本题8分)如图,将平行四边形ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.
21.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=68°,求∠BAD的度数.
22.如图,在矩形ABCD中,E是边CD的中点,点M是边AD上一点(与点A,D不重合),射线ME与BC的延长线交于点N.
(1)求证:△MDE≌△NCE;
(2)过点E作EF∥CB交BM于点F,当MB=MN时,求证:AM=EF.
23.已知,矩形ABCD的对角线AC、BD相交于点O.
(Ⅰ)如图①,若AB=6,BC=8,则BD=
,OD=
;
(Ⅱ)如图②,DE∥AC,CE∥BD,求证:四边形OCED是菱形.
参考答案
一.选择题
1.B
2.A
3.
D.
4.
C.
5.
D.
6.
C.
7.
C.
8.
D.
9.
A.10.A
二.填空题(共5小题)
11.
【答案】
【解析】关于对称,连交于,且
为最小值
12.
【答案】
【解析】由图形可知:可推出
13.
【答案】
14.5
15.45°
三.解答题(共5小题)
16.
【答案】
⑴由是平行四边形可知,,
又,故≌
⑵由(1)可知,,
又,,∴
而∥,∴有
∴,∴∥
∴四边形为平行四边形
17.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥FC.(2分)
∵F是BC的中点,
∴FC=BC=AD,
∵DE=AD,∴FC=DE,(4分)
∴四边形CEDF是平行四边形.(5分)
(2)
解图
解:如解图,过点D作DH⊥BC于点H.
由(1)知四边形DECF是平行四边形,
∴DF=CE.(6分)
∵四边形ABCD是平行四边形,∠A=60°,AB=3,AD=4,
∴BC=4,CD=3,∠BCD=60°,(8分)
在Rt△DHC中,HC=DC·cos∠HCD=,
DH=DC·sin∠HCD=,
∵F是BC的中点,
∴FC=2,
∴FH=FC-HC=2-=,(10分)
在Rt△DFH中,由勾股定理得DF==
=,
∴CE=.(12分)
18.
【答案】
【解析】由为矩形可知,
又∵∥,∴
又,∴≌.
故
从而可知为菱形,∴.
又∵,
∴在直角中,由勾股定理有,
解得.故四边形的面积为()
∵
,
,∴
18.3:4
解:证明:∵四边形ABCD是平行四边形,
∴AB=CD,
AD=BC,
又∵AE⊥BC,AF⊥DC,
∴平行四边形ABCD的面积=BC×AE=CD×AF,即AD×AE=AB×AF,
又AB:AD=3:4,
∴.
19.
解:(1)如图:BE、CF即∠ABC和∠BCD的平分线,
(2)AF与DE相等.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∴∠AEB=∠EBC,
∵BE平分∠ABC,∴∠ABE=∠CBE,
∴∠ABE=∠AEB,∴AB=AE,
同理可得:DF=CD,
∴AE=DF,即AF+EF=DE+EF,∴AF=DE.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=AD,F是BC边的中点,
∴FC=BC=AD=DE,又∵DE∥FC,
∴四边形CEDF是平行四边形.
21.解:(1)证明:∵四边形ABCD是菱形,
∴DC∥AB,DC=AB.
∵BE=AB,
∴DC∥BE,DC=BE.
∴四边形BDCE为平行四边形.
∴BD=EC.
(2)∵四边形BDCE为平行四边形,
∴BD∥CE.
∴∠DBA=∠E=68°.
∵菱形ABCD,
∴AC⊥BD,AC平分∠BAD,
∴∠BAO=90°﹣∠DBA=22°.
∴∠BAD=2∠BAO=44°.
22.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DME=∠CNE,∠MDE=∠ECN,
∵E为CD的中点,
∴DE=CE,
∴△MDE≌△NCE(AAS);
(2)证明:过点M作MG⊥BN于点G,
∵BM=MN,
∴BG=BN=BN,
∵矩形ABCD中,∠A=∠ABG=90°,
又∵MG⊥BN,
∴∠BGM=90°,
∴四边形ABGM为矩形,
∴AM=BG=,
∵EF∥BN,E为DC的中点,
∴F为BM的中点,
∴EF=BN,
∴AM=EF.
23.(1)解:∵矩形ABCD对角线AC、BD相交于点O,
∵AB=6,BC=8,
由勾股定理得:AC=BD=10,
∴OD=BD=5;
故答案为:10,5;
(2)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴AB=CD,OA=OC,OB=OD,
∴OC=OD,
∴四边形OCED是菱形;
