2020-2021学年人教版八年级下册数学第18章《平行四边形》单元试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》单元试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 276.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 14:44:25 | ||
图片预览

文档简介
第18章
《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.如图,在?ABCD中,已知AC=4
cm,若△ACD的周长为13
cm,则?ABCD的周长为( )
(第1题)
A.26
cm
B.24
cm
C.20
cm
D.18
cm
2.如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3
cm,则AB的长为( )
A.12
cm
B.9
cm
C.6
cm
D.3
cm
(第2题)
3.下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=DC,AD=BC
B.AB∥DC,AD∥BC
C.AB∥DC,AD=BC
D.AB∥DC,AB=DC
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
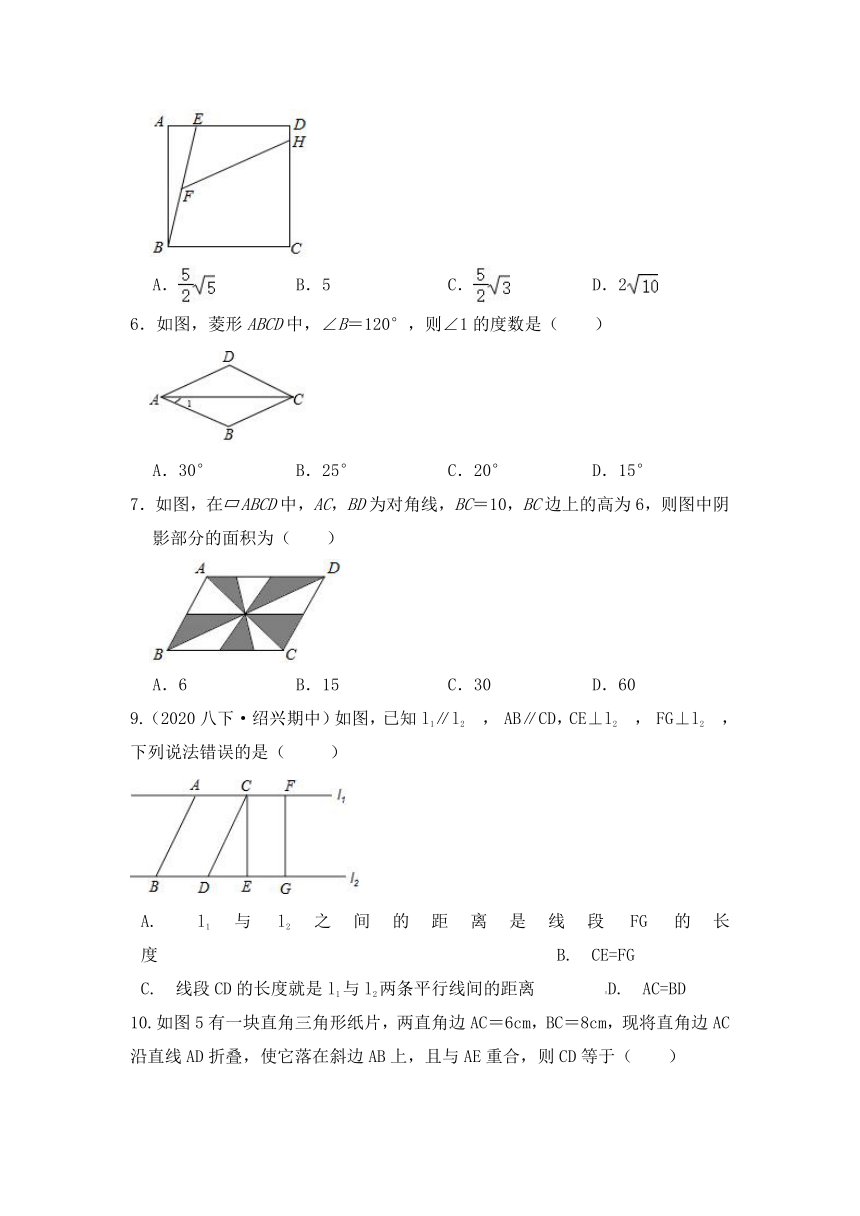
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
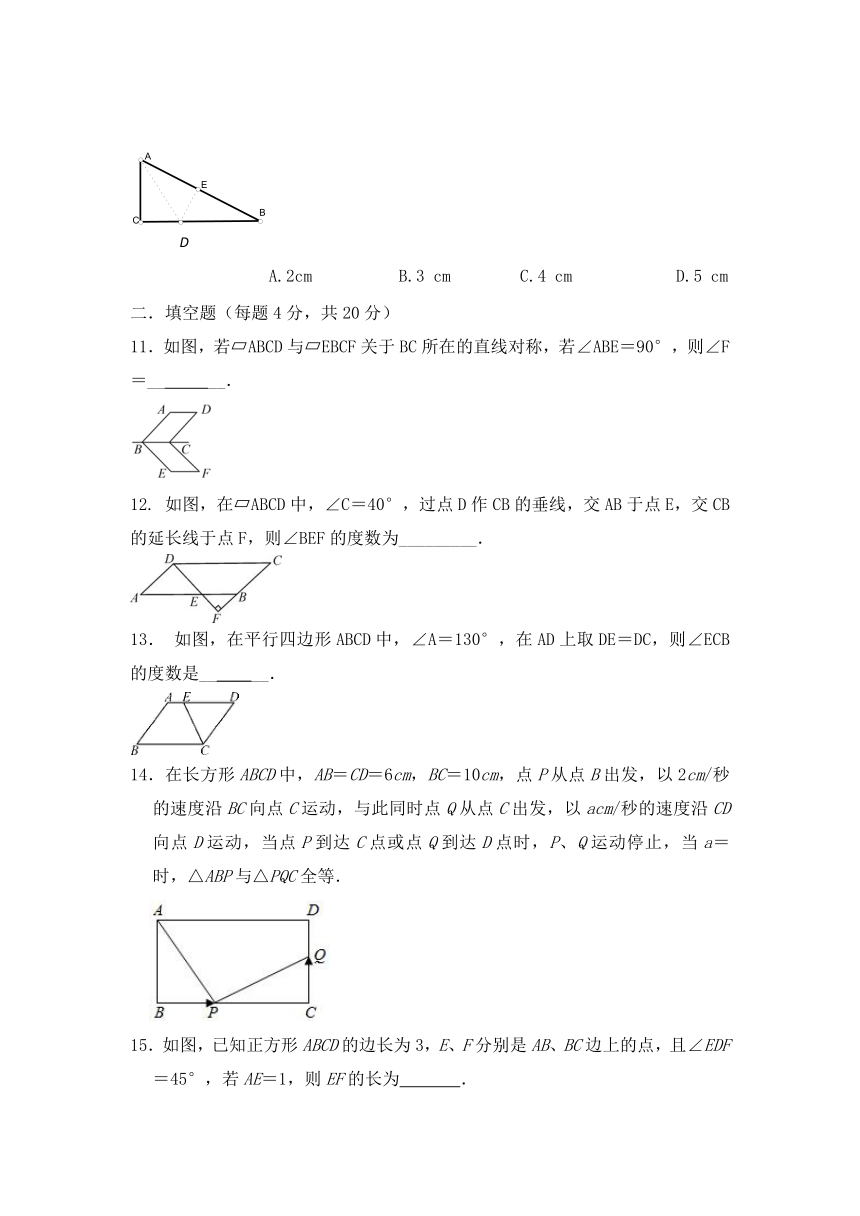
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
9.(2020八下·绍兴期中)如图,已知l1∥l2
,
AB∥CD,CE⊥l2
,
FG⊥l2
,
下列说法错误的是(??
)
A.?l1与l2之间的距离是线段FG的长度???????????????????????B.?CE=FG
C.?线段CD的长度就是l1与l2两条平行线间的距离????D.?AC=BD
10.如图5有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于(
)
A.2cm
B.3
cm
C.4
cm
D.5
cm
二.填空题(每题4分,共20分)
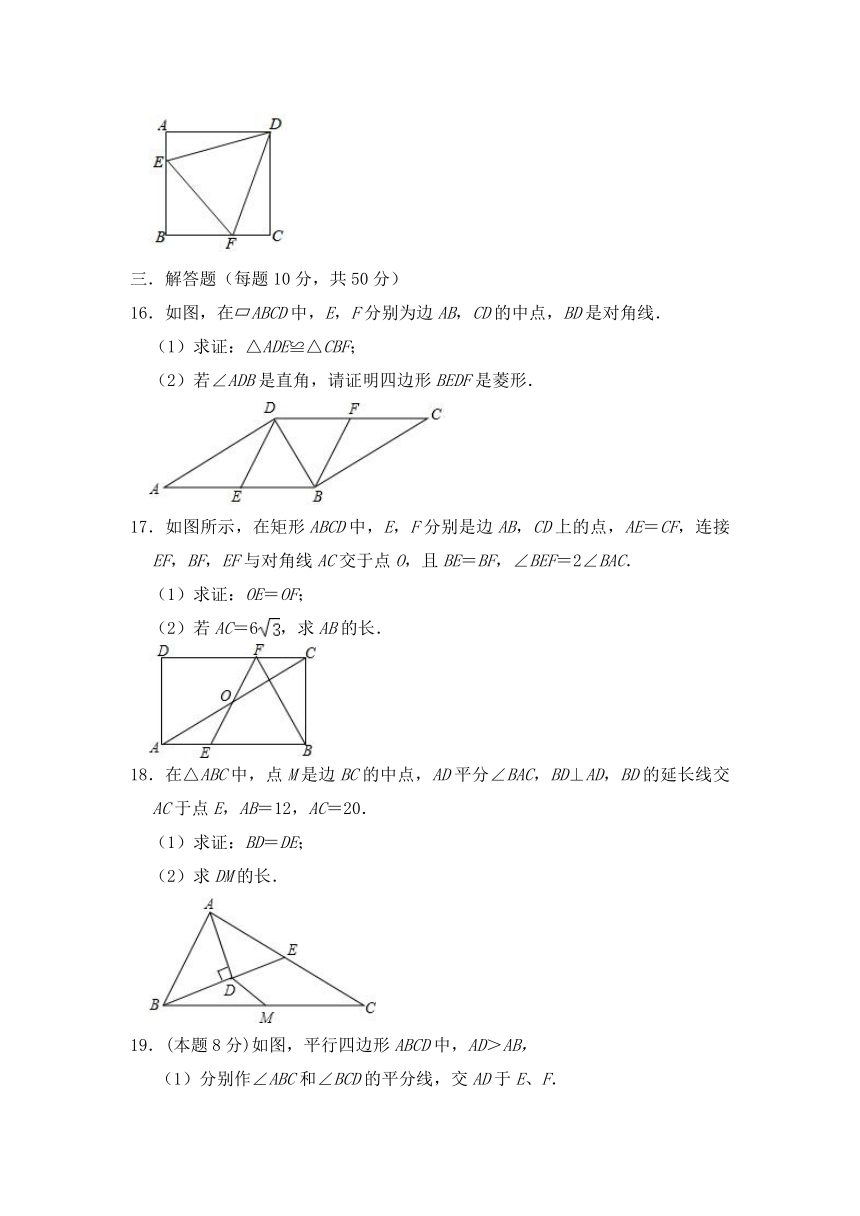
11.如图,若?ABCD与?EBCF关于BC所在的直线对称,若∠ABE=90°,则∠F=__
__.
12.
如图,在?ABCD中,∠C=40°,过点D作CB的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为_________.
13.
如图,在平行四边形ABCD中,∠A=130°,在AD上取DE=DC,则∠ECB的度数是________.
14.在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,与此同时点Q从点C出发,以acm/秒的速度沿CD向点D运动,当点P到达C点或点Q到达D点时,P、Q运动停止,当a=
时,△ABP与△PQC全等.
15.如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,若AE=1,则EF的长为
.
三.解答题(每题10分,共50分)
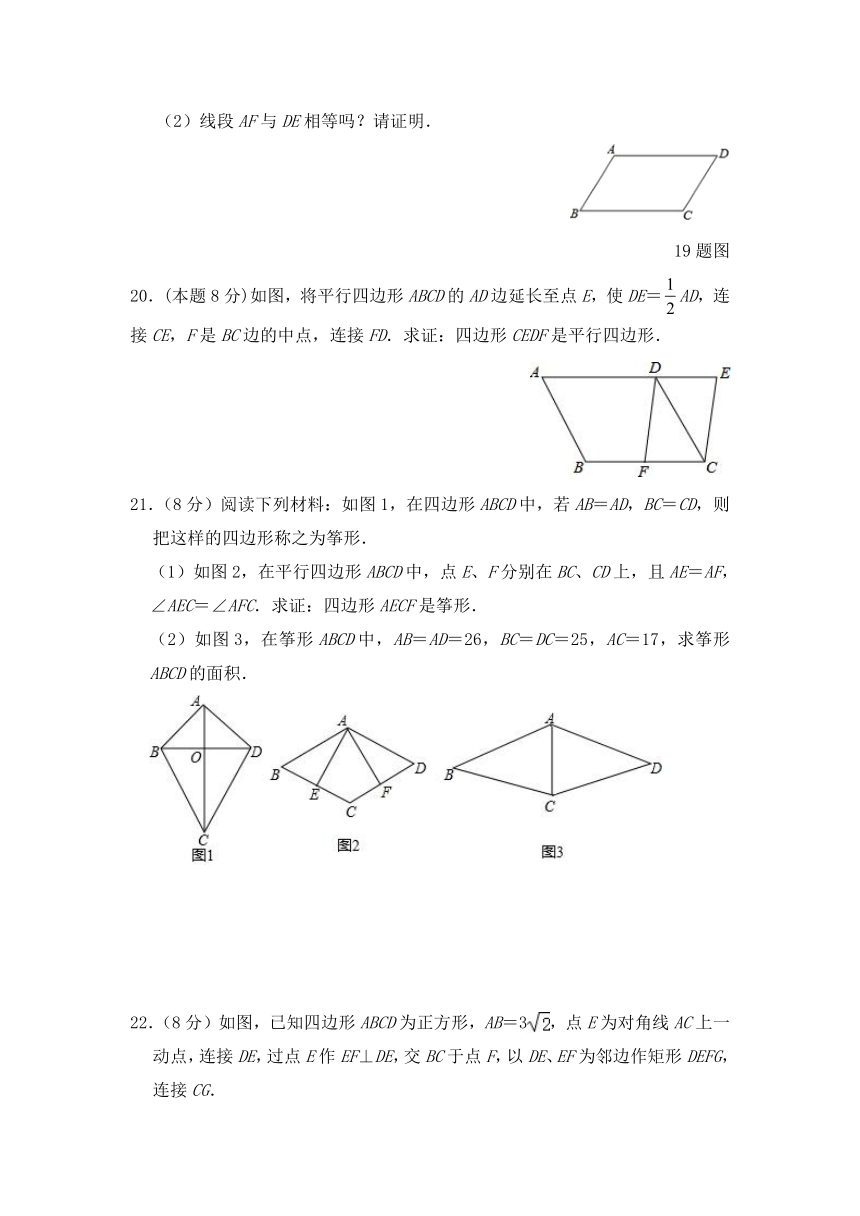
16.如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
17.如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若AC=6,求AB的长.
18.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
19.(本题8分)如图,平行四边形ABCD中,AD>AB,
(1)分别作∠ABC和∠BCD的平分线,交AD于E、F.
(2)线段AF与DE相等吗?请证明.
19题图
20.(本题8分)如图,将平行四边形ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.
21.(8分)阅读下列材料:如图1,在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.
(1)如图2,在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.
(2)如图3,在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.
22.(8分)如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
23.(10分)如图1,点O是菱形ABCD对角线的交点,已知菱形的边长为12,∠ABC=60°.
(1)求BD的长;
(2)如图2,点E是菱形边上的动点,连接EO并延长交对边于点G,将射线OE绕点O顺时针旋转30°交菱形于点H,延长HO交对边于点F.
①求证:四边形EFGH是平行四边形;
②若动点E从点B出发,以每秒1个单位长度沿B→A→D的方向在BA和AD上运动,设点E运动的时间为t,当t为何值时,四边形EFGH为矩形.
参考答案
一.选择题
1.D
2.C
3.
C
4.
C.
5.
D.
6.
C.
7.
C.
8.
D.
9.
C.10.A
二.填空题(共5小题)
11.
45°
12.
50°
13.
65°
14.
2或2.4.
15.
.
三.解答题(共5小题)
16.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS).
(2)证明:∵E、F分别为边AB、CD的中点,
∴DF=DC,BE=AB,
又∵在?ABCD中,AB∥CD,AB=CD,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∵DB⊥BC,
∴∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边DC的中点,
∴BF=DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形.
17.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAE=∠ACF,∠CFO=∠AEO,
在△AOE和△COF中,,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:连接OB,如图所示:
∵BF=BE,OE=OF,
∴BO⊥EF,
由(1)知,△AOE≌△COF,
∴OA=OC,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BO=AC=OA,
∴∠BAC=∠OBA,
又∠BEF=2∠BAC,
∴∠BEF=2∠OBE,
而Rt△OBE中,∠BEO+∠OBE=90°,
∴∠BAC=30°,
∴BC=AC=3,
∴AB==9.
18.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
19.
解:(1)如图:BE、CF即∠ABC和∠BCD的平分线,
(2)AF与DE相等.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∴∠AEB=∠EBC,
∵BE平分∠ABC,∴∠ABE=∠CBE,
∴∠ABE=∠AEB,∴AB=AE,
同理可得:DF=CD,
∴AE=DF,即AF+EF=DE+EF,∴AF=DE.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=AD,F是BC边的中点,
∴FC=BC=AD=DE,又∵DE∥FC,
∴四边形CEDF是平行四边形.
21.解:(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵∠AEC=∠AFC,∠AEC+∠AEB=∠AFC+∠AFD=180°,
∴∠AEB=∠AFD,
∵AE=AF,
∴△AEB≌△AFD(AAS),
∴AB=AD,BE=DF,
∴平行四边形ABCD是菱形,
∴BC=DC,
∴EC=FC,
∴四边形AECF是筝形.
(2)如图∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS),
∴S△ABC=S△ADC,
过点B作BH⊥AC,垂足为H,
在Rt△ABH中,BH2=AB2﹣AH2=262﹣AH2,
在Rt△CBH中,BH2=CB2﹣CH2=252﹣(17﹣AH)2,
∴262﹣AH2=252﹣(17﹣AH)2,
∴AH=10,
∴BH==24,
∴S△ABC=×17×24=204.∴筝形ABCD的面积=2S△ABC=408.
22.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
23.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,∥ABO=∠OBC=30°,
∴AO=AB=6,
∴OB=AB?cos30°=6,
∴BD=2BO=12.
(2)①∵四边形ABCD是菱形,
∴AB∥CD,BO=OD,
∴∠EBO=∠GDO
∵∠BOE=∠DOG,
∴△EOB≌△GOD,
∴EO=GO,同理可得HO=FO,
∴四边形EFGH是平行四边形.
②a、当点E、H都在AB上时,四边形EFGH是矩形,作∠EOH的平分线OM,
∵OE=OH,
∴OM⊥EH.
∴∠MOB=90°﹣∠ABO=60°,
∵∠MOE=∠EOH=15°,
∴∠EOB=∠MOB﹣∠MOE=45°,作EN⊥OB于N.设ON=EN=x,则NB=x,
∵OB=6,
∴x+x=6,
∴x=9﹣3,
∴BE=2EN=18﹣6,
∴t=18﹣6时,四边形EFGH是矩形.
b、当点E在AB上,点H在AD上,四边形EFGH是矩形.
由菱形和矩形都是轴对称图形可知,∠AOE=∠AOH=15°,
∴∠EOB=90°﹣15°=75°,
∵∠ABO=30°,
∴∠BEO=180°﹣∠EOB﹣∠ABO=75°,
∴∠BEO=∠BOE,
∴BE=BO=6,
∴t=6时,四边形EFGH是矩形.
c、当点E、H都在AD上时,四边形EFGH是矩形.
由b同理可证:DE=DO=6,
∴AB+AE=AB+AD﹣DE=24﹣6
∴t=24﹣6时,四边形EFGH是矩形.
d、当点E在AD上,点H在DC上,四边形EFGH是矩形.
由菱形、矩形都是轴对称图形可知,∠DOE=∠HOE=15°,
∴∠EOA=90°﹣15°=75°,
∵∠OAD=60°,过点O作OK⊥AD,
∴∠AOK=90°﹣∠OAD=30°,
∴∠KOE=75°﹣30°=45°,
∴KE=OK,
∴AE=AK+KE=3+3,
∴BA+AE=15+3,
∴t=15+3,
∴t=15+3时,四边形EFGH是矩形.
综上所述,t为18﹣6,6,24﹣6,15+3时,四边形EFGH是矩形.
D
《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.如图,在?ABCD中,已知AC=4
cm,若△ACD的周长为13
cm,则?ABCD的周长为( )
(第1题)
A.26
cm
B.24
cm
C.20
cm
D.18
cm
2.如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3
cm,则AB的长为( )
A.12
cm
B.9
cm
C.6
cm
D.3
cm
(第2题)
3.下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=DC,AD=BC
B.AB∥DC,AD∥BC
C.AB∥DC,AD=BC
D.AB∥DC,AB=DC
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
9.(2020八下·绍兴期中)如图,已知l1∥l2
,
AB∥CD,CE⊥l2
,
FG⊥l2
,
下列说法错误的是(??
)
A.?l1与l2之间的距离是线段FG的长度???????????????????????B.?CE=FG
C.?线段CD的长度就是l1与l2两条平行线间的距离????D.?AC=BD
10.如图5有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于(
)
A.2cm
B.3
cm
C.4
cm
D.5
cm
二.填空题(每题4分,共20分)
11.如图,若?ABCD与?EBCF关于BC所在的直线对称,若∠ABE=90°,则∠F=__
__.
12.
如图,在?ABCD中,∠C=40°,过点D作CB的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为_________.
13.
如图,在平行四边形ABCD中,∠A=130°,在AD上取DE=DC,则∠ECB的度数是________.
14.在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,与此同时点Q从点C出发,以acm/秒的速度沿CD向点D运动,当点P到达C点或点Q到达D点时,P、Q运动停止,当a=
时,△ABP与△PQC全等.
15.如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,若AE=1,则EF的长为
.
三.解答题(每题10分,共50分)
16.如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
17.如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若AC=6,求AB的长.
18.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
19.(本题8分)如图,平行四边形ABCD中,AD>AB,
(1)分别作∠ABC和∠BCD的平分线,交AD于E、F.
(2)线段AF与DE相等吗?请证明.
19题图
20.(本题8分)如图,将平行四边形ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.
21.(8分)阅读下列材料:如图1,在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.
(1)如图2,在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.
(2)如图3,在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.
22.(8分)如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
23.(10分)如图1,点O是菱形ABCD对角线的交点,已知菱形的边长为12,∠ABC=60°.
(1)求BD的长;
(2)如图2,点E是菱形边上的动点,连接EO并延长交对边于点G,将射线OE绕点O顺时针旋转30°交菱形于点H,延长HO交对边于点F.
①求证:四边形EFGH是平行四边形;
②若动点E从点B出发,以每秒1个单位长度沿B→A→D的方向在BA和AD上运动,设点E运动的时间为t,当t为何值时,四边形EFGH为矩形.
参考答案
一.选择题
1.D
2.C
3.
C
4.
C.
5.
D.
6.
C.
7.
C.
8.
D.
9.
C.10.A
二.填空题(共5小题)
11.
45°
12.
50°
13.
65°
14.
2或2.4.
15.
.
三.解答题(共5小题)
16.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS).
(2)证明:∵E、F分别为边AB、CD的中点,
∴DF=DC,BE=AB,
又∵在?ABCD中,AB∥CD,AB=CD,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∵DB⊥BC,
∴∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边DC的中点,
∴BF=DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形.
17.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAE=∠ACF,∠CFO=∠AEO,
在△AOE和△COF中,,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:连接OB,如图所示:
∵BF=BE,OE=OF,
∴BO⊥EF,
由(1)知,△AOE≌△COF,
∴OA=OC,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BO=AC=OA,
∴∠BAC=∠OBA,
又∠BEF=2∠BAC,
∴∠BEF=2∠OBE,
而Rt△OBE中,∠BEO+∠OBE=90°,
∴∠BAC=30°,
∴BC=AC=3,
∴AB==9.
18.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
19.
解:(1)如图:BE、CF即∠ABC和∠BCD的平分线,
(2)AF与DE相等.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∴∠AEB=∠EBC,
∵BE平分∠ABC,∴∠ABE=∠CBE,
∴∠ABE=∠AEB,∴AB=AE,
同理可得:DF=CD,
∴AE=DF,即AF+EF=DE+EF,∴AF=DE.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=AD,F是BC边的中点,
∴FC=BC=AD=DE,又∵DE∥FC,
∴四边形CEDF是平行四边形.
21.解:(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵∠AEC=∠AFC,∠AEC+∠AEB=∠AFC+∠AFD=180°,
∴∠AEB=∠AFD,
∵AE=AF,
∴△AEB≌△AFD(AAS),
∴AB=AD,BE=DF,
∴平行四边形ABCD是菱形,
∴BC=DC,
∴EC=FC,
∴四边形AECF是筝形.
(2)如图∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS),
∴S△ABC=S△ADC,
过点B作BH⊥AC,垂足为H,
在Rt△ABH中,BH2=AB2﹣AH2=262﹣AH2,
在Rt△CBH中,BH2=CB2﹣CH2=252﹣(17﹣AH)2,
∴262﹣AH2=252﹣(17﹣AH)2,
∴AH=10,
∴BH==24,
∴S△ABC=×17×24=204.∴筝形ABCD的面积=2S△ABC=408.
22.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
23.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,∥ABO=∠OBC=30°,
∴AO=AB=6,
∴OB=AB?cos30°=6,
∴BD=2BO=12.
(2)①∵四边形ABCD是菱形,
∴AB∥CD,BO=OD,
∴∠EBO=∠GDO
∵∠BOE=∠DOG,
∴△EOB≌△GOD,
∴EO=GO,同理可得HO=FO,
∴四边形EFGH是平行四边形.
②a、当点E、H都在AB上时,四边形EFGH是矩形,作∠EOH的平分线OM,
∵OE=OH,
∴OM⊥EH.
∴∠MOB=90°﹣∠ABO=60°,
∵∠MOE=∠EOH=15°,
∴∠EOB=∠MOB﹣∠MOE=45°,作EN⊥OB于N.设ON=EN=x,则NB=x,
∵OB=6,
∴x+x=6,
∴x=9﹣3,
∴BE=2EN=18﹣6,
∴t=18﹣6时,四边形EFGH是矩形.
b、当点E在AB上,点H在AD上,四边形EFGH是矩形.
由菱形和矩形都是轴对称图形可知,∠AOE=∠AOH=15°,
∴∠EOB=90°﹣15°=75°,
∵∠ABO=30°,
∴∠BEO=180°﹣∠EOB﹣∠ABO=75°,
∴∠BEO=∠BOE,
∴BE=BO=6,
∴t=6时,四边形EFGH是矩形.
c、当点E、H都在AD上时,四边形EFGH是矩形.
由b同理可证:DE=DO=6,
∴AB+AE=AB+AD﹣DE=24﹣6
∴t=24﹣6时,四边形EFGH是矩形.
d、当点E在AD上,点H在DC上,四边形EFGH是矩形.
由菱形、矩形都是轴对称图形可知,∠DOE=∠HOE=15°,
∴∠EOA=90°﹣15°=75°,
∵∠OAD=60°,过点O作OK⊥AD,
∴∠AOK=90°﹣∠OAD=30°,
∴∠KOE=75°﹣30°=45°,
∴KE=OK,
∴AE=AK+KE=3+3,
∴BA+AE=15+3,
∴t=15+3,
∴t=15+3时,四边形EFGH是矩形.
综上所述,t为18﹣6,6,24﹣6,15+3时,四边形EFGH是矩形.
D
