2020-2021学年高中数学新人教A版必修第一册 交集和并集 课件(33张)
文档属性
| 名称 | 2020-2021学年高中数学新人教A版必修第一册 交集和并集 课件(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 667.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
第1课时 交集和并集
激趣诱思
知识点拨
公务员,是指在各级政府机关中,行使国家行政职权,执行国家公务的人员.每年都有很多人报名参加考试,常出现一个岗位若干人争夺的局面.
2020国家公务员考试报考条件中规定,报考人员应符合以下条件(摘录):(1)具有中华人民共和国国籍;(2)18周岁以上、35周岁以下(1983年10月至2001年10月期间出生),2020年应届硕士研究生和博士研究生(非在职)人员年龄可放宽到40周岁以下(1978年10月以后出生);……(7)具有大学专科及以上文化程度.
根据以上条件,哪些人可以报名参加公务员考试呢?
激趣诱思
知识点拨
一、交集
名师点析求两个集合的交集,结果还是一个集合,是由集合A与B的所有公共元素组成的集合.当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.
所有
{x|x∈A,且x∈B}
激趣诱思
知识点拨
微练习
(1)已知集合A={1,3,5,6,7},B={2,4,5,6,8},则A∩B= .?
(2)(2019全国Ⅱ)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )
A.(-1,+∞) B.(-∞,2)
C.(-1,2)
D.?
(3)已知集合A={-1,0,1,2,3},B={x|-2≤x≤2},那么A∩B=( )
A.{-1,0,1}
B.{-1,0,1,2}
C.{-1,0,1,2,3}
D.{x|-2≤x≤2}
答案:
(1){5,6} (2)
C
(3)B
激趣诱思
知识点拨
二、并集
所有
或
或
激趣诱思
知识点拨
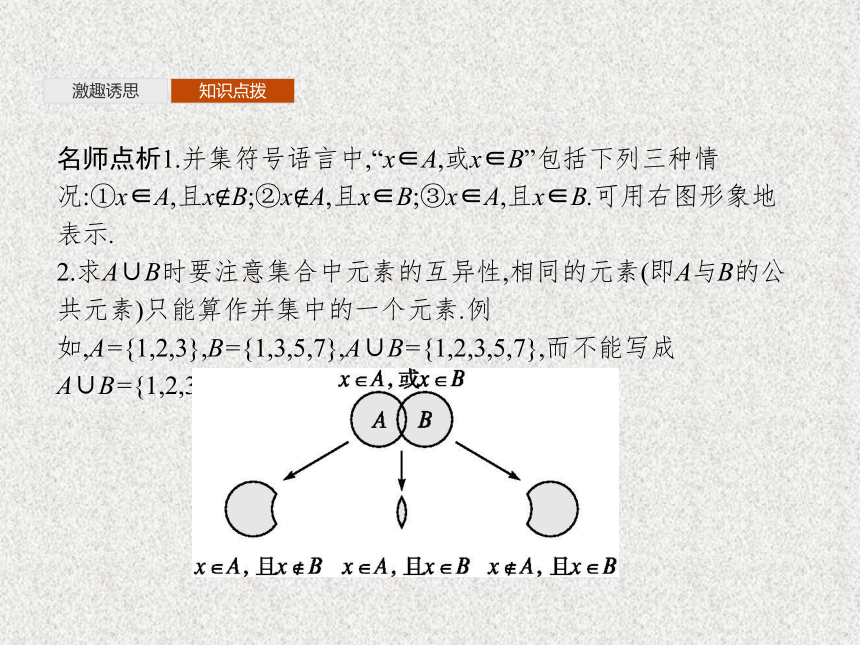
名师点析1.并集符号语言中,“x∈A,或x∈B”包括下列三种情况:①x∈A,且x?B;②x?A,且x∈B;③x∈A,且x∈B.可用右图形象地表示.
2.求A∪B时要注意集合中元素的互异性,相同的元素(即A与B的公共元素)只能算作并集中的一个元素.例如,A={1,2,3},B={1,3,5,7},A∪B={1,2,3,5,7},而不能写成A∪B={1,2,3,1,3,5,7}.
激趣诱思
知识点拨
微练习
(1)设集合A={1,3},集合B={1,2,4,5},则集合A∪B=( )
A.{1,3,1,2,4,5}
B.{1}
C.{1,2,3,4,5}
D.{2,3,4,5}
(2)已知集合A={x|x>-2},B={x|x≥1},则A∪B=( )
A.{x|x>-2}
B.{x|-2C.{x|x≤-2}
D.{x|x≥1}
(3)已知集合A={1,3,m},B={3,4},A∪B={1,2,3,4},则实数m= .?
答案:
(1)
C (2)A (3)2
探究一
探究二
探究三
素养形成
当堂检测
集合的交集与并集运算
例1(1)设集合A={x|x2-2x-3=0},B={x|x2=1},则A∪B=( )
A.{1}
B.{1,3}
C.{-1,1,3}
D.{-1,1}
(2)已知集合A={x|x<2},B={x≥1},则A∪B=( )
A.{x|x<2}
B.{x|1≤x<2}
C.{x|x≥1}
D.R
分析(1)先解一元二次方程得集合A,B,再根据集合并集的定义求结果;(2)用数轴表示集合A,B,根据定义求解.
解析:(1)A={-1,3},B={-1,1},A∪B={-1,1,3}.
(2)在数轴上表示出集合A,B,则
则A∪B=R.
答案:
(1)
C (2)D
探究一
探究二
探究三
素养形成
当堂检测
变式训练1(1)已知集合A={x∈N|1≤x≤3},B={2,3,4,5},则A∪B=( )
A.{2,3}
B.{2,3,4,5}
C.{2}
D.{1,2,3,4,5}
(2)设集合A={x∈N+|x≤2},B={2,6},则A∪B=( )
A.{2}
B.{2,6}
C.{1,2,6}
D.{0,1,2,6}
答案:
(1)
D (2)C
探究一
探究二
探究三
素养形成
当堂检测
例2(1)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B=( )
A.{3}
B.{5}
C.{3,5}
D.{1,2,3,4,5,7}
(2)设集合M={x|-3A.[1,2)
B.[1,2]
C.(2,3]
D.[2,3]
(3)(2019天津)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=( )
A.{2}
B.{2,3}
C.{-1,2,3}
D.{1,2,3,4}
答案:
(1)
C (2)
A (3)
D
探究一
探究二
探究三
素养形成
当堂检测
解析:(1)直接由交集定义可得A∩B={3,5};
(2)在数轴上表示集合M,N,如图:
∴M∩N={x|1≤x<2}.
(3)A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
求两个集合交集、并集的方法技巧
当求两个集合的并集、交集时,对于用描述法给出的集合,首先明确集合中的元素,其次将两个集合化为最简形式;对于连续的数集常借助于数轴写出结果,此时要注意数轴上方所有“线”下面的实数组成了并集,数轴上方“双线”(即公共部分)下面的实数组成了交集,此时要注意当端点不在集合中时,应用空心点表示;对于用列举法给出的集合,则依据并集、交集的含义,可直接观察或借助于Venn图写出结果.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2若集合M={x∈R|-3A.{0}
B.{-1,0}
C.{-1,0,1}
D.{-2,-1,0,1,2}
答案:B
解析:N={-1,0,1,2},M={x∈R|-3探究一
探究二
探究三
素养形成
当堂检测
已知集合的交集、并集求参数
例3已知a∈R,集合A={-4,2a-1,a2},B={a-5,1-a,9}.若9∈A∩B,则实数a的值为 .?
分析9∈A∩B说明9∈A,通过分类讨论建立关于a的方程求解,注意求出a的值后要代入集合A,B中,看是否满足集合中元素的互异性.
解析:∵9∈A∩B,∴9∈A,且9∈B,
∴2a-1=9或a2=9,解得a=5或a=±3.
当a=5时,A={-4,9,25},B={0,-4,9},符合题意;
当a=3时,A={-4,5,9},B={-2,-2,9},集合B不满足集合中元素的互异性,故a≠3;
当a=-3时,A={-4,-7,9},B={-8,4,9},符合题意.
综上可得实数a的值为5或-3.
答案:
5或-3
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
已知两个有限集运算结果求参数值的方法
对于这类已知两个有限集的运算结果求参数值的问题,一般先用观察法得到不同集合中元素之间的关系,再列方程求解.另外,在处理有关含参数的集合问题时,要注意对求解结果进行检验,检验求解结果是否满足集合中元素的有关特性,尤其是互异性.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究例3中,将“9∈A∩B”改为“A∩B={9}”,其余条件不变,求实数a的值及A∪B.
解:∵A∩B={9},∴9∈A.
∴2a-1=9或a2=9,解得a=5或a=±3.
当a=5时,A={-4,9,25},B={0,-4,9},由于A∩B={-4,9},不符合题意,故a≠5;
当a=3时,A={-4,5,9},B={-2,-2,9},集合不满足集合中元素的互异性,故a≠3;
当a=-3时,A={-4,-7,9},B={-8,4,9},且A∩B={9},符合题意.
综上可得a=-3.此时A∪B={-8,-4,-7,4,9}.
探究一
探究二
探究三
素养形成
当堂检测
例4集合A={x|-1(1)若A∩B=?,求a的取值范围;
(2)若A∪B={x|x<1},求a的取值范围.
分析利用数轴把集合A,B表示出来,根据题目条件,利用数形结合的方法列出关于参数a满足的不等式,求解时需注意等号能否取得.
探究一
探究二
探究三
素养形成
当堂检测
解:(1)A={x|-1∴数轴上点x=a在点x=-1左侧,且包含点x=-1,
∴a的取值范围为a≤-1.
(2)A={x|-1∴数轴上点x=a在点x=-1和点x=1之间,不包含点x=-1,但包含点x=1.∴a的取值范围为-1探究一
探究二
探究三
素养形成
当堂检测
反思感悟
已知集合运算求参数的思路
此类问题常借助数轴解决,首先根据集合间的关系画出数轴,然后根据数轴列出关于参数的不等式(组)求解,特别要注意端点值的取舍.当集合的元素离散时,常借助集合的关系列关于参数的方程(组)求解,但求解后要代入检验是否符合题意.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究例4(1)中,把“A∩B=?”改为“A∩B≠?”,求a的取值范围.
解:利用数轴(略)表示出两个集合,数形结合知,要使A∩B≠?,需数轴上点x=a在点x=-1右侧且不包含点x=-1,所以a的取值范围为a>-1.
探究一
探究二
探究三
素养形成
当堂检测
集合的交集、并集性质的应用
例5设集合M={x|-2分析把M∪N=M转化为N?M,利用数轴表示出两个集合,建立端点间的不等关系式求解.
综上可知,实数t的取值范围是{t|t≤2}.
答案:{t|t≤2}
探究一
探究二
探究三
素养形成
当堂检测
延伸探究将例5条件中“M∪N=M”改为“M∩N=M”,其余不变,求实数t的取值范围.
解:由M∩N=M,得M?N,故N≠?.用数轴(略)表示两个集合,
故实数t的取值范围为t≥4.
探究一
探究二
探究三
素养形成
当堂检测
例6设集合A={x|x2-2x=0},B={x|x2-2ax+a2-a=0}.
(1)若A∩B=B,求a的取值范围;
(2)若A∪B=B,求a的值.
分析先化简集合A,B,再由已知条件得A∩B=B和A∪B=B,转化为集合A,B的包含关系,分类讨论求a的值或取值范围.
探究一
探究二
探究三
素养形成
当堂检测
解:由x2-2x=0,得x=0或x=2.∴A={0,2}.
(1)∵A∩B=B,∴B?A,B=?,{0},{2},{0,2}.
当B=?时,Δ=4a2-4(a2-a)=4a<0,∴a<0;
综上所述,得a的取值范围是{a|a=1或a≤0}.
(2)∵A∪B=B,∴A?B.
∵A={0,2},而B中方程至多有两个根,
∴A=B,由(1)知a=1.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
利用交集、并集运算求参数的思路
(1)涉及A∩B=B或A∪B=A的问题,可利用集合的运算性质,转化为相关集合之间的关系求解,要注意空集的特殊性.
(2)将集合中的运算关系转化为两个集合之间的关系.若集合中的元素能一一列举,则可用观察法得到不同集合中元素之间的关系,要注意集合中元素的互异性;与不等式有关的集合,则可利用数轴得到不同集合之间的关系.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3已知集合M={x|2x-4=0},集合N={x|x2-3x+m=0},
(1)当m=2时,求M∩N,M∪N;
(2)当M∩N=M时,求实数m的值.
解:(1)由题意得M={2}.
当m=2时,N={x|x2-3x+2=0}={1,2},
∴M∩N={2},M∪N={1,2}.
(2)∵M∩N=M,∴M?N.∵M={2},∴2∈N,
∴2是关于x的方程x2-3x+m=0的解,
即4-6+m=0,解得m=2.
探究一
探究二
探究三
素养形成
当堂检测
分类讨论思想在集合运算中的应用
分类讨论就是分别归类再进行讨论的意思,数学中的分类过程就是对事件共性的抽象过程.解题时要明确为什么分类,如何分类,如何确定分类的标准.应用时,首先要审清题意,认真分析可能产生的不同因素.进行讨论时要确定分类的标准,每一次分类只能按照一个标准来分,不能重复也不能遗漏.
探究一
探究二
探究三
素养形成
当堂检测
典例
设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
解:(1)集合A={x|x2-3x+2=0}={1,2},
若A∩B={2},则x=2是方程x2+2(a+1)x+a2-5=0的实数根,可得a2+4a+3=0,解得a=-3或a=-1.
当a=-3时,B={2};当a=-1时,B={-2,2},均满足A∩B={2}.综上,实数a的值为a=-3或a=-1.
(2)A={x|x2-3x+2=0}={1,2},
B={x|x2+2(a+1)x+(a2-5)=0},
对应的Δ=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B?A.
探究一
探究二
探究三
素养形成
当堂检测
①当Δ<0,即a<-3时,B=?,满足条件;
②当Δ=0,即a=-3时,B={2},满足条件;
③当Δ>0,即a>-3时,只有B={1,2},才能满足条件,
由一元二次方程根与系数的关系,得1+2=-2(a+1),且1×2=a2-5.
方法点睛
将条件转化为两个集合的包含关系,因为集合B是由含参的一元二次方程的解组成的,所以应按其解的个数分类讨论.尤其不要忽略无解的情况,即B为空集的情况.
探究一
探究二
探究三
素养形成
当堂检测
1.设集合A={x∈N+|-1≤x≤2},B={2,3},则A∪B=( )
A.{-1,0,1,2,3}
B.{1,2,3}
C.[-1,2]
D.[-1,3]
答案:B
解析:集合A={1,2},B={2,3},则A∪B={1,2,3}.
2.已知集合A={x|-3A.{x|x<1}
B.{x|x<3}
C.{x|-3D.{x|-3答案:C
探究一
探究二
探究三
素养形成
当堂检测
3.已知集合A={0,1},B={a-2,2}.若A∩B={1},则A∪B=( )
A.{0,1,2}
B.{1}
C.{0,1,2,3}
D.{1,2}
答案:A
解析:由A∩B={1},得1=a-2,所以a=3.则B={1,2}.所以A∪B={0,1,2}.
4.已知集合A={0,1,2,8},B={-1,1,6,8},那么A∩B= .?
答案:{1,8}
探究一
探究二
探究三
素养形成
当堂检测
5.已知集合A={x|m-2(1)若m=1,求A∪B;
(2)若A∩B=A,求实数m的取值范围.
解:(1)由m=1,得A={x|-1∴A∪B={x|-1(2)∵A∩B=A,∴A?B.显然A≠?.
第1课时 交集和并集
激趣诱思
知识点拨
公务员,是指在各级政府机关中,行使国家行政职权,执行国家公务的人员.每年都有很多人报名参加考试,常出现一个岗位若干人争夺的局面.
2020国家公务员考试报考条件中规定,报考人员应符合以下条件(摘录):(1)具有中华人民共和国国籍;(2)18周岁以上、35周岁以下(1983年10月至2001年10月期间出生),2020年应届硕士研究生和博士研究生(非在职)人员年龄可放宽到40周岁以下(1978年10月以后出生);……(7)具有大学专科及以上文化程度.
根据以上条件,哪些人可以报名参加公务员考试呢?
激趣诱思
知识点拨
一、交集
名师点析求两个集合的交集,结果还是一个集合,是由集合A与B的所有公共元素组成的集合.当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.
所有
{x|x∈A,且x∈B}
激趣诱思
知识点拨
微练习
(1)已知集合A={1,3,5,6,7},B={2,4,5,6,8},则A∩B= .?
(2)(2019全国Ⅱ)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )
A.(-1,+∞) B.(-∞,2)
C.(-1,2)
D.?
(3)已知集合A={-1,0,1,2,3},B={x|-2≤x≤2},那么A∩B=( )
A.{-1,0,1}
B.{-1,0,1,2}
C.{-1,0,1,2,3}
D.{x|-2≤x≤2}
答案:
(1){5,6} (2)
C
(3)B
激趣诱思
知识点拨
二、并集
所有
或
或
激趣诱思
知识点拨
名师点析1.并集符号语言中,“x∈A,或x∈B”包括下列三种情况:①x∈A,且x?B;②x?A,且x∈B;③x∈A,且x∈B.可用右图形象地表示.
2.求A∪B时要注意集合中元素的互异性,相同的元素(即A与B的公共元素)只能算作并集中的一个元素.例如,A={1,2,3},B={1,3,5,7},A∪B={1,2,3,5,7},而不能写成A∪B={1,2,3,1,3,5,7}.
激趣诱思
知识点拨
微练习
(1)设集合A={1,3},集合B={1,2,4,5},则集合A∪B=( )
A.{1,3,1,2,4,5}
B.{1}
C.{1,2,3,4,5}
D.{2,3,4,5}
(2)已知集合A={x|x>-2},B={x|x≥1},则A∪B=( )
A.{x|x>-2}
B.{x|-2
D.{x|x≥1}
(3)已知集合A={1,3,m},B={3,4},A∪B={1,2,3,4},则实数m= .?
答案:
(1)
C (2)A (3)2
探究一
探究二
探究三
素养形成
当堂检测
集合的交集与并集运算
例1(1)设集合A={x|x2-2x-3=0},B={x|x2=1},则A∪B=( )
A.{1}
B.{1,3}
C.{-1,1,3}
D.{-1,1}
(2)已知集合A={x|x<2},B={x≥1},则A∪B=( )
A.{x|x<2}
B.{x|1≤x<2}
C.{x|x≥1}
D.R
分析(1)先解一元二次方程得集合A,B,再根据集合并集的定义求结果;(2)用数轴表示集合A,B,根据定义求解.
解析:(1)A={-1,3},B={-1,1},A∪B={-1,1,3}.
(2)在数轴上表示出集合A,B,则
则A∪B=R.
答案:
(1)
C (2)D
探究一
探究二
探究三
素养形成
当堂检测
变式训练1(1)已知集合A={x∈N|1≤x≤3},B={2,3,4,5},则A∪B=( )
A.{2,3}
B.{2,3,4,5}
C.{2}
D.{1,2,3,4,5}
(2)设集合A={x∈N+|x≤2},B={2,6},则A∪B=( )
A.{2}
B.{2,6}
C.{1,2,6}
D.{0,1,2,6}
答案:
(1)
D (2)C
探究一
探究二
探究三
素养形成
当堂检测
例2(1)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B=( )
A.{3}
B.{5}
C.{3,5}
D.{1,2,3,4,5,7}
(2)设集合M={x|-3
B.[1,2]
C.(2,3]
D.[2,3]
(3)(2019天津)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=( )
A.{2}
B.{2,3}
C.{-1,2,3}
D.{1,2,3,4}
答案:
(1)
C (2)
A (3)
D
探究一
探究二
探究三
素养形成
当堂检测
解析:(1)直接由交集定义可得A∩B={3,5};
(2)在数轴上表示集合M,N,如图:
∴M∩N={x|1≤x<2}.
(3)A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
求两个集合交集、并集的方法技巧
当求两个集合的并集、交集时,对于用描述法给出的集合,首先明确集合中的元素,其次将两个集合化为最简形式;对于连续的数集常借助于数轴写出结果,此时要注意数轴上方所有“线”下面的实数组成了并集,数轴上方“双线”(即公共部分)下面的实数组成了交集,此时要注意当端点不在集合中时,应用空心点表示;对于用列举法给出的集合,则依据并集、交集的含义,可直接观察或借助于Venn图写出结果.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2若集合M={x∈R|-3
B.{-1,0}
C.{-1,0,1}
D.{-2,-1,0,1,2}
答案:B
解析:N={-1,0,1,2},M={x∈R|-3
探究二
探究三
素养形成
当堂检测
已知集合的交集、并集求参数
例3已知a∈R,集合A={-4,2a-1,a2},B={a-5,1-a,9}.若9∈A∩B,则实数a的值为 .?
分析9∈A∩B说明9∈A,通过分类讨论建立关于a的方程求解,注意求出a的值后要代入集合A,B中,看是否满足集合中元素的互异性.
解析:∵9∈A∩B,∴9∈A,且9∈B,
∴2a-1=9或a2=9,解得a=5或a=±3.
当a=5时,A={-4,9,25},B={0,-4,9},符合题意;
当a=3时,A={-4,5,9},B={-2,-2,9},集合B不满足集合中元素的互异性,故a≠3;
当a=-3时,A={-4,-7,9},B={-8,4,9},符合题意.
综上可得实数a的值为5或-3.
答案:
5或-3
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
已知两个有限集运算结果求参数值的方法
对于这类已知两个有限集的运算结果求参数值的问题,一般先用观察法得到不同集合中元素之间的关系,再列方程求解.另外,在处理有关含参数的集合问题时,要注意对求解结果进行检验,检验求解结果是否满足集合中元素的有关特性,尤其是互异性.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究例3中,将“9∈A∩B”改为“A∩B={9}”,其余条件不变,求实数a的值及A∪B.
解:∵A∩B={9},∴9∈A.
∴2a-1=9或a2=9,解得a=5或a=±3.
当a=5时,A={-4,9,25},B={0,-4,9},由于A∩B={-4,9},不符合题意,故a≠5;
当a=3时,A={-4,5,9},B={-2,-2,9},集合不满足集合中元素的互异性,故a≠3;
当a=-3时,A={-4,-7,9},B={-8,4,9},且A∩B={9},符合题意.
综上可得a=-3.此时A∪B={-8,-4,-7,4,9}.
探究一
探究二
探究三
素养形成
当堂检测
例4集合A={x|-1
(2)若A∪B={x|x<1},求a的取值范围.
分析利用数轴把集合A,B表示出来,根据题目条件,利用数形结合的方法列出关于参数a满足的不等式,求解时需注意等号能否取得.
探究一
探究二
探究三
素养形成
当堂检测
解:(1)A={x|-1
∴a的取值范围为a≤-1.
(2)A={x|-1
探究二
探究三
素养形成
当堂检测
反思感悟
已知集合运算求参数的思路
此类问题常借助数轴解决,首先根据集合间的关系画出数轴,然后根据数轴列出关于参数的不等式(组)求解,特别要注意端点值的取舍.当集合的元素离散时,常借助集合的关系列关于参数的方程(组)求解,但求解后要代入检验是否符合题意.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究例4(1)中,把“A∩B=?”改为“A∩B≠?”,求a的取值范围.
解:利用数轴(略)表示出两个集合,数形结合知,要使A∩B≠?,需数轴上点x=a在点x=-1右侧且不包含点x=-1,所以a的取值范围为a>-1.
探究一
探究二
探究三
素养形成
当堂检测
集合的交集、并集性质的应用
例5设集合M={x|-2
综上可知,实数t的取值范围是{t|t≤2}.
答案:{t|t≤2}
探究一
探究二
探究三
素养形成
当堂检测
延伸探究将例5条件中“M∪N=M”改为“M∩N=M”,其余不变,求实数t的取值范围.
解:由M∩N=M,得M?N,故N≠?.用数轴(略)表示两个集合,
故实数t的取值范围为t≥4.
探究一
探究二
探究三
素养形成
当堂检测
例6设集合A={x|x2-2x=0},B={x|x2-2ax+a2-a=0}.
(1)若A∩B=B,求a的取值范围;
(2)若A∪B=B,求a的值.
分析先化简集合A,B,再由已知条件得A∩B=B和A∪B=B,转化为集合A,B的包含关系,分类讨论求a的值或取值范围.
探究一
探究二
探究三
素养形成
当堂检测
解:由x2-2x=0,得x=0或x=2.∴A={0,2}.
(1)∵A∩B=B,∴B?A,B=?,{0},{2},{0,2}.
当B=?时,Δ=4a2-4(a2-a)=4a<0,∴a<0;
综上所述,得a的取值范围是{a|a=1或a≤0}.
(2)∵A∪B=B,∴A?B.
∵A={0,2},而B中方程至多有两个根,
∴A=B,由(1)知a=1.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
利用交集、并集运算求参数的思路
(1)涉及A∩B=B或A∪B=A的问题,可利用集合的运算性质,转化为相关集合之间的关系求解,要注意空集的特殊性.
(2)将集合中的运算关系转化为两个集合之间的关系.若集合中的元素能一一列举,则可用观察法得到不同集合中元素之间的关系,要注意集合中元素的互异性;与不等式有关的集合,则可利用数轴得到不同集合之间的关系.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3已知集合M={x|2x-4=0},集合N={x|x2-3x+m=0},
(1)当m=2时,求M∩N,M∪N;
(2)当M∩N=M时,求实数m的值.
解:(1)由题意得M={2}.
当m=2时,N={x|x2-3x+2=0}={1,2},
∴M∩N={2},M∪N={1,2}.
(2)∵M∩N=M,∴M?N.∵M={2},∴2∈N,
∴2是关于x的方程x2-3x+m=0的解,
即4-6+m=0,解得m=2.
探究一
探究二
探究三
素养形成
当堂检测
分类讨论思想在集合运算中的应用
分类讨论就是分别归类再进行讨论的意思,数学中的分类过程就是对事件共性的抽象过程.解题时要明确为什么分类,如何分类,如何确定分类的标准.应用时,首先要审清题意,认真分析可能产生的不同因素.进行讨论时要确定分类的标准,每一次分类只能按照一个标准来分,不能重复也不能遗漏.
探究一
探究二
探究三
素养形成
当堂检测
典例
设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
解:(1)集合A={x|x2-3x+2=0}={1,2},
若A∩B={2},则x=2是方程x2+2(a+1)x+a2-5=0的实数根,可得a2+4a+3=0,解得a=-3或a=-1.
当a=-3时,B={2};当a=-1时,B={-2,2},均满足A∩B={2}.综上,实数a的值为a=-3或a=-1.
(2)A={x|x2-3x+2=0}={1,2},
B={x|x2+2(a+1)x+(a2-5)=0},
对应的Δ=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B?A.
探究一
探究二
探究三
素养形成
当堂检测
①当Δ<0,即a<-3时,B=?,满足条件;
②当Δ=0,即a=-3时,B={2},满足条件;
③当Δ>0,即a>-3时,只有B={1,2},才能满足条件,
由一元二次方程根与系数的关系,得1+2=-2(a+1),且1×2=a2-5.
方法点睛
将条件转化为两个集合的包含关系,因为集合B是由含参的一元二次方程的解组成的,所以应按其解的个数分类讨论.尤其不要忽略无解的情况,即B为空集的情况.
探究一
探究二
探究三
素养形成
当堂检测
1.设集合A={x∈N+|-1≤x≤2},B={2,3},则A∪B=( )
A.{-1,0,1,2,3}
B.{1,2,3}
C.[-1,2]
D.[-1,3]
答案:B
解析:集合A={1,2},B={2,3},则A∪B={1,2,3}.
2.已知集合A={x|-3
B.{x|x<3}
C.{x|-3
探究一
探究二
探究三
素养形成
当堂检测
3.已知集合A={0,1},B={a-2,2}.若A∩B={1},则A∪B=( )
A.{0,1,2}
B.{1}
C.{0,1,2,3}
D.{1,2}
答案:A
解析:由A∩B={1},得1=a-2,所以a=3.则B={1,2}.所以A∪B={0,1,2}.
4.已知集合A={0,1,2,8},B={-1,1,6,8},那么A∩B= .?
答案:{1,8}
探究一
探究二
探究三
素养形成
当堂检测
5.已知集合A={x|m-2
(2)若A∩B=A,求实数m的取值范围.
解:(1)由m=1,得A={x|-1
