2020-2021学年 沪教版(上海)七年级第二学期数学期末复习综合测试题(word版无答案)
文档属性
| 名称 | 2020-2021学年 沪教版(上海)七年级第二学期数学期末复习综合测试题(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 07:37:21 | ||
图片预览

文档简介
1061720010744200123190000期末复习综合测试题
(满分120分;时间:90分钟)
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
1. 在下列各数中,无理数是( )
A.4 B.π3 C.227 D.38?
2. 已知x-2+y+8=0,则x+y的值为( )
A.10 B.不能确定 C.-6 D.-10?
3. 下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等;(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是( )
A.(1)(2)(4) B.(2)(3)(4) C.(1)(2)(3) D.(1)(2)(3)(4)?
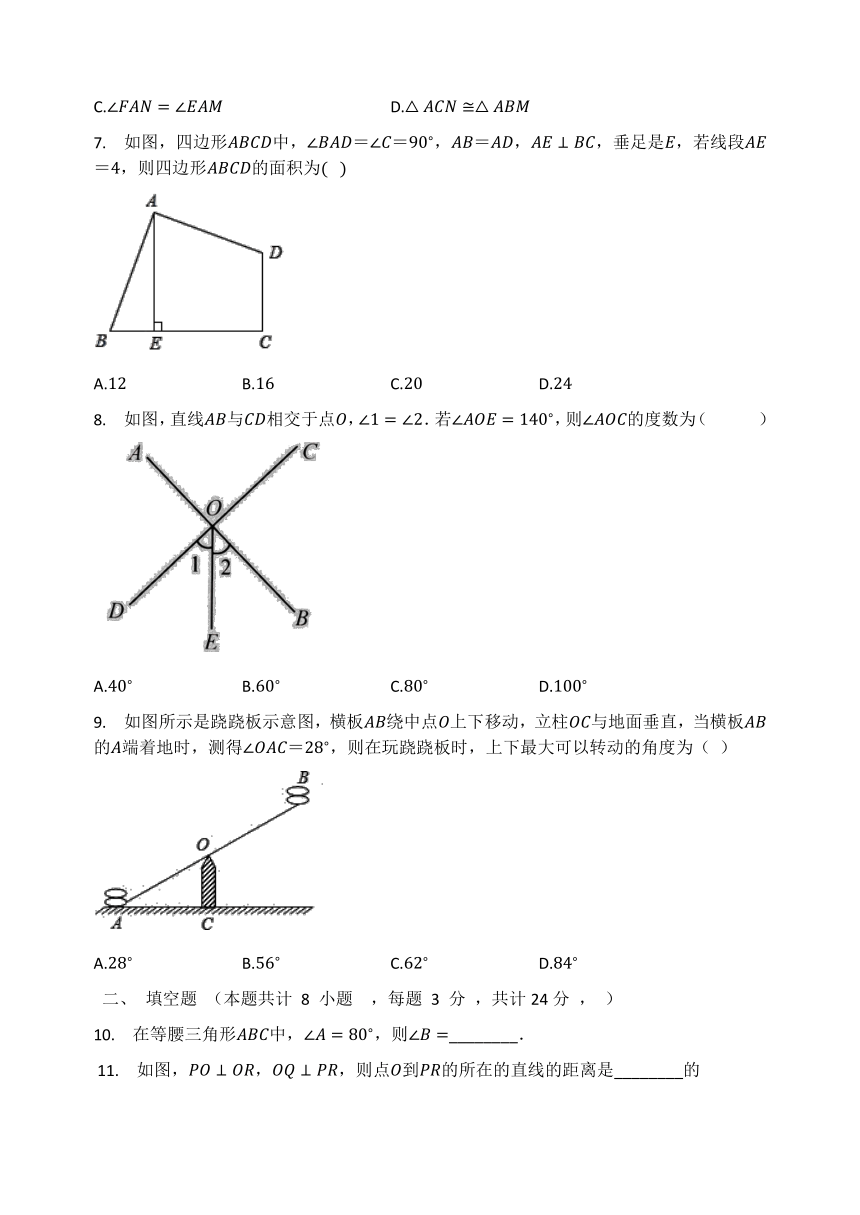
4. 如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC?△DFE(? ? ? ?)
A.BC=EF B.∠A=∠D C.AC?//?DF D.AC=DF?
5. 下列说法错误的是( )
A.在同一平面内,两条不平行的直线是相交线
B.与同一条直线平行的直线必平行
C.与同一条直线相交的直线必相交
D.过直线外一点有且只有一条直线平行于已知直线?
6. 如图,某班数学兴趣小组将两块全等的三角板叠放在一起,已知∠E=∠F=90?,AE=AF,经过探究得出以下结论,其中判断错误的是(? ? ? ? )
A.EM=FN B.AF?//?EB
C.∠FAN=∠EAM D.△ACN?△ABM?
7. 如图,四边形ABCD中,∠BAD=∠C=90?,AB=AD,AE⊥BC,垂足是E,若线段AE=4,则四边形ABCD的面积为(???)
A.12 B.16 C.20 D.24?
8. 如图,直线AB与CD相交于点O,∠1=∠2.若∠AOE=140?,则∠AOC的度数为(? ? ? ? )
A.40? B.60? C.80? D.100??
9. 如图所示是跷跷板示意图,横板AB绕中点O上下移动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=28?,则在玩跷跷板时,上下最大可以转动的角度为( )
A.28? B.56? C.62? D.84?
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
10. 在等腰三角形ABC中,∠A=80?,则∠B=________.
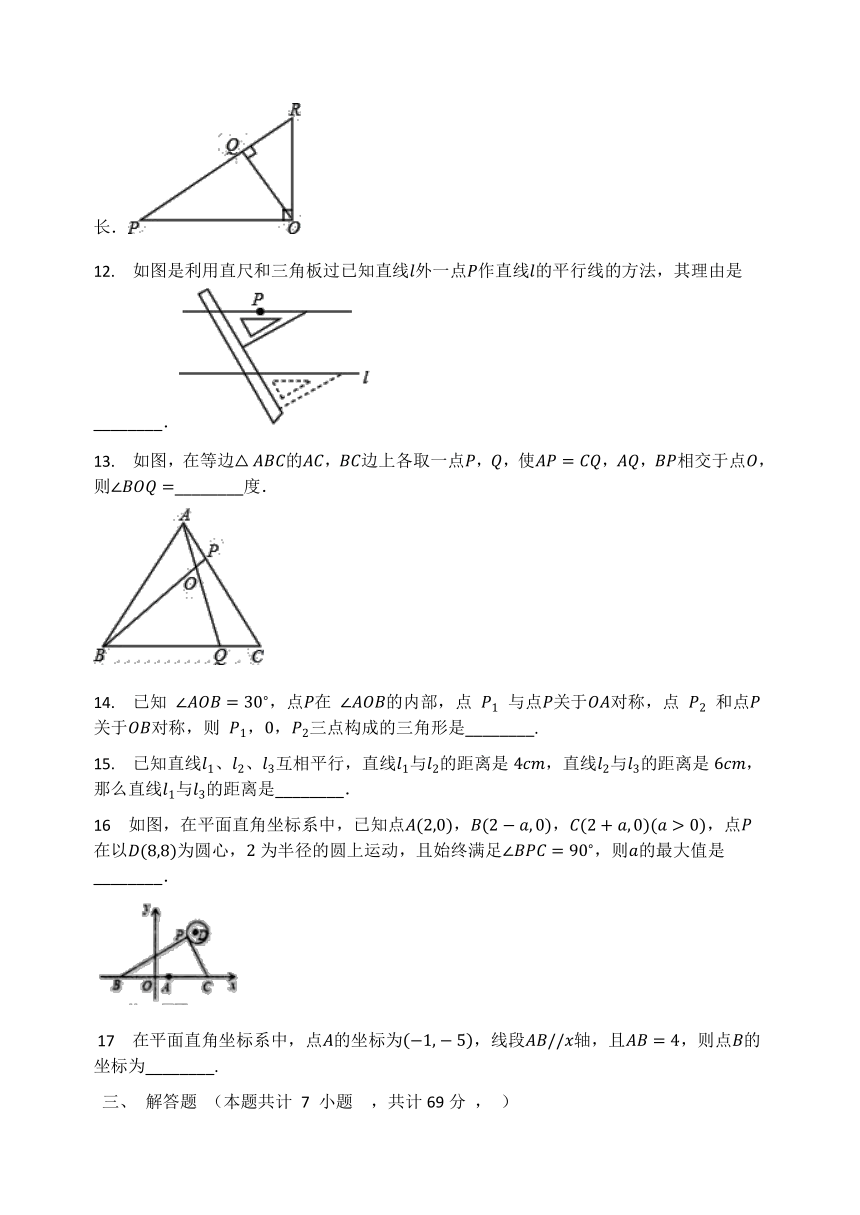
?11. 如图,PO⊥OR,OQ⊥PR,则点O到PR的所在的直线的距离是________的长.
12. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是________. ?
13. 如图,在等边△ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O,则∠BOQ=________度.
?
14. 已知 ∠AOB=30?,点P在 ∠AOB的内部,点 P1 与点P关于OA对称,点 P2 和点P关于OB对称,则 P1,0,P2三点构成的三角形是________. ?
15. 已知直线l1、l2、l3互相平行,直线l1与l2的距离是4cm,直线l2与l3的距离是6cm,那么直线l1与l3的距离是________. ??
16 如图,在平面直角坐标系中,已知点A(2,0),B(2-a,0),C(2+a,0)(a>0),点P在以D(8,8)为圆心,2为半径的圆上运动,且始终满足∠BPC=90?,则a的最大值是________.
?17 在平面直角坐标系中,点A的坐标为-1,-5,线段AB//x轴,且AB=4,则点B的坐标为________.
三、 解答题 (本题共计 7 小题 ,共计69分 , ) ?
18 如图,在△ABC中,AD是高,AE是角平分线,∠B=70?,∠DAE=18?,求∠C的度数.
?
19 如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30?,OP=8.
(1)射线OP与y轴正半轴的夹角为________.
(2)求点P的坐标.
?
20. 已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数,求c的长.
?
21 已知:如图所示,
(1)写出△ABC三个顶点的坐标;
(2)作出△ABC关于x轴对称的△A'B'C',并写出△A'B'C'三个顶点的坐标.
(3)作出△ABC关于y轴对称的△A''B''C'',并写出△A''B''C''三个顶点的坐标.
?
22 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,?2),B(3,?4),请在所给网格上按要求画整点四边形.
(1)在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.
(2)在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.
?
23 在△ABC中,∠C>∠B,AE平分∠BAC.
1如图(1),AD⊥BC于D,若∠C=75?,∠B=35?,求∠EAD;
2如图(1),AD⊥BC于D,猜想∠EAD与∠B,∠C有什么数量关系?请说明你的理由;
3如图(2),F为AE上一点,FD⊥BC于D,这时∠EFD与∠B、∠C又有什么数量关系?________;(不用证明)
4如图(3),F为AE的延长线上的一点,FD⊥BC于D,这时∠AFD与∠B、∠C又有什么数量关系?________.(不用证明)
?
24. 如图:在△ABC中,∠ACB=90?,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM,BN与MN三者之间有怎样数量关系?请说明理由.
(满分120分;时间:90分钟)
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
1. 在下列各数中,无理数是( )
A.4 B.π3 C.227 D.38?
2. 已知x-2+y+8=0,则x+y的值为( )
A.10 B.不能确定 C.-6 D.-10?
3. 下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等;(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是( )
A.(1)(2)(4) B.(2)(3)(4) C.(1)(2)(3) D.(1)(2)(3)(4)?
4. 如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC?△DFE(? ? ? ?)
A.BC=EF B.∠A=∠D C.AC?//?DF D.AC=DF?
5. 下列说法错误的是( )
A.在同一平面内,两条不平行的直线是相交线
B.与同一条直线平行的直线必平行
C.与同一条直线相交的直线必相交
D.过直线外一点有且只有一条直线平行于已知直线?
6. 如图,某班数学兴趣小组将两块全等的三角板叠放在一起,已知∠E=∠F=90?,AE=AF,经过探究得出以下结论,其中判断错误的是(? ? ? ? )
A.EM=FN B.AF?//?EB
C.∠FAN=∠EAM D.△ACN?△ABM?
7. 如图,四边形ABCD中,∠BAD=∠C=90?,AB=AD,AE⊥BC,垂足是E,若线段AE=4,则四边形ABCD的面积为(???)
A.12 B.16 C.20 D.24?
8. 如图,直线AB与CD相交于点O,∠1=∠2.若∠AOE=140?,则∠AOC的度数为(? ? ? ? )
A.40? B.60? C.80? D.100??
9. 如图所示是跷跷板示意图,横板AB绕中点O上下移动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=28?,则在玩跷跷板时,上下最大可以转动的角度为( )
A.28? B.56? C.62? D.84?
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
10. 在等腰三角形ABC中,∠A=80?,则∠B=________.
?11. 如图,PO⊥OR,OQ⊥PR,则点O到PR的所在的直线的距离是________的长.
12. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是________. ?
13. 如图,在等边△ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O,则∠BOQ=________度.
?
14. 已知 ∠AOB=30?,点P在 ∠AOB的内部,点 P1 与点P关于OA对称,点 P2 和点P关于OB对称,则 P1,0,P2三点构成的三角形是________. ?
15. 已知直线l1、l2、l3互相平行,直线l1与l2的距离是4cm,直线l2与l3的距离是6cm,那么直线l1与l3的距离是________. ??
16 如图,在平面直角坐标系中,已知点A(2,0),B(2-a,0),C(2+a,0)(a>0),点P在以D(8,8)为圆心,2为半径的圆上运动,且始终满足∠BPC=90?,则a的最大值是________.
?17 在平面直角坐标系中,点A的坐标为-1,-5,线段AB//x轴,且AB=4,则点B的坐标为________.
三、 解答题 (本题共计 7 小题 ,共计69分 , ) ?
18 如图,在△ABC中,AD是高,AE是角平分线,∠B=70?,∠DAE=18?,求∠C的度数.
?
19 如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30?,OP=8.
(1)射线OP与y轴正半轴的夹角为________.
(2)求点P的坐标.
?
20. 已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数,求c的长.
?
21 已知:如图所示,
(1)写出△ABC三个顶点的坐标;
(2)作出△ABC关于x轴对称的△A'B'C',并写出△A'B'C'三个顶点的坐标.
(3)作出△ABC关于y轴对称的△A''B''C'',并写出△A''B''C''三个顶点的坐标.
?
22 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,?2),B(3,?4),请在所给网格上按要求画整点四边形.
(1)在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.
(2)在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.
?
23 在△ABC中,∠C>∠B,AE平分∠BAC.
1如图(1),AD⊥BC于D,若∠C=75?,∠B=35?,求∠EAD;
2如图(1),AD⊥BC于D,猜想∠EAD与∠B,∠C有什么数量关系?请说明你的理由;
3如图(2),F为AE上一点,FD⊥BC于D,这时∠EFD与∠B、∠C又有什么数量关系?________;(不用证明)
4如图(3),F为AE的延长线上的一点,FD⊥BC于D,这时∠AFD与∠B、∠C又有什么数量关系?________.(不用证明)
?
24. 如图:在△ABC中,∠ACB=90?,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM,BN与MN三者之间有怎样数量关系?请说明理由.
同课章节目录
