北师大版九年级数学下册:1.5《锐角三角函数及应用》教案
文档属性
| 名称 | 北师大版九年级数学下册:1.5《锐角三角函数及应用》教案 |  | |
| 格式 | docx | ||
| 文件大小 | 79.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 17:56:09 | ||
图片预览

文档简介
《锐角三角函数及应用》教学设计
教材分析
“锐角三角函数”是《数学课程标准》中“空间与图形”领域的重要内容,初中阶段主要研究锐角三角函数、解直角三角形及运用三角函数解决与直角三角形有关的实际问题,是高中数学三角学的基础,起着承上启下的作用,因此这部分也是中考必考内容之一,在中考复习中必须给予重视,通过学习,学生进一步把形和数结合起来,提高了分析和解决问题的能力,因此,本节课的教学重点为:从实际问题中抽象出基本图形,掌握并灵活应用各种关系解直角三角形。
教学目标
1、掌握并灵活应用各种关系解直角三角形。
2、经历从实际情况中抽象出数学图形和数学符号的过程,感受方程的思想在锐角三角函数中的应用,积累数学建模的经验。
3、以历观察、讨论等数学活动过程,发展合情推理能力,能有条理地、清晰地阐述自己的观点。
4、体验数形之间的联系,注重数学思想的运用,培养学生分析问题解决问题的能力。
学情分析
九年级学生已经牢固掌握了勾股定理,三角形相似,也已经学习过锐角三角函数、特殊角度的三角函数值,在此基础上,解直角三角形难度并不大,但要达到熟练运用的程度还有一定困难,学生抽象概括能力也有,限,综合运用所学知识解决问题,将实际问题抽象为数学问题的能力都有待提高,因此,我认为本节课的教学难点是:从实际问题中抽象出基本图形,掌握并灵活应用各种关系解直角三角形。
教学过程
教学环节
教 师 活 动
学 生 活 动
设 计 意 图
一、
创设情境
二、
课前整理
复习回顾
三、
合用交流
探求新知
四、
发展思维
应用拓展
五、
归纳小结
内化升华
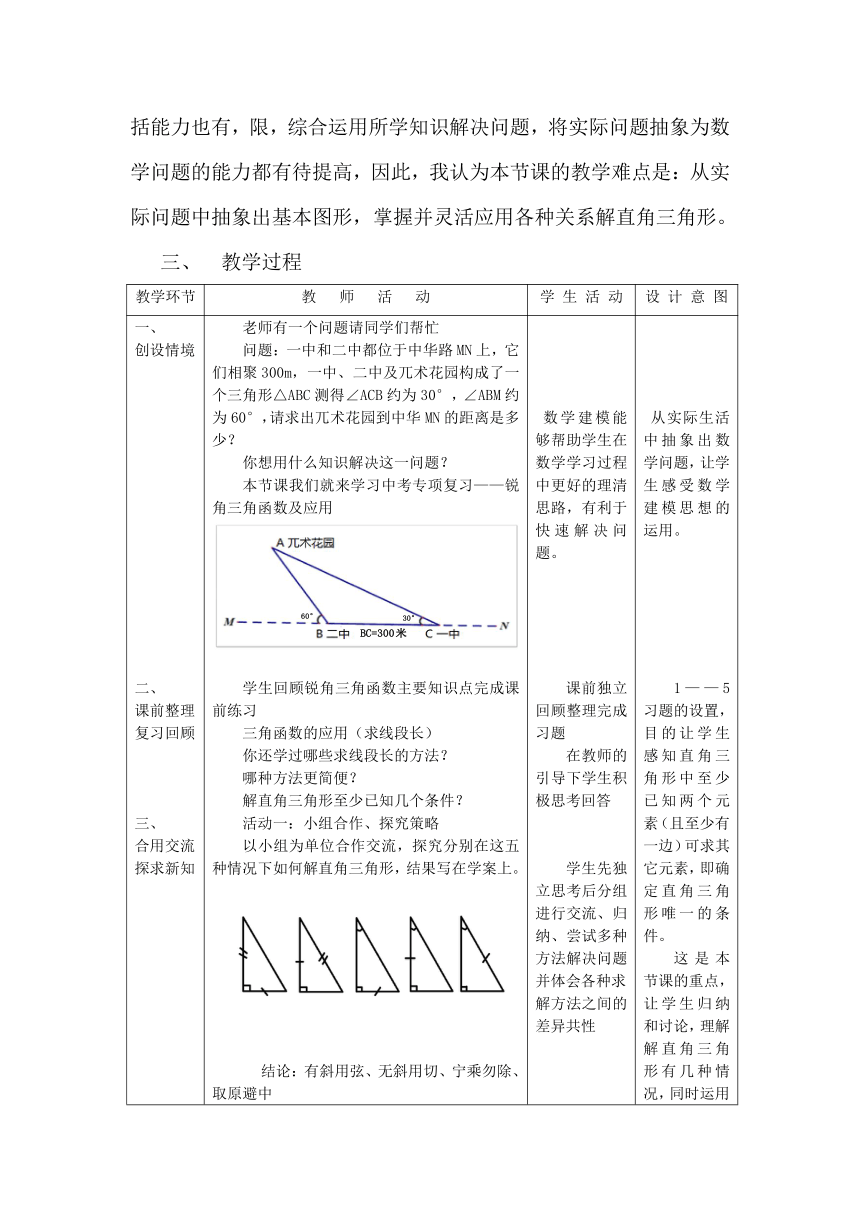
老师有一个问题请同学们帮忙
问题:一中和二中都位于中华路MN上,它们相聚300m,一中、二中及兀术花园构成了一个三角形△ABC测得∠ACB约为30°,∠ABM约为60°,请求出兀术花园到中华MN的距离是多少?
你想用什么知识解决这一问题?
本节课我们就来学习中考专项复习——锐角三角函数及应用
BC=300米
30°
60°
学生回顾锐角三角函数主要知识点完成课前练习
三角函数的应用(求线段长)
你还学过哪些求线段长的方法?
哪种方法更简便?
解直角三角形至少已知几个条件?
活动一:小组合作、探究策略
以小组为单位合作交流,探究分别在这五种情况下如何解直角三角形,结果写在学案上。
结论:有斜用弦、无斜用切、宁乘勿除、取原避中
活动二:例题板演,规范书写
帮助老师解决课前提出的实际问题
活动三:变式练习,化斜为直
(2016?西宁) 如图,为保护门源百里油菜花海,由游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为 米. (sin56°≈0.8,tan56°≈1.5)
D
C
A
B
100米
56°
45°
活动四:活动活用、直击中考
(2015锦州)第22题 如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长。
75°
30°
45°
E
F
通过本节课的学习你能从知识内容、解题策略、思想方法等方面谈谈收获吗?
通过本节课的学习你还有哪些疑问?
通过本节课的学习你还想知道什么?
(教师结束语)
数学建模能够帮助学生在数学学习过程中更好的理清思路,有利于快速解决问题。
课前独立回顾整理完成习题
在教师的引导下学生积极思考回答
学生先独立思考后分组进行交流、归纳、尝试多种方法解决问题并体会各种求
解方法之间的差异共性
师生共同分析教师板演
总结实际应用的两个基本图形,体会运用三角函数的简便、直观性。
引导学生独立思考,学会在图中添加适当的辅助线,将非直角问题转化为直角三角形中元素之间的关系。
小结本节课所学的内容,谈学习心得体会。
从实际生活中抽象出数学问题,让学生感受数学建模思想的运用。
1——5习题的设置,目的让学生感知直角三角形中至少已知两个元素(且至少有一边)可求其它元素,即确定直角三角形唯一的条件。
这是本节课的重点,让学生归纳和讨论,理解解直角三角形有几种情况,同时运用了多次分类的思想要让学生深刻体会。
尝试多种方法比较、渗透数形结合的思想
体会转化的数学思想及方程的思想在解题中的应用,提高学生分析问题、解决问题的能力
学会多方法、多角度分析解决问题,体会数学知识环环相扣的联系及统一。
培养学生及时总结,将知识内化、升华。
目
板
书
设
计
课 题
求线段长的方法
作
用
数形结合 分类
解斜三角形 锐角三角函数及应用 解题策略
转化
建
模
A A
D B C B D C
思维导图式板书可以直观形象地展示思维过程,提高课堂教学效率,更有利于培养学生的发散思维和学习能力
教材分析
“锐角三角函数”是《数学课程标准》中“空间与图形”领域的重要内容,初中阶段主要研究锐角三角函数、解直角三角形及运用三角函数解决与直角三角形有关的实际问题,是高中数学三角学的基础,起着承上启下的作用,因此这部分也是中考必考内容之一,在中考复习中必须给予重视,通过学习,学生进一步把形和数结合起来,提高了分析和解决问题的能力,因此,本节课的教学重点为:从实际问题中抽象出基本图形,掌握并灵活应用各种关系解直角三角形。
教学目标
1、掌握并灵活应用各种关系解直角三角形。
2、经历从实际情况中抽象出数学图形和数学符号的过程,感受方程的思想在锐角三角函数中的应用,积累数学建模的经验。
3、以历观察、讨论等数学活动过程,发展合情推理能力,能有条理地、清晰地阐述自己的观点。
4、体验数形之间的联系,注重数学思想的运用,培养学生分析问题解决问题的能力。
学情分析
九年级学生已经牢固掌握了勾股定理,三角形相似,也已经学习过锐角三角函数、特殊角度的三角函数值,在此基础上,解直角三角形难度并不大,但要达到熟练运用的程度还有一定困难,学生抽象概括能力也有,限,综合运用所学知识解决问题,将实际问题抽象为数学问题的能力都有待提高,因此,我认为本节课的教学难点是:从实际问题中抽象出基本图形,掌握并灵活应用各种关系解直角三角形。
教学过程
教学环节
教 师 活 动
学 生 活 动
设 计 意 图
一、
创设情境
二、
课前整理
复习回顾
三、
合用交流
探求新知
四、
发展思维
应用拓展
五、
归纳小结
内化升华
老师有一个问题请同学们帮忙
问题:一中和二中都位于中华路MN上,它们相聚300m,一中、二中及兀术花园构成了一个三角形△ABC测得∠ACB约为30°,∠ABM约为60°,请求出兀术花园到中华MN的距离是多少?
你想用什么知识解决这一问题?
本节课我们就来学习中考专项复习——锐角三角函数及应用
BC=300米
30°
60°
学生回顾锐角三角函数主要知识点完成课前练习
三角函数的应用(求线段长)
你还学过哪些求线段长的方法?
哪种方法更简便?
解直角三角形至少已知几个条件?
活动一:小组合作、探究策略
以小组为单位合作交流,探究分别在这五种情况下如何解直角三角形,结果写在学案上。
结论:有斜用弦、无斜用切、宁乘勿除、取原避中
活动二:例题板演,规范书写
帮助老师解决课前提出的实际问题
活动三:变式练习,化斜为直
(2016?西宁) 如图,为保护门源百里油菜花海,由游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为 米. (sin56°≈0.8,tan56°≈1.5)
D
C
A
B
100米
56°
45°
活动四:活动活用、直击中考
(2015锦州)第22题 如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长。
75°
30°
45°
E
F
通过本节课的学习你能从知识内容、解题策略、思想方法等方面谈谈收获吗?
通过本节课的学习你还有哪些疑问?
通过本节课的学习你还想知道什么?
(教师结束语)
数学建模能够帮助学生在数学学习过程中更好的理清思路,有利于快速解决问题。
课前独立回顾整理完成习题
在教师的引导下学生积极思考回答
学生先独立思考后分组进行交流、归纳、尝试多种方法解决问题并体会各种求
解方法之间的差异共性
师生共同分析教师板演
总结实际应用的两个基本图形,体会运用三角函数的简便、直观性。
引导学生独立思考,学会在图中添加适当的辅助线,将非直角问题转化为直角三角形中元素之间的关系。
小结本节课所学的内容,谈学习心得体会。
从实际生活中抽象出数学问题,让学生感受数学建模思想的运用。
1——5习题的设置,目的让学生感知直角三角形中至少已知两个元素(且至少有一边)可求其它元素,即确定直角三角形唯一的条件。
这是本节课的重点,让学生归纳和讨论,理解解直角三角形有几种情况,同时运用了多次分类的思想要让学生深刻体会。
尝试多种方法比较、渗透数形结合的思想
体会转化的数学思想及方程的思想在解题中的应用,提高学生分析问题、解决问题的能力
学会多方法、多角度分析解决问题,体会数学知识环环相扣的联系及统一。
培养学生及时总结,将知识内化、升华。
目
板
书
设
计
课 题
求线段长的方法
作
用
数形结合 分类
解斜三角形 锐角三角函数及应用 解题策略
转化
建
模
A A
D B C B D C
思维导图式板书可以直观形象地展示思维过程,提高课堂教学效率,更有利于培养学生的发散思维和学习能力
