北师大版九年级数学下册:1.6 利用三角函数测高 教案
文档属性
| 名称 | 北师大版九年级数学下册:1.6 利用三角函数测高 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 370.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 00:00:00 | ||
图片预览

文档简介
利用三角函数测高
【教学目标】
一、知识与技能:
1.能够根据三角函数测高的原理制定测量方案,能够制作测倾器并掌握测倾器测角的方法。
2.能综合应用直角三角形的边角关系的知识解决实际问题。
二、过程与方法:
1.经历制作测倾器的过程,提高学生数学动手能力,并会对仪器进行调整,对测量结果进行矫正,从而使测量结果符合实际。
2.经历策划测量方案的过程,提高数学应用能力和综合分析能力。
三、情感态度与价值观:
能够主动积极地思考,积极地投入到数学活动中去,提高数学学习的兴趣,培养不怕困难的品质,在活动中发展合作意识和科学精神。
【教学重难点】
1.合理制定方案,掌握用三角函数的知识计算出物体的高度。
2.制作测倾器,理解测倾器的构造原理,并对测量结果进行矫正。
【教学过程】
一、试一试,测量倾斜角:
数学课上,我们用直尺测量长度,用量角器测量角度。生活中,我们是如何测量长度和角度的呢?
测量长度可以用皮尺或卷尺,测量倾斜角可以用测倾器。
简单的测倾器由度盘、铅锤和支杆组成。(如图)
皮尺 测倾器
使用测倾器测量倾斜角的步骤如下:
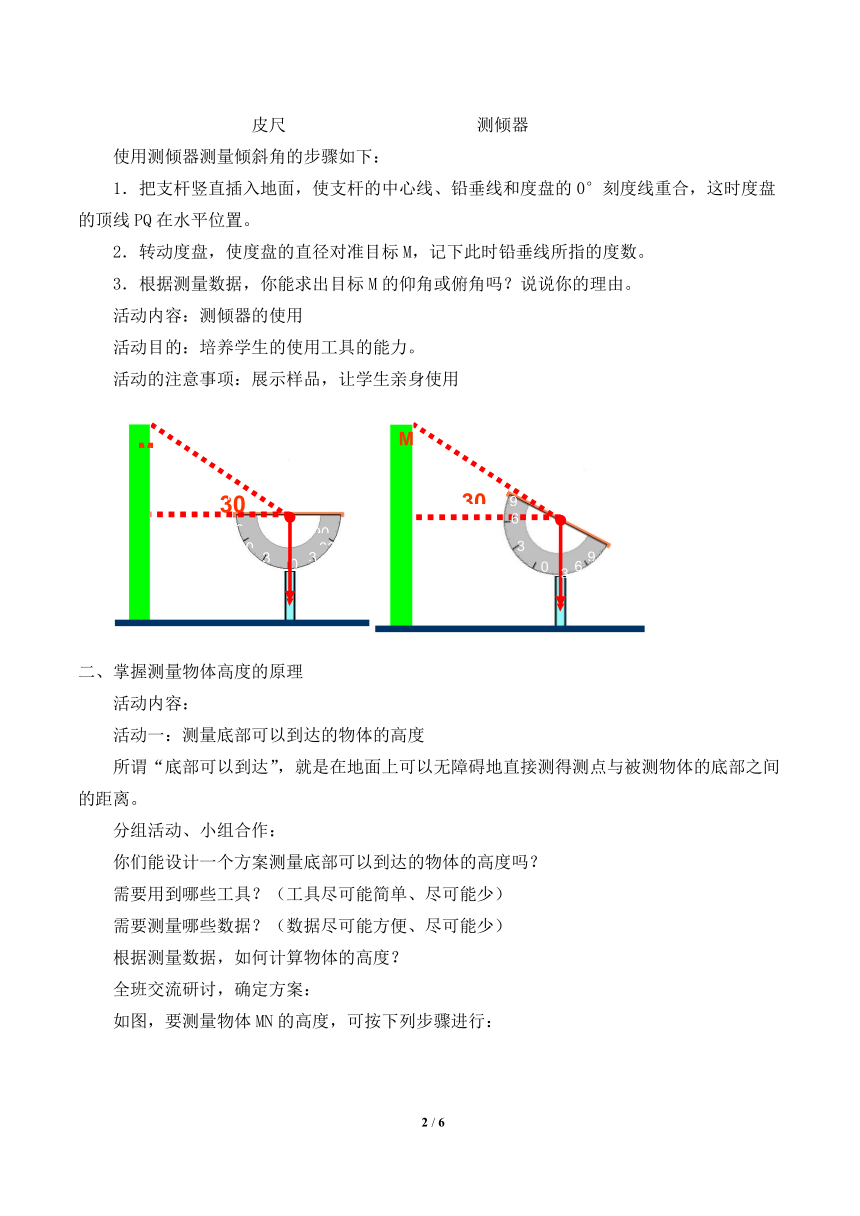
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。
3.根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由。
活动内容:测倾器的使用
活动目的:培养学生的使用工具的能力。
活动的注意事项:展示样品,让学生亲身使用
二、掌握测量物体高度的原理
活动内容:
活动一:测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离。
分组活动、小组合作:
你们能设计一个方案测量底部可以到达的物体的高度吗?
需要用到哪些工具?(工具尽可能简单、尽可能少)
需要测量哪些数据?(数据尽可能方便、尽可能少)
根据测量数据,如何计算物体的高度?
全班交流研讨,确定方案:
如图,要测量物体MN的高度,可按下列步骤进行:
在测点A处安置测倾器,测得物体顶部M的仰角∠MCE=。
量出测点A到物体底部N的水平距离AN=。
量出测倾器的高度AC=(即顶线PQ成水平位置时,它与地面的距离)。
根据测量数据,你能求出物体MN的高度吗?说说你的理由。
解:由题可得:CE=AN=,NE=AC=
在Rt△CEM中,
∴
∴
活动二:测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离。
分组活动、小组合作:
你们能设计一个方案测量底部可以到达的物体的高度吗?
需要用到哪些工具?(工具尽可能简单、尽可能少)
需要测量哪些数据?(数据尽可能方便、尽可能少)
根据测量数据,如何计算物体的高度?
全班交流研讨,确定方案:
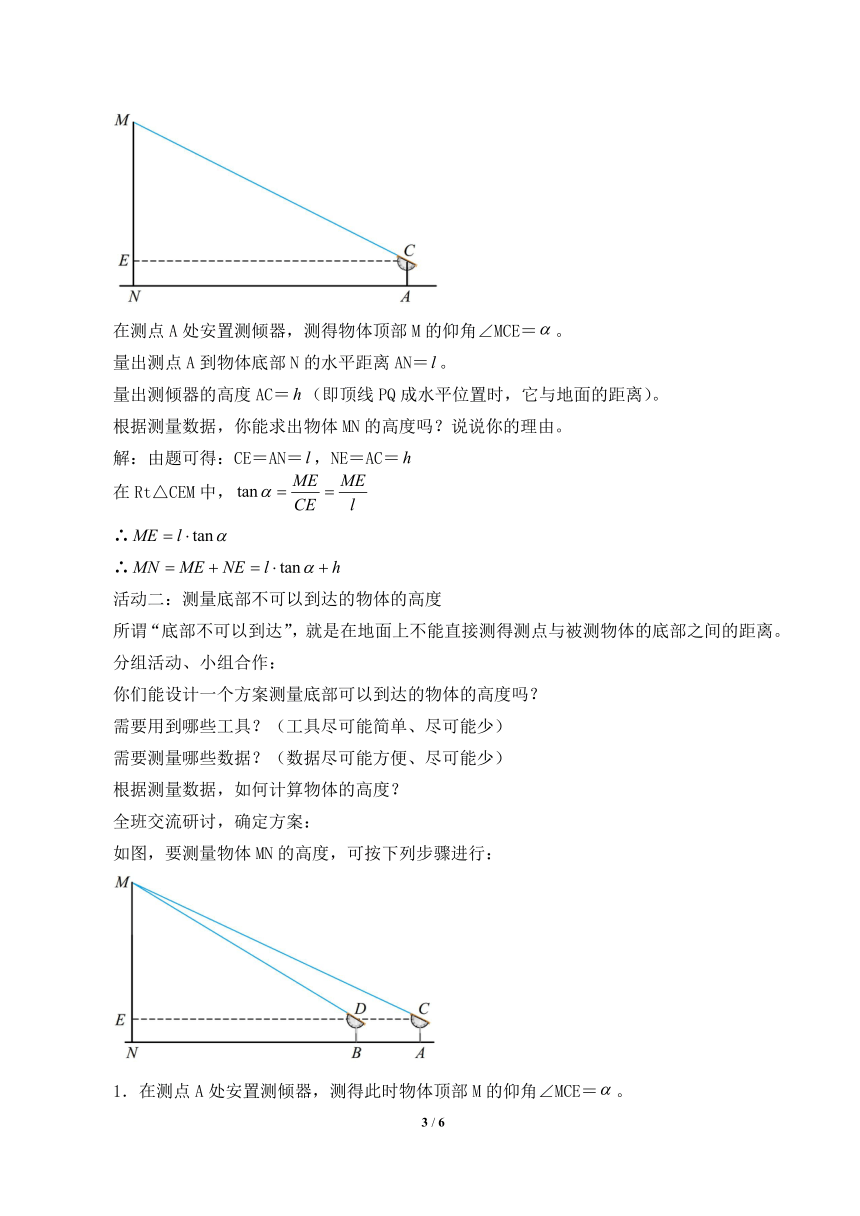
如图,要测量物体MN的高度,可按下列步骤进行:
1.在测点A处安置测倾器,测得此时物体顶部M的仰角∠MCE=。
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时物体顶部M的仰角∠MDE=。
3.量出测倾器的高度AC=BD=,以及测点A,B之间的距离AB=。
根据测量数据,你能求出物体MN的高度吗?说说你的理由。
解:由题可得:AC=BD=NE=,CD=AB=
在Rt△CEM中, ∴
在Rt△DEM中, ∴
由得:
∴
活动目的:让学生熟悉掌握三角函数的公式,对已学知识进行巩固温习,同时提高第二课时利用数据解决问题时的能力。
注意事项:应给学生足够的时间思考,是否还有其他方法测量物体高度,由学生用自己的语言进行归纳总结,加强知识与实际问题的联系。同时发展学生符号化的数学思维习惯。
三、实际应用
活动内容:例题1,如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30?,而当时测倾器离地面1.4m,求学校主楼的高度。(精确到0.1米)
过A作AM⊥CD,在Rt△ADM中,则AB=CM=1.4,
,
即17.3
所以,CD=17.3+1.4=18.7
答:学校主楼的高度是18.7米。
例题2,河对岸的高层建筑AB,为测量其高,在C处由D点用测量仪测得顶端A的仰角为30?,向高层建筑物前进50m到达C?处,由D?测得顶端A的仰角为45?,已知测量仪CD=C?D?=1.2m,求建筑物AB=的高(精确到0.1米)。
延长DD?,交AB于点E。
在Rt△AD?E中,由得,
在Rt△ADE中,由得,
所以50=,则
所以物体高度为AB=68.3+1.2=69.5米
四、实际演练
1. 制作测倾器
活动内容:教师展示测倾器,并讲解测倾器的构造
及其使用原理。1、把支杆竖直接触地面(可借助直角三
角板人手扶稳),使支杆的中心线、铅垂线和度盘的0刻
度线重合,这时度盘的顶线PQ在水平位置。2、转动度盘,
使度盘的直径对准目标M,记下此时铅垂线所指的度数。3、根据“同角的余角相等”,将“读数”与“仰角”(俯角)建立联系。
活动目的:明确操作步骤,理解数据与情境的联系。掌握测倾器操作的方式,合理读取数据,并掌握如何减少误差。
注意事项:(1)目标M要在度盘所在平面内(即目标M在PQ所在直线上);(2)铅垂线要停稳后,观察者在正面进行读数记录;(3)目标M最终高度要加上测倾器本身高度。
2. 制定测量高度的方案
活动内容:(1)活动分组:6人一组,分工合作(组长A、器材管理员B、测量员C、记录员D、计算员E、复核员F)
(2)小组根据需要测量的对象的实际情况,先讨论研究测量方案及具体的操作步骤,分别讨论底部可以到达的物体的高度(操场边的国旗)、底部不可以到达的物体的高度(围墙外的居民楼)各需要测量哪些数据。
活动目的:明确活动任务,根据方案实施测量计划,确保活动能够组织有序,高效完成测量工作。事前预“算”测量数据,为解决实际问题提前热身。
注意事项:提前设计预案,每个成员均要参与设计,清楚自己的分工。给予足够时间让学生经历运算过程,锻炼学生处理数据的能力。
五、课堂小结
(1)到目前为止,你有哪些测量物体高度的方法?
(2)如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离?【作业布置】
活动内容:
1.学生根据教师的讲解及要求,课后完成测倾器制作,小组合作完成。
2.选择一个底部可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等。
3.选择一个底部不可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等。 (下表作参考)
课题 ?
测量示意图 ?
测得数据 测量项目 第一次 第二次 平均值
? ? ? ?
? ? ? ?
? ? ? ?
计算过程 ?
活动感受 ?
负责人及参加人员 ?
计算者和复核者 ?
指导教师审核意见 ?
备注 ?
注意事项:教师讲解仪器制作的方法及要素,确保测倾器误差小。学生作品完成后,教师应进行检查验收,确保收集数据有效。
5 / 6
【教学目标】
一、知识与技能:
1.能够根据三角函数测高的原理制定测量方案,能够制作测倾器并掌握测倾器测角的方法。
2.能综合应用直角三角形的边角关系的知识解决实际问题。
二、过程与方法:
1.经历制作测倾器的过程,提高学生数学动手能力,并会对仪器进行调整,对测量结果进行矫正,从而使测量结果符合实际。
2.经历策划测量方案的过程,提高数学应用能力和综合分析能力。
三、情感态度与价值观:
能够主动积极地思考,积极地投入到数学活动中去,提高数学学习的兴趣,培养不怕困难的品质,在活动中发展合作意识和科学精神。
【教学重难点】
1.合理制定方案,掌握用三角函数的知识计算出物体的高度。
2.制作测倾器,理解测倾器的构造原理,并对测量结果进行矫正。
【教学过程】
一、试一试,测量倾斜角:
数学课上,我们用直尺测量长度,用量角器测量角度。生活中,我们是如何测量长度和角度的呢?
测量长度可以用皮尺或卷尺,测量倾斜角可以用测倾器。
简单的测倾器由度盘、铅锤和支杆组成。(如图)
皮尺 测倾器
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。
3.根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由。
活动内容:测倾器的使用
活动目的:培养学生的使用工具的能力。
活动的注意事项:展示样品,让学生亲身使用
二、掌握测量物体高度的原理
活动内容:
活动一:测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离。
分组活动、小组合作:
你们能设计一个方案测量底部可以到达的物体的高度吗?
需要用到哪些工具?(工具尽可能简单、尽可能少)
需要测量哪些数据?(数据尽可能方便、尽可能少)
根据测量数据,如何计算物体的高度?
全班交流研讨,确定方案:
如图,要测量物体MN的高度,可按下列步骤进行:
在测点A处安置测倾器,测得物体顶部M的仰角∠MCE=。
量出测点A到物体底部N的水平距离AN=。
量出测倾器的高度AC=(即顶线PQ成水平位置时,它与地面的距离)。
根据测量数据,你能求出物体MN的高度吗?说说你的理由。
解:由题可得:CE=AN=,NE=AC=
在Rt△CEM中,
∴
∴
活动二:测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离。
分组活动、小组合作:
你们能设计一个方案测量底部可以到达的物体的高度吗?
需要用到哪些工具?(工具尽可能简单、尽可能少)
需要测量哪些数据?(数据尽可能方便、尽可能少)
根据测量数据,如何计算物体的高度?
全班交流研讨,确定方案:
如图,要测量物体MN的高度,可按下列步骤进行:
1.在测点A处安置测倾器,测得此时物体顶部M的仰角∠MCE=。
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时物体顶部M的仰角∠MDE=。
3.量出测倾器的高度AC=BD=,以及测点A,B之间的距离AB=。
根据测量数据,你能求出物体MN的高度吗?说说你的理由。
解:由题可得:AC=BD=NE=,CD=AB=
在Rt△CEM中, ∴
在Rt△DEM中, ∴
由得:
∴
活动目的:让学生熟悉掌握三角函数的公式,对已学知识进行巩固温习,同时提高第二课时利用数据解决问题时的能力。
注意事项:应给学生足够的时间思考,是否还有其他方法测量物体高度,由学生用自己的语言进行归纳总结,加强知识与实际问题的联系。同时发展学生符号化的数学思维习惯。
三、实际应用
活动内容:例题1,如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30?,而当时测倾器离地面1.4m,求学校主楼的高度。(精确到0.1米)
过A作AM⊥CD,在Rt△ADM中,则AB=CM=1.4,
,
即17.3
所以,CD=17.3+1.4=18.7
答:学校主楼的高度是18.7米。
例题2,河对岸的高层建筑AB,为测量其高,在C处由D点用测量仪测得顶端A的仰角为30?,向高层建筑物前进50m到达C?处,由D?测得顶端A的仰角为45?,已知测量仪CD=C?D?=1.2m,求建筑物AB=的高(精确到0.1米)。
延长DD?,交AB于点E。
在Rt△AD?E中,由得,
在Rt△ADE中,由得,
所以50=,则
所以物体高度为AB=68.3+1.2=69.5米
四、实际演练
1. 制作测倾器
活动内容:教师展示测倾器,并讲解测倾器的构造
及其使用原理。1、把支杆竖直接触地面(可借助直角三
角板人手扶稳),使支杆的中心线、铅垂线和度盘的0刻
度线重合,这时度盘的顶线PQ在水平位置。2、转动度盘,
使度盘的直径对准目标M,记下此时铅垂线所指的度数。3、根据“同角的余角相等”,将“读数”与“仰角”(俯角)建立联系。
活动目的:明确操作步骤,理解数据与情境的联系。掌握测倾器操作的方式,合理读取数据,并掌握如何减少误差。
注意事项:(1)目标M要在度盘所在平面内(即目标M在PQ所在直线上);(2)铅垂线要停稳后,观察者在正面进行读数记录;(3)目标M最终高度要加上测倾器本身高度。
2. 制定测量高度的方案
活动内容:(1)活动分组:6人一组,分工合作(组长A、器材管理员B、测量员C、记录员D、计算员E、复核员F)
(2)小组根据需要测量的对象的实际情况,先讨论研究测量方案及具体的操作步骤,分别讨论底部可以到达的物体的高度(操场边的国旗)、底部不可以到达的物体的高度(围墙外的居民楼)各需要测量哪些数据。
活动目的:明确活动任务,根据方案实施测量计划,确保活动能够组织有序,高效完成测量工作。事前预“算”测量数据,为解决实际问题提前热身。
注意事项:提前设计预案,每个成员均要参与设计,清楚自己的分工。给予足够时间让学生经历运算过程,锻炼学生处理数据的能力。
五、课堂小结
(1)到目前为止,你有哪些测量物体高度的方法?
(2)如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离?【作业布置】
活动内容:
1.学生根据教师的讲解及要求,课后完成测倾器制作,小组合作完成。
2.选择一个底部可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等。
3.选择一个底部不可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等。 (下表作参考)
课题 ?
测量示意图 ?
测得数据 测量项目 第一次 第二次 平均值
? ? ? ?
? ? ? ?
? ? ? ?
计算过程 ?
活动感受 ?
负责人及参加人员 ?
计算者和复核者 ?
指导教师审核意见 ?
备注 ?
注意事项:教师讲解仪器制作的方法及要素,确保测倾器误差小。学生作品完成后,教师应进行检查验收,确保收集数据有效。
5 / 6
