北师大版九年级数学下册:1.6利用三角函数测高 教案
文档属性
| 名称 | 北师大版九年级数学下册:1.6利用三角函数测高 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 17:56:09 | ||
图片预览



文档简介
课题:1.6利用三角函数测高 课型:新授课 年级:九年级
教学目标:
1.经历设计活动方案、自制仪器或运用仪器进行实地测量以及撰写活动报告的过程.
2.能够对所得到的数据进行分析,能够对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果.
3.能够设计方案测量物体的高度,综合运用直角三角形边角关系的知识解决实际问题,提高解决问题的能力.
4.体会数形之间的联系,逐步学会利用数形结合的思想分析问题、解决问题.
教学重点与难点:
重点:经历设计活动方案、自制仪器或运用仪器进行实地测量以及撰写活动报告的过程..
难点:设计活动方案、自制仪器,综合运用直角三角形边角关系的知识解决实际问题.
课前准备:自制测倾器(或经纬仪、测角仪等)、皮尺等测量工具,多媒体课件.
教学过程:
一、创设情境,导入新课
活动内容:回答下列问题.
问题1:在现实生活中需要测量像旗杆、高楼、塔等较高且顶部不可到达的物体的高度,根据我们所学的知识,同学们有哪些测量方案?
问题2:这些测量的方法都用到了什么知识?
问题3:如何利用直角三角形的边角关系,测量底部不可以直接到达的物体的高度呢?
处理方式:问题1、2先让学生思考、讨论交流,然后再回答,对于问题1可能有以下结果:
(1)利用太阳光下的影子测量;
(2)利用标杆测量;
(3)利用镜子的反射测量.
…………
对于问题2学生回答:“三角形相似,根据相似比求其高度”.对于问题3学生一脸迷茫,充满疑惑。教师及时引导:看来这个问题暂时有点儿难,今天让我们一起去探究学习如何利用三角函数测高.(板书:1.6 利用三角函数测高),学完本节内容相信大家就能轻松解决上面的问题了.
设计意图:通过创设情境,既复习巩固了三角形相似的内容,又极大地激发了学生学习兴趣,为下面的学习作铺垫,效果非常好.
二、动手实践、感悟新知
今天我们活动的课题:利用直角三角形的边角关系测量物体的高度.
活动方式:分组活动或全班交流研讨.
活动工具:测倾器(或测角仪等),皮尺等测量工具.
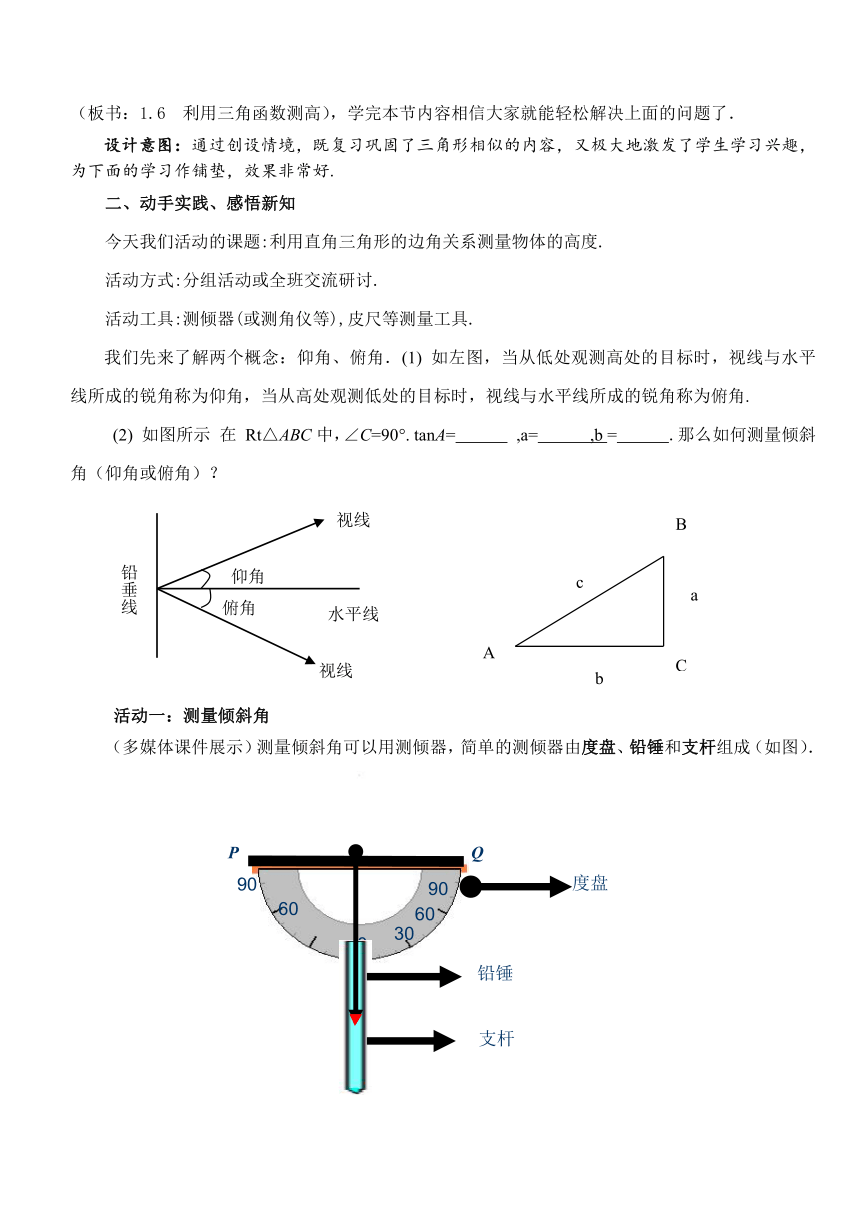
我们先来了解两个概念:仰角、俯角.(1) 如左图,当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角,当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角.
(2) 如图所示 在 Rt△ABC中,∠C=90°. tanA= ,a= ,b = .那么如何测量倾斜角(仰角或俯角)?
活动一:测量倾斜角
(多媒体课件展示)测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线,铅垂线和度盘的0刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
根据刚才测量数据,你能求出目标M的仰角或俯角吗?说说你的理由(学生分组讨论后回答).
∵∠3=30°,∠3+∠2=90°,
∠1+∠2=90°
∴∠1=∠3=30°
∴目标M的仰角为30°(依据是同角的余角相等).
也就是说,测倾器上铅垂线所示的度数就是物体仰角的度数.
下面我们来看看怎样利用测倾器测量物体的高度.
设计意图:通过演示如何使用测倾器并讲解注意事项,培养学生的使用工具的能力.
活动二:测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.如图,要测量物体MN的高度,可按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器(即测角仪)的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
解:在Rt△MEC中,因为tanα=,所以ME=tana·EC=l·tanα.
所以MN=ME+EN=l·tanα+a.
例1 (多媒体课件展示)
同学们能利用自角三角形的边角关系用测角仪和皮尺测出底部可以到达的物体的高度.但现实生活中,还存在有底部不可以到达的物体.它们的高度如何测量呢?
设计意图:让学生先“热热身”进行简单的测量,初步掌握测量的步骤并推导出一般性的公式,为测量底部不可以直接到达的物体的高度做好铺垫.
活动三:测量底部不可以直接到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体底部之间的距离.
如图,要测量物体MN的高度,使用侧倾器测一次仰角够吗?(学生回答:要测量物体MN的高度,测一次仰角是不够的).还需哪些条件,测量哪些数据?(学生在各小组内讨论后回答)
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾(A,B与N在一条直线上),测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
提问:根据测量数据,你能求出物体MN的高度吗?说说你的理由.
学生根据测量数据,写出计算物体MN的高度过程:
解:∵在Rt△MDE中,ED=ME/tanβ
在Rt△MCE中,EC =ME/tanα
∴EC-ED=b
∴
∴
∴
设计意图:这个活动的设计方案对于学生来说有一定的难度,所以,在教学中要给学生留有充分的讨论时间,不可急于求成,也可各组间穿插讨论;同时教师要深入小组内讨论,帮助有困难的小组.这个活动的设计方案不唯一,学生说的只要在理,就应该肯定和鼓励.教师还要关注学生是否积极参与,是否真正理解. 进一步培养学生运用所学,解决实际应用问题的意识.
议一议:
1.到目前为止,你有哪些测量物体高度的方法?
2.如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离?
学生先独立思考、讨论交流,然后再回答,对于问题1可能有以下结果:
(1)利用三角函数的知识可以测量物体的高度.
(2)利用三角形相似的知识也可以.
(3)还有利用全等三角形的知识也可以测量物体的高度.
对于问题2可以利用今天所学的三角函数知识解决.教师对学生的回答予以鼓励和肯定.
设计意图:通过及时总结测量物体高度的方法,培养学生的概括归纳能力.
三、联系实际、应用新知
例2:(多媒体课件展示)
1.请根据小明测得的数据,填表中的空格.
2. 已知测倾器的高CE=DF=1m,通过计算求得该大厦的高为______米 (精确到1米).
解:1. 30° 45° 60m
2. 在Rt△AEG中,EG=AG/tan30°=1.732AG.
在Rt△AFG中,FG=AG/tan45°=AG,
EG - FG =CD,
1.732AG-AG=60,
AG=60÷0.732≈81.96(m) .
AB=AG+1≈83(m) .
注意事项:在测量当中误差的处理办法.
设计意图:通过两道例题的讲解,进一步培养了学生运用数形结合思想分析和解决问题的能力,帮助学生树立学好数学的信心.
四、达标检测,反馈提高
通过本节课的学习,同学们的收获真多!收获的质量如何呢?请完成导学案中的达标检测题.(同时多媒体出示)
A组:
1.如图1-16,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
2.如图1-17,小明想测量电线杆AB的高度,发现电线杆的影子恰好落在地面BC和斜坡的坡面CD上,测得BC = 10米,CD = 4米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为 米.
3.如图1-18,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.1米)( );
A. 1 366.0米 B. 1 482.1米 C. 1 295.9米 D. 1 508.2米
4.如图1-19,两建筑物的水平距离为a米,从A点测得D点的俯角为α,测得C点的俯角为β. 则较低建筑物CD的高度为( ).
A.a米 B. C. D. a (tanβ- tanα)
B组:
5.如图,为庆祝元旦节日,阴平中学在主楼的顶部D和大门的上方A之间挂一些彩旗.经测量,得到大门AB的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求:学校主楼的高度(精确到0.01m).
处理方式:学生做完后,教师出示答案,指导学生校对,并统计学生答题情况.学生根据答案进行纠错.
设计意图:学以致用,当堂检测及时获知学生对所学知识掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高,明确哪些学生需要在课后加强辅导,达到全面提高的目的.
五、回顾反思,提炼升华
同学们,竹子每生长一步,必做小结,所以它是世界上长的最快的植物,数学的学习也是如此.通过这节课的学习,你有哪些收获?有何感想?学会了哪些方法?先想一想,再分享给大家.
学生畅谈自己的收获!
设计意图:通过小结,,使学生对本节课所学进行梳理,养成反思与总结的习惯,培养自我反馈,自主发展的意识.对个别学困生来说是进一步强调和落实,最终力争让每位学生都能达到本节课的活动目标
六、布置作业,课堂延伸
必做题:1.完成本节数学助学P199第8题 第9题.
选做题:习题1.7 问题解决 第1题 第2题 第3题.
设计意图:旨在帮助学生巩固所学知识,题目间有层次的递进.
板书设计:
§1.6利用三角函数测高
活动一:测量倾斜角 活动二:测量底部可以到达的物体的高度
活动三:测量底部不可以到达的物体的高度
例1
解:
例2
解: 投
影
区
学 生 活 动 区
教学目标:
1.经历设计活动方案、自制仪器或运用仪器进行实地测量以及撰写活动报告的过程.
2.能够对所得到的数据进行分析,能够对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果.
3.能够设计方案测量物体的高度,综合运用直角三角形边角关系的知识解决实际问题,提高解决问题的能力.
4.体会数形之间的联系,逐步学会利用数形结合的思想分析问题、解决问题.
教学重点与难点:
重点:经历设计活动方案、自制仪器或运用仪器进行实地测量以及撰写活动报告的过程..
难点:设计活动方案、自制仪器,综合运用直角三角形边角关系的知识解决实际问题.
课前准备:自制测倾器(或经纬仪、测角仪等)、皮尺等测量工具,多媒体课件.
教学过程:
一、创设情境,导入新课
活动内容:回答下列问题.
问题1:在现实生活中需要测量像旗杆、高楼、塔等较高且顶部不可到达的物体的高度,根据我们所学的知识,同学们有哪些测量方案?
问题2:这些测量的方法都用到了什么知识?
问题3:如何利用直角三角形的边角关系,测量底部不可以直接到达的物体的高度呢?
处理方式:问题1、2先让学生思考、讨论交流,然后再回答,对于问题1可能有以下结果:
(1)利用太阳光下的影子测量;
(2)利用标杆测量;
(3)利用镜子的反射测量.
…………
对于问题2学生回答:“三角形相似,根据相似比求其高度”.对于问题3学生一脸迷茫,充满疑惑。教师及时引导:看来这个问题暂时有点儿难,今天让我们一起去探究学习如何利用三角函数测高.(板书:1.6 利用三角函数测高),学完本节内容相信大家就能轻松解决上面的问题了.
设计意图:通过创设情境,既复习巩固了三角形相似的内容,又极大地激发了学生学习兴趣,为下面的学习作铺垫,效果非常好.
二、动手实践、感悟新知
今天我们活动的课题:利用直角三角形的边角关系测量物体的高度.
活动方式:分组活动或全班交流研讨.
活动工具:测倾器(或测角仪等),皮尺等测量工具.
我们先来了解两个概念:仰角、俯角.(1) 如左图,当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角,当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角.
(2) 如图所示 在 Rt△ABC中,∠C=90°. tanA= ,a= ,b = .那么如何测量倾斜角(仰角或俯角)?
活动一:测量倾斜角
(多媒体课件展示)测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线,铅垂线和度盘的0刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
根据刚才测量数据,你能求出目标M的仰角或俯角吗?说说你的理由(学生分组讨论后回答).
∵∠3=30°,∠3+∠2=90°,
∠1+∠2=90°
∴∠1=∠3=30°
∴目标M的仰角为30°(依据是同角的余角相等).
也就是说,测倾器上铅垂线所示的度数就是物体仰角的度数.
下面我们来看看怎样利用测倾器测量物体的高度.
设计意图:通过演示如何使用测倾器并讲解注意事项,培养学生的使用工具的能力.
活动二:测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.如图,要测量物体MN的高度,可按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器(即测角仪)的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
解:在Rt△MEC中,因为tanα=,所以ME=tana·EC=l·tanα.
所以MN=ME+EN=l·tanα+a.
例1 (多媒体课件展示)
同学们能利用自角三角形的边角关系用测角仪和皮尺测出底部可以到达的物体的高度.但现实生活中,还存在有底部不可以到达的物体.它们的高度如何测量呢?
设计意图:让学生先“热热身”进行简单的测量,初步掌握测量的步骤并推导出一般性的公式,为测量底部不可以直接到达的物体的高度做好铺垫.
活动三:测量底部不可以直接到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体底部之间的距离.
如图,要测量物体MN的高度,使用侧倾器测一次仰角够吗?(学生回答:要测量物体MN的高度,测一次仰角是不够的).还需哪些条件,测量哪些数据?(学生在各小组内讨论后回答)
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾(A,B与N在一条直线上),测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
提问:根据测量数据,你能求出物体MN的高度吗?说说你的理由.
学生根据测量数据,写出计算物体MN的高度过程:
解:∵在Rt△MDE中,ED=ME/tanβ
在Rt△MCE中,EC =ME/tanα
∴EC-ED=b
∴
∴
∴
设计意图:这个活动的设计方案对于学生来说有一定的难度,所以,在教学中要给学生留有充分的讨论时间,不可急于求成,也可各组间穿插讨论;同时教师要深入小组内讨论,帮助有困难的小组.这个活动的设计方案不唯一,学生说的只要在理,就应该肯定和鼓励.教师还要关注学生是否积极参与,是否真正理解. 进一步培养学生运用所学,解决实际应用问题的意识.
议一议:
1.到目前为止,你有哪些测量物体高度的方法?
2.如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离?
学生先独立思考、讨论交流,然后再回答,对于问题1可能有以下结果:
(1)利用三角函数的知识可以测量物体的高度.
(2)利用三角形相似的知识也可以.
(3)还有利用全等三角形的知识也可以测量物体的高度.
对于问题2可以利用今天所学的三角函数知识解决.教师对学生的回答予以鼓励和肯定.
设计意图:通过及时总结测量物体高度的方法,培养学生的概括归纳能力.
三、联系实际、应用新知
例2:(多媒体课件展示)
1.请根据小明测得的数据,填表中的空格.
2. 已知测倾器的高CE=DF=1m,通过计算求得该大厦的高为______米 (精确到1米).
解:1. 30° 45° 60m
2. 在Rt△AEG中,EG=AG/tan30°=1.732AG.
在Rt△AFG中,FG=AG/tan45°=AG,
EG - FG =CD,
1.732AG-AG=60,
AG=60÷0.732≈81.96(m) .
AB=AG+1≈83(m) .
注意事项:在测量当中误差的处理办法.
设计意图:通过两道例题的讲解,进一步培养了学生运用数形结合思想分析和解决问题的能力,帮助学生树立学好数学的信心.
四、达标检测,反馈提高
通过本节课的学习,同学们的收获真多!收获的质量如何呢?请完成导学案中的达标检测题.(同时多媒体出示)
A组:
1.如图1-16,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
2.如图1-17,小明想测量电线杆AB的高度,发现电线杆的影子恰好落在地面BC和斜坡的坡面CD上,测得BC = 10米,CD = 4米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为 米.
3.如图1-18,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.1米)( );
A. 1 366.0米 B. 1 482.1米 C. 1 295.9米 D. 1 508.2米
4.如图1-19,两建筑物的水平距离为a米,从A点测得D点的俯角为α,测得C点的俯角为β. 则较低建筑物CD的高度为( ).
A.a米 B. C. D. a (tanβ- tanα)
B组:
5.如图,为庆祝元旦节日,阴平中学在主楼的顶部D和大门的上方A之间挂一些彩旗.经测量,得到大门AB的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求:学校主楼的高度(精确到0.01m).
处理方式:学生做完后,教师出示答案,指导学生校对,并统计学生答题情况.学生根据答案进行纠错.
设计意图:学以致用,当堂检测及时获知学生对所学知识掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高,明确哪些学生需要在课后加强辅导,达到全面提高的目的.
五、回顾反思,提炼升华
同学们,竹子每生长一步,必做小结,所以它是世界上长的最快的植物,数学的学习也是如此.通过这节课的学习,你有哪些收获?有何感想?学会了哪些方法?先想一想,再分享给大家.
学生畅谈自己的收获!
设计意图:通过小结,,使学生对本节课所学进行梳理,养成反思与总结的习惯,培养自我反馈,自主发展的意识.对个别学困生来说是进一步强调和落实,最终力争让每位学生都能达到本节课的活动目标
六、布置作业,课堂延伸
必做题:1.完成本节数学助学P199第8题 第9题.
选做题:习题1.7 问题解决 第1题 第2题 第3题.
设计意图:旨在帮助学生巩固所学知识,题目间有层次的递进.
板书设计:
§1.6利用三角函数测高
活动一:测量倾斜角 活动二:测量底部可以到达的物体的高度
活动三:测量底部不可以到达的物体的高度
例1
解:
例2
解: 投
影
区
学 生 活 动 区
