北师大版九年级数学下册:1.2 30°,45°,60°角的三角函数值 教案
文档属性
| 名称 | 北师大版九年级数学下册:1.2 30°,45°,60°角的三角函数值 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 86.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 17:56:09 | ||
图片预览

文档简介
2 30°,45°,60°角的三角函数值
教学目标
1.经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义.
2.能够进行30°,45°,60°角的三角函数值的计算.
3.能够根据30°,45°,60°的三角函数值说明相应的锐角的大小.
教学重难点
重点
能够进行30°,45°,60°角的三角函数值的计算;能够根据30°,45°,60°角的三角函数值说出相应的锐角大小.
难点
通过探索特殊三角函数值的过程,培养学生进行有关推理的能力.
教学设计
一、复习导入
1.在Rt△ABC中,∠C =90°.
(1)a,b,c三者之间的关系是什么?∠ A+∠ B等于多少度?
(2)如何表示sin A,cos A,tan A,sin B,cos B,tan B?
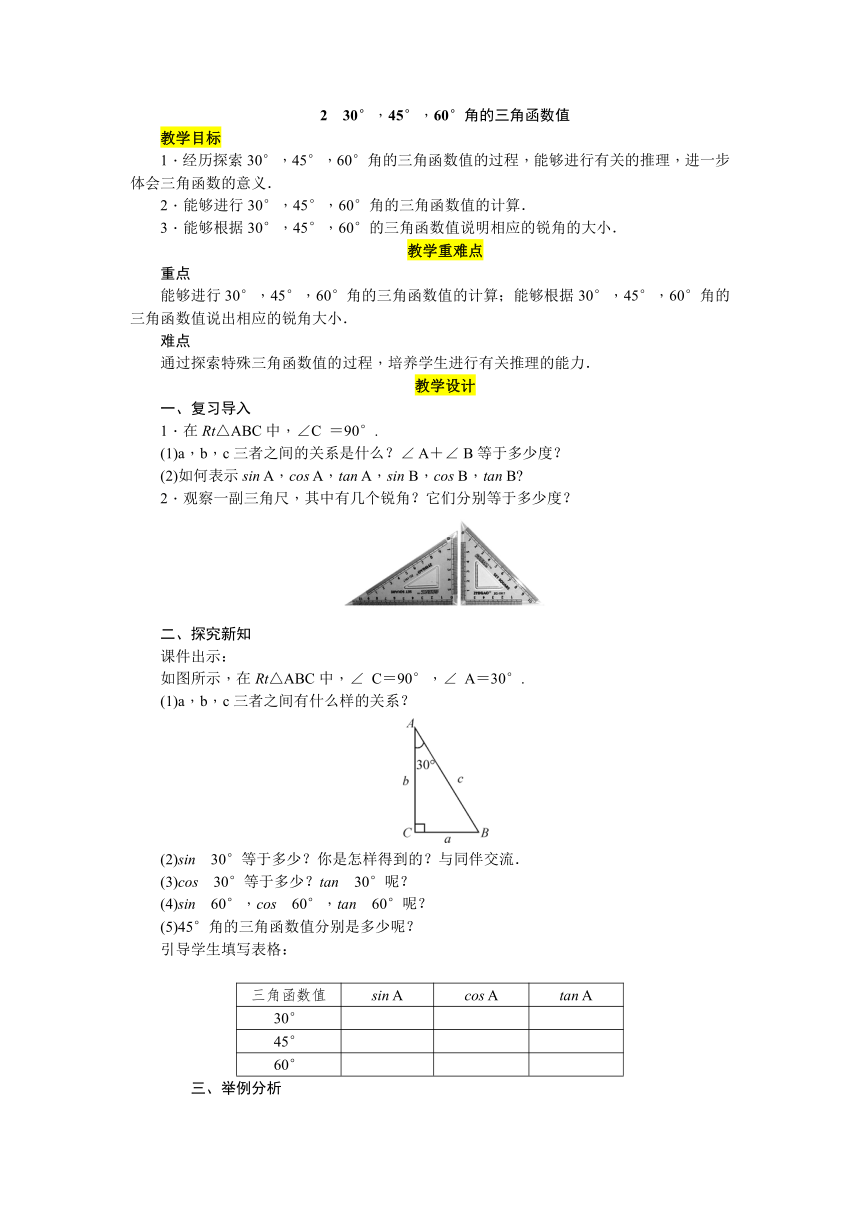
2.观察一副三角尺,其中有几个锐角?它们分别等于多少度?
二、探究新知
课件出示:
如图所示,在Rt△ABC中,∠ C=90°,∠ A=30°.
(1)a,b,c三者之间有什么样的关系?
(2)sin 30°等于多少?你是怎样得到的?与同伴交流.
(3)cos 30°等于多少?tan 30°呢?
(4)sin 60°,cos 60°,tan 60°呢?
(5)45°角的三角函数值分别是多少呢?
引导学生填写表格:
三角函数值
sin A
cos A
tan A
30°
45°
60°
三、举例分析
例1 计算:
(1) sin 30°+cos 45°;
(2) sin 260°+cos 260°-tan 45°.
处理方式:通过记忆特殊角的三角函数值求解,注意格式和过程.
例2 (课件出示教材第9页例2)
引导学生思考如下问题:
(1)你能根据题意画出图形吗?
(2)你能根据所画图形构造直角三角形吗?
(3)你能找到图形中的特殊角吗?
(4)你能根据特殊角的三角函数值求出正确的结果吗?
四、练习巩固
1.下列式子中成立的是 ( )
A.cos 72°<sin 35°<tan 46°
B.sin 35°<tan 46°<cos 72°
C.tan 46°<cos 72°<sin 35°
D.tan 46°<cos 40°<sin 35°
2.已知等腰△ABC的腰长为4 ,底角为30°,则底边上的高为________,周长为________.
3.若(tan A-3)2+=0,则△ABC按角分类是什么三角形?
五、课堂小结
1.易错点:
(1)能进行含30°,45°,60°角的三角函数值的计算;
(2)能根据30°,45°,60°角的三角函数值,说出相应锐角的大小.
2.归纳小结:
sin 30°=,sin 45°=,sin 60°=;
cos 30°=,cos 45°=,cos 60°=;
tan 30°= ,tan 45°=1,tan 60°=.
3.方法规律:
在Rt△ABC中,若∠A+∠B=90°,则有:
sin A=cos (90°-A);
cos A= sin (90°-A) ;
sin B=cos (90°-B);
cos B=sin (90°-B).
六、课外作业
1.教材第9页“随堂练习”第1、2题.
2.教材第10页习题1.3第1~4题.
教学反思
本节课课程设计中引入非常直接,由三角板引入,直击课题,同时也对前两节学习的知识进行了整体的复习,效果很好.设计开门见山,节省了时间,为后面的教学提供了方便.在讲解特殊角的三角函数值时也很详细,可以说前部分的教学很成功,学生理解得很好.
教学目标
1.经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义.
2.能够进行30°,45°,60°角的三角函数值的计算.
3.能够根据30°,45°,60°的三角函数值说明相应的锐角的大小.
教学重难点
重点
能够进行30°,45°,60°角的三角函数值的计算;能够根据30°,45°,60°角的三角函数值说出相应的锐角大小.
难点
通过探索特殊三角函数值的过程,培养学生进行有关推理的能力.
教学设计
一、复习导入
1.在Rt△ABC中,∠C =90°.
(1)a,b,c三者之间的关系是什么?∠ A+∠ B等于多少度?
(2)如何表示sin A,cos A,tan A,sin B,cos B,tan B?
2.观察一副三角尺,其中有几个锐角?它们分别等于多少度?
二、探究新知
课件出示:
如图所示,在Rt△ABC中,∠ C=90°,∠ A=30°.
(1)a,b,c三者之间有什么样的关系?
(2)sin 30°等于多少?你是怎样得到的?与同伴交流.
(3)cos 30°等于多少?tan 30°呢?
(4)sin 60°,cos 60°,tan 60°呢?
(5)45°角的三角函数值分别是多少呢?
引导学生填写表格:
三角函数值
sin A
cos A
tan A
30°
45°
60°
三、举例分析
例1 计算:
(1) sin 30°+cos 45°;
(2) sin 260°+cos 260°-tan 45°.
处理方式:通过记忆特殊角的三角函数值求解,注意格式和过程.
例2 (课件出示教材第9页例2)
引导学生思考如下问题:
(1)你能根据题意画出图形吗?
(2)你能根据所画图形构造直角三角形吗?
(3)你能找到图形中的特殊角吗?
(4)你能根据特殊角的三角函数值求出正确的结果吗?
四、练习巩固
1.下列式子中成立的是 ( )
A.cos 72°<sin 35°<tan 46°
B.sin 35°<tan 46°<cos 72°
C.tan 46°<cos 72°<sin 35°
D.tan 46°<cos 40°<sin 35°
2.已知等腰△ABC的腰长为4 ,底角为30°,则底边上的高为________,周长为________.
3.若(tan A-3)2+=0,则△ABC按角分类是什么三角形?
五、课堂小结
1.易错点:
(1)能进行含30°,45°,60°角的三角函数值的计算;
(2)能根据30°,45°,60°角的三角函数值,说出相应锐角的大小.
2.归纳小结:
sin 30°=,sin 45°=,sin 60°=;
cos 30°=,cos 45°=,cos 60°=;
tan 30°= ,tan 45°=1,tan 60°=.
3.方法规律:
在Rt△ABC中,若∠A+∠B=90°,则有:
sin A=cos (90°-A);
cos A= sin (90°-A) ;
sin B=cos (90°-B);
cos B=sin (90°-B).
六、课外作业
1.教材第9页“随堂练习”第1、2题.
2.教材第10页习题1.3第1~4题.
教学反思
本节课课程设计中引入非常直接,由三角板引入,直击课题,同时也对前两节学习的知识进行了整体的复习,效果很好.设计开门见山,节省了时间,为后面的教学提供了方便.在讲解特殊角的三角函数值时也很详细,可以说前部分的教学很成功,学生理解得很好.
