2020-2021学年数学北师大七年级下册第四章 三角形综合测评试卷(word版含答案)
文档属性
| 名称 | 2020-2021学年数学北师大七年级下册第四章 三角形综合测评试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 168.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 00:00:00 | ||
图片预览

文档简介
第四章
三角形综合测评
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.以下列各组线段为边,能组成三角形的是( )
A.2
cm,5
cm,8
cm
B.3
cm,3
cm,6
cm
C.3
cm,4
cm,5
cm
D.1
cm,2
cm,3
cm
2.下列四个图形中,△ABC的边AB上的高线画法正确的是( )
A
B
C
D
3.如图1,在△ABC中,∠B=55°,∠C=63°,DE∥AB,则∠DEC的度数为( )
A.63°
B.113°
C.55°
D.62°
图1
图2
图3
图4
如图2,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是( A )
A.9
B.14
C.16
D.不能确定
5.如图3,已知MB=ND,∠MBA=∠NDC,添加下列一个条件后仍不能判定△ABM≌△CDN的是( )
A.∠M=∠N
B.AB=CD
C.AM=CN
D.AM∥CN
6.要测量圆形工件的外径,工人师傅设计了如图4所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则这个工件的外径必是CD的长,其依据的是三角形全等的判定条件( )
A.ASA
B.AAS
C.SAS
D.SSS
7.如图5,△ABC≌△ADE,若∠B=70°,∠C=30°,∠DAC=25°,则∠EAC的度数为( )
A.70°
B.80°
C.55°
D.45°
图5
图6
图7
图8
8.如图6,已知OA=OB,OC=OD,若∠O=50°,∠D=35°,则∠OBC的度数为( )
A.95°
B.120°
C.50°
D.105°
9.如图7,在△ABC中,∠B=∠C=65°,BD=CE,BE=CF,则∠DEF的度数是( C )
A.75°
B.70°
C.65°
D.60°
10.如图8,∠BAC=∠ACD=90°,∠ABC=∠D,CE⊥AD,且BE平分∠ABC,有下列结论:①AD=CB;②∠ACE=∠ABC;③AB=CD;④∠CEF=∠CFE.其中正确的是( )
A.仅①③
B.仅①③④
C.仅①②③
D.①②③④
二、填空题(本大题共6小题,每小题3分,共18分)
11.桥梁拉杆、电视塔底座都是三角形结构,这是利用了三角形的
性.
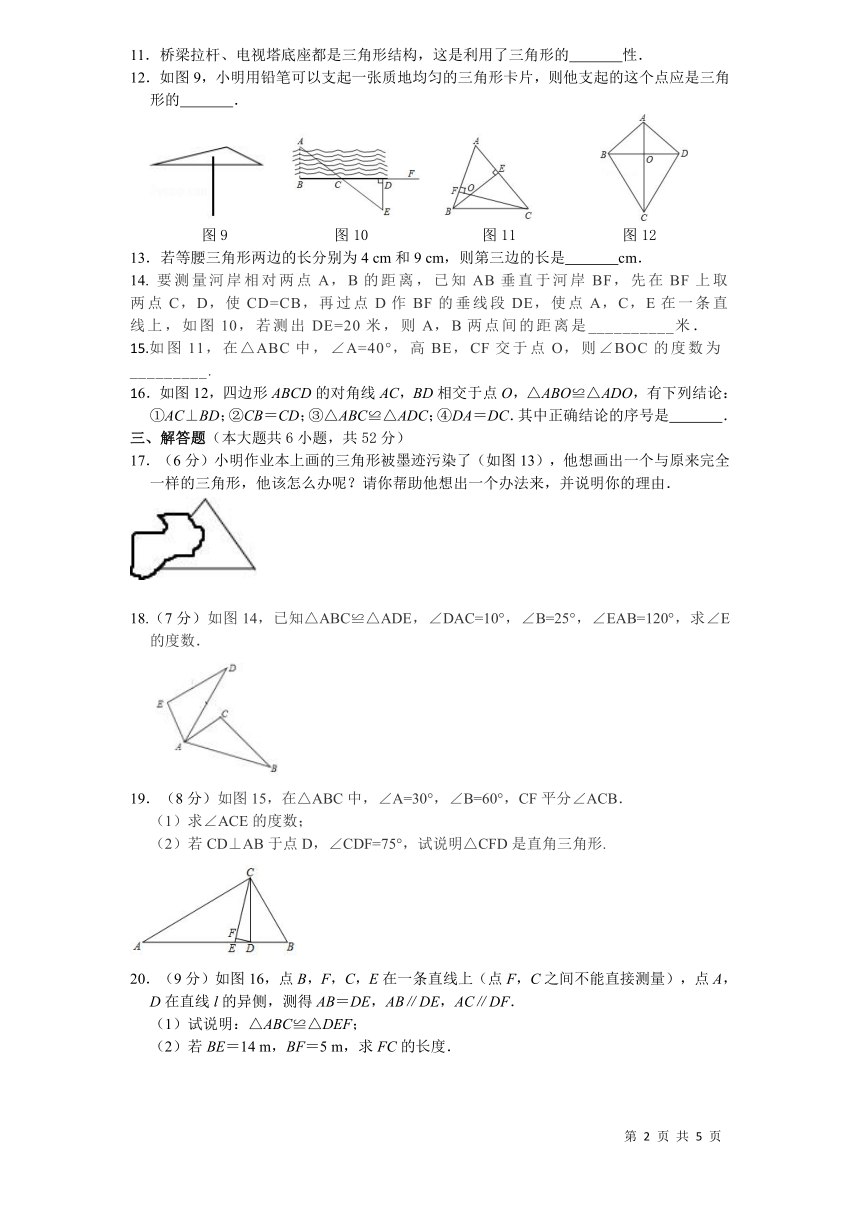
12.如图9,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的
.
图9
图10
图11
图12
13.若等腰三角形两边的长分别为4
cm和9
cm,则第三边的长是
cm.
14.
要测量河岸相对两点A,B的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图10,若测出DE=20米,则A,B两点间的距离是__________米.
15.如图11,在△ABC中,∠A=40°,高BE,CF交于点O,则∠BOC的度数为_________.
16.如图12,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO,有下列结论:
①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中正确结论的序号是
.
三、解答题(本大题共6小题,共52分)
17.(6分)小明作业本上画的三角形被墨迹污染了(如图13),他想画出一个与原来完全一样的三角形,他该怎么办呢?请你帮助他想出一个办法来,并说明你的理由.
18.(7分)如图14,已知△ABC≌△ADE,∠DAC=10°,∠B=25°,∠EAB=120°,求∠E的度数.
19.(8分)如图15,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.
(1)求∠ACE的度数;
(2)若CD⊥AB于点D,∠CDF=75°,试说明△CFD是直角三角形.
20.(9分)如图16,点B,F,C,E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)试说明:△ABC≌△DEF;
(2)若BE=14
m,BF=5
m,求FC的长度.
21.(10分)如图17,在△ABC中,AB=AC,D是BC的中点,E在AD上.
(1)△ABD和△ACD全等吗?为什么?还有其他全等三角形吗?请直接写出其他全等的三角形,不用说明理由;
(2)为了吃到点E处的食物,甲、乙两只蜗牛同时从A点出发,甲沿线路“A→B→E”、乙沿线路“A→C→E”爬行,若它们爬行的速度相同,那么谁先能吃到食物呢?为什么?
22.(12分)如图18,在△ABC中,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD,CE交于点F,CD=CG,连接FG.
(1)试说明:FD=FG;
(2)线段FG与FE之间有怎样的数量关系,请说明理由.
附加题(20分,不计入总分)
如图①,已知AB=7
cm,AC⊥AB,BD⊥AB,垂足分别为A,B,AC=5
cm.点P在线段AB上以2
cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t
s.(当点P运动结束时,点Q运动随之结束)
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图②,若把“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为
x
cm/s,其他条件不变,当点P,Q运动到某处时,有△ACP与△BPQ全等,求出相应的x,t的值.
参考答案
一、
1.C
2.B
3.D
4.A
5.C
6.C
7.C
8.A
9.C
10.D
二、11.稳定
12.重心
13.9
14.20
15.140°
16.①②③
三、17.解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形,如图所示,所作△ABC是与原来完全一样的三角形.
18.解:因为△ABC≌△ADE,所以∠D=∠B=25°,∠BAC=∠DAE.
因为∠EAB=120°,所以∠DAE+∠CAD+∠BAC=120°.
因为∠CAD=10°,所以∠DAE=×(120°-10°)=55°.
所以∠E=180°-25°-55°=100°.
19.解:(1)因为在△ABC中,∠A=30°,∠B=60°,所以∠ACB=180°-30°-60°=90°.
又因为CF平分∠ACB,所以∠ACE=∠ACB=45°.
(2)因为CD⊥AB,∠B=60°,所以∠BCD=90°-60°=30°.
又因为∠BCE=∠ACE=45°,所以∠DCF=∠BCE-∠BCD=15°.
因为∠CDF=75°,所以∠CFD=180°-75°-15°=90°.
所以△CFD是直角三角形.
20.(1)因为AB∥DE,所以∠ABC=∠DEF.因为AC∥DF,所以∠ACB=∠DFE.
在△ABC和△DEF中,因为∠ABC=∠DEF,∠ACB=∠DFE,AB=DE,
所以△ABC≌△DEF.
(2)因为△ABC≌△DEF,所以BC=EF.所以BF+FC=EC+FC.所以BF=EC.
因为BE=14,BF=5,所以FC=14﹣5﹣5=4(m).
21.解:(1)△ABD≌△ACD.理由如下:
因为D是BC的中点,所以BD=CD.
在△ABD和△ACD中,因为AB=AC,BD=CD,AD=AD,
所以△ABD≌△ACD.
另外还有△BDE≌△CDE,△ABE≌△ACE.
(2)甲、乙两只蜗牛同时吃到食物.理由如下:
由(1)知△ABD≌△ACD,所以∠BAD=∠CAD.
在△ABE和△ACE中,因为AB=AC,∠BAE=∠CAE,AE=AE,
所以△ABE≌△ACE
.所以BE=CE.所以AB+BE=AC+CE.
因为两只蜗牛的爬行速度相同,所以它们同时到达点E,同时吃到食物.
22.
解:(1)因为CE平分∠ACB,所以∠FCD=∠FCG.
在△CFD和△CFG中,因为CD=CG,∠FCD=∠FCG,CF=CF,
所以△CFD≌△CFG.所以FD=FG.
(2)FG=FE.
理由:因为∠B=60°,所以∠BAC+∠BCA=120°.
因为AD平分∠BAC,CE平分∠BCA,所以∠ACF+∠FAC=(∠BCA+∠BAC)=60°.
所以∠AFC=120°.所以∠CFD=∠AFE=60°.
因为△CFD≌△CFG,所以∠CFD=∠CFG=60°.所以∠AFG=∠AFE=60°.
在△AFG和△AFE中,因为∠AFG=∠AFE,AF=AF,∠FAG=∠FAE,
所以△AFG≌△AFE.所以FG=FE.
附加题
解:(1)△ACP≌△BPQ.
因为AC⊥AB,BD⊥AB,所以∠A=∠B=90°.
因为AP=BQ=2,所以BP=5.所以BP=AC.
在△ACP和△BPQ中,因为AP=BQ,∠A=∠B,AC=BP,
所以△ACP≌△BPQ.所以∠C=∠BPQ.
因为∠C+∠APC=90°,所以∠APC+∠BPQ=90°.所以∠CPQ=90°.所以PC⊥PQ.
(2)若△ACP≌△BPQ,则AC=BP,AP=BQ,可得5=7-2t,2t=xt.解得x=2,t=1;
若△ACP≌△BQP,则AC=BQ,AP=BP,可得5=xt,2t=7-2t.解得x=,t=.
第
7
页
共
8
页
三角形综合测评
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.以下列各组线段为边,能组成三角形的是( )
A.2
cm,5
cm,8
cm
B.3
cm,3
cm,6
cm
C.3
cm,4
cm,5
cm
D.1
cm,2
cm,3
cm
2.下列四个图形中,△ABC的边AB上的高线画法正确的是( )
A
B
C
D
3.如图1,在△ABC中,∠B=55°,∠C=63°,DE∥AB,则∠DEC的度数为( )
A.63°
B.113°
C.55°
D.62°
图1
图2
图3
图4
如图2,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是( A )
A.9
B.14
C.16
D.不能确定
5.如图3,已知MB=ND,∠MBA=∠NDC,添加下列一个条件后仍不能判定△ABM≌△CDN的是( )
A.∠M=∠N
B.AB=CD
C.AM=CN
D.AM∥CN
6.要测量圆形工件的外径,工人师傅设计了如图4所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则这个工件的外径必是CD的长,其依据的是三角形全等的判定条件( )
A.ASA
B.AAS
C.SAS
D.SSS
7.如图5,△ABC≌△ADE,若∠B=70°,∠C=30°,∠DAC=25°,则∠EAC的度数为( )
A.70°
B.80°
C.55°
D.45°
图5
图6
图7
图8
8.如图6,已知OA=OB,OC=OD,若∠O=50°,∠D=35°,则∠OBC的度数为( )
A.95°
B.120°
C.50°
D.105°
9.如图7,在△ABC中,∠B=∠C=65°,BD=CE,BE=CF,则∠DEF的度数是( C )
A.75°
B.70°
C.65°
D.60°
10.如图8,∠BAC=∠ACD=90°,∠ABC=∠D,CE⊥AD,且BE平分∠ABC,有下列结论:①AD=CB;②∠ACE=∠ABC;③AB=CD;④∠CEF=∠CFE.其中正确的是( )
A.仅①③
B.仅①③④
C.仅①②③
D.①②③④
二、填空题(本大题共6小题,每小题3分,共18分)
11.桥梁拉杆、电视塔底座都是三角形结构,这是利用了三角形的
性.
12.如图9,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的
.
图9
图10
图11
图12
13.若等腰三角形两边的长分别为4
cm和9
cm,则第三边的长是
cm.
14.
要测量河岸相对两点A,B的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图10,若测出DE=20米,则A,B两点间的距离是__________米.
15.如图11,在△ABC中,∠A=40°,高BE,CF交于点O,则∠BOC的度数为_________.
16.如图12,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO,有下列结论:
①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中正确结论的序号是
.
三、解答题(本大题共6小题,共52分)
17.(6分)小明作业本上画的三角形被墨迹污染了(如图13),他想画出一个与原来完全一样的三角形,他该怎么办呢?请你帮助他想出一个办法来,并说明你的理由.
18.(7分)如图14,已知△ABC≌△ADE,∠DAC=10°,∠B=25°,∠EAB=120°,求∠E的度数.
19.(8分)如图15,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.
(1)求∠ACE的度数;
(2)若CD⊥AB于点D,∠CDF=75°,试说明△CFD是直角三角形.
20.(9分)如图16,点B,F,C,E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)试说明:△ABC≌△DEF;
(2)若BE=14
m,BF=5
m,求FC的长度.
21.(10分)如图17,在△ABC中,AB=AC,D是BC的中点,E在AD上.
(1)△ABD和△ACD全等吗?为什么?还有其他全等三角形吗?请直接写出其他全等的三角形,不用说明理由;
(2)为了吃到点E处的食物,甲、乙两只蜗牛同时从A点出发,甲沿线路“A→B→E”、乙沿线路“A→C→E”爬行,若它们爬行的速度相同,那么谁先能吃到食物呢?为什么?
22.(12分)如图18,在△ABC中,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD,CE交于点F,CD=CG,连接FG.
(1)试说明:FD=FG;
(2)线段FG与FE之间有怎样的数量关系,请说明理由.
附加题(20分,不计入总分)
如图①,已知AB=7
cm,AC⊥AB,BD⊥AB,垂足分别为A,B,AC=5
cm.点P在线段AB上以2
cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t
s.(当点P运动结束时,点Q运动随之结束)
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图②,若把“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为
x
cm/s,其他条件不变,当点P,Q运动到某处时,有△ACP与△BPQ全等,求出相应的x,t的值.
参考答案
一、
1.C
2.B
3.D
4.A
5.C
6.C
7.C
8.A
9.C
10.D
二、11.稳定
12.重心
13.9
14.20
15.140°
16.①②③
三、17.解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形,如图所示,所作△ABC是与原来完全一样的三角形.
18.解:因为△ABC≌△ADE,所以∠D=∠B=25°,∠BAC=∠DAE.
因为∠EAB=120°,所以∠DAE+∠CAD+∠BAC=120°.
因为∠CAD=10°,所以∠DAE=×(120°-10°)=55°.
所以∠E=180°-25°-55°=100°.
19.解:(1)因为在△ABC中,∠A=30°,∠B=60°,所以∠ACB=180°-30°-60°=90°.
又因为CF平分∠ACB,所以∠ACE=∠ACB=45°.
(2)因为CD⊥AB,∠B=60°,所以∠BCD=90°-60°=30°.
又因为∠BCE=∠ACE=45°,所以∠DCF=∠BCE-∠BCD=15°.
因为∠CDF=75°,所以∠CFD=180°-75°-15°=90°.
所以△CFD是直角三角形.
20.(1)因为AB∥DE,所以∠ABC=∠DEF.因为AC∥DF,所以∠ACB=∠DFE.
在△ABC和△DEF中,因为∠ABC=∠DEF,∠ACB=∠DFE,AB=DE,
所以△ABC≌△DEF.
(2)因为△ABC≌△DEF,所以BC=EF.所以BF+FC=EC+FC.所以BF=EC.
因为BE=14,BF=5,所以FC=14﹣5﹣5=4(m).
21.解:(1)△ABD≌△ACD.理由如下:
因为D是BC的中点,所以BD=CD.
在△ABD和△ACD中,因为AB=AC,BD=CD,AD=AD,
所以△ABD≌△ACD.
另外还有△BDE≌△CDE,△ABE≌△ACE.
(2)甲、乙两只蜗牛同时吃到食物.理由如下:
由(1)知△ABD≌△ACD,所以∠BAD=∠CAD.
在△ABE和△ACE中,因为AB=AC,∠BAE=∠CAE,AE=AE,
所以△ABE≌△ACE
.所以BE=CE.所以AB+BE=AC+CE.
因为两只蜗牛的爬行速度相同,所以它们同时到达点E,同时吃到食物.
22.
解:(1)因为CE平分∠ACB,所以∠FCD=∠FCG.
在△CFD和△CFG中,因为CD=CG,∠FCD=∠FCG,CF=CF,
所以△CFD≌△CFG.所以FD=FG.
(2)FG=FE.
理由:因为∠B=60°,所以∠BAC+∠BCA=120°.
因为AD平分∠BAC,CE平分∠BCA,所以∠ACF+∠FAC=(∠BCA+∠BAC)=60°.
所以∠AFC=120°.所以∠CFD=∠AFE=60°.
因为△CFD≌△CFG,所以∠CFD=∠CFG=60°.所以∠AFG=∠AFE=60°.
在△AFG和△AFE中,因为∠AFG=∠AFE,AF=AF,∠FAG=∠FAE,
所以△AFG≌△AFE.所以FG=FE.
附加题
解:(1)△ACP≌△BPQ.
因为AC⊥AB,BD⊥AB,所以∠A=∠B=90°.
因为AP=BQ=2,所以BP=5.所以BP=AC.
在△ACP和△BPQ中,因为AP=BQ,∠A=∠B,AC=BP,
所以△ACP≌△BPQ.所以∠C=∠BPQ.
因为∠C+∠APC=90°,所以∠APC+∠BPQ=90°.所以∠CPQ=90°.所以PC⊥PQ.
(2)若△ACP≌△BPQ,则AC=BP,AP=BQ,可得5=7-2t,2t=xt.解得x=2,t=1;
若△ACP≌△BQP,则AC=BQ,AP=BP,可得5=xt,2t=7-2t.解得x=,t=.
第
7
页
共
8
页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
