2020~2021学年人教版八年级数学下册第十八章 平行四边形测试题(word版,含答案)
文档属性
| 名称 | 2020~2021学年人教版八年级数学下册第十八章 平行四边形测试题(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 175.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-13 22:22:16 | ||
图片预览


文档简介
第十八章
平行四边形测试题
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.
在□ABCD中,已知AD=6
cm,AB=4
cm,则□ABCD的周长为(
)
A.
6
cm
B.
10
cm
C.
12
cm
D.
20
cm
2.
如图1,在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数等于(
)
A.
45°
B.
55°
C.
65°
D.
75°
图1
图2
图3
3.
如图2,AD,CE是△ABC的高,过点A作AF∥BC,则下列线段的长能表示图中两条平行线之间的距离的是( )
A.
AB
B.
AD
C.
CE
D.
AC
4.
如图3,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3)
B.(3,6)
C.(0,6)
D.(6,6)
5.
如图4,在□ABCD中,EG∥FH∥CD,则图中所有的平行四边形有( )
A.
3个
B.
4个
C.
5个
D.
6个
图4
图5
6.
已知□ABCD,根据图5中尺规作图的痕迹,判断下列结论不一定成立的是(
)
A.
∠DAE=∠BAE
B.
∠DEA=∠DAB
C.
DE=BE
D.
BC=DE
7.(2020年连云港)如图6,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.
66°
B.
60°
C.
57°
D.
48°
图6
图7
图8
8.
下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程错误的是( )
A.
由①推出②
B.
由③推出①
C.
由②推出③
D.
由②推出①
9.
如图7,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB.则四边形ABCD的面积为( )
A.
40
B.
24
C.
20
D.
15
10.
如图8,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF中点,则AM的最小值为( )
A.
1
B.
1.3
C.
1.2
D.
1.5
二、填空题(本大题共6小题,每小题3分,共18分)
11.
小玲的爸爸在钉制平行四边形框架时,采用了一种方法,如图9所示,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是
.
图9
图10
图11
12.
如图10,矩形ABCD的对角线AC与BD相交于点O,∠AOB=120°,AD=5,则AC的长是
.
13.
有下列条件:①AB=CD,②AD=BC,③AB∥CD,④AD∥BC.请从中任选两个,使它们能判定四边形ABCD是平行四边形,则共有
种情况符合要求.
14.
如图11,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为
.
15.
如图12,四边形ABCD和四边形ACEF都是平行四边形,EF经过点D,若□ABCD的面积为S1,□ACEF的面积为S2,则S1
S2.(填“>”“<”或“=”)
图12
图13
16.
如图13,在四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,若BF⊥CD,AD=5
cm,AF=18
cm,四边形ABCF的周长为
cm.
三、解答题(本大题共7小题,共52分)
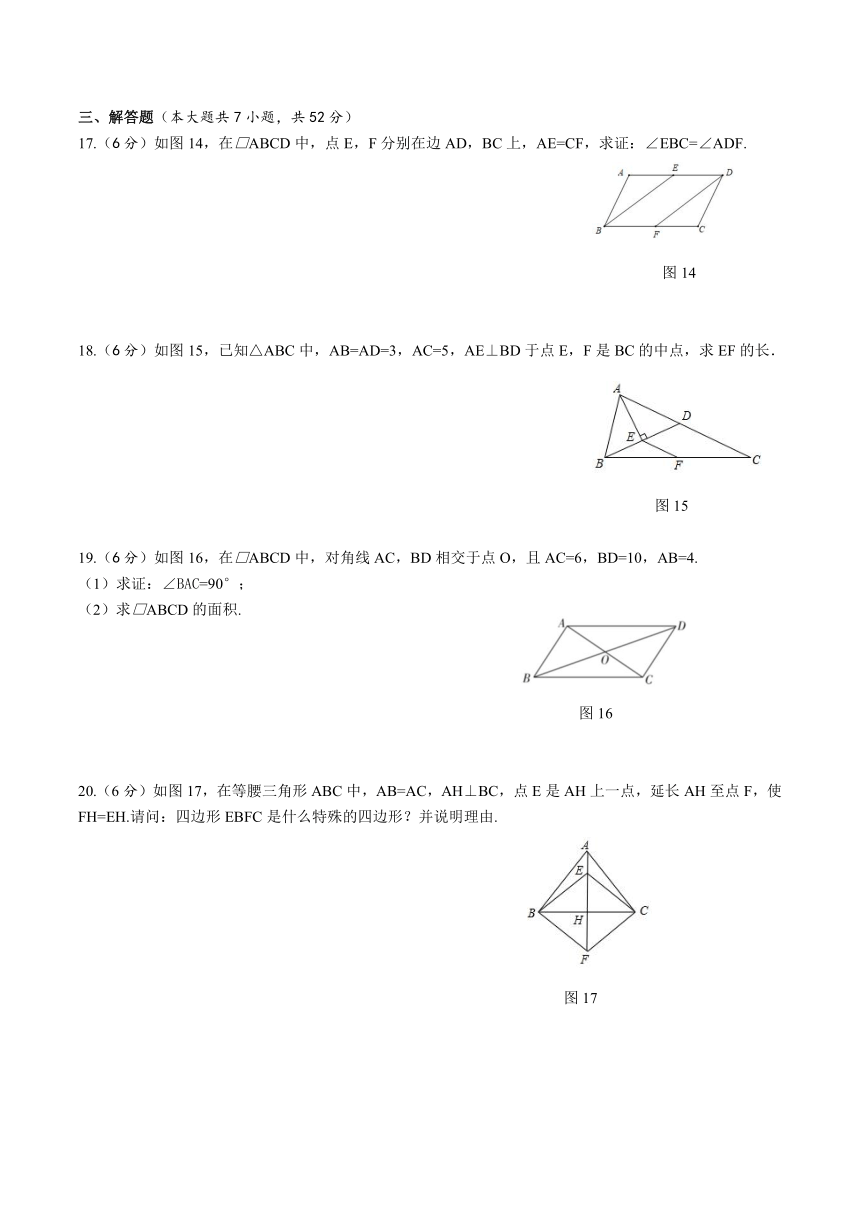
17.(6分)如图14,在□ABCD中,点E,F分别在边AD,BC上,AE=CF,求证:∠EBC=∠ADF.
图14
18.(6分)如图15,已知△ABC中,AB=AD=3,AC=5,AE⊥BD于点E,F是BC的中点,求EF的长.
图15
19.(6分)如图16,在□ABCD中,对角线AC,BD相交于点O,且AC=6,BD=10,AB=4.
(1)求证:∠BAC=90°;
(2)求□ABCD的面积.
图16
20.(6分)如图17,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.请问:四边形EBFC是什么特殊的四边形?并说明理由.
图17
21.(8分)如图18,正方形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.
(1)求证:四边形OCED是正方形.
(2)若AC=,求点E到边AB的距离.
图18
22.(10分)如图19,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
图19
23.
(10分)如图20,在四边形ABCD中,AD∥BC,∠B=90°,AB=8
cm,AD=20
cm,BC=24
cm,点P,Q分别从A,C同时出发,向点D,B运动.当一个点到达端点时,停止运动,另一个点也停止运动.
(1)如果P,Q的运动速度分别为1
cm/s和3
cm/s.运动时间为t
s,当t为何值时,直线PQ能将四边形ABCD截出一个平行四边形?请说明理由.
(2)如果P的运动速度为1
cm/s,其他条件不变,要使四边形APQB是矩形,且矩形的长、宽之比为2∶1,求点Q的运动速度.
图20
附加题(20分,不计入总分)
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图①所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
(1)请根据图①完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+
S△FGC),S矩形EBMF=S△ABC-(
+
).
易知,S△ADC=
S△ABC,
=
,
=
.
所以S矩形NFGD=S矩形EBMF.
(2)如图②,点P是矩形ABCD的对角线BD上一点,过点P作EF∥BC分别交AB,CD于点E,F,连接PA,PC.若PE=5,DF=4,求图中阴影部分的面积.
①
②
第十八章
平行四边形测试题
一、1.
D
2.
A
3.
B
4.
D
5.
D
6.
C
7.
C
8.
A
9.
B
10.
C
二、11.
对角线互相平分的四边形是平行四边形
12.
10
13.
四
14.
22.5°
15.
=
16.
56
三、17.
证明:因为四边形ABCD是平行四边形,所以AD=BC,AD∥BC.
因为AE=CF,所以DE=BF.
又DE∥BF,所以四边形BEDF是平行四边形.
所以∠EBC=∠ADF.
18.
解:因为AB=AD,
AE⊥BD,所以E是BD的中点.
所以CD=AC-AD=5-3=2.
又F是BC的中点,所以EF是△BCD的中位线.
所以EF=CD=1.
19.(1)证明:因为四边形ABCD是平行四边形,所以AO=AC=3,BO=BD=5.
又AB=4,所以AO2+AB2=
BO2.
所以△BAO是直角三角形,且∠BAO=90°,即∠BAC=90°.
(2)解:S□ABCD=2S△ABC=2××6×4
=24.
所以□ABCD的面积为24.
20.
解:四边形EBFC是菱形.理由如下:
因为AB=AC,AH⊥BC,所以BH=CH.
因为FH=EH,所以四边形EBFC是平行四边形.
又因为AH⊥BC,所以□EBFC是菱形.
21.
(1)证明:因为CE∥BD,DE∥AC,所以四边形OCED是平行四边形.
在正方形ABCD中,AC⊥BD,OD=OC,所以∠COD=90°.
所以□OCED是正方形.
(2)解:如图,连接EO并延长,交AB于点G,交CD于点H.
由(1)知四边形OCED是正方形,所以CD⊥OE.
因为四边形ABCD是正方形,所以AB∥CD.所以EG⊥AB.
因为AC=,所以AB2+BC2=2,即2AB2=2,AB=1.
所以AB=BC=CD=OE=1,GO=BC=0.5.
所以EG=OE+
GO=1+0.5=1.5.
所以点E到边AB的距离为1.5.
22.
解:(1)因为四边形ABCD是菱形,所以OD=OB.
又E是AD的中点,所以OE是△ABD的中位线.所以OE∥FG.
又EF∥OG所以四边形EFOG是平行四边形.
因为EF⊥AB,所以∠EFG=90°.
所以□OEFG是矩形.
(2)因为四边形ABCD是菱形,所以BD⊥AC,AB=AD=10。
所以OE=AE=AD=5.
因为四边形OEFG是矩形,所以FG=OE=5.
又EF=4,所以AF===3.
所以BG=AB-AF-FG=10-3-5=2.
23.
解:(1)当四边形PQCD是平行四边形时,PD=CQ,所以20-t=3t,解得t=5;
当四边形ABQP是平行四边形时,AP=BQ,所以t=24-3t,解得t=6.
所以当t=5
s或t=6
s时,直线PQ能将四边形ABCD截出一个平行四边形.
(2)设点Q的运动速度为x
cm/s.
因为四边形APQB是矩形,且矩形的长、宽之比为2∶1,所以PA=BQ=4或PA=BQ=16,即t=4或t=16.
所以24-4x=4,解得x=5.
或24-16x=16,解得x=.
所以点Q的运动速度为5
cm/s或
cm/s.
附加题
解:(1)S△AEF
S△FMC
S△ANF
S△AEF
S△FMC
S△FGC
(2)如图,作PM⊥AD于点M,交BC于点N.
则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形.
所以AE=MP=DF=4.
同(1),得S矩形AEPM=S矩形CFPN.
所以S△AEP=S△AMP,S△CFP=S△CNP.
所以S△AEP=S△CFP=PE·AE=×5×4=10.
所以S阴影=S△AEP+S△CFP=10+10=20.
平行四边形测试题
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.
在□ABCD中,已知AD=6
cm,AB=4
cm,则□ABCD的周长为(
)
A.
6
cm
B.
10
cm
C.
12
cm
D.
20
cm
2.
如图1,在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数等于(
)
A.
45°
B.
55°
C.
65°
D.
75°
图1
图2
图3
3.
如图2,AD,CE是△ABC的高,过点A作AF∥BC,则下列线段的长能表示图中两条平行线之间的距离的是( )
A.
AB
B.
AD
C.
CE
D.
AC
4.
如图3,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3)
B.(3,6)
C.(0,6)
D.(6,6)
5.
如图4,在□ABCD中,EG∥FH∥CD,则图中所有的平行四边形有( )
A.
3个
B.
4个
C.
5个
D.
6个
图4
图5
6.
已知□ABCD,根据图5中尺规作图的痕迹,判断下列结论不一定成立的是(
)
A.
∠DAE=∠BAE
B.
∠DEA=∠DAB
C.
DE=BE
D.
BC=DE
7.(2020年连云港)如图6,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.
66°
B.
60°
C.
57°
D.
48°
图6
图7
图8
8.
下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程错误的是( )
A.
由①推出②
B.
由③推出①
C.
由②推出③
D.
由②推出①
9.
如图7,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB.则四边形ABCD的面积为( )
A.
40
B.
24
C.
20
D.
15
10.
如图8,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF中点,则AM的最小值为( )
A.
1
B.
1.3
C.
1.2
D.
1.5
二、填空题(本大题共6小题,每小题3分,共18分)
11.
小玲的爸爸在钉制平行四边形框架时,采用了一种方法,如图9所示,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是
.
图9
图10
图11
12.
如图10,矩形ABCD的对角线AC与BD相交于点O,∠AOB=120°,AD=5,则AC的长是
.
13.
有下列条件:①AB=CD,②AD=BC,③AB∥CD,④AD∥BC.请从中任选两个,使它们能判定四边形ABCD是平行四边形,则共有
种情况符合要求.
14.
如图11,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为
.
15.
如图12,四边形ABCD和四边形ACEF都是平行四边形,EF经过点D,若□ABCD的面积为S1,□ACEF的面积为S2,则S1
S2.(填“>”“<”或“=”)
图12
图13
16.
如图13,在四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,若BF⊥CD,AD=5
cm,AF=18
cm,四边形ABCF的周长为
cm.
三、解答题(本大题共7小题,共52分)
17.(6分)如图14,在□ABCD中,点E,F分别在边AD,BC上,AE=CF,求证:∠EBC=∠ADF.
图14
18.(6分)如图15,已知△ABC中,AB=AD=3,AC=5,AE⊥BD于点E,F是BC的中点,求EF的长.
图15
19.(6分)如图16,在□ABCD中,对角线AC,BD相交于点O,且AC=6,BD=10,AB=4.
(1)求证:∠BAC=90°;
(2)求□ABCD的面积.
图16
20.(6分)如图17,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.请问:四边形EBFC是什么特殊的四边形?并说明理由.
图17
21.(8分)如图18,正方形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.
(1)求证:四边形OCED是正方形.
(2)若AC=,求点E到边AB的距离.
图18
22.(10分)如图19,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
图19
23.
(10分)如图20,在四边形ABCD中,AD∥BC,∠B=90°,AB=8
cm,AD=20
cm,BC=24
cm,点P,Q分别从A,C同时出发,向点D,B运动.当一个点到达端点时,停止运动,另一个点也停止运动.
(1)如果P,Q的运动速度分别为1
cm/s和3
cm/s.运动时间为t
s,当t为何值时,直线PQ能将四边形ABCD截出一个平行四边形?请说明理由.
(2)如果P的运动速度为1
cm/s,其他条件不变,要使四边形APQB是矩形,且矩形的长、宽之比为2∶1,求点Q的运动速度.
图20
附加题(20分,不计入总分)
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图①所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
(1)请根据图①完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+
S△FGC),S矩形EBMF=S△ABC-(
+
).
易知,S△ADC=
S△ABC,
=
,
=
.
所以S矩形NFGD=S矩形EBMF.
(2)如图②,点P是矩形ABCD的对角线BD上一点,过点P作EF∥BC分别交AB,CD于点E,F,连接PA,PC.若PE=5,DF=4,求图中阴影部分的面积.
①
②
第十八章
平行四边形测试题
一、1.
D
2.
A
3.
B
4.
D
5.
D
6.
C
7.
C
8.
A
9.
B
10.
C
二、11.
对角线互相平分的四边形是平行四边形
12.
10
13.
四
14.
22.5°
15.
=
16.
56
三、17.
证明:因为四边形ABCD是平行四边形,所以AD=BC,AD∥BC.
因为AE=CF,所以DE=BF.
又DE∥BF,所以四边形BEDF是平行四边形.
所以∠EBC=∠ADF.
18.
解:因为AB=AD,
AE⊥BD,所以E是BD的中点.
所以CD=AC-AD=5-3=2.
又F是BC的中点,所以EF是△BCD的中位线.
所以EF=CD=1.
19.(1)证明:因为四边形ABCD是平行四边形,所以AO=AC=3,BO=BD=5.
又AB=4,所以AO2+AB2=
BO2.
所以△BAO是直角三角形,且∠BAO=90°,即∠BAC=90°.
(2)解:S□ABCD=2S△ABC=2××6×4
=24.
所以□ABCD的面积为24.
20.
解:四边形EBFC是菱形.理由如下:
因为AB=AC,AH⊥BC,所以BH=CH.
因为FH=EH,所以四边形EBFC是平行四边形.
又因为AH⊥BC,所以□EBFC是菱形.
21.
(1)证明:因为CE∥BD,DE∥AC,所以四边形OCED是平行四边形.
在正方形ABCD中,AC⊥BD,OD=OC,所以∠COD=90°.
所以□OCED是正方形.
(2)解:如图,连接EO并延长,交AB于点G,交CD于点H.
由(1)知四边形OCED是正方形,所以CD⊥OE.
因为四边形ABCD是正方形,所以AB∥CD.所以EG⊥AB.
因为AC=,所以AB2+BC2=2,即2AB2=2,AB=1.
所以AB=BC=CD=OE=1,GO=BC=0.5.
所以EG=OE+
GO=1+0.5=1.5.
所以点E到边AB的距离为1.5.
22.
解:(1)因为四边形ABCD是菱形,所以OD=OB.
又E是AD的中点,所以OE是△ABD的中位线.所以OE∥FG.
又EF∥OG所以四边形EFOG是平行四边形.
因为EF⊥AB,所以∠EFG=90°.
所以□OEFG是矩形.
(2)因为四边形ABCD是菱形,所以BD⊥AC,AB=AD=10。
所以OE=AE=AD=5.
因为四边形OEFG是矩形,所以FG=OE=5.
又EF=4,所以AF===3.
所以BG=AB-AF-FG=10-3-5=2.
23.
解:(1)当四边形PQCD是平行四边形时,PD=CQ,所以20-t=3t,解得t=5;
当四边形ABQP是平行四边形时,AP=BQ,所以t=24-3t,解得t=6.
所以当t=5
s或t=6
s时,直线PQ能将四边形ABCD截出一个平行四边形.
(2)设点Q的运动速度为x
cm/s.
因为四边形APQB是矩形,且矩形的长、宽之比为2∶1,所以PA=BQ=4或PA=BQ=16,即t=4或t=16.
所以24-4x=4,解得x=5.
或24-16x=16,解得x=.
所以点Q的运动速度为5
cm/s或
cm/s.
附加题
解:(1)S△AEF
S△FMC
S△ANF
S△AEF
S△FMC
S△FGC
(2)如图,作PM⊥AD于点M,交BC于点N.
则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形.
所以AE=MP=DF=4.
同(1),得S矩形AEPM=S矩形CFPN.
所以S△AEP=S△AMP,S△CFP=S△CNP.
所以S△AEP=S△CFP=PE·AE=×5×4=10.
所以S阴影=S△AEP+S△CFP=10+10=20.
