6.4.3 正弦定理-课件(共20张PPT)
文档属性
| 名称 | 6.4.3 正弦定理-课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 21:21:41 | ||
图片预览








文档简介
第6章 平面向量及其应用
6.4.3 正弦定理
????????????????????=????????????????????=????????????????????=????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
????????????????:????????????????:????????????????=????:????:????
?
????+????+????????????????????+????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????????
?
高中数学人教A版(2019)必修 第二册
正弦定理
正弦定理的描述
【文字语言】在一个三角形中,各边的长度和它所对的角的正弦的比相等
适用范围:任意的三角形
结构特征:分式连等形式,各边与其对角的正弦严格对应,体现了数学的对称之美.
简单应用:实现三角形中边角关系的转化
【符号语言】如图,在ΔABC中,????????????????????=????????????????????=????????????????????=2????(????是????????????????外接圆半径)
?
????
?
????
?
????
?
????
?
????
?
????
?
探究新知
正弦定理
正弦定理的应用
已知两角和任一边,求其他的边和角
——考什么
已知两边和其中一边的对角,求其他边和角
——怎么考
作为知识形态,放在选择题,填空题中考
大题考察正弦定理,常与三角函数,三角恒等变换结合,考察工具形态
边角互相转化
探究新知
正弦定理
正弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【证法1】定义法(利用三角函数的定义)
教材中给出了当ΔABC为直角三角形时正弦定理的证明,现在我们给出当ΔABC为钝角三角形时的证明
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,设∠ABC为钝角,过点C作AB的垂线与AB的延长线交于点D.
由三角函数的定义可知????????=????????????????????????,????????=?????????????????????????∠????????????=????????????????????∠????????????
?
即有????????????????????????=????????????????????∠????????????,即????????????????????∠????????????=????????????????????????,同理可得????????????????????∠????????????=????????????????????∠????????????
?
所以就有????????????????????∠????????????=????????????????????????=????????????????????∠????????????,同理也可以推出锐角三角形时亦成立
?
探究新知
正弦定理
正弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【证法2】向量法(利用向量的数量积定义)
教材中给出了当ΔABC为直角三角形时正弦定理的证明,现在我们给出当ΔABC为钝角三角形时的证明
????
?
????
?
????
?
????
?
从而????????????????????????????????=????????????????????????=????????????????????????,类似可推出当ΔABC为直角三角形时亦成立.
?
如图,当ΔABC为钝角三角形时,过点A作非零向量????⊥AC.由向量的加法可得AB=AC+CB,则?????·AB= ?????·(AC+CB),∴ ?????·AB= ?????·AC+ ?????·CB
?
即????????????????????????90°?∠????????????=0+?????????????????????????90°+????,整理得
????????????????????∠????????????=????????????????????????,即????????????????????????????????=????????????????????????,同理可得????????????????????????=????????????????????????
?
探究新知
下列有关正弦定理的叙述:
①正弦定理只适用于锐角三角形
②正弦定理不适用于直角三角形
③在某一确定的三角形中,各边与它所对角的正弦的比是定值
④在ΔABC中,若内角A,B,C所对的边分别为????,????,????,则A:B:C= ????:????:????
其中哪些是正确的?
?
【解】正弦定理适用于人以三角形,故①②不正确;
在ΔABC中,由正弦定理得????????????????????=????????????????????=????????????????????=2????.因为三角形确定,所以外接圆半径R为定值,③正确;
?
④不正确,如A=B=45°,C=90°,A:B:C≠????:????:????
?
针对训练
正弦定理
三角形中的隐含条件
在ΔABC中,内角A,B,C所对的边分别为????,????,????,外接圆半径为????,则:
?
????+????+????=????,??????????
????>?????????>?????????????????????>????????????????;?????+????>?????????????????????+????????????????>????????????????
?
????????????????+????=?????????????????;????????????????+????=??????????????????;????????????????+????????=???????????? ????2
?
ΔABC为锐角三角形,则????+????>????2?????>????2??????????????????????>????????????????,????????????????>????????????????
?
即在锐角三角形中,一个角的正弦值大于另一个角的余弦值.
探究新知
正弦定理
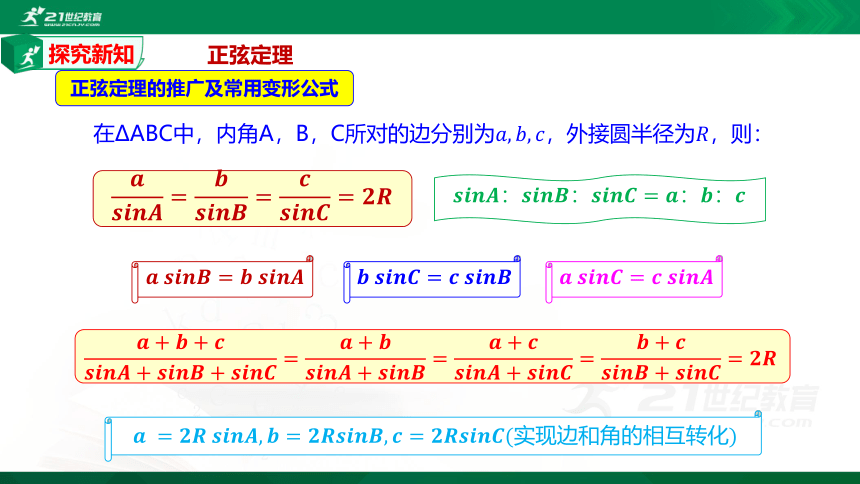
正弦定理的推广及常用变形公式
在ΔABC中,内角A,B,C所对的边分别为????,????,????,外接圆半径为????,则:
?
????????????????????=????????????????????=????????????????????=????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
????????????????:????????????????:????????????????=????:????:????
?
????+????+????????????????????+????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????????
?
?????=?????????????????????????,????=????????????????????????,????=????????????????????????(实现边和角的相互转化)
?
探究新知
利用正弦定理解三角形的类型及方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类型
已知条件
一般解法
已知三角形的两
角和任意一边
已知三角形的两边
和其中一边的对角
????=????????????????????????????????????,????=?????????+????,????=????????????????????????????????????
?
????,????,????
?
????,????,????
?
????,????,????
?
????,????,????
?
????=????????????????????????????????????,????=?????????+????,????=????????????????????????????????????
?
????=????????????????????????????????????,????=?????????+????,????=????????????????????????????????????
?
????????????????=????????????????????????,????=?????????+????,????=????????????????????????????????????
?
解的个数不唯一
①应用正弦定理解三角形时,必须明确三角形中边角之间的对应关系;
②已知两边和其中一边的对角解三角形时,解的个数不唯一确定, 需要讨论;
③解三角形时,要注意大边对大角这一性质的运用.
探究新知
解决几何问题的常见公式
在ΔABC中,内角A,B,C所对的边分别为?????,????,???? ——
?
三角形的高
在ΔABC中,边BC,CA,AB上的高分别记作?????,?????,?????
?
若ΔABC为锐角三角形,则由下图可知,????????=?????????????????????=?????????????????????
?
????
?
????
?
????
?
????
?
????
?
????
?
?????
?
????
?
????
?
????
?
????
?
????
?
????
?
?????
?
????
?
????
?
????
?
????
?
????
?
????
?
?????
?
同理可得?????????=?????????????????????=??????????????????????,????????=?????????????????????=?????????????????????
?
当ΔABC为直角三角形或钝角三角形时结论相同.
探究新知
解决几何问题的常见公式
在ΔABC中,内角A,B,C所对的边分别为?????,????,???? ——
?
三角形面积的计算公式
在ΔABC中,边BC,CA,AB上的高分别记作?????,?????,?????
?
????=????????????????????=????????????????????=????????????????????
?
????=?????????????????????????????????=?????????????????????????????????=?????????????????????????????????
?
对 的证明:
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
①当ΔABC为锐角三角形时,作AD⊥BC于点D,设
ΔABC的面积为S,则????=????????????????·????????=12?????????????????????????
?
②当ΔABC为钝角三角形时,作BC边上的高AD,
则????????=????????????????????????????????°?∠????????????=????????????????????∠????????????,∴????=12????????·????????=12?????????????????????????????????
?
当ΔABC为直角三角形时,上述结论依然成立.
探究新知
解决几何问题的常见公式
在ΔABC中,内角A,B,C所对的边分别为?????,????,???? ——
?
三角形面积的计算公式
在ΔABC中, ???? 为内切圆的半径,????为外接圆半径.
?
????=????????????+????+????·????
?
????=????????????????????
?
【证明】
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????????????????????=????????????????????+????????????????????+????????????????????
?
=????????????????+????????????????+????????????????=????????????+????+????·????
?
【证明】
????=?????????????????????????????????
=????????????????????????????
=????????????????????
?
探究新知
①在ΔABC中,内角A,B,C所对的边分别为?????,????,????,且????=5,????=4,????????????????=45,求ΔABC的面积.
?
【解】因为????????????????=45,????∈(0,????),∴ ????????????????=35
?
∴ ????????????????????=12?????????????????????????=12×5×4×35=6
?
②若锐角三角形ABC的面积为103,且AB=5,AC=8,求BC.
?
【解】由已知得12????????·????????·????????????????=20????????????????=103,????????????????=32
?
∵ ????∈0,????2所以????=????3,由余弦定理得
?
????????2=????????2+????????2?2????????·????????·????????????????=49,所以????????=7
?
针对训练
三角形的解的个数
已知三角形的两角和任意一边,求其他的边和角,此时第三角已知,三角形是唯一确定的,所以解是唯一的
已知三角形的两边和其中一边的对角,求其他的边和角,此时可能出现一解,两解或无解的情况,三角形不能被唯一确定.不妨设已知ΔABC的两边????,????和角A,作图步骤如下:
?
①先把未知边????画成水平的,作出已知角A;
角A的另一条边为已知边????;
?
②以边????的端点C为圆心, ????为半径作圆;
?
③观察圆C与边????交点的个数,就是三角形
解的个数.
?
????
?
????
?
????
?
????
?
探究新知
三角形的解的个数
显然,当A为锐角时,有如图所示的四种情况:
????
?
????
?
????
?
????
?
????
?
????
?
????无解
?
????
?
????
?
????
?
????
?
????
?
????
?
????=????????=????????????????????
仅有一个解
?
????
?
????
?
????
?
????
?
????
?
????
?
????????=????????????????????有两个解
?
????
?
????
?
????
?
????
?
????
?
????
?
????≥????
仅有一个解
?
探究新知
三角形的解的个数
当A为直角(或钝角)时,有如图所示的2种情况:
????
?
????
?
????
?
????
?
????
?
????>????
仅有一个解
?
????
?
????
?
????
?
????
?
????
?
????≤????
仅有一个解
?
根据分析可知,由于????,????
长度关系的不同,导致三角形有不同个数的解.若A为锐角,只有当????≥????????????????????时才有解,并且随着????的增大,得到的解的个数也不同;若A为钝角或直角,只有当????>????时才有解.
?
探究新知
三角形的解的个数
针对此类问题,我们有两种解决方法:
【1】正弦定理法(也称代数法或大边对大角法)
不妨设已知ΔABC的两边????,????和角A,根据正弦定理得????????????????????=????????????????????,可得????????????????=?????????????????????????.
?
①若????????????????>1,则三角形无解;
?
②若????????????????=1,则三角形有且仅有一个解;
?
③若0 大角),再求出B,从而确定三角形解的个数.
?
探究新知
三角形的解的个数
【2】公式法
不妨设已知ΔABC的两边????,????和角A,根据前面的分析可得三角形解的个数
的判断公式如下表:
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
?????
????≥????????°
?
????≥????
?
?????
??????????????????????
????=?????????????????????
?
?????
????>????
?
????≤????
?
一解
一解
两解
无解
一解
无解
探究新知
谢谢聆听
6.4.3 正弦定理
????????????????????=????????????????????=????????????????????=????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
????????????????:????????????????:????????????????=????:????:????
?
????+????+????????????????????+????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????????
?
高中数学人教A版(2019)必修 第二册
正弦定理
正弦定理的描述
【文字语言】在一个三角形中,各边的长度和它所对的角的正弦的比相等
适用范围:任意的三角形
结构特征:分式连等形式,各边与其对角的正弦严格对应,体现了数学的对称之美.
简单应用:实现三角形中边角关系的转化
【符号语言】如图,在ΔABC中,????????????????????=????????????????????=????????????????????=2????(????是????????????????外接圆半径)
?
????
?
????
?
????
?
????
?
????
?
????
?
探究新知
正弦定理
正弦定理的应用
已知两角和任一边,求其他的边和角
——考什么
已知两边和其中一边的对角,求其他边和角
——怎么考
作为知识形态,放在选择题,填空题中考
大题考察正弦定理,常与三角函数,三角恒等变换结合,考察工具形态
边角互相转化
探究新知
正弦定理
正弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【证法1】定义法(利用三角函数的定义)
教材中给出了当ΔABC为直角三角形时正弦定理的证明,现在我们给出当ΔABC为钝角三角形时的证明
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,设∠ABC为钝角,过点C作AB的垂线与AB的延长线交于点D.
由三角函数的定义可知????????=????????????????????????,????????=?????????????????????????∠????????????=????????????????????∠????????????
?
即有????????????????????????=????????????????????∠????????????,即????????????????????∠????????????=????????????????????????,同理可得????????????????????∠????????????=????????????????????∠????????????
?
所以就有????????????????????∠????????????=????????????????????????=????????????????????∠????????????,同理也可以推出锐角三角形时亦成立
?
探究新知
正弦定理
正弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【证法2】向量法(利用向量的数量积定义)
教材中给出了当ΔABC为直角三角形时正弦定理的证明,现在我们给出当ΔABC为钝角三角形时的证明
????
?
????
?
????
?
????
?
从而????????????????????????????????=????????????????????????=????????????????????????,类似可推出当ΔABC为直角三角形时亦成立.
?
如图,当ΔABC为钝角三角形时,过点A作非零向量????⊥AC.由向量的加法可得AB=AC+CB,则?????·AB= ?????·(AC+CB),∴ ?????·AB= ?????·AC+ ?????·CB
?
即????????????????????????90°?∠????????????=0+?????????????????????????90°+????,整理得
????????????????????∠????????????=????????????????????????,即????????????????????????????????=????????????????????????,同理可得????????????????????????=????????????????????????
?
探究新知
下列有关正弦定理的叙述:
①正弦定理只适用于锐角三角形
②正弦定理不适用于直角三角形
③在某一确定的三角形中,各边与它所对角的正弦的比是定值
④在ΔABC中,若内角A,B,C所对的边分别为????,????,????,则A:B:C= ????:????:????
其中哪些是正确的?
?
【解】正弦定理适用于人以三角形,故①②不正确;
在ΔABC中,由正弦定理得????????????????????=????????????????????=????????????????????=2????.因为三角形确定,所以外接圆半径R为定值,③正确;
?
④不正确,如A=B=45°,C=90°,A:B:C≠????:????:????
?
针对训练
正弦定理
三角形中的隐含条件
在ΔABC中,内角A,B,C所对的边分别为????,????,????,外接圆半径为????,则:
?
????+????+????=????,??????????
????>?????????>?????????????????????>????????????????;?????+????>?????????????????????+????????????????>????????????????
?
????????????????+????=?????????????????;????????????????+????=??????????????????;????????????????+????????=???????????? ????2
?
ΔABC为锐角三角形,则????+????>????2?????>????2??????????????????????>????????????????,????????????????>????????????????
?
即在锐角三角形中,一个角的正弦值大于另一个角的余弦值.
探究新知
正弦定理
正弦定理的推广及常用变形公式
在ΔABC中,内角A,B,C所对的边分别为????,????,????,外接圆半径为????,则:
?
????????????????????=????????????????????=????????????????????=????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
?????????????????????=?????????????????????
?
????????????????:????????????????:????????????????=????:????:????
?
????+????+????????????????????+????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????+????????????????????+????????????????=????????
?
?????=?????????????????????????,????=????????????????????????,????=????????????????????????(实现边和角的相互转化)
?
探究新知
利用正弦定理解三角形的类型及方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类型
已知条件
一般解法
已知三角形的两
角和任意一边
已知三角形的两边
和其中一边的对角
????=????????????????????????????????????,????=?????????+????,????=????????????????????????????????????
?
????,????,????
?
????,????,????
?
????,????,????
?
????,????,????
?
????=????????????????????????????????????,????=?????????+????,????=????????????????????????????????????
?
????=????????????????????????????????????,????=?????????+????,????=????????????????????????????????????
?
????????????????=????????????????????????,????=?????????+????,????=????????????????????????????????????
?
解的个数不唯一
①应用正弦定理解三角形时,必须明确三角形中边角之间的对应关系;
②已知两边和其中一边的对角解三角形时,解的个数不唯一确定, 需要讨论;
③解三角形时,要注意大边对大角这一性质的运用.
探究新知
解决几何问题的常见公式
在ΔABC中,内角A,B,C所对的边分别为?????,????,???? ——
?
三角形的高
在ΔABC中,边BC,CA,AB上的高分别记作?????,?????,?????
?
若ΔABC为锐角三角形,则由下图可知,????????=?????????????????????=?????????????????????
?
????
?
????
?
????
?
????
?
????
?
????
?
?????
?
????
?
????
?
????
?
????
?
????
?
????
?
?????
?
????
?
????
?
????
?
????
?
????
?
????
?
?????
?
同理可得?????????=?????????????????????=??????????????????????,????????=?????????????????????=?????????????????????
?
当ΔABC为直角三角形或钝角三角形时结论相同.
探究新知
解决几何问题的常见公式
在ΔABC中,内角A,B,C所对的边分别为?????,????,???? ——
?
三角形面积的计算公式
在ΔABC中,边BC,CA,AB上的高分别记作?????,?????,?????
?
????=????????????????????=????????????????????=????????????????????
?
????=?????????????????????????????????=?????????????????????????????????=?????????????????????????????????
?
对 的证明:
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
①当ΔABC为锐角三角形时,作AD⊥BC于点D,设
ΔABC的面积为S,则????=????????????????·????????=12?????????????????????????
?
②当ΔABC为钝角三角形时,作BC边上的高AD,
则????????=????????????????????????????????°?∠????????????=????????????????????∠????????????,∴????=12????????·????????=12?????????????????????????????????
?
当ΔABC为直角三角形时,上述结论依然成立.
探究新知
解决几何问题的常见公式
在ΔABC中,内角A,B,C所对的边分别为?????,????,???? ——
?
三角形面积的计算公式
在ΔABC中, ???? 为内切圆的半径,????为外接圆半径.
?
????=????????????+????+????·????
?
????=????????????????????
?
【证明】
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????????????????????=????????????????????+????????????????????+????????????????????
?
=????????????????+????????????????+????????????????=????????????+????+????·????
?
【证明】
????=?????????????????????????????????
=????????????????????????????
=????????????????????
?
探究新知
①在ΔABC中,内角A,B,C所对的边分别为?????,????,????,且????=5,????=4,????????????????=45,求ΔABC的面积.
?
【解】因为????????????????=45,????∈(0,????),∴ ????????????????=35
?
∴ ????????????????????=12?????????????????????????=12×5×4×35=6
?
②若锐角三角形ABC的面积为103,且AB=5,AC=8,求BC.
?
【解】由已知得12????????·????????·????????????????=20????????????????=103,????????????????=32
?
∵ ????∈0,????2所以????=????3,由余弦定理得
?
????????2=????????2+????????2?2????????·????????·????????????????=49,所以????????=7
?
针对训练
三角形的解的个数
已知三角形的两角和任意一边,求其他的边和角,此时第三角已知,三角形是唯一确定的,所以解是唯一的
已知三角形的两边和其中一边的对角,求其他的边和角,此时可能出现一解,两解或无解的情况,三角形不能被唯一确定.不妨设已知ΔABC的两边????,????和角A,作图步骤如下:
?
①先把未知边????画成水平的,作出已知角A;
角A的另一条边为已知边????;
?
②以边????的端点C为圆心, ????为半径作圆;
?
③观察圆C与边????交点的个数,就是三角形
解的个数.
?
????
?
????
?
????
?
????
?
探究新知
三角形的解的个数
显然,当A为锐角时,有如图所示的四种情况:
????
?
????
?
????
?
????
?
????
?
????
?
????无解
?
????
?
????
?
????
?
????
?
????
?
????
?
????=????????=????????????????????
仅有一个解
?
????
?
????
?
????
?
????
?
????
?
????
?
????????=????????????????????有两个解
?
????
?
????
?
????
?
????
?
????
?
????
?
????≥????
仅有一个解
?
探究新知
三角形的解的个数
当A为直角(或钝角)时,有如图所示的2种情况:
????
?
????
?
????
?
????
?
????
?
????>????
仅有一个解
?
????
?
????
?
????
?
????
?
????
?
????≤????
仅有一个解
?
根据分析可知,由于????,????
长度关系的不同,导致三角形有不同个数的解.若A为锐角,只有当????≥????????????????????时才有解,并且随着????的增大,得到的解的个数也不同;若A为钝角或直角,只有当????>????时才有解.
?
探究新知
三角形的解的个数
针对此类问题,我们有两种解决方法:
【1】正弦定理法(也称代数法或大边对大角法)
不妨设已知ΔABC的两边????,????和角A,根据正弦定理得????????????????????=????????????????????,可得????????????????=?????????????????????????.
?
①若????????????????>1,则三角形无解;
?
②若????????????????=1,则三角形有且仅有一个解;
?
③若0 大角),再求出B,从而确定三角形解的个数.
?
探究新知
三角形的解的个数
【2】公式法
不妨设已知ΔABC的两边????,????和角A,根据前面的分析可得三角形解的个数
的判断公式如下表:
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
?????
????≥????????°
?
????≥????
?
?????
??????????????????????
????=?????????????????????
?
?????
????>????
?
????≤????
?
一解
一解
两解
无解
一解
无解
探究新知
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
