6.4.2 余弦定理-课件(共17张PPT)
文档属性
| 名称 | 6.4.2 余弦定理-课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 21:24:02 | ||
图片预览






文档简介
第6章 平面向量及其应用
6.4.2 余弦定理
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
高中数学人教A版(2019)必修 第二册
余弦定理
余弦定理的描述
三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的乘积的两倍.符号语言:在ΔABC中,三个角A、B、C所对的边分别是????,????,????,则有
?
????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
适用范围:任意的三角形
结构特征:“平方”“乘积”“夹角”“余弦”
简单应用:等式中的三个边和一个角,四个元素可以做到“知三求一”
探究新知
余弦定理
余弦定理的应用
已知三角形的三边,求三角形的三个内角
——考什么
已知三角形的两边及一个角,求其他边和角
——怎么考
作为知识形态,放在选择题,填空题中考
作为工具形态,和其他知识点比如不等式、
向量结合考
勾股定理与余弦定理的联系:
勾股定理指出了直角三角形中三边平方之间的关系,余弦定理则指出了一般三角形中三边平方与其中一个角之间的关系,因此勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【1】向量法
????
?
????
?
????
?
从而????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
如图,因为AC=AB+AC,
所以AC2=(AB+BC)2,即
AC2=AB2+BC2+2AB · BC=AB2+BC2+2|AB||BC|(cos180°-B)
同理,根据AB=AC+CB,BC=BA+AC,可以得到
????
?
????
?
????
?
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
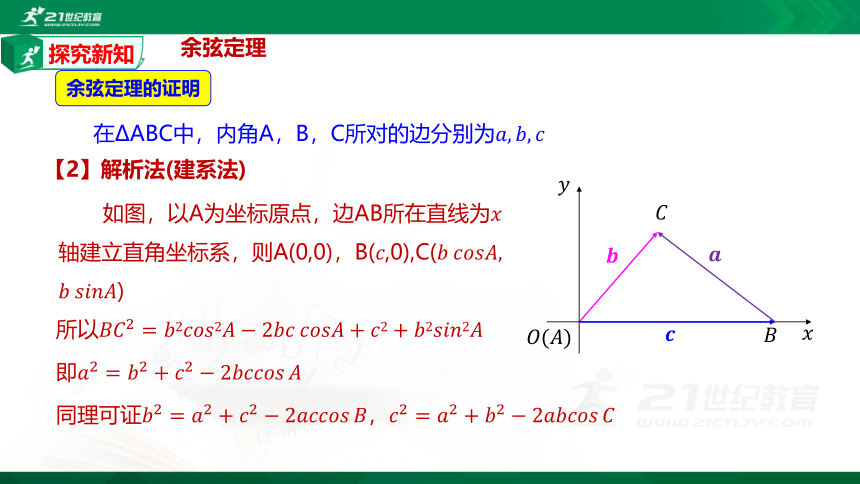
【2】解析法(建系法)
????
?
????
?
????
?
如图,以A为坐标原点,边AB所在直线为????轴建立直角坐标系,则A(0,0),B(????,0),C(?????????????????????,
?????????????????????)
?
????
?
????
?
????(????)
?
????
?
????
?
所以????????2=????2????????????2?????2?????????????????????????+????2+????2????????????2????
?
即????2=????2+????2?2????????????????????????
?
同理可证????2=????2+????2?2????????????????????????,????2=????2+????2?2????????????????????????
?
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【3】几何法
????
?
????
?
????
?
①当ΔABC为锐角三角形时,如图,过顶点C作
CD⊥AB于点D,则????????=?????????????????????,????????=?????????????????????,
???????????=?????????????????=??????????????????????????.
?
????
?
????
?
??
?
????
?
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,
即????2=????2????????????2????+??????????????????????????2=????2????????????2????+????2+????2????????????2?????2?????????????????????????
=????2+????2?2????????????????????????, 所以????2=????2+????2?2????????????????????????
?
同理可证????2=????2+????2?2????????????????????????,????2=????2+????2?2????????????????????????
?
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【3】几何法
????
?
????
?
????
?
②当ΔABC为直角三角形时,同理可证.
????
?
????
?
????
?
????
?
③当ΔABC为钝角三角形时,如图,过顶点C作CD⊥AB,交AB的延长线与点D,
则????????=?????????????????????,????????=?????????????????????,????????=??????????????????????????.
?
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,即
????2=????2????????????2????+??????????????????????????2, 即????2=????2+????2?2????????????????????????
?
同理可证????2=????2+????2?2????????????????????????,????2=????2+????2?2????????????????????????
?
探究新知
余弦定理
余弦定理的应用
用余弦定理判断三角形的类型:
①如果????2+????2=????2,那么角????是直角;
?
由此可知,余弦定理是用准确的量化关系去解决问题,即用边长去判断三角形的形状.
②如果????2+????2?
③如果????2+????2>????2,那么角????是锐角.
?
在ΔABC中,等式AC=AB+BC两边同乘AC,可得AC2=AB·AC+BC·AC
即得????2=????·?????????????????????+????·?????????????????????,所以????=????·????????????????+????·????????????????
?
同理有 ????=????·????????????????+????·????????????????
?
????=????·????????????????+????·????????????????
?
可用来判断三角形形状,求长度等等
探究新知
余弦定理
余弦定理的推论
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
其他常用的形式还有——
★????=????????°?????????=????????+?????????????????
?
★????=????????????°?????????=????????+????????+????????
?
★????=????????°?????????=????????+?????????????????????
?
★????=????????????°?????????=????????+????????+????????????
?
★????=????????°?????????=????????+?????????????????????
?
★????=????????????°?????????=????????+????????+????????????
?
探究新知
解三角形
解三角形
一般地,三角形的三个角A,B,C和它们的对边叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.
1
2
【1】已知三角形的三边解三角形
余弦定理在解三角形中的应用
①连续用余弦定理求出两角
②由三角形内角和定理求出第三个角
【2】已知两边和它们的夹角解三角形
①用余弦定理求出第三边
②用余弦定理求出第二个角
③由三角形内角和定理求出第三个角
探究新知
忽视三角形的构成条件——两边之和大于第三边.
忽略构成三角形的条件
已知钝角三角形ABC的三边????=????,????=????+2,????=????+4,求实数????的范围.
?
【错解】∵????>????>????,且ΔABC为钝角三角形,∴C为钝角
?
由余弦定理的推论得?????????????????=????2+????2?????22????????=????2?4?????122????(????+2)<0
?
∴ ?????????4?????12<0,解得?2?
又 ∵ ????为三角形的边长,所以0?
【正解】∵????>????>????,且ΔABC为钝角三角形,∴C为钝角
?
由余弦定理的推论得?????????????????=????2+????2?????22????????=????2?4?????122????(????+2)<0
?
∴ ?????????4?????12<0,解得?2?
由三角形两边之和大于第三边得????+????+2>????+4,解得????>2,∴ ????∈(2,6)
?
在ΔABC中,内角A,B,C的对边分别为?????,????,????,且????2=????2?????2+2????????,则角B的大小是多少?
?
题①
【解】由已知得????2+????2?????2=2????????,∴????????????????=????2+????2?????22????????=22
?
又∵0<B<180°,所以B=45°
在ΔABC中,若?????
题②
【解】∵ ????20
?
∴∠C为锐角,∵ ?????
∴ΔABC为锐角三角形
针对练习
在ΔABC中,内角A,B,C所对的边分别是?????,????,?????,且????=1,????=????=2,求????????????????的大小.
?
题③
——已知三边解三角形
【解】因为????=1,????=????=2?,
?
由余弦定理????????????????=????????+?????????????????????????????
?
可得????????????????=12+22?222×1×2=14
?
根据余弦定理的推论可知,只要将三角形三边的长度或者三边长度的比值求出,就可以求出三个角的余弦值,从而求出三个角的大小.
针对练习
在ΔABC中,内角A,B,C所对的边分别是?????,????,?????,且????=2,????=22,????=15°,求????,????和????.
?
题④
——已知两边及一角解三角形
【解】由余弦定理可得????????=????2+????2?????????????????????????????
?
即????????=4+8?2×2×22×????????????15°=12?82×????????????15°
?
∵ ????????????15°=cos45°?30°=????????????45°????????????30°+????????????45°????????????30°=6+24
?
∴ ????????=?????????12=6?22, ∴ ????=6?2或?(6?2)(舍)
?
∵ ????????????????=????????+?????????????????????????????=32,且0<A<180°,∴A=30°,B=180°-(A+C)=135°
?
∴ A=30°,B=135°, ????=6?2
?
针对练习
在ΔABC中,内角A,B,C所对的边分别是?????,????,?????,且????+????+????????+?????????=3????????,????????????????=2????????????????????????????????,?判断ΔABC的形状.
?
题⑤
——判断三角形的形状
【解】因为????+????+????????+?????????=3????????,化简得????2=????2+????2?????????
?
由余弦定理得????2=????2+????2?2?????????????????????????,所以????????????????=12
?
又因为0<A<180°,所以A=60°
因为????????????????=????????????????+????=????????????????????????????????+????????????????????????????????,且????????????????=2????????????????????????????????
?
所以????????????????????????????????=????????????????????????????????,所以B-C=0°,即B=C
?
又因为A=60°,所以ΔABC为等边三角形.
针对练习
谢谢聆听
6.4.2 余弦定理
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
高中数学人教A版(2019)必修 第二册
余弦定理
余弦定理的描述
三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的乘积的两倍.符号语言:在ΔABC中,三个角A、B、C所对的边分别是????,????,????,则有
?
????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
适用范围:任意的三角形
结构特征:“平方”“乘积”“夹角”“余弦”
简单应用:等式中的三个边和一个角,四个元素可以做到“知三求一”
探究新知
余弦定理
余弦定理的应用
已知三角形的三边,求三角形的三个内角
——考什么
已知三角形的两边及一个角,求其他边和角
——怎么考
作为知识形态,放在选择题,填空题中考
作为工具形态,和其他知识点比如不等式、
向量结合考
勾股定理与余弦定理的联系:
勾股定理指出了直角三角形中三边平方之间的关系,余弦定理则指出了一般三角形中三边平方与其中一个角之间的关系,因此勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【1】向量法
????
?
????
?
????
?
从而????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
????2=????2+????2?2????????????????????????
?
如图,因为AC=AB+AC,
所以AC2=(AB+BC)2,即
AC2=AB2+BC2+2AB · BC=AB2+BC2+2|AB||BC|(cos180°-B)
同理,根据AB=AC+CB,BC=BA+AC,可以得到
????
?
????
?
????
?
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【2】解析法(建系法)
????
?
????
?
????
?
如图,以A为坐标原点,边AB所在直线为????轴建立直角坐标系,则A(0,0),B(????,0),C(?????????????????????,
?????????????????????)
?
????
?
????
?
????(????)
?
????
?
????
?
所以????????2=????2????????????2?????2?????????????????????????+????2+????2????????????2????
?
即????2=????2+????2?2????????????????????????
?
同理可证????2=????2+????2?2????????????????????????,????2=????2+????2?2????????????????????????
?
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【3】几何法
????
?
????
?
????
?
①当ΔABC为锐角三角形时,如图,过顶点C作
CD⊥AB于点D,则????????=?????????????????????,????????=?????????????????????,
???????????=?????????????????=??????????????????????????.
?
????
?
????
?
??
?
????
?
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,
即????2=????2????????????2????+??????????????????????????2=????2????????????2????+????2+????2????????????2?????2?????????????????????????
=????2+????2?2????????????????????????, 所以????2=????2+????2?2????????????????????????
?
同理可证????2=????2+????2?2????????????????????????,????2=????2+????2?2????????????????????????
?
探究新知
余弦定理
余弦定理的证明
在ΔABC中,内角A,B,C所对的边分别为????,????,????
?
【3】几何法
????
?
????
?
????
?
②当ΔABC为直角三角形时,同理可证.
????
?
????
?
????
?
????
?
③当ΔABC为钝角三角形时,如图,过顶点C作CD⊥AB,交AB的延长线与点D,
则????????=?????????????????????,????????=?????????????????????,????????=??????????????????????????.
?
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,即
????2=????2????????????2????+??????????????????????????2, 即????2=????2+????2?2????????????????????????
?
同理可证????2=????2+????2?2????????????????????????,????2=????2+????2?2????????????????????????
?
探究新知
余弦定理
余弦定理的应用
用余弦定理判断三角形的类型:
①如果????2+????2=????2,那么角????是直角;
?
由此可知,余弦定理是用准确的量化关系去解决问题,即用边长去判断三角形的形状.
②如果????2+????2?
③如果????2+????2>????2,那么角????是锐角.
?
在ΔABC中,等式AC=AB+BC两边同乘AC,可得AC2=AB·AC+BC·AC
即得????2=????·?????????????????????+????·?????????????????????,所以????=????·????????????????+????·????????????????
?
同理有 ????=????·????????????????+????·????????????????
?
????=????·????????????????+????·????????????????
?
可用来判断三角形形状,求长度等等
探究新知
余弦定理
余弦定理的推论
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????????????=????????+?????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
????????+?????????????????=????????????????????????????
?
其他常用的形式还有——
★????=????????°?????????=????????+?????????????????
?
★????=????????????°?????????=????????+????????+????????
?
★????=????????°?????????=????????+?????????????????????
?
★????=????????????°?????????=????????+????????+????????????
?
★????=????????°?????????=????????+?????????????????????
?
★????=????????????°?????????=????????+????????+????????????
?
探究新知
解三角形
解三角形
一般地,三角形的三个角A,B,C和它们的对边叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.
1
2
【1】已知三角形的三边解三角形
余弦定理在解三角形中的应用
①连续用余弦定理求出两角
②由三角形内角和定理求出第三个角
【2】已知两边和它们的夹角解三角形
①用余弦定理求出第三边
②用余弦定理求出第二个角
③由三角形内角和定理求出第三个角
探究新知
忽视三角形的构成条件——两边之和大于第三边.
忽略构成三角形的条件
已知钝角三角形ABC的三边????=????,????=????+2,????=????+4,求实数????的范围.
?
【错解】∵????>????>????,且ΔABC为钝角三角形,∴C为钝角
?
由余弦定理的推论得?????????????????=????2+????2?????22????????=????2?4?????122????(????+2)<0
?
∴ ?????????4?????12<0,解得?2?
又 ∵ ????为三角形的边长,所以0?
【正解】∵????>????>????,且ΔABC为钝角三角形,∴C为钝角
?
由余弦定理的推论得?????????????????=????2+????2?????22????????=????2?4?????122????(????+2)<0
?
∴ ?????????4?????12<0,解得?2?
由三角形两边之和大于第三边得????+????+2>????+4,解得????>2,∴ ????∈(2,6)
?
在ΔABC中,内角A,B,C的对边分别为?????,????,????,且????2=????2?????2+2????????,则角B的大小是多少?
?
题①
【解】由已知得????2+????2?????2=2????????,∴????????????????=????2+????2?????22????????=22
?
又∵0<B<180°,所以B=45°
在ΔABC中,若?????
题②
【解】∵ ????20
?
∴∠C为锐角,∵ ?????
∴ΔABC为锐角三角形
针对练习
在ΔABC中,内角A,B,C所对的边分别是?????,????,?????,且????=1,????=????=2,求????????????????的大小.
?
题③
——已知三边解三角形
【解】因为????=1,????=????=2?,
?
由余弦定理????????????????=????????+?????????????????????????????
?
可得????????????????=12+22?222×1×2=14
?
根据余弦定理的推论可知,只要将三角形三边的长度或者三边长度的比值求出,就可以求出三个角的余弦值,从而求出三个角的大小.
针对练习
在ΔABC中,内角A,B,C所对的边分别是?????,????,?????,且????=2,????=22,????=15°,求????,????和????.
?
题④
——已知两边及一角解三角形
【解】由余弦定理可得????????=????2+????2?????????????????????????????
?
即????????=4+8?2×2×22×????????????15°=12?82×????????????15°
?
∵ ????????????15°=cos45°?30°=????????????45°????????????30°+????????????45°????????????30°=6+24
?
∴ ????????=?????????12=6?22, ∴ ????=6?2或?(6?2)(舍)
?
∵ ????????????????=????????+?????????????????????????????=32,且0<A<180°,∴A=30°,B=180°-(A+C)=135°
?
∴ A=30°,B=135°, ????=6?2
?
针对练习
在ΔABC中,内角A,B,C所对的边分别是?????,????,?????,且????+????+????????+?????????=3????????,????????????????=2????????????????????????????????,?判断ΔABC的形状.
?
题⑤
——判断三角形的形状
【解】因为????+????+????????+?????????=3????????,化简得????2=????2+????2?????????
?
由余弦定理得????2=????2+????2?2?????????????????????????,所以????????????????=12
?
又因为0<A<180°,所以A=60°
因为????????????????=????????????????+????=????????????????????????????????+????????????????????????????????,且????????????????=2????????????????????????????????
?
所以????????????????????????????????=????????????????????????????????,所以B-C=0°,即B=C
?
又因为A=60°,所以ΔABC为等边三角形.
针对练习
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
