6.4.4 正弦定理、余弦定理应用举例课件(共18张PPT)
文档属性
| 名称 | 6.4.4 正弦定理、余弦定理应用举例课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 20:17:50 | ||
图片预览



文档简介
第6章 平面向量及其应用
6.4.4 正弦定理、余弦定理应用举例
铅
垂
线
视线
视线
水平线
仰角
俯角
北
东
????
?
????????????°
?
北
东
????
?
????????°
?
????
?
????????°
?
????
?
高中数学人教A版(2019)必修 第二册
测量距离问题
知识概要
解三角形的知识在测量、航海、几何、物理学中都有非常广泛的应用,如果我们抽去每个应用题中与生活生产实际联系的外壳, 就暴露出解三角形的问题的本质,这就要求我们要提高分析问题和解决问题的能力以及化实际问题为抽象的数学问题的技巧和能力.
在测量上,我们根据测量需要,适当确定的线段叫做基线,一般来说,基线越长,测量的精确度就越高.
在与实际结合的应用题中常常会出现一些测量专有概念,需要我们掌握,以下是常见的几个概念:
探究新知
测量距离问题
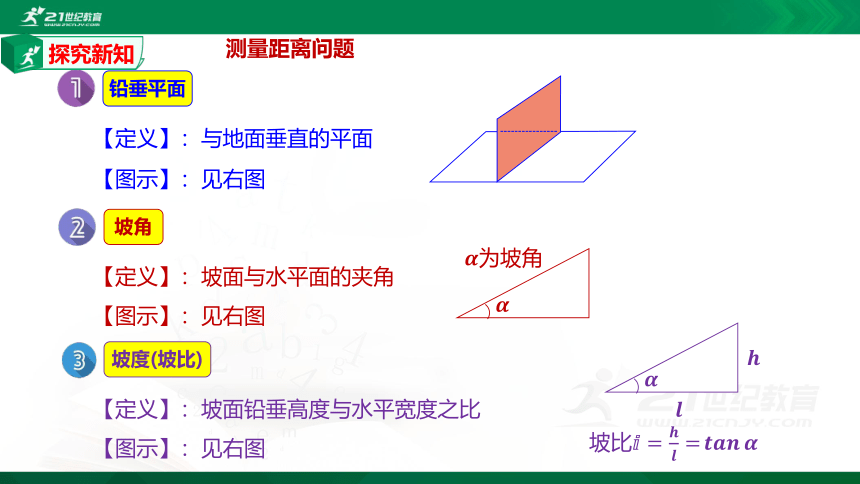
铅垂平面
【定义】:与地面垂直的平面
【图示】:见右图
坡角
【定义】:坡面与水平面的夹角
【图示】:见右图
????
?
????为坡角
?
坡度(坡比)
【定义】:坡面铅垂高度与水平宽度之比
【图示】:见右图
????
?
坡比?=????????=????????????????
?
????
?
????
?
探究新知
测量距离问题
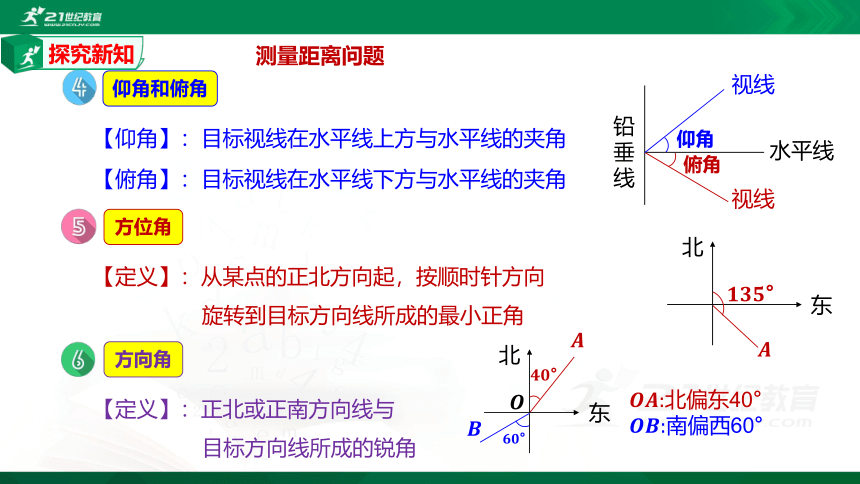
仰角和俯角
【仰角】:目标视线在水平线上方与水平线的夹角
【俯角】:目标视线在水平线下方与水平线的夹角
方位角
【定义】:从某点的正北方向起,按顺时针方向
旋转到目标方向线所成的最小正角
铅
垂
线
方向角
【定义】:正北或正南方向线与
目标方向线所成的锐角
视线
视线
水平线
仰角
俯角
北
东
????
?
????????????°
?
北
东
????
?
????????°
?
????
?
????????°
?
????
?
????????:北偏东40°
????????:南偏西60°
?
探究新知
测量距离问题
题型【1】
——不相通的两点间的距离
????
?
????
?
????
?
????
?
????
?
????
?
【解法】:先选定适当的位置C,用测角器测出∠ACB即????的大小,再分别测出
AC,BC的长度,则可求出AB之间的距离,即
????????=????????+?????????????????????????????????????
?
探究新知
测量距离问题
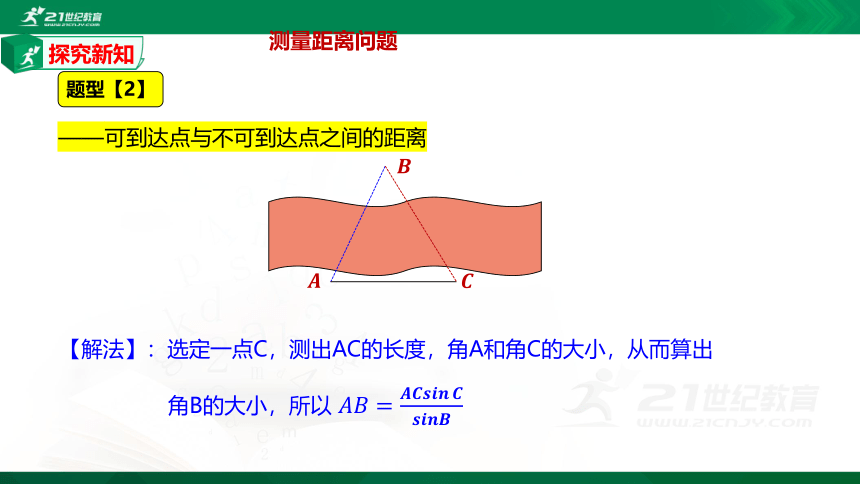
题型【2】
——可到达点与不可到达点之间的距离
【解法】:选定一点C,测出AC的长度,角A和角C的大小,从而算出
角B的大小,所以 ????????=????????????????????????????????????????
?
????
?
????
?
????
?
探究新知
测量距离问题
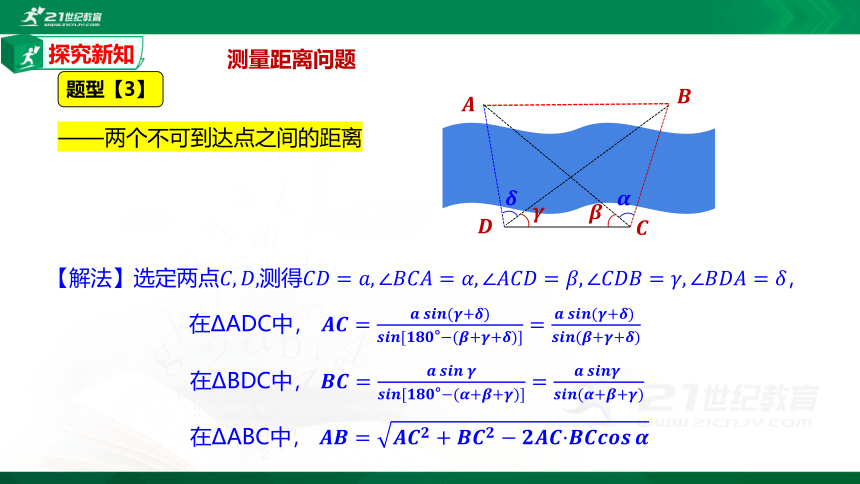
题型【3】
——两个不可到达点之间的距离
【解法】选定两点????,????,测得????????=????,∠????????????=????,∠????????????=????,∠????????????=????,∠????????????=????,
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
在ΔADC中, ????????=??????????????????(????+????)????????????[????????????°?(????+????+????)]=?????????????????(????+????)?????????????(????+????+????)
?
在ΔBDC中, ????????=??????????????????????????????????[????????????°?(????+????+????)]=??????????????????????????????????(????+????+????)
?
在ΔABC中, ????????=????????????+?????????????????????????·????????????????????????
?
探究新知
测量高度问题
题型【1】
——底部可达
????
?
????
?
????
?
????
?
【解法】:测出????的长度,角C的大小,解直角三角形,得
?
????????=?????????????????????
?
探究新知
测量高度问题
题型【2】
——底部不可达(B与C,D共线)
????
?
????
?
????
?
【解法】:测得CD及角,∠ADC的度数,先用正弦定理求出AC(或AD),
再解直角三角形ABC(或RtΔABD),求出AB的长度
????
?
????
?
探究新知
测量高度问题
题型【2】
——底部不可达(B与C,D不共线)
????
?
????
?
????
?
【解法】:测得CD及角,∠BCD,∠BDC,∠ACB的度数,在ΔBCD中由
正弦定理求得BC,再解ΔABC求得AB的长度.
????
?
????
?
探究新知
测量角度问题
测量角度问题主要指的是在海上或空中.如:确定目标的方位,观察某一建筑的视角等问题,解题的关键是根据题意和图形及有关概念抽象出一个或几个三角形,确定所求角在哪个三角形中,分析三角形中有哪些是已知量,需要求哪些量,然后通过解三角形得到所求的量,进而得到实际问题的解.解题时应认真审题,结合图形选择相关定理,这是最重要的一步.
考
什
么
①作为测量问题,重点考察长度,距离,高度,角度等问题
①正弦定理和余弦定理的实际测量问题的应用难度降低,命题形式一般为填空题
②作为平面几何问题,重点考察解三角形或者求三角形面积问题
怎
么
考
②三角形的面积公式成为高考考察的高频考点,试题会牵涉到三角函数的图像与性质,三角恒等变换及基本不等式等等.
探究新知
如图,在公园内有一块边长为2????的等边三角形空地(记为ΔABC),现在修成草坪,图中DE把草坪分成面积相等的两个部分,点D在AB上,点E在AC上.设AD= ????(????≥????),DE= ????,求 ?????与??????之间的函数关系式.
?
题①
【解】根据题意有????≤????≤2????,
?
????
?
????
?
????
?
????
?
????
?
∵ ????????????????????=????????????????????????????=????????????????=????????????·????????·????????????????????°,
?
∴ ????????=????????????????,在ΔADE中,由余弦定理,得????????=????????+?????????????????????????????·????????????????·????????????????????°,
?
∴ ????=????????+?????????????????????????????????(????≤????≤????????)
?
针对训练
如图,某货轮在A处看灯塔B位于北偏东75°方向,距离为126海里,在A处看灯塔C位于北偏西30°方向,距离为83海里,货轮由A处向正北方向航行到D处时,再看灯塔B位于南偏东60°方向,求AD之间的距离.
?
题②
【解】在ΔABD中,∠ADB=60°,∠DAB=75°,
????
?
????
?
????
?
????
?
????????°
?
——测量距离问题
????????°
?
????????°
?
∴∠B=180°-60°-75°=45°
又 ∵AB= 126海里,由正弦定理可得????????=????????????????????????????????????∠????????????=????????????×????????????????=????????海里
?
即AD之间的距离为24海里
针对训练
在福州青运会开幕式举行的升旗仪式上,从坡角为15°的看台上,同一列的第一排和最后一排分别测得旗杆顶部的仰角为60°和30°.若同一列的第一排和最后一排之间的距离是106米(如图),求旗杆的高度.
?
题③
【解】如图,记看台上的一列为BC,旗杆为OP,
——测量高度问题
最后一排
看台
第一排
旗杆
????????°
?
????????°
?
????????°
?
????????????米
?
????
?
????
?
????
?
????
?
由题意有∠PCB=45°,∠PBC=180°-60°-15°=105°,∠PBO=60°,BC=106米
?
在ΔPBC中,由正弦定理可知????????=????????????????????∠????????????·????????????∠????????????=????????????(米)
?
在RtΔPOB中,由正弦定理可知????????=????????·????????????∠????????????=????????????·????????=????????(米)
?
针对训练
宜秀区准备建造一座主题游戏园,该游戏园为四边形区域ABCD,其中三角形区域ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=126m,AD,CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD,CD围成的三角形区域ADC为游客休闲中心,求AC的长度.
?
题④
【解】在ΔABC中,由正弦定理得????????????????????∠????????????=????????????????????∠????????????,
?
????
?
????
?
????
?
????
?
又∠ACB=60°,∠ABC=45°,AB=126?m,
?
所以????????=????????????????????????????????°????????????????????°=24?????
?
针对训练
【课标全国Ⅰ文2018·16】ΔABC的内角A,B,C的对边分别为????,????,????,已知
?????????????????????+?????????????????????=4??????????????????????????????????????,????2+????2?????2=8,求ΔABC的面积
?
题⑤
【解】由正弦定理知?????????????????????+?????????????????????=??????????????????????????可转化为
?
?????????????????????????????????+?????????????????????????????????=??????????????????????????????????????????????????????
?
∵ ?????????????????????????????????≠????,∴ ????????????????=????????
?
∵ ????????+?????????????????=????,?????????????????????????????=????,则A为锐角
?
∴ ????????????????=????????,则????????=????????
?
∴ ????????????????????=?????????????????????????????????=????????×????????×????????=????????????
?
针对训练
谢谢聆听
6.4.4 正弦定理、余弦定理应用举例
铅
垂
线
视线
视线
水平线
仰角
俯角
北
东
????
?
????????????°
?
北
东
????
?
????????°
?
????
?
????????°
?
????
?
高中数学人教A版(2019)必修 第二册
测量距离问题
知识概要
解三角形的知识在测量、航海、几何、物理学中都有非常广泛的应用,如果我们抽去每个应用题中与生活生产实际联系的外壳, 就暴露出解三角形的问题的本质,这就要求我们要提高分析问题和解决问题的能力以及化实际问题为抽象的数学问题的技巧和能力.
在测量上,我们根据测量需要,适当确定的线段叫做基线,一般来说,基线越长,测量的精确度就越高.
在与实际结合的应用题中常常会出现一些测量专有概念,需要我们掌握,以下是常见的几个概念:
探究新知
测量距离问题
铅垂平面
【定义】:与地面垂直的平面
【图示】:见右图
坡角
【定义】:坡面与水平面的夹角
【图示】:见右图
????
?
????为坡角
?
坡度(坡比)
【定义】:坡面铅垂高度与水平宽度之比
【图示】:见右图
????
?
坡比?=????????=????????????????
?
????
?
????
?
探究新知
测量距离问题
仰角和俯角
【仰角】:目标视线在水平线上方与水平线的夹角
【俯角】:目标视线在水平线下方与水平线的夹角
方位角
【定义】:从某点的正北方向起,按顺时针方向
旋转到目标方向线所成的最小正角
铅
垂
线
方向角
【定义】:正北或正南方向线与
目标方向线所成的锐角
视线
视线
水平线
仰角
俯角
北
东
????
?
????????????°
?
北
东
????
?
????????°
?
????
?
????????°
?
????
?
????????:北偏东40°
????????:南偏西60°
?
探究新知
测量距离问题
题型【1】
——不相通的两点间的距离
????
?
????
?
????
?
????
?
????
?
????
?
【解法】:先选定适当的位置C,用测角器测出∠ACB即????的大小,再分别测出
AC,BC的长度,则可求出AB之间的距离,即
????????=????????+?????????????????????????????????????
?
探究新知
测量距离问题
题型【2】
——可到达点与不可到达点之间的距离
【解法】:选定一点C,测出AC的长度,角A和角C的大小,从而算出
角B的大小,所以 ????????=????????????????????????????????????????
?
????
?
????
?
????
?
探究新知
测量距离问题
题型【3】
——两个不可到达点之间的距离
【解法】选定两点????,????,测得????????=????,∠????????????=????,∠????????????=????,∠????????????=????,∠????????????=????,
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
在ΔADC中, ????????=??????????????????(????+????)????????????[????????????°?(????+????+????)]=?????????????????(????+????)?????????????(????+????+????)
?
在ΔBDC中, ????????=??????????????????????????????????[????????????°?(????+????+????)]=??????????????????????????????????(????+????+????)
?
在ΔABC中, ????????=????????????+?????????????????????????·????????????????????????
?
探究新知
测量高度问题
题型【1】
——底部可达
????
?
????
?
????
?
????
?
【解法】:测出????的长度,角C的大小,解直角三角形,得
?
????????=?????????????????????
?
探究新知
测量高度问题
题型【2】
——底部不可达(B与C,D共线)
????
?
????
?
????
?
【解法】:测得CD及角,∠ADC的度数,先用正弦定理求出AC(或AD),
再解直角三角形ABC(或RtΔABD),求出AB的长度
????
?
????
?
探究新知
测量高度问题
题型【2】
——底部不可达(B与C,D不共线)
????
?
????
?
????
?
【解法】:测得CD及角,∠BCD,∠BDC,∠ACB的度数,在ΔBCD中由
正弦定理求得BC,再解ΔABC求得AB的长度.
????
?
????
?
探究新知
测量角度问题
测量角度问题主要指的是在海上或空中.如:确定目标的方位,观察某一建筑的视角等问题,解题的关键是根据题意和图形及有关概念抽象出一个或几个三角形,确定所求角在哪个三角形中,分析三角形中有哪些是已知量,需要求哪些量,然后通过解三角形得到所求的量,进而得到实际问题的解.解题时应认真审题,结合图形选择相关定理,这是最重要的一步.
考
什
么
①作为测量问题,重点考察长度,距离,高度,角度等问题
①正弦定理和余弦定理的实际测量问题的应用难度降低,命题形式一般为填空题
②作为平面几何问题,重点考察解三角形或者求三角形面积问题
怎
么
考
②三角形的面积公式成为高考考察的高频考点,试题会牵涉到三角函数的图像与性质,三角恒等变换及基本不等式等等.
探究新知
如图,在公园内有一块边长为2????的等边三角形空地(记为ΔABC),现在修成草坪,图中DE把草坪分成面积相等的两个部分,点D在AB上,点E在AC上.设AD= ????(????≥????),DE= ????,求 ?????与??????之间的函数关系式.
?
题①
【解】根据题意有????≤????≤2????,
?
????
?
????
?
????
?
????
?
????
?
∵ ????????????????????=????????????????????????????=????????????????=????????????·????????·????????????????????°,
?
∴ ????????=????????????????,在ΔADE中,由余弦定理,得????????=????????+?????????????????????????????·????????????????·????????????????????°,
?
∴ ????=????????+?????????????????????????????????(????≤????≤????????)
?
针对训练
如图,某货轮在A处看灯塔B位于北偏东75°方向,距离为126海里,在A处看灯塔C位于北偏西30°方向,距离为83海里,货轮由A处向正北方向航行到D处时,再看灯塔B位于南偏东60°方向,求AD之间的距离.
?
题②
【解】在ΔABD中,∠ADB=60°,∠DAB=75°,
????
?
????
?
????
?
????
?
????????°
?
——测量距离问题
????????°
?
????????°
?
∴∠B=180°-60°-75°=45°
又 ∵AB= 126海里,由正弦定理可得????????=????????????????????????????????????∠????????????=????????????×????????????????=????????海里
?
即AD之间的距离为24海里
针对训练
在福州青运会开幕式举行的升旗仪式上,从坡角为15°的看台上,同一列的第一排和最后一排分别测得旗杆顶部的仰角为60°和30°.若同一列的第一排和最后一排之间的距离是106米(如图),求旗杆的高度.
?
题③
【解】如图,记看台上的一列为BC,旗杆为OP,
——测量高度问题
最后一排
看台
第一排
旗杆
????????°
?
????????°
?
????????°
?
????????????米
?
????
?
????
?
????
?
????
?
由题意有∠PCB=45°,∠PBC=180°-60°-15°=105°,∠PBO=60°,BC=106米
?
在ΔPBC中,由正弦定理可知????????=????????????????????∠????????????·????????????∠????????????=????????????(米)
?
在RtΔPOB中,由正弦定理可知????????=????????·????????????∠????????????=????????????·????????=????????(米)
?
针对训练
宜秀区准备建造一座主题游戏园,该游戏园为四边形区域ABCD,其中三角形区域ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=126m,AD,CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD,CD围成的三角形区域ADC为游客休闲中心,求AC的长度.
?
题④
【解】在ΔABC中,由正弦定理得????????????????????∠????????????=????????????????????∠????????????,
?
????
?
????
?
????
?
????
?
又∠ACB=60°,∠ABC=45°,AB=126?m,
?
所以????????=????????????????????????????????°????????????????????°=24?????
?
针对训练
【课标全国Ⅰ文2018·16】ΔABC的内角A,B,C的对边分别为????,????,????,已知
?????????????????????+?????????????????????=4??????????????????????????????????????,????2+????2?????2=8,求ΔABC的面积
?
题⑤
【解】由正弦定理知?????????????????????+?????????????????????=??????????????????????????可转化为
?
?????????????????????????????????+?????????????????????????????????=??????????????????????????????????????????????????????
?
∵ ?????????????????????????????????≠????,∴ ????????????????=????????
?
∵ ????????+?????????????????=????,?????????????????????????????=????,则A为锐角
?
∴ ????????????????=????????,则????????=????????
?
∴ ????????????????????=?????????????????????????????????=????????×????????×????????=????????????
?
针对训练
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
