等腰三角形
图片预览


文档简介
(共25张PPT)
12.3.1等腰三角形
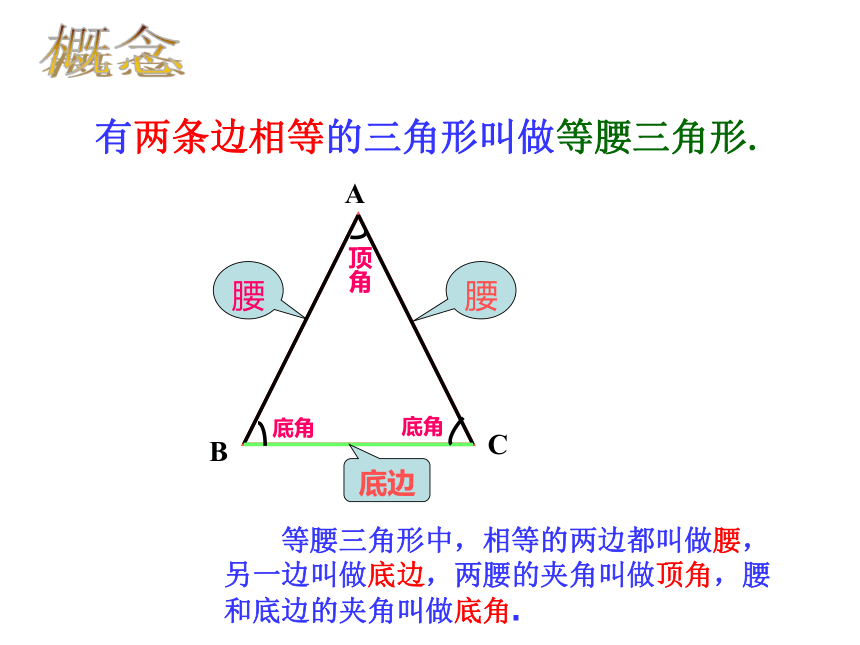
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
10 cm
10 cm 或 11 cm
19 cm
小试牛刀
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
※等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线。
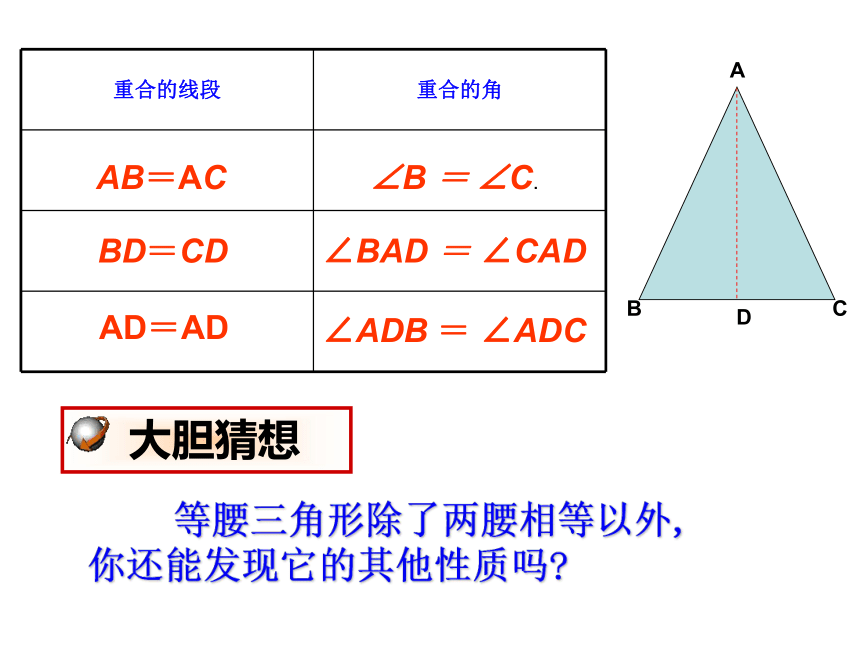
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗
大胆猜想
猜想与论证
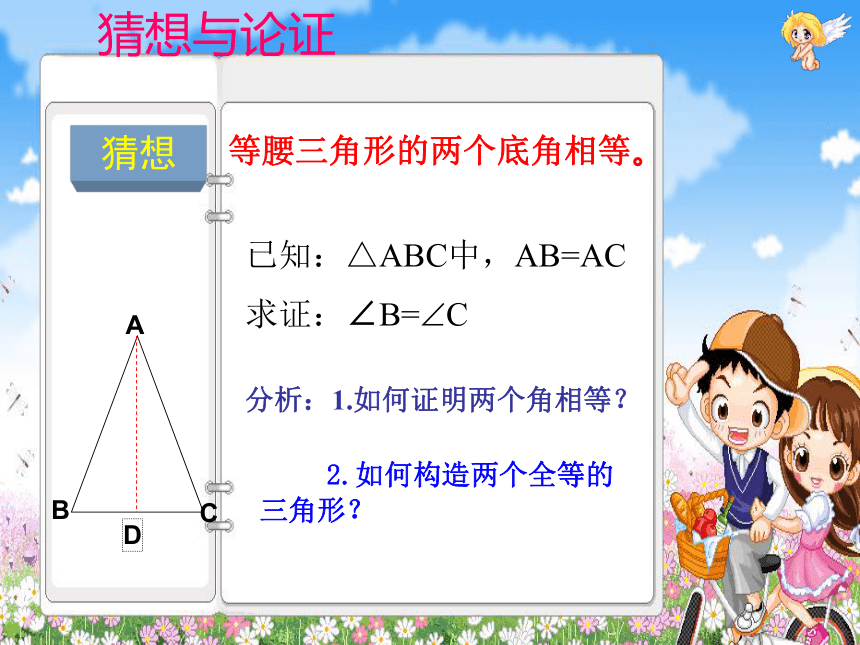
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
A
B
C
D
如何构造两个全等的三角形
A
B
C
A
B
C
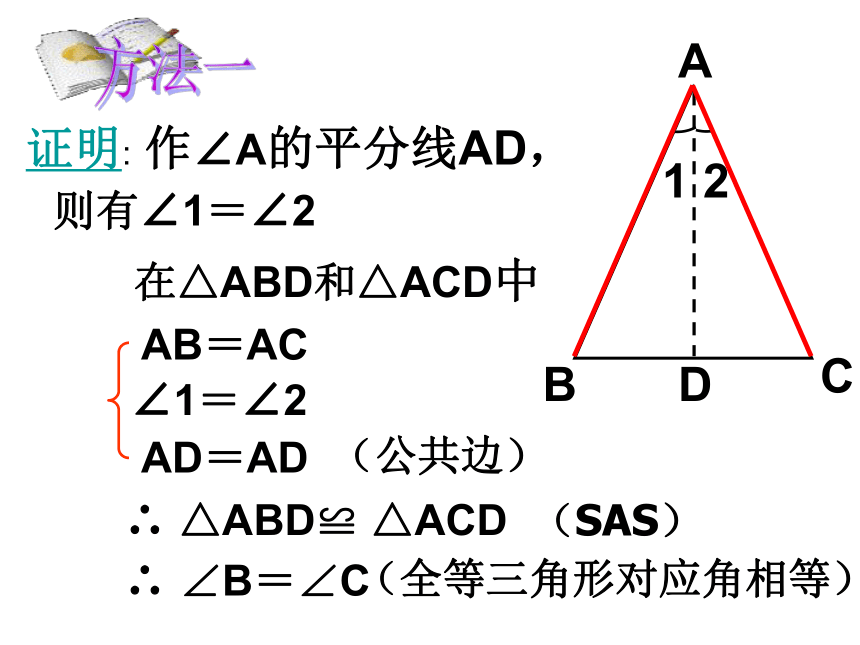
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作∠A的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
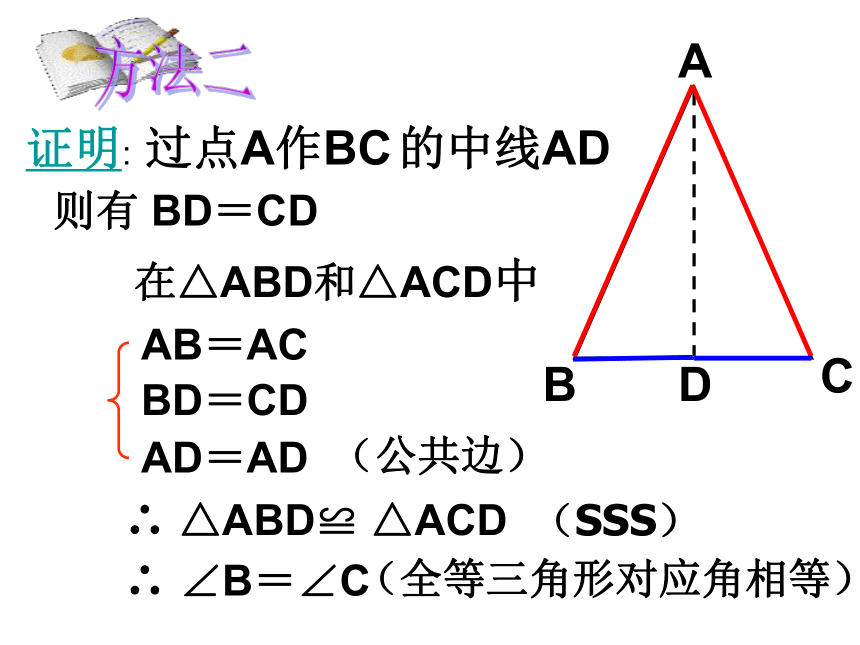
则有 BD=CD
D
在△ABD和△ACD中
证明: 过点A作BC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 过点A作AD⊥BC
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
等腰三角形的性质1:
等腰三角形的两个底角相等
简写成“等边对等角”
注意:
在 三角形中,等边对等角。
一个
一个
用符号语言表示为:
在△ABC中,
∵ AC=AB
∴ ∠B=∠C ( )
等边对等角
C
A
B
想一想:
刚才的证明除了能得到∠B=∠C 你还能发现什么
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
△ABC中,AB=AC, ∠BAD=∠CAD
△ABC中,AB=AC, BD=CD
∠BAD=∠CAD,
AD⊥BC
BD=CD ,
AD⊥BC
△ABC中,AB=AC,
(三)
AD⊥BC
BD=CD,
∠BAD=∠CAD
∴
∵
∴
∵
∴
∵
(一)
(二)
A
B
D
C
(等腰三角形的三线合一)
等腰三角形的顶角的平分线与底边上的中线,底边上的高互相重合
等腰三角形的性质2:
(1)如果等腰三角形的一个底角为500,则其余两个角为____和____.
(2)如果等腰三角形的顶角为800,则它的一个底角为____.
500
800
500
1.填空题
巩固练习
(3)如果等腰三角形的一个角为800,则其余两个角为___________________.
800和200
(4)如果等腰三角形的一个角为1000,则其余两个角为_________.
400和400
或500和500
(5)等腰三角形的一个外角为1300,则三个内角分别:_______________________________.
650、650、500
或500、500、800
2.判断下列语句是否正确.
(1)等腰三角形的角平分线、中线和高互相重合.( )
×
×
(3)等腰三角形的底角都是锐角( )
(2)有一个角是60°的等腰三角形,其它两个内
角也为60 ° ( )
(4)钝角三角形不可能是等腰三角形 . ( )
例1 已知:在△ABC中,AB = AC,点D在AC上,BD = BC = AD, 求△ABC 各角的度数.
讨论:
2.∠A与哪些角相等?
1.∠C与哪些角相等?
3.∠C与∠A是什么关系?
(∠3、 ∠ABC )
(∠1、 ∠2 )
(∠C=2 ∠A)
A
C
B
D
1
2
3
例1 已知:在△ABC中,AB = AC,点A在AC上,BD = BC = AD, 求△ABC 各角的度数.
A
C
B
D
x
○
2x
2x
⌒
⌒
⌒
2x
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,∠ABC=∠C=72°
如图,△ABC中,AB=AC, BD=CD ,DE⊥AB,DF⊥AC,垂足为E、F, 求证:DE=DF
证明∵ AB=AC, BD=CD
∴ AD平分∠BAC
又∵ DE⊥AB,DF⊥AC
∴ DE=DF
结论:等腰三角形底边上的中点到两腰的距离相等
练一练:
1、如图,点D、E在△ABC的边BC上,且AB=AC,AD=AE, 求证:BD=CE
A
B
C
D
E
F
证明:过点A作AF⊥BC
∵ AB=AC AF⊥BC
∴ BF=CF
∵ AD=AE AF⊥BC
∴ DF=EF
∴ BF-DF=CF-EF
(等腰三角形的顶角的平分线与底边上的中线,底边上的高
互相重合)
即 BD=CE
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高
互相重合,简称“等腰三角形的三线合一”
课堂检测
书本:P51
1--3
1、如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FG、GH……,添加的钢管长度都与OE相等,则∠MHA = °最多能添加这样的钢管 根。
E
G
O
F
H
M
A
B
2.如果等腰三角形的顶角为α,则一腰上
的高与底边的夹角为
α
3.Rt △ABC中, ∠C=90°,点M、N在AB上,
且AM=AC,BN=BC,则∠MCN=
45°
A
C
B
M
N
2.如果等腰三角形的顶角为α,则一腰上
的高与底边的夹角为
3.Rt △ABC中, ∠C=90°,
点M、N在AB上,且AM=AC,
BN=BC,则∠MCN=
α
45°
A
C
B
M
N
(第3题图)
1、(1)在等腰△ABC中,AB =5,AC = 6,则
△ABC的周长= .
(2)在等腰△ABC中,AB =3,AC = 8,则
△ABC的周长= .
2、(1)在等腰△ABC中,AB =AC, ∠A = 50°,
则∠B = ,∠C= .
用一用:
16或17
19
65°
65°
(2)在等腰△ABC中,AB =AC, ∠B = 50°,
则∠A = ,∠C= .
80°
50°
A
B
C
12.3.1等腰三角形
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
10 cm
10 cm 或 11 cm
19 cm
小试牛刀
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
※等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线。
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗
大胆猜想
猜想与论证
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
A
B
C
D
如何构造两个全等的三角形
A
B
C
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作∠A的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 过点A作BC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 过点A作AD⊥BC
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
等腰三角形的性质1:
等腰三角形的两个底角相等
简写成“等边对等角”
注意:
在 三角形中,等边对等角。
一个
一个
用符号语言表示为:
在△ABC中,
∵ AC=AB
∴ ∠B=∠C ( )
等边对等角
C
A
B
想一想:
刚才的证明除了能得到∠B=∠C 你还能发现什么
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
△ABC中,AB=AC, ∠BAD=∠CAD
△ABC中,AB=AC, BD=CD
∠BAD=∠CAD,
AD⊥BC
BD=CD ,
AD⊥BC
△ABC中,AB=AC,
(三)
AD⊥BC
BD=CD,
∠BAD=∠CAD
∴
∵
∴
∵
∴
∵
(一)
(二)
A
B
D
C
(等腰三角形的三线合一)
等腰三角形的顶角的平分线与底边上的中线,底边上的高互相重合
等腰三角形的性质2:
(1)如果等腰三角形的一个底角为500,则其余两个角为____和____.
(2)如果等腰三角形的顶角为800,则它的一个底角为____.
500
800
500
1.填空题
巩固练习
(3)如果等腰三角形的一个角为800,则其余两个角为___________________.
800和200
(4)如果等腰三角形的一个角为1000,则其余两个角为_________.
400和400
或500和500
(5)等腰三角形的一个外角为1300,则三个内角分别:_______________________________.
650、650、500
或500、500、800
2.判断下列语句是否正确.
(1)等腰三角形的角平分线、中线和高互相重合.( )
×
×
(3)等腰三角形的底角都是锐角( )
(2)有一个角是60°的等腰三角形,其它两个内
角也为60 ° ( )
(4)钝角三角形不可能是等腰三角形 . ( )
例1 已知:在△ABC中,AB = AC,点D在AC上,BD = BC = AD, 求△ABC 各角的度数.
讨论:
2.∠A与哪些角相等?
1.∠C与哪些角相等?
3.∠C与∠A是什么关系?
(∠3、 ∠ABC )
(∠1、 ∠2 )
(∠C=2 ∠A)
A
C
B
D
1
2
3
例1 已知:在△ABC中,AB = AC,点A在AC上,BD = BC = AD, 求△ABC 各角的度数.
A
C
B
D
x
○
2x
2x
⌒
⌒
⌒
2x
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,∠ABC=∠C=72°
如图,△ABC中,AB=AC, BD=CD ,DE⊥AB,DF⊥AC,垂足为E、F, 求证:DE=DF
证明∵ AB=AC, BD=CD
∴ AD平分∠BAC
又∵ DE⊥AB,DF⊥AC
∴ DE=DF
结论:等腰三角形底边上的中点到两腰的距离相等
练一练:
1、如图,点D、E在△ABC的边BC上,且AB=AC,AD=AE, 求证:BD=CE
A
B
C
D
E
F
证明:过点A作AF⊥BC
∵ AB=AC AF⊥BC
∴ BF=CF
∵ AD=AE AF⊥BC
∴ DF=EF
∴ BF-DF=CF-EF
(等腰三角形的顶角的平分线与底边上的中线,底边上的高
互相重合)
即 BD=CE
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高
互相重合,简称“等腰三角形的三线合一”
课堂检测
书本:P51
1--3
1、如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FG、GH……,添加的钢管长度都与OE相等,则∠MHA = °最多能添加这样的钢管 根。
E
G
O
F
H
M
A
B
2.如果等腰三角形的顶角为α,则一腰上
的高与底边的夹角为
α
3.Rt △ABC中, ∠C=90°,点M、N在AB上,
且AM=AC,BN=BC,则∠MCN=
45°
A
C
B
M
N
2.如果等腰三角形的顶角为α,则一腰上
的高与底边的夹角为
3.Rt △ABC中, ∠C=90°,
点M、N在AB上,且AM=AC,
BN=BC,则∠MCN=
α
45°
A
C
B
M
N
(第3题图)
1、(1)在等腰△ABC中,AB =5,AC = 6,则
△ABC的周长= .
(2)在等腰△ABC中,AB =3,AC = 8,则
△ABC的周长= .
2、(1)在等腰△ABC中,AB =AC, ∠A = 50°,
则∠B = ,∠C= .
用一用:
16或17
19
65°
65°
(2)在等腰△ABC中,AB =AC, ∠B = 50°,
则∠A = ,∠C= .
80°
50°
A
B
C
