人教A版高中数学必修二4.2.1-直线与圆的位置关系课件(共15张PPT)
文档属性
| 名称 | 人教A版高中数学必修二4.2.1-直线与圆的位置关系课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 370.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
4.2.1
直线与圆的位置关系
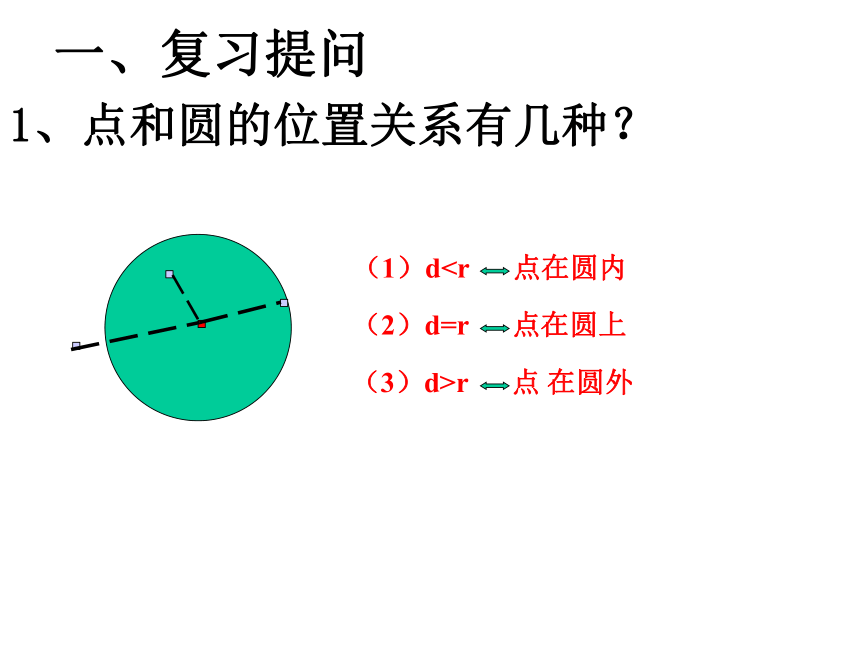
一、复习提问
1、点和圆的位置关系有几种?
(1)d点在圆内
(2)d=r
点在圆上
(3)d>r
点
在圆外
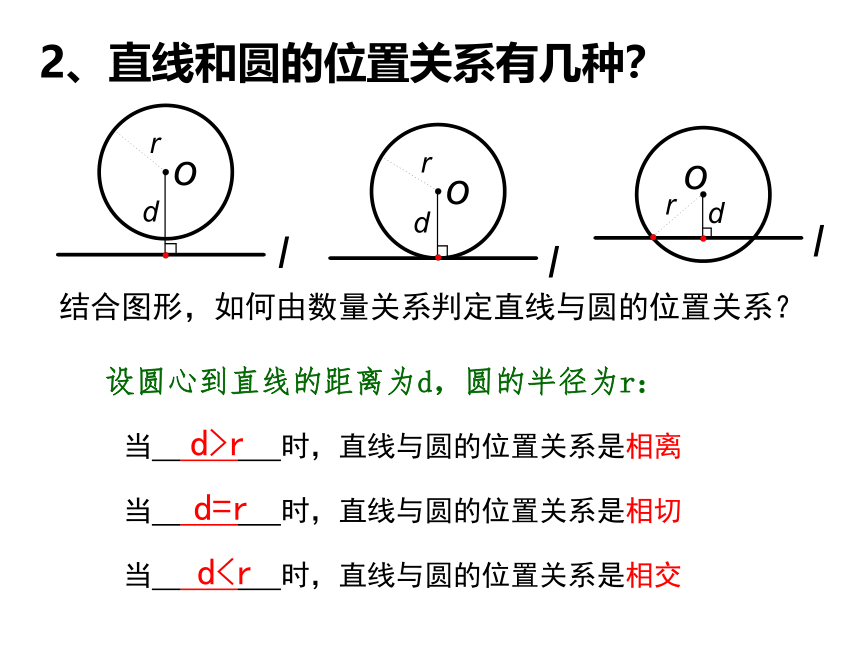
结合图形,如何由数量关系判定直线与圆的位置关系?
当
时,直线与圆的位置关系是相离
当
时,直线与圆的位置关系是相切
当
时,直线与圆的位置关系是相交
d>r
d=r
d设圆心到直线的距离为d,圆的半径为r:
2、直线和圆的位置关系有几种?
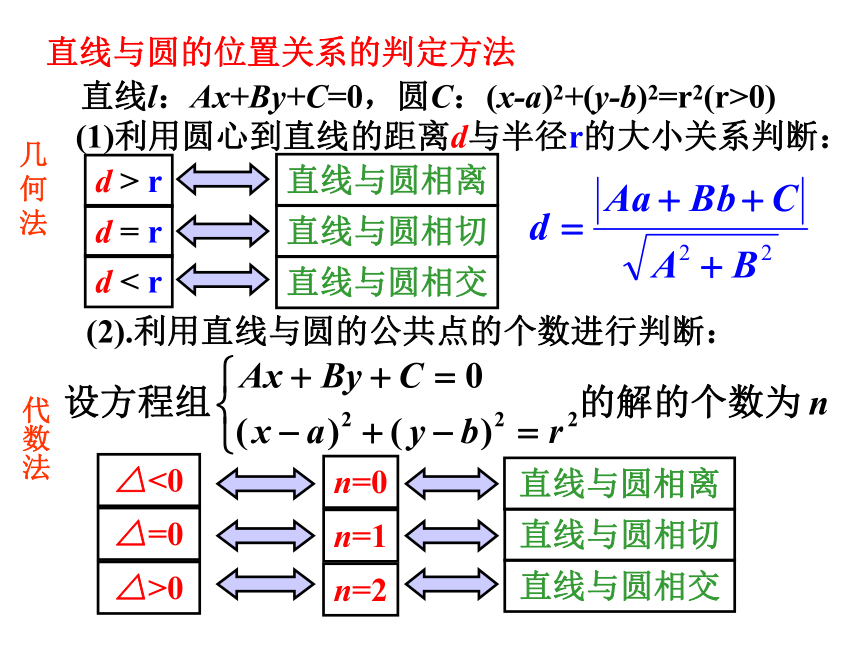
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法
d
>
r
d
=
r
d
<
r
直线与圆相离
直线与圆相切
直线与圆相交
(2).利用直线与圆的公共点的个数进行判断:
直线与圆相离
n=0
△<0
直线与圆相切
n=1
△=0
直线与圆相交
n=2
△>0
直线l:Ax+By+C=0,圆C:(x-a)2+(y-b)2=r2(r>0)
几何法
代数法
判断下列直线与圆的位置关系
相交
相切
相离
题型一:判断直线与圆的位置关系
解法一:
题型一:判断直线与圆的位置关系
解法二:
C
练习1
直线y=x+b与圆x2+y2=2相交时,b的取值范
围如何?
解:
圆心坐标为C(0,0),半径为
则圆心到直线的距离为
因为直线与圆相交,所以
即
解得:
还有有别的方法解答这个问题吗?
C
2、直线x-y-m=0与圆x2+y2=4相切时,m的取值范围如何?
分析:直线与圆相切,则圆心到直线的距离与圆的半径相等,即d=r。
参考答案:
练习
1
题型二
弦长问题
(
)
题型
三:直线和圆的相切问题
(
D
)
2.
总结:
判定直线
与圆的位置关系的方法有____种:
(2)代数法,由________________
的个数来判断;
(1)几何法,由_________________
______________的关系来判断。
在实际应用中,常采用第一种方法判定。
两
直线
与圆的公共点
圆心到直线的距离d
与半径r
4.2.1
直线与圆的位置关系
一、复习提问
1、点和圆的位置关系有几种?
(1)d
(2)d=r
点在圆上
(3)d>r
点
在圆外
结合图形,如何由数量关系判定直线与圆的位置关系?
当
时,直线与圆的位置关系是相离
当
时,直线与圆的位置关系是相切
当
时,直线与圆的位置关系是相交
d>r
d=r
d
2、直线和圆的位置关系有几种?
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法
d
>
r
d
=
r
d
<
r
直线与圆相离
直线与圆相切
直线与圆相交
(2).利用直线与圆的公共点的个数进行判断:
直线与圆相离
n=0
△<0
直线与圆相切
n=1
△=0
直线与圆相交
n=2
△>0
直线l:Ax+By+C=0,圆C:(x-a)2+(y-b)2=r2(r>0)
几何法
代数法
判断下列直线与圆的位置关系
相交
相切
相离
题型一:判断直线与圆的位置关系
解法一:
题型一:判断直线与圆的位置关系
解法二:
C
练习1
直线y=x+b与圆x2+y2=2相交时,b的取值范
围如何?
解:
圆心坐标为C(0,0),半径为
则圆心到直线的距离为
因为直线与圆相交,所以
即
解得:
还有有别的方法解答这个问题吗?
C
2、直线x-y-m=0与圆x2+y2=4相切时,m的取值范围如何?
分析:直线与圆相切,则圆心到直线的距离与圆的半径相等,即d=r。
参考答案:
练习
1
题型二
弦长问题
(
)
题型
三:直线和圆的相切问题
(
D
)
2.
总结:
判定直线
与圆的位置关系的方法有____种:
(2)代数法,由________________
的个数来判断;
(1)几何法,由_________________
______________的关系来判断。
在实际应用中,常采用第一种方法判定。
两
直线
与圆的公共点
圆心到直线的距离d
与半径r
