福建省福州市平潭县新世纪学校2020-2021学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 福建省福州市平潭县新世纪学校2020-2021学年高一下学期期中考试数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 446.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 00:00:00 | ||
图片预览




文档简介
平潭新世纪学校2020-2021学年高一下学期数学期中考试卷
一、单选题
1.已知复数false(false为虚数单位),则false( )
A.false B.2. C.false D.1
2.平行四边形ABCD中,false等于( )
A.false B.false C. D.false
3.已知向量false,若false,则实数false的值为( )
4551045129540A.2 B.false C.3 D.false
4.如图,已知等腰三角形false,false是一个平面图形的直观图,斜边false,则这个平面图形的面积是( )
A.false B.false C.false D.false
5.在平行四边形ABCD中,A(1,2),B(3,5),false=(-1,2),则false+false=( )
A.(-2,4) B.(4,6) C.(-6,-2) D.(-1,9)
6.若一个球的直径为2,则此球的表面积为( )
A.false B.false C.false D.false
7.已知向量false,向量false,则向量false在false方向上的投影为( )
A.1 B.-1 C.false D.false
8.已知false内角false,false,false所对的边分别为false,false,false,面积为false,若false,false,则false的形状是( )
A.等腰三角形 B.直角三角形 C.正三角形 D.等腰直角三角形
二、多选题
9.(多选)下列各组向量中,可以作为基底的是( )
A.false B.false C.false D.false
10.若四边形ABCD是矩形,则下列命题中正确的是( )
A.false共线 B.false相等 C.false模相等,方向相反 D.false模相等
11.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( )
A.64π cm2 B.36π cm2 C.54π cm2 D.48π cm2
12.设false的内角A,B,C的对边分别为a,b,c,若a=2,c=2false,cos A=false,则b=( )
A.2 B.3 C.4 D.false
第II卷(非选择题)
三、填空题
13.如图,在三角形ABC中,若D是边BC的中点,E是边AB上一点,则false_________.
14.false是虚数单位,复数false的共轭复数为______.
15.表面积为false的球,其内接正四棱柱(底面是正方形的直棱柱)的高是7,则这个正四棱柱的表面积为________.
16.给出下列命题:
①若false=false,则A、B、C、D四点是平行四边形的四个顶点; ②在false中,一定有false=false;
③若false,false,则false=false; ④若falsefalsefalse,falsefalsefalse,则falsefalsefalse.
其中所有正确命题的序号为________.
四、解答题
17.已知复数false,当实数false取什么值时,复数false是(1)零;(2)纯虚数.
18.计算:
(1)false; (2)false.
453326545339019.如图所示,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知false,false,试用false,false表示false,false.
20.已知false
(1)当false时,求x的值;
(2)当false时,求false.
21.已知false,false,false分别是false的三个内角false?false?false的对边,若false面积为false,false,false,求false,false及角false的值.
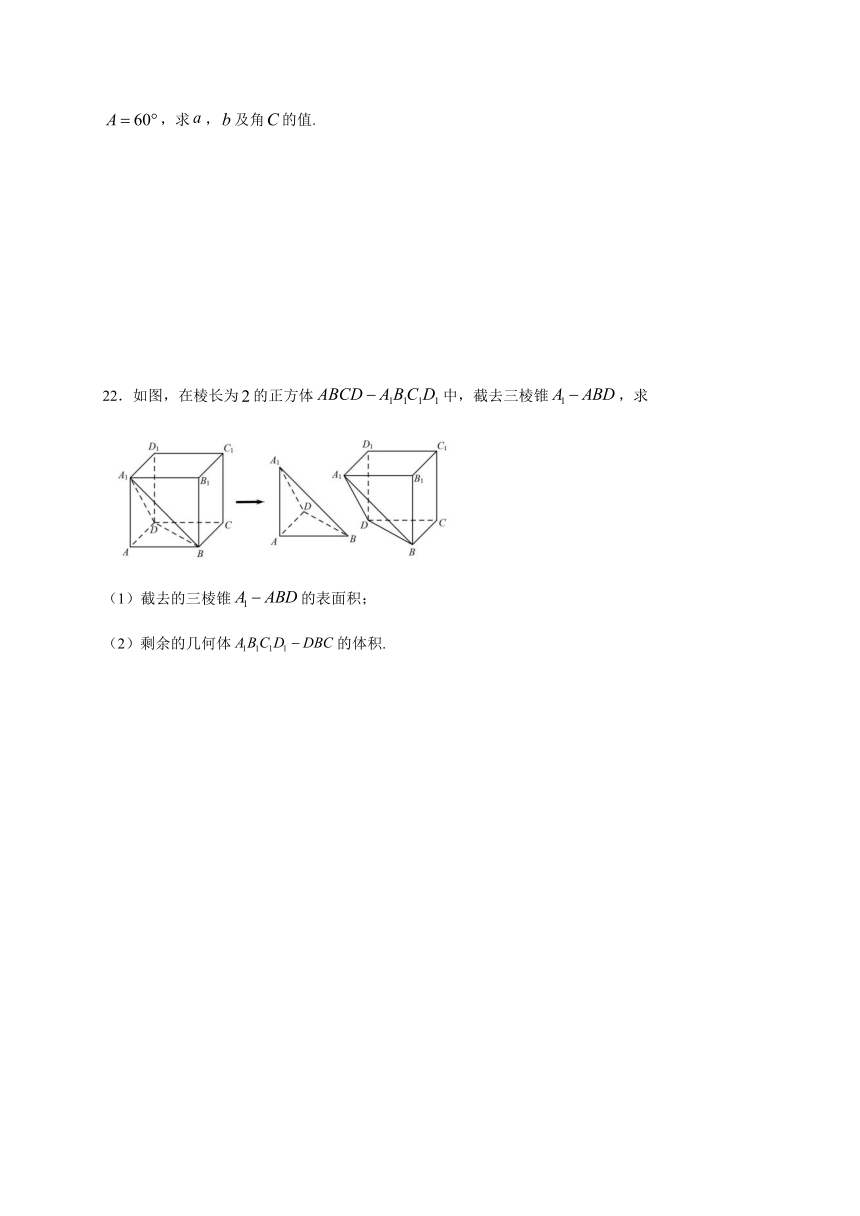
22.如图,在棱长为false的正方体false中,截去三棱锥false,求
(1)截去的三棱锥false的表面积;
(2)剩余的几何体false的体积.
参考答案
1.A
【分析】
首先根据两个复数代数形式的乘法运算法则,化简复数false,之后利用复数的模的运算公式求得结果.
【详解】
因为false,所以false.
故选:A.
2.B
【分析】
由平行四边形ABCD得,false,由此可得选项.
【详解】
在平行四边形ABCD中,false,所以false,
故选:B.
3.C
【分析】
直接由false可得解.
【详解】
向量false,
若false,则false,解得false.
故选:C.
4.D
【分析】
利用斜二测画法,由直观图作出原图三角形,再利用三角形面积公式即可求解.
【详解】
因为false是等腰直角三角形,false,所以false,
所以原平面图形为:
且false,false,false
所以原平面图形的面积是false,
故选:D
5.A
【分析】
利用平行四边形法则,结合向量坐标的加减运算,计算结果.
【详解】
在平行四边形ABCD中,因为A(1,2),B(3,5),所以false.又false,所以false,false,所以false.
故选:A.
6.D
【分析】
得出球的半径,直接由球的表面积公式即可得结果.
【详解】
因为球的直径为2,即球的半径为1,
所以球的表面积为false,
故选:D.
7.B
【分析】
根据向量false在false方向上的投影false,带入数值即可.
【详解】
向量false在false方向上的投影false.
故选:B
【点睛】
本题主要考查向量的投影,熟记公式是解决本题的关键,属于简单题.
8.C
【分析】
由false结合正弦定理、二倍角的正弦公式可求得false,由false结合三角形的面积公式,平面向量的数量积知识可得false,从而可得答案.
【详解】
因为false,所以false,
因为false,所以false,
所以false,
所以false,
因为false,所以false,所以false,
所以false,所以false,所以false,
因为false,所以false,
所以false,因为false,所以false,所以false,
所以false是正三角形.
故选:C
9.ABC
【分析】
平面向量中,不共线的两个向量可以作为一组基底.
【详解】
解:由两向量共线的坐标表示知,ABC中的向量均不共线.
对于D,false ,即false,所以共线.
故选: ABC
【点睛】
应用平面向量基本定理应注意:
①平面向量基本定理中的基底必须是两个不共线的向量;
②选定基底后,通过向量的加、减、数乘以及向量平行的充要条件,把相关向量用这一组基底表示出来;
③强调几何性质在向量运算中的作用,用基底表示未知向量,常借助图形的几何性质,如平行、相似等;④在基底未给出的情况下,合理地选取基底会给解题带来方便.
10.ACD
【分析】
根据向量的加法和减法的几何意义(平行四边形法则),结合矩形的判定与性质进行分析可解.
【详解】
∵四边形ABCD是矩形,false,
所以false共线,false模相等,故A、D正确;
∵矩形的对角线相等,∴|AC|=|BD|,
false模相等,但的方向不同,故B不正确;
|AD|=|CB|且AD∥CB,所以false的模相等,方向相反,
故C正确.
【点睛】
本题考查向量的共线,相等,模,向量的加减法的几何意义,属基础题,根据向量的加减法的平行四边形法则和矩形的性质综合判定是关键.
11.AB
【分析】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,根据圆的面积公式即可求解.
【详解】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,
即可得到两种不同大小的圆柱,其底面面积分别为64π cm2,36π cm2.
故选:AB
12.AC
【分析】
利用余弦定理即可求解.
【详解】
由余弦定理,
得a2=b2+c2-2bccos A,
∴4=b2+12-6b,
即b2-6b+8=0,
∴b=2或b=4.
故选:AC.
13.false
【分析】
利用平面向量的几何意义以及平面向量加法运算法则求解
【详解】
因为D是边BC的中点,
所以false
所以false
故答案为:false
14.false
【分析】
利用复数的除法化简复数false,利用共轭复数的定义可得出结果.
【详解】
false,因此,复数false的共轭复数为false.
故答案为:false.
15.144
【分析】
根据正四棱柱体的对角线长即为球的直径,建立方程求出四棱柱的底面边长,从而求出表面积
【详解】
false得false
设正四棱柱的底面正方形边长为false
正四棱柱体的对角线长即为球的直径
体对角线长为false
解得false
四棱柱的表面积为false
故答案为:144
16.②③
【分析】
对于①,由两向量共线可知A、B、C、D四点有可能在同一条直线上;对于②,由平行四边形的对边平行且相等可判断;对于③,由相等向量的定义判断即可;对于④,由于零向量与任何向量都共线,所以当false时,falsefalsefalse不一定成立
【详解】
解:false=false,A、B、C、D四点可能在同一条直线上,故①不正确;
在false中,false,false与false平行且方向相同,故false=false,故②正确;
false,则false,且false与false方向相同;false,则false,且false与false方向相同,则false与false长度相等且方向相同,故false=false,故③正确;
对于④,当false时,false与false不一定平行,故④不正确.
故答案为:②③
17.(1)false;(2)false.
【分析】
(1)根据复数false为零,得出false的实部和虚部均为零可得出关于实数false的方程组,进而可解得实数false的值;
(2)根据复数false为纯虚数可得出复数false的实部为零、虚部不为零可得出关于false的等式与不等式,由此可解得实数false的值.
【详解】
(1)因为false是零,所以false,解得false;
(2)因为false是纯虚数,所以false,解得false.
18.(1)false;(2)false.
【分析】
(1)根据向量的运算法则,展开整理,即可得答案.
(2)根据向量的运算法则,展开整理,即可得答案.
【详解】
(1)false
=false.
(2)false
=false
19.false,false.
【分析】
把MN放在△AMN中,把把MC放在△BMC中,利用向量加法的三角形法则.
【详解】
联结MN,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知false,
false;
false.
【点睛】
在几何图形中进行向量运算:
(1)构造向量加、减法的三角形法则和平行四边形法则;
(2)树立“基底”意识,利用基向量进行线性运算.
20.(1)false(2)false
【分析】
(1)根据共线向量的坐标公式,即可求解;
(2)由已知求出false,求出false的坐标,根据模长公式,即可求解.
【详解】
解:(1)由false,得false解得false
(2)当false时,有false,解得false
false,false
【点睛】
本题考查向量的坐标运算,涉及到共线向量、垂直、模长运算,属于基础题.
21.a=false;b=1;false
【分析】
由正弦定理的面积公式可先求出false,再结合余弦定理可求出false,再由正弦定理求出角false.
【详解】
false,所以false,所以b=1
false中,由余弦定理得a2=b2+c2-2bccosA=3,所以a=false,
由正弦定理false,即false,解得false,
所以false.
22.(1)false;(2)false
【分析】
(1)三棱锥false中false是边长为false的等边三角形,false、false、false都是直角边为false的等腰直角三角形,计算四个三角形面积之和即可求解.
(2)正方体的体积减去三棱锥false的体积即得剩余的几何体false的体积.
【详解】
(1)由正方体的特点可知三棱锥false中,false是边长为false的等边三角形,false、false、false都是直角边为false的等腰直角三角形,
所以截去的三棱锥false的表面积
false
(2)正方体的体积为false,
三棱锥false的体积为false,
所以剩余的几何体false的体积为false.
一、单选题
1.已知复数false(false为虚数单位),则false( )
A.false B.2. C.false D.1
2.平行四边形ABCD中,false等于( )
A.false B.false C. D.false
3.已知向量false,若false,则实数false的值为( )
4551045129540A.2 B.false C.3 D.false
4.如图,已知等腰三角形false,false是一个平面图形的直观图,斜边false,则这个平面图形的面积是( )
A.false B.false C.false D.false
5.在平行四边形ABCD中,A(1,2),B(3,5),false=(-1,2),则false+false=( )
A.(-2,4) B.(4,6) C.(-6,-2) D.(-1,9)
6.若一个球的直径为2,则此球的表面积为( )
A.false B.false C.false D.false
7.已知向量false,向量false,则向量false在false方向上的投影为( )
A.1 B.-1 C.false D.false
8.已知false内角false,false,false所对的边分别为false,false,false,面积为false,若false,false,则false的形状是( )
A.等腰三角形 B.直角三角形 C.正三角形 D.等腰直角三角形
二、多选题
9.(多选)下列各组向量中,可以作为基底的是( )
A.false B.false C.false D.false
10.若四边形ABCD是矩形,则下列命题中正确的是( )
A.false共线 B.false相等 C.false模相等,方向相反 D.false模相等
11.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( )
A.64π cm2 B.36π cm2 C.54π cm2 D.48π cm2
12.设false的内角A,B,C的对边分别为a,b,c,若a=2,c=2false,cos A=false,则b=( )
A.2 B.3 C.4 D.false
第II卷(非选择题)
三、填空题
13.如图,在三角形ABC中,若D是边BC的中点,E是边AB上一点,则false_________.
14.false是虚数单位,复数false的共轭复数为______.
15.表面积为false的球,其内接正四棱柱(底面是正方形的直棱柱)的高是7,则这个正四棱柱的表面积为________.
16.给出下列命题:
①若false=false,则A、B、C、D四点是平行四边形的四个顶点; ②在false中,一定有false=false;
③若false,false,则false=false; ④若falsefalsefalse,falsefalsefalse,则falsefalsefalse.
其中所有正确命题的序号为________.
四、解答题
17.已知复数false,当实数false取什么值时,复数false是(1)零;(2)纯虚数.
18.计算:
(1)false; (2)false.
453326545339019.如图所示,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知false,false,试用false,false表示false,false.
20.已知false
(1)当false时,求x的值;
(2)当false时,求false.
21.已知false,false,false分别是false的三个内角false?false?false的对边,若false面积为false,false,false,求false,false及角false的值.
22.如图,在棱长为false的正方体false中,截去三棱锥false,求
(1)截去的三棱锥false的表面积;
(2)剩余的几何体false的体积.
参考答案
1.A
【分析】
首先根据两个复数代数形式的乘法运算法则,化简复数false,之后利用复数的模的运算公式求得结果.
【详解】
因为false,所以false.
故选:A.
2.B
【分析】
由平行四边形ABCD得,false,由此可得选项.
【详解】
在平行四边形ABCD中,false,所以false,
故选:B.
3.C
【分析】
直接由false可得解.
【详解】
向量false,
若false,则false,解得false.
故选:C.
4.D
【分析】
利用斜二测画法,由直观图作出原图三角形,再利用三角形面积公式即可求解.
【详解】
因为false是等腰直角三角形,false,所以false,
所以原平面图形为:
且false,false,false
所以原平面图形的面积是false,
故选:D
5.A
【分析】
利用平行四边形法则,结合向量坐标的加减运算,计算结果.
【详解】
在平行四边形ABCD中,因为A(1,2),B(3,5),所以false.又false,所以false,false,所以false.
故选:A.
6.D
【分析】
得出球的半径,直接由球的表面积公式即可得结果.
【详解】
因为球的直径为2,即球的半径为1,
所以球的表面积为false,
故选:D.
7.B
【分析】
根据向量false在false方向上的投影false,带入数值即可.
【详解】
向量false在false方向上的投影false.
故选:B
【点睛】
本题主要考查向量的投影,熟记公式是解决本题的关键,属于简单题.
8.C
【分析】
由false结合正弦定理、二倍角的正弦公式可求得false,由false结合三角形的面积公式,平面向量的数量积知识可得false,从而可得答案.
【详解】
因为false,所以false,
因为false,所以false,
所以false,
所以false,
因为false,所以false,所以false,
所以false,所以false,所以false,
因为false,所以false,
所以false,因为false,所以false,所以false,
所以false是正三角形.
故选:C
9.ABC
【分析】
平面向量中,不共线的两个向量可以作为一组基底.
【详解】
解:由两向量共线的坐标表示知,ABC中的向量均不共线.
对于D,false ,即false,所以共线.
故选: ABC
【点睛】
应用平面向量基本定理应注意:
①平面向量基本定理中的基底必须是两个不共线的向量;
②选定基底后,通过向量的加、减、数乘以及向量平行的充要条件,把相关向量用这一组基底表示出来;
③强调几何性质在向量运算中的作用,用基底表示未知向量,常借助图形的几何性质,如平行、相似等;④在基底未给出的情况下,合理地选取基底会给解题带来方便.
10.ACD
【分析】
根据向量的加法和减法的几何意义(平行四边形法则),结合矩形的判定与性质进行分析可解.
【详解】
∵四边形ABCD是矩形,false,
所以false共线,false模相等,故A、D正确;
∵矩形的对角线相等,∴|AC|=|BD|,
false模相等,但的方向不同,故B不正确;
|AD|=|CB|且AD∥CB,所以false的模相等,方向相反,
故C正确.
【点睛】
本题考查向量的共线,相等,模,向量的加减法的几何意义,属基础题,根据向量的加减法的平行四边形法则和矩形的性质综合判定是关键.
11.AB
【分析】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,根据圆的面积公式即可求解.
【详解】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,
即可得到两种不同大小的圆柱,其底面面积分别为64π cm2,36π cm2.
故选:AB
12.AC
【分析】
利用余弦定理即可求解.
【详解】
由余弦定理,
得a2=b2+c2-2bccos A,
∴4=b2+12-6b,
即b2-6b+8=0,
∴b=2或b=4.
故选:AC.
13.false
【分析】
利用平面向量的几何意义以及平面向量加法运算法则求解
【详解】
因为D是边BC的中点,
所以false
所以false
故答案为:false
14.false
【分析】
利用复数的除法化简复数false,利用共轭复数的定义可得出结果.
【详解】
false,因此,复数false的共轭复数为false.
故答案为:false.
15.144
【分析】
根据正四棱柱体的对角线长即为球的直径,建立方程求出四棱柱的底面边长,从而求出表面积
【详解】
false得false
设正四棱柱的底面正方形边长为false
正四棱柱体的对角线长即为球的直径
体对角线长为false
解得false
四棱柱的表面积为false
故答案为:144
16.②③
【分析】
对于①,由两向量共线可知A、B、C、D四点有可能在同一条直线上;对于②,由平行四边形的对边平行且相等可判断;对于③,由相等向量的定义判断即可;对于④,由于零向量与任何向量都共线,所以当false时,falsefalsefalse不一定成立
【详解】
解:false=false,A、B、C、D四点可能在同一条直线上,故①不正确;
在false中,false,false与false平行且方向相同,故false=false,故②正确;
false,则false,且false与false方向相同;false,则false,且false与false方向相同,则false与false长度相等且方向相同,故false=false,故③正确;
对于④,当false时,false与false不一定平行,故④不正确.
故答案为:②③
17.(1)false;(2)false.
【分析】
(1)根据复数false为零,得出false的实部和虚部均为零可得出关于实数false的方程组,进而可解得实数false的值;
(2)根据复数false为纯虚数可得出复数false的实部为零、虚部不为零可得出关于false的等式与不等式,由此可解得实数false的值.
【详解】
(1)因为false是零,所以false,解得false;
(2)因为false是纯虚数,所以false,解得false.
18.(1)false;(2)false.
【分析】
(1)根据向量的运算法则,展开整理,即可得答案.
(2)根据向量的运算法则,展开整理,即可得答案.
【详解】
(1)false
=false.
(2)false
=false
19.false,false.
【分析】
把MN放在△AMN中,把把MC放在△BMC中,利用向量加法的三角形法则.
【详解】
联结MN,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知false,
false;
false.
【点睛】
在几何图形中进行向量运算:
(1)构造向量加、减法的三角形法则和平行四边形法则;
(2)树立“基底”意识,利用基向量进行线性运算.
20.(1)false(2)false
【分析】
(1)根据共线向量的坐标公式,即可求解;
(2)由已知求出false,求出false的坐标,根据模长公式,即可求解.
【详解】
解:(1)由false,得false解得false
(2)当false时,有false,解得false
false,false
【点睛】
本题考查向量的坐标运算,涉及到共线向量、垂直、模长运算,属于基础题.
21.a=false;b=1;false
【分析】
由正弦定理的面积公式可先求出false,再结合余弦定理可求出false,再由正弦定理求出角false.
【详解】
false,所以false,所以b=1
false中,由余弦定理得a2=b2+c2-2bccosA=3,所以a=false,
由正弦定理false,即false,解得false,
所以false.
22.(1)false;(2)false
【分析】
(1)三棱锥false中false是边长为false的等边三角形,false、false、false都是直角边为false的等腰直角三角形,计算四个三角形面积之和即可求解.
(2)正方体的体积减去三棱锥false的体积即得剩余的几何体false的体积.
【详解】
(1)由正方体的特点可知三棱锥false中,false是边长为false的等边三角形,false、false、false都是直角边为false的等腰直角三角形,
所以截去的三棱锥false的表面积
false
(2)正方体的体积为false,
三棱锥false的体积为false,
所以剩余的几何体false的体积为false.
同课章节目录
